Changing Perspectives in Mathematics Grades 4 to 6

Changing Perspectives in Mathematics Grades 4 to 6

Effective Teaching and Learning § Take a minute, reflect on your own experience learning mathematics. § How do you feel about mathematics? § If you had to use one word to describe mathematics, what would it be?

Goals for Mathematics Learning Students will § use mathematics confidently to solve problems § read, write, listen, and speak using mathematics language and symbols § develop a positive attitude toward mathematics § be confident in their ability to be successful in mathematics § appreciate and value the importance of mathematics in everyday life § use mathematics everyday

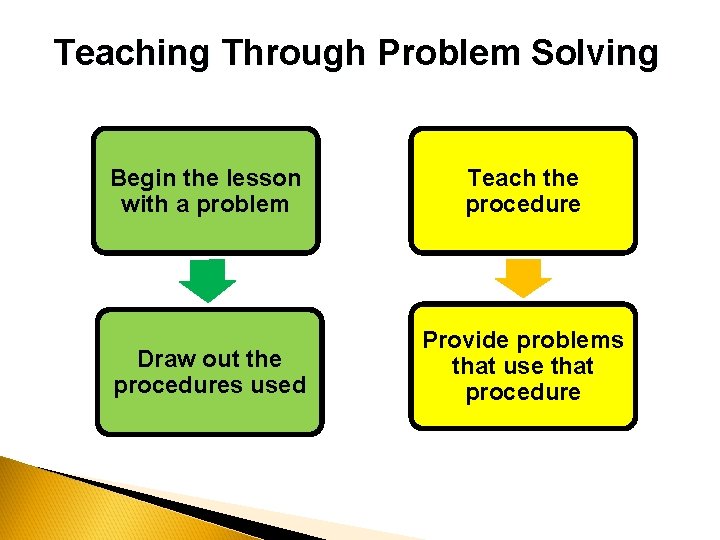
Teaching Through Problem Solving Begin the lesson with a problem Teach the procedure Draw out the procedures used Provide problems that use that procedure

Important Questions Why are we adopting this mathematics curriculum? What will my child be learning? Is this “new” mathematics? How will this change impact my child?

Why are we adopting this curriculum? § teacher feedback – time to teach and learn § parent feedback – students need to learn important topics to prepare them for life, future studies, and work § research over the last 10 years on how students learn mathematics and what topics are developmentally appropriate for students at a particular age § agreement that we need to focus on numeracy in early grades to build a solid foundation in mathematics § 21 st century expectations for learning, work, and life

What will my child be learning? Students will learn mathematics in five different areas that we call strands. The five strands are § Number (N) § Patterns and Relations (PR) § Measurement (M) § Geometry (G) § Statistics and Probability (SP)

Number (N)

Numbers Whole numbers § to 10 000 in grade 4 § to 1 000 in grade 5 § greater than 1 000 in grade 6 Decimal numbers § to hundredths in grade 4 § to thousandths in grade 5 § less than one-thousandth in grade 6 Fractions § proper fractions in grade 4 § equivalent fractions in grade 5 § improper fractions and mixed numbers in grade 6 § relating decimals and fractions in all three grades Ratio (grade 6) § part-to-part § part-to-whole § equivalent ratios Percent (grade 6) Integers (grade 6)

What will students learn about Number? To develop sound understanding of number, students will learn to § represent numbers in a variety of ways using concrete materials, pictures, money, words, expressions, and symbols § break numbers apart (partition) § estimate § compare and order numbers § recognize special numbers (prime and composite) § count money

Number Operations § Students will learn to solve addition, subtraction, multiplication, and division story problems (using numbers in context). § Students will quickly recall (in 3 -5 seconds) the basic facts o addition facts (grade 2) o subtraction facts (grade 3) o multiplication facts (grade 4) o division facts (grade 5) § Students will use mental mathematics to estimate sums, differences, products, and quotients and to calculate efficiently.

Number Operations § Students will use an efficient paper and pencil procedure to o add and subtract whole numbers (up to four-digits) and decimal numbers (up to thousandths) o multiply whole numbers (two- and three-digit by a one-digit multiplier, for example 345 x 3 and two-digit by a two-digit multiplier, for example 23 x 45) o multiply a decimal number by a whole number (one-digit whole number multiplier, for example 3. 67 x 2) o divide whole numbers (two- and three-digit by a one-digit divisor, for example 768÷ 5) o divide a decimal number by a whole number (one-digit whole number divisor, for example 7. 75 ÷ 5 )

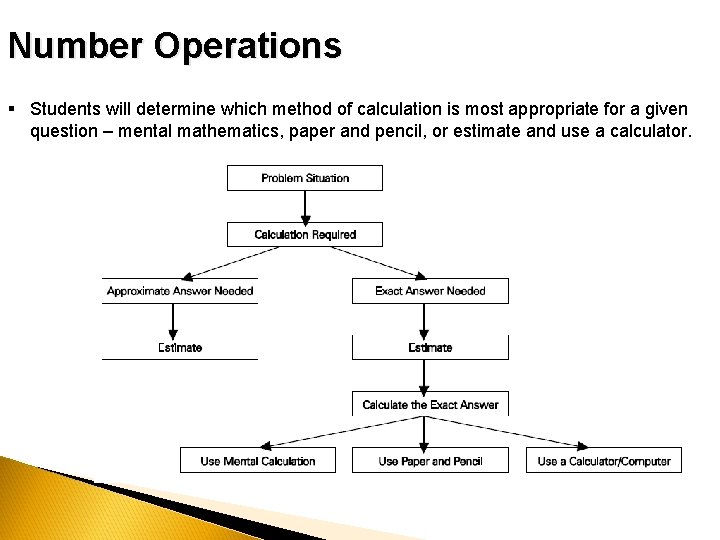
Number Operations § Students will determine which method of calculation is most appropriate for a given question – mental mathematics, paper and pencil, or estimate and use a calculator.

Mental Mathematics, Paper and Pencil, or Estimate and Use a Calculator? § 298 + 265 § 25 x 16 § 78 200 + 9900 § 2 x 12 x 50 § 13. 9 + 2. 5 § $9. 99 x 8 § 0. 2 + 0. 4 + 0. 8 + 0. 3 + 0. 6 § 62 x 4 § 5347 + 2432 § 456 x 159 § 33. 65 – 2. 99 § 482 ÷ 2 § 1. 6 – 0. 9 § 360 ÷ 3 § 64 000 – 13 900 § 545 ÷ 5 § 2. 53 – 1. 45 § 12 486 ÷ 23 § 45 678 – 21 543

Is this “new” math?

Fewer Topics, Greater Depth Students will be expected to § solve problems to learn mathematics § use concrete materials to model their thinking § draw pictures to show their thinking § talk about and explain their thinking § use symbols to record their thinking They will be completing active, hands-on and minds-on during mathematics learning tasks.

What does greater depth look like? For any given number, a student would be expected to § § § correctly read numerals without using the word “and” record numerals for numbers expressed orally, concretely, pictorially, or symbolically as expressions, using proper spacing without commas. describe the pattern of adjacent place positions moving from right to left explain the meaning of each digit in a given numeral. provide examples of large numbers used in print or electronic media. express a given numeral in expanded notation write the numeral represented by a given expanded notation compare and order numbers in a variety of ways represent a given numeral using a place-value chart. represent a given number in a variety of ways, and explain how they are equivalent represent a given number using expressions read and write given numerals, 0 to 1 000, in words

What does greater depth look like? § recording a number in standard form o 123 456 § recording a number as expressions o 100 000 + 23 000 + 400 + 56 o 123 000 + 456 o 124 000 - 544 § recording a number in expanded notation o 100 000 + 20 000 + 3000 + 400 + 50 + 6 § reading a number, such as 123 456, in a variety of ways o one hundred twenty three thousand four hundred fifty-six o 12 ten thousands, 3 thousands, forty-five tens, 6 ones o 123 thousands, 456 ones

What does greater depth look like? § representing numbers with base-ten blocks o 1 000 may be represented with a large cube that measures 1 m by 1 m o 100 000 may be represented with a large flat that measures 1 m by 10 cm o 10000 may be represented by a large rod that measures 1 m by 10 cm o 1000 may be represented by a cube that measures 10 cm by 10 cm o 100 may be represented by a flat that measures 10 cm by 1 cm o 10 may be represented by a rod that measures 10 cm by 1 cm o 1 may be represented by a small cube that measures 1 cm by 1 cm

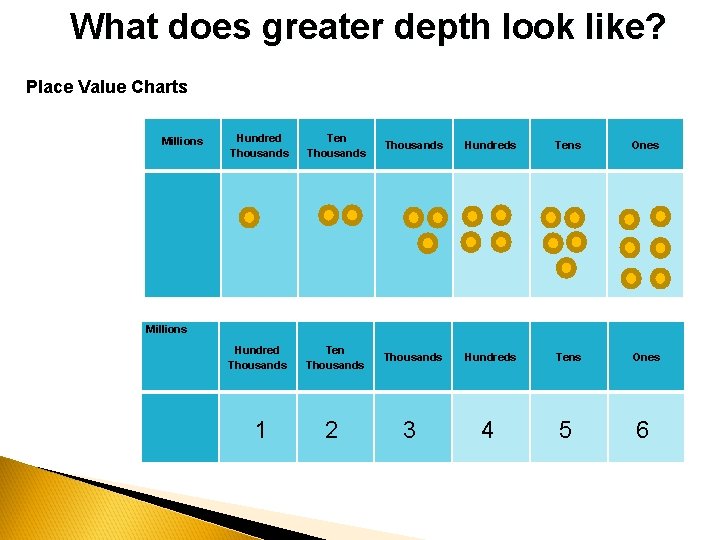
What does greater depth look like? Place Value Charts Millions Hundred Thousands Ten Thousands Hundreds Tens Ones 2 3 4 5 Millions 1 6

What does greater depth look like? § recording the number 123 456 when o it is expressed orally • I hear “one hundred twenty three thousand four hundred fifty-six” and I record 123 456 o it is represented with base-ten blocks • I am shown a picture of a large flat, two large rods, a three cubes, four flats, 5 rods, and 6 small cubes and I record 123 456 o it is represented in a place value chart with counters • I see a place value chart and I record 123 456 Millions Hundred Thousand s Ten Thousand s Hundreds Tens Ones

How will this impact my child?

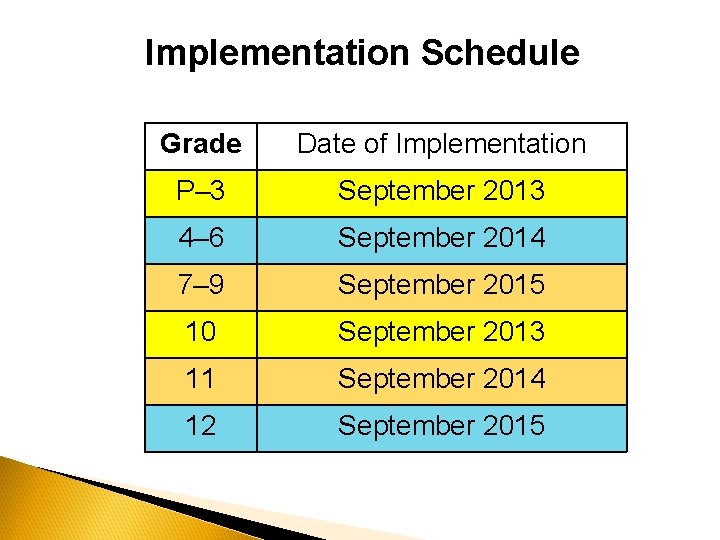
Implementation Schedule Grade Date of Implementation P– 3 September 2013 4– 6 September 2014 7– 9 September 2015 10 September 2013 11 September 2014 12 September 2015

§ Students entering Primary in September 2013 started school with the new curriculum. § Students entering grades 1 to 4 in 2014 will continue with the new curriculum. § Students who enter grade 5 and 6 in September 2014 have been well prepared for the new curriculum and a smooth transition to the new curriculum is expected.

How can I support my child’s learning in mathematics? § show a positive attitude and be enthusiastic about mathematics § talk to your child about his/her learning of mathematics § show confidence in your child’s ability to solve problems § encourage your child to “stick to it” when solving problems § celebrate success in mathematics learning § keep in touch with your child’s teacher

Mathematics is Everywhere! Provide opportunities for your child to use and to see you use mathematics at home. § talk about numbers and how you use mathematics in your daily life at work and at home § talk about money, budget, and the price of items that your family purchases § demonstrate how you comparison shop at the grocery store § show you use mathematics in activities that you like to do such as sewing, cooking, building, doing crafts, playing sports, gardening, playing music, or travelling § solve problems together § read books about mathematics § do puzzles of all kinds (jigsaw, hidden picture, matching)

Mathematics is Everywhere! Provide opportunities for your child to use and to see you use mathematics at home. § estimate and measure (height, mass, length, ingredients for a recipe, or produce in the grocery store) § read maps and talk about distance § talk about time, time management, schedules, and calendars § read the newspaper and discuss the graphs that are shown § play board games and logic games § look for and talk about patterns and shapes § use a recipe and cook together