CHAMELEON A Hierarchical Clustering Algorithm Using Dynamic Modeling

CHAMELEON: A Hierarchical Clustering Algorithm Using Dynamic Modeling Author: George et al. Advisor: Dr. Hsu Graduate: Zen. John Huang IDSL seminar 2001/10/23

Outline n Motivation n Objective n Research restrict n Literature review An overview of related clustering algorithms n The limitations of clustering algorithms n n CHAMELEON n Concluding remarks n Personal opinion

Motivation n Existing clustering algorithms can breakdown n Choice of parameters is incorrect n Model is not adequate to capture the characteristics of clusters n Diverse shapes, densities, and sizes

Objective n Presenting a novel hierarchical clustering algorithm – CHAMELEON n Facilitating discovery of natural and homogeneous n Being applicable to all types of data

Research Restrict n In this paper, authors ignored the issue of scaling to large data sets that cannot fit in the main memory

Literature Review n Clustering n An overview of related clustering algorithms n The limitations of the recently proposed state of the art clustering algorithms

Clustering n The intracluster similarity is maximized and the intercluster similarity is minimized [Jain and Dubes, 1988] n Serving as the foundation for data mining and analysis techniques

Clustering(cont’d) n Applications n Purchasing patterns n Categorization of documents on WWW [Boley, et al. , 1999] n Grouping of genes and proteins that have similar functionality[Harris, et al. , 1992] n Grouping if spatial locations prone to earth quakes[Byers and Adrian, 1998]

An Overview of Related Clustering Algorithms n Partitional techniques n Hierarchical techniques

Partitional Techniques n K means[Jain and Dubes, 1988]

Hierarchical Techniques n CURE [Guha, Rastogi and Shim, 1998] n ROCK [Guha, Rastogi and Shim, 1999]

Limitations of Existing Hierarchical Schemas n CURE n Fail to take into account special characteristics

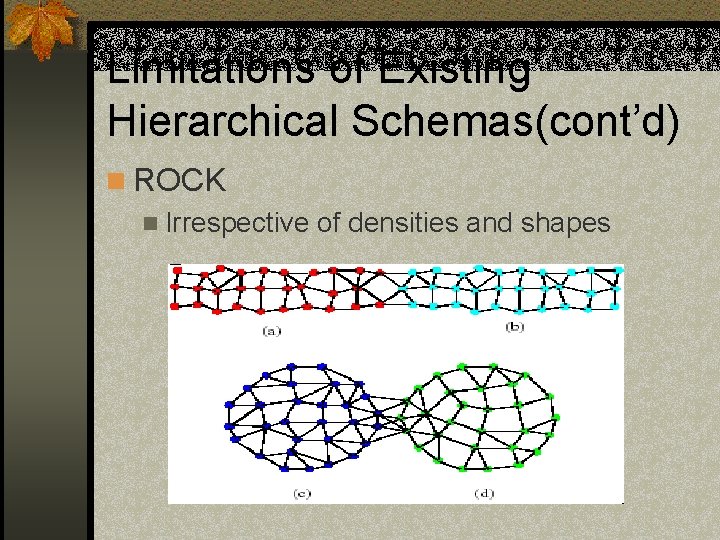
Limitations of Existing Hierarchical Schemas(cont’d) n ROCK n Irrespective of densities and shapes

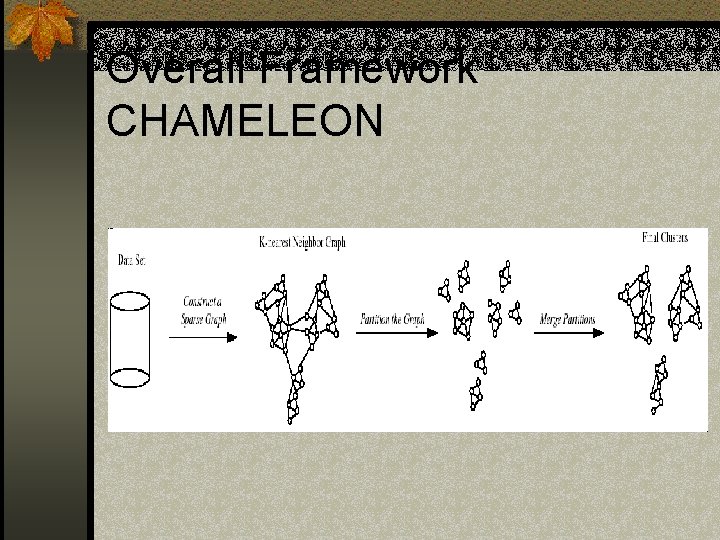
CHAMELEON n Overview n Modeling the data n Modeling the cluster similarity n A two-phase clustering algorithm n Performance analysis n Experimental Results

Overall Framework CHAMELEON

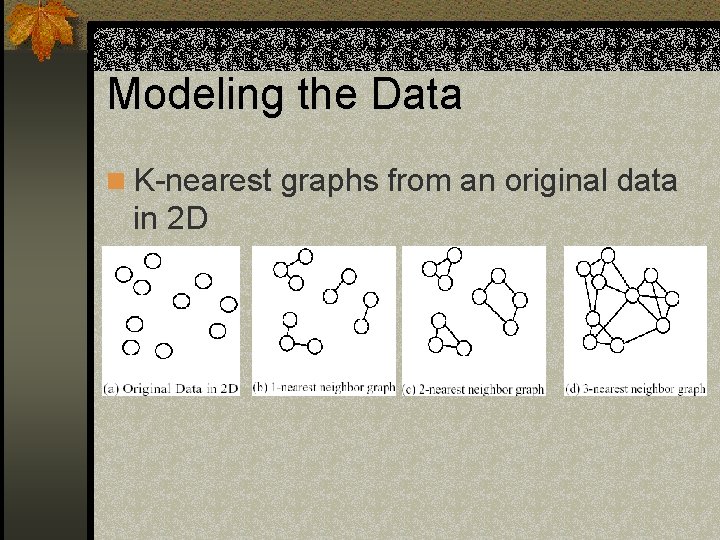
Modeling the Data n K-nearest graphs from an original data in 2 D

Modeling the Cluster Similarity n Relative inter-connectivity

Modeling the Cluster Similarity(cont’d) n Relative closeness

A Two-phase Clustering Algorithm n Phase I: Finding initial sub-clusters

A Two-phase Clustering Algorithm(cont’d) n Phase I: Finding initial sub-clusters n Multilevel paradigm[Karypis & Kumar, 1999] n h. Me. T|s [Karypis & Kumar, 1999]

A Two-phase Clustering Algorithm(cont’d) n Phase II: Merging sub-clusters using a dynamic framework TRI, TRC: user specified threshold

A Two-phase Clustering Algorithm(cont’d) n Phase II: Merging sub-clusters using a dynamic framework

Performance Analysis n The amount of time required to compute n K-nearest neighbor graph n Two-phase clustering

Performance Analysis(cont’d) n The amount of time required to compute n K-nearest neighbor graph n Low-dimensional data sets = O(n log n) n High-dimensional data sets = O(n 2)

Performance Analysis(cont’d) n The amount of time required to compute n Two-phase clustering n Computing internal inter-connectivity and closeness for each cluster: O(nm) n Selecting the most similar pair of cluster: O(n log n + m 2 log m) n Total time = O(nm + n log n + m 2 log m)

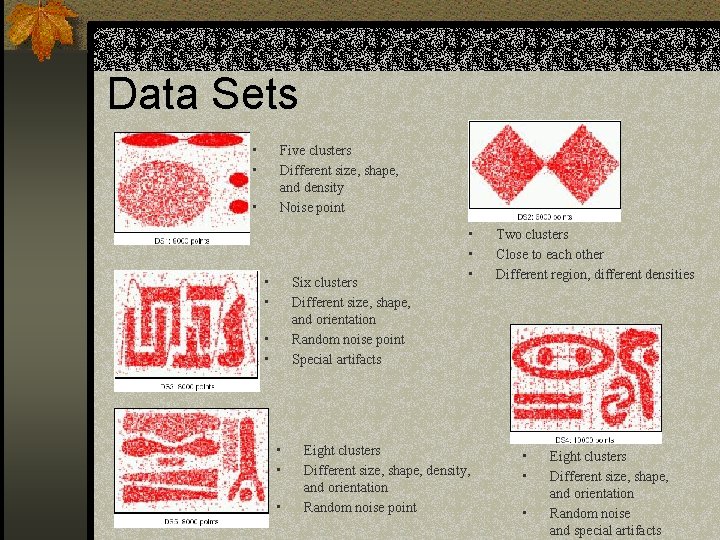
Experimental Results n Program n DBSCAN: a publicly available version n CURE: a locally implemented version n Data sets n Qualitative comparison

Data Sets • • Five clusters Different size, shape, and density Noise point • • • Six clusters Different size, shape, and orientation Random noise point Special artifacts • • Eight clusters Different size, shape, density, and orientation Random noise point Two clusters Close to each other Different region, different densities • • • Eight clusters Different size, shape, and orientation Random noise and special artifacts

Concluding remarks n CHAMELEON can discover natural clusters of different shapes and sizes n It is possible to use other algorithms instead of k-nearest neighbor graph n Different domains may require different models for capturing closeness and inter-connectivity

Personal Opinion n Without further work