Challenging Problem 2 1 Challenging problem 2 will

Challenging Problem 2: 1. Challenging problem 2 will be given on the website (week 4) at 9: 30 am on Saturday (Oct 1, 2005). 2. The due time is Sunday (Oct 2, 2005) at 12: 00 pm. 2/6/2022 chapter 25 1

Facts: • For each node in G, there are four 2 -paths that form 2 pairs of 2 -paths. • In an Euler circuit, one of the pairs is used. • A pair of 2 -path for v is good if the total cost of this pair of 2 -paths is not greater than that of the other pair. c a Pair 1: (a, c) and (b, d) b 2/6/2022 d Pair 2: (a, d) and (b, c) If c(a, c)=1, c(b, d)=1) c(a, d)=2 and c(b, d)=8, then pair 1 is good and pair 2 is bad. chapter 25 2

Algorithm: 1. 2. 3. 4. For each node v in G, fixed the good pair of 2 -path for v. (This leads to a set of edge disjoint cycles H. ) Constrruct a new (undirected) graph H’: Contract each circuit Ci in H into a single node ni. There is an edge(undirected) between ni and nj if Ci and Cj have a common vertex, say, v. The weight on edge (ni, nj) is w(e 1)+w(e 2)-w(e 3)-w(e 4), where e 1 and e 2 forms a bad pair for v, and e 3 and e 4 forms a good pair for v. Construct a minimum spanning tree for H’ Construct an Euler circuit for G by merging cycles based on the minimum spanning tree obtained in Step 3. 2/6/2022 chapter 25 3

Example: • Suppose that the directed Euler graph G is given in Figure 3(next page). There are 5 cycles. (a, b, c, d), (e, f, g, h), (i, j, k, l), (q, r, s, t), and (m, n, o, p). • The 2 -paths in the five cycles have cost 1 and the costs on other 2 -paths are listed below: w(a, e)=2, w(h, b)=2; w(f, i)=3, w(l, g)=3; w(g, t)=2, w(s, h)=11; w(k, m)=1, w(p, l)=2; w(t, o)=2, w(n, q)=3. 2/6/2022 chapter 25 4

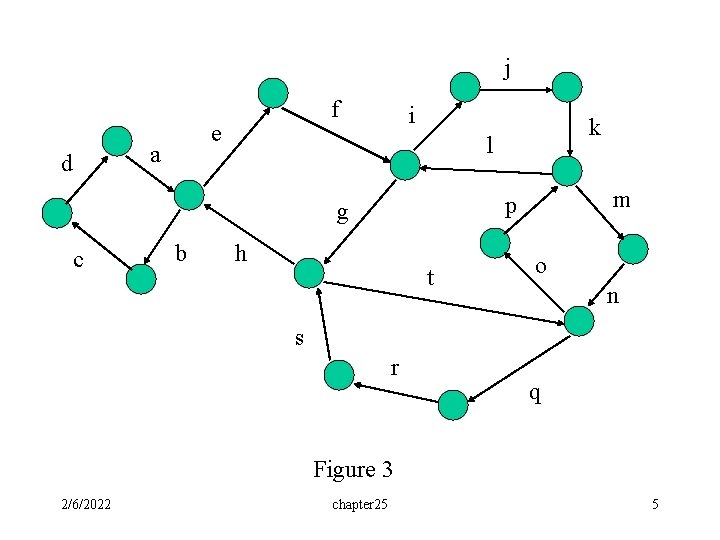
j d f e a i l b m p g c k h t o n s r q Figure 3 2/6/2022 chapter 25 5

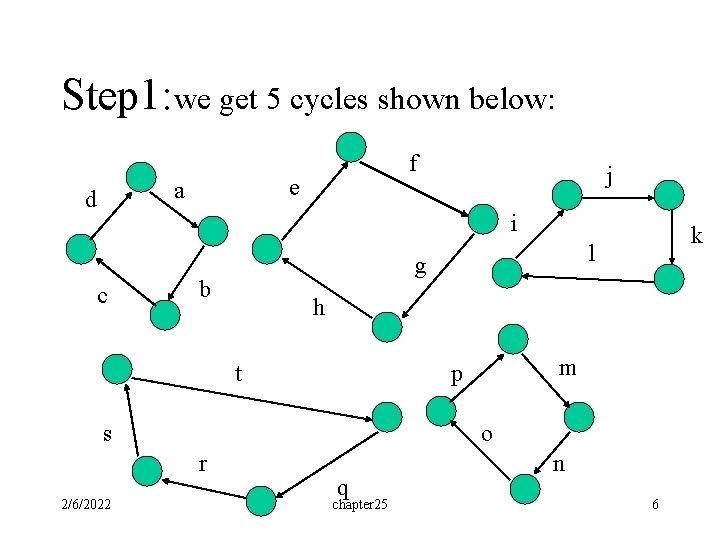
Step 1: we get 5 cycles shown below: e a d f j i c h t m p s o r 2/6/2022 l g b k q chapter 25 n 6

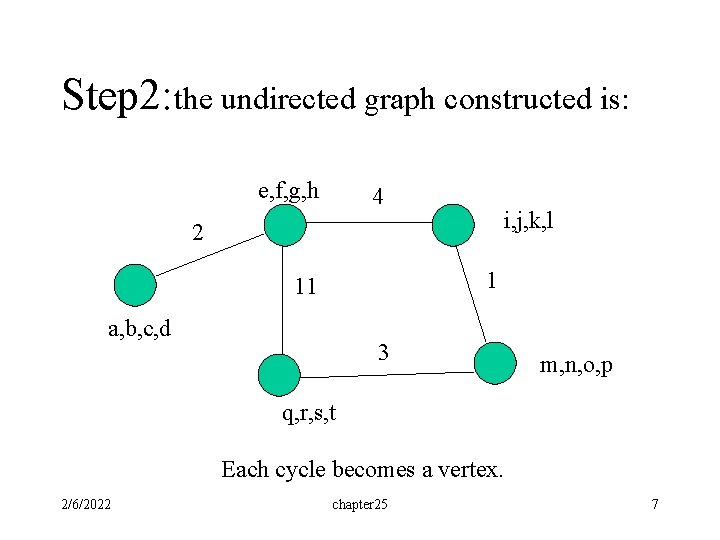
Step 2: the undirected graph constructed is: e, f, g, h 4 i, j, k, l 2 1 11 a, b, c, d 3 m, n, o, p q, r, s, t Each cycle becomes a vertex. 2/6/2022 chapter 25 7

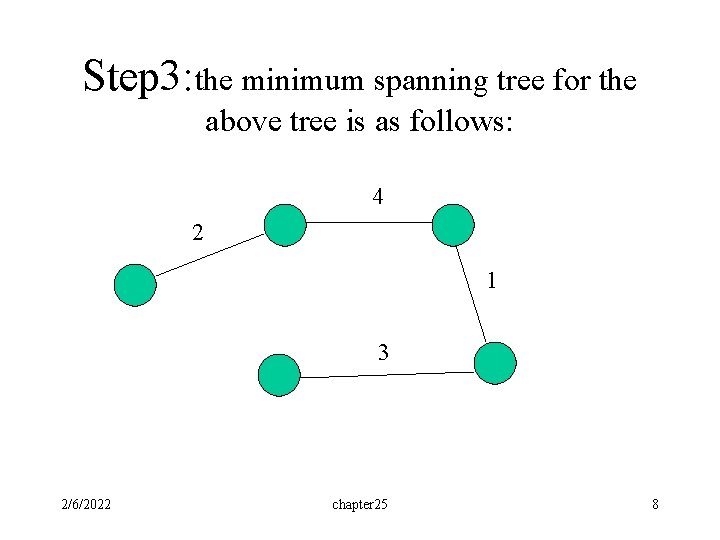
Step 3: the minimum spanning tree for the above tree is as follows: 4 2 1 3 2/6/2022 chapter 25 8

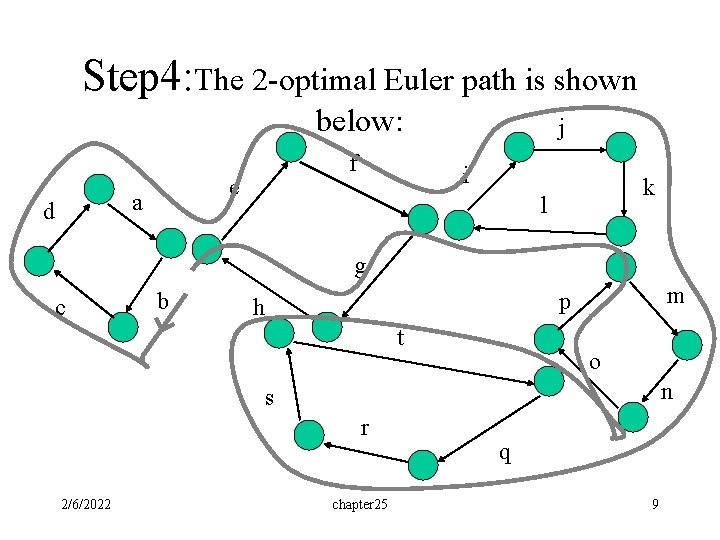
Step 4: The 2 -optimal Euler path is shown below: e a d f j i k l g c b m p h t o n s r 2/6/2022 chapter 25 q 9

Theorem: The above algorithm is correct. Explanation: • Let CC be the set of k cycles obtained in Steps 1. The total cost of the 2 -paths obtained in Step 1 is not greater than that of the optimal solution. • Let Copt be the optimal solution. Comparing Copt and CC, there are must be (at least) k-1 choices of pairs that are different and some k-1 different choices form a spanning tree in H’. • Those k-1 edges in the spanning tree correspond to (k-1) cycles merge operations. • The cost of Copt is the cost of CC + the cost of the spanning tree. • Since we use a minimum spanning tree, the cost of our solution is the smallest. 2/6/2022 chapter 25 10

Remarks about the Algorithm • The algorithm for 2 -optimal Euler circuit problem contains two phases. • Phase 1: always the good pair. • Phase: minimum spanning tree • Both phases use greedy strategies. 2/6/2022 chapter 25 11

Chapter 25 Single-Source Shortest Paths • Problem Definition • Shortest paths and Relaxation • Dijkstra’s algorithm (can be viewed as a greedy algorithm) 2/6/2022 chapter 25 12

Problem Definition: • Real problem: A motorist wishes to find the shortest possible route from Chicago to Boston. Given a road map of the United States on which the distance between each pair of adjacent intersections is marked, how can we determine this shortest route? • Formal definition: Given a graph G=(V, E, W), where each edge has a weight, find a shortest path from s to v for some interesting vertices s and v. • s—source • v—destination. 2/6/2022 chapter 25 13

Shortest path: • The weight of path p=<v 0, v 1, …, vk > is the sum of the weights of its constituent edges: The cost of the shortest path from s to v is denoted as (s, v). 2/6/2022 chapter 25 14

Negative-Weight edges: • Edge weight may be negative. • negative-weight cycles– the total weight in the cycle (circuit) is negative. • If no negative-weight cycles reachable from the source s, then for all v V, the shortest-path weight remains well defined, even if it has a negative value. • If there is a negative-weight cycle on some path from s to v, we define =-. 2/6/2022 chapter 25 15

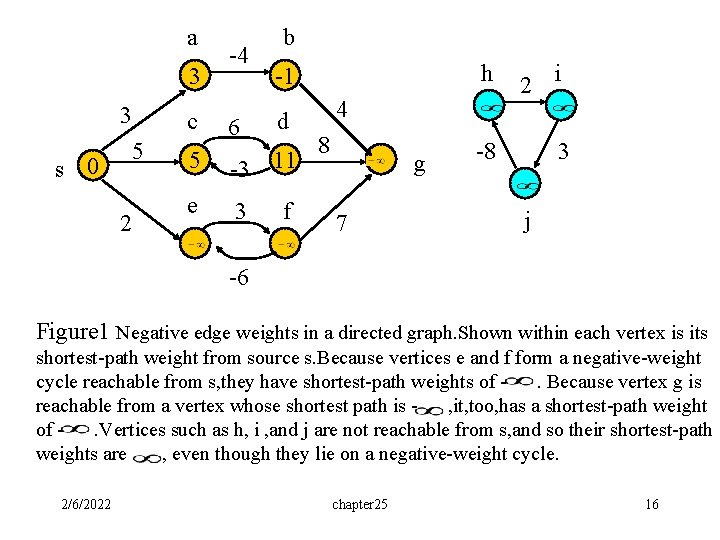
a 3 3 5 s 0 2 -4 b h -1 c d 6 5 -3 11 e 3 f 4 8 g 7 2 i -8 3 j -6 Figure 1 Negative edge weights in a directed graph. Shown within each vertex is its shortest-path weight from source s. Because vertices e and f form a negative-weight cycle reachable from s, they have shortest-path weights of. Because vertex g is reachable from a vertex whose shortest path is , it, too, has a shortest-path weight of. Vertices such as h, i , and j are not reachable from s, and so their shortest-path weights are , even though they lie on a negative-weight cycle. 2/6/2022 chapter 25 16

Representing shortest paths: • we maintain for each vertex v V , a predecessor [ v] that is the vertex in the shortest path right before v. • With the values of , a backtracking process can give the shortest path. (We will discuss that after the algorithm is given) 2/6/2022 chapter 25 17

• Observation: (basic) • Suppose that a shortest path p from a source s to a vertex v can be decomposed into s u v for some vertex u and path p’. Then, the weight of a shortest path from s to v is We do not know what is u for v, but we know u is in V and we can try all nodes in V in O(n) time. Also, if u does not exist, the edge (s, v) is the shortest. Question: how to find (s, u), the first shortest from s to some node? 2/6/2022 chapter 25 18

Relaxation: • The process of relaxing an edge (u, v) consists of testing whether we can improve the shortest path to v found so far by going through u and, if so, updating d[v] and [v]. • RELAX(u, v, w) • if d[v]>d[u]+w(u, v) • then d[v] d[u]+w(u, v) (based on obersation) • [v] u 2/6/2022 chapter 25 19

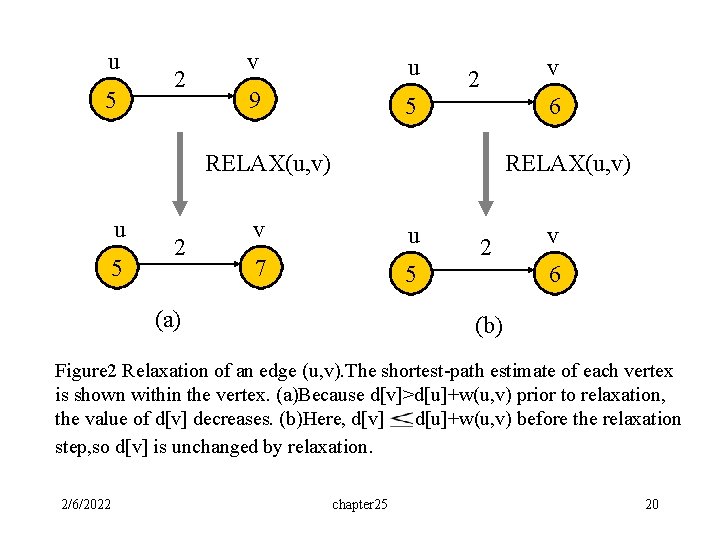
u 5 2 v u 9 5 v 2 6 RELAX(u, v) u 5 2 RELAX(u, v) v u 7 5 (a) 2 v 6 (b) Figure 2 Relaxation of an edge (u, v). The shortest-path estimate of each vertex is shown within the vertex. (a)Because d[v]>d[u]+w(u, v) prior to relaxation, the value of d[v] decreases. (b)Here, d[v] d[u]+w(u, v) before the relaxation step, so d[v] is unchanged by relaxation. 2/6/2022 chapter 25 20

Initialization: • For each vertex v V, d[v] denotes an upper bound on the weight of a shortest path from source s to v. • d[v]– will be (s, v) after the execution of the algorithm. • initialize d[v] and [v] as follows: . • INITIALIZE-SINGLE-SOURCE(G, s) • for each vertex v V[G] • do d[v] • [v] NIL • d[s] 0 2/6/2022 chapter 25 21

Dijkstra’s Algorithm: • Dijkstra’s algorithm assumes that w(e) 0 for each e in the graph. • maintain a set S of vertices such that – Every vertex v S, d[v]= (s, v), i. e. , the shortest-path from s to v has been found. (Intial values: S=empty, d[s]=0 and d[v]= ) • (a) select the vertex u V-S such that d[u]=min {d[x]|x V-S}. Set S=S {u} D[u]= (s, u) at this moment! Why? • (b) for each node v adjacent to u do RELAX(u, v, w). • Repeat step (a) and (b) until S=V. 2/6/2022 chapter 25 22

Continue: • • • DIJKSTRA(G, w, s): INITIALIZE-SINGLE-SOURCE(G, s) S Q V[G] while Q do u EXTRACT -MIN(Q) S S {u} for each vertex v Adj[u] do RELAX(u, v, w) 2/6/2022 chapter 25 23

Implementation: • a priority queue Q stores vertices in V-S, keyed by their d[] values. • the graph G is represented by adjacency lists. 2/6/2022 chapter 25 24

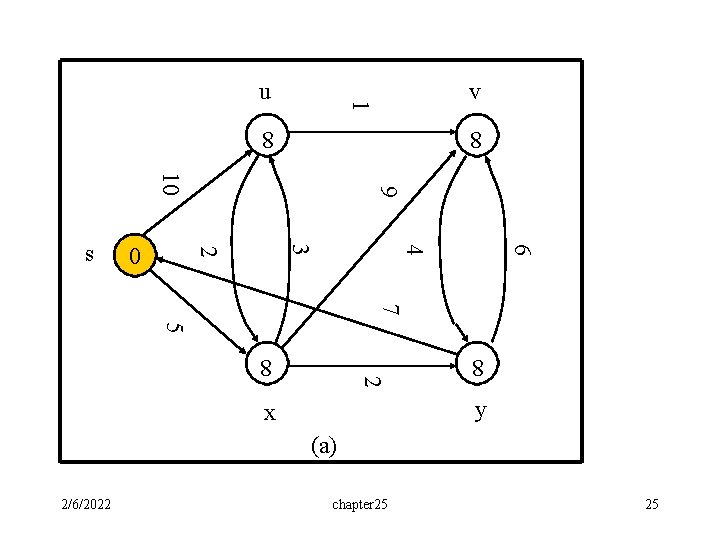
v 1 u 8 6 8 4 3 2 0 9 10 s 7 5 8 8 2 y x (a) 2/6/2022 chapter 25 25

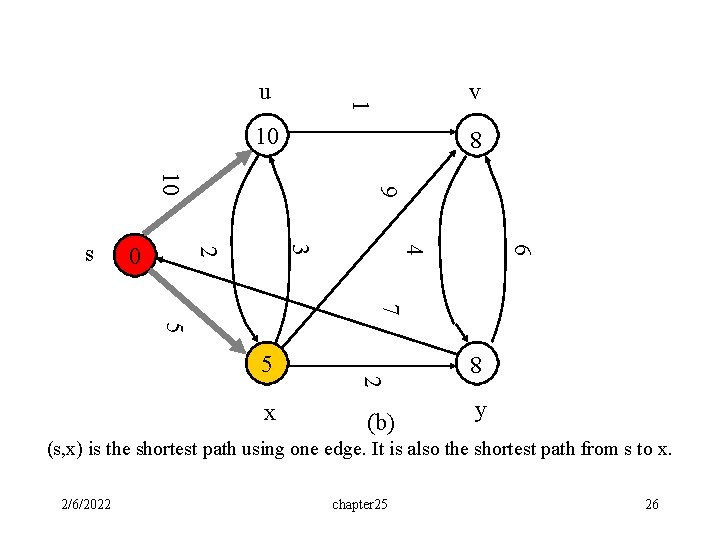
v 1 u 10 8 6 4 3 2 0 9 10 s 7 5 (b) 8 x 2 5 y (s, x) is the shortest path using one edge. It is also the shortest path from s to x. 2/6/2022 chapter 25 26

Assume EXTRACT -MIN(Q)=x. (s, x) is the shortest path using one edge. – Why? Since (s, x) is the shortest among all edges starting from s. • It is also the shortest path from s to x. Proof: (1) Suppose that path P: s->u…->x is the shortest path. Then w (s, u) w(s, x). (2) Since edges have non-negative weight, the total weight of path P is at least w(s, u) w(s, x). (3) So, the edge (s, x) is the shortest path from s to x. 2/6/2022 chapter 25 27

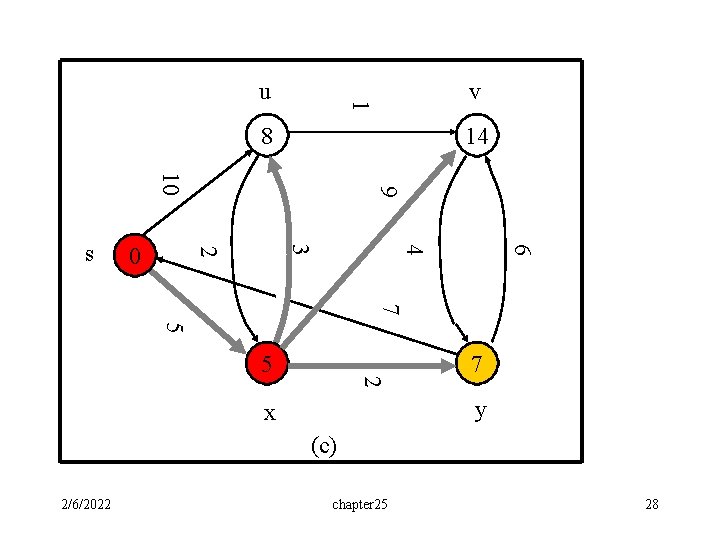
v 1 u 8 14 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (c) 2/6/2022 chapter 25 28

Statement: Suppose S={s, x} and d[y]=min d(v). ……(1) v V-S Then d[y] is the cost of the shortest, i. e. , either or (s->y) is the shortest path from s to y. s->x->y Why? If (s, y) is the shortest path, d[y] is correct. Consider that case: s->x->y is the shortest path for y. Proof by contradiction. Assume that s->x->y is not the shortest path and that P 1: s->yy->…->y is a shortest path and yy S. (At this moment, we already tried the case for yy=s and yy=x in the alg. ) Thus, w(P 1)< w(s->x->y). (from assumption: s->x-Y is not the shortest) Since w(e) 0 for any e, w(s->yy)<w(P 1)<w(s->x->y). Therefore, d[yy]<d[y] and (1) is not true. 2/6/2022 chapter 25 29

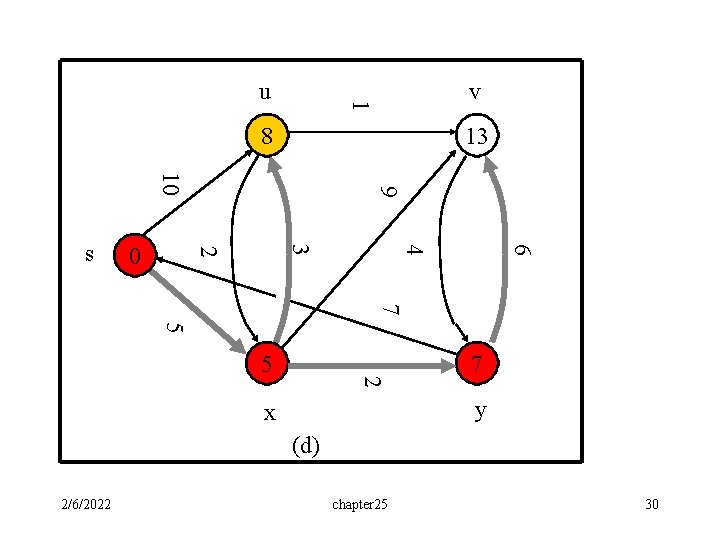
v 1 u 8 13 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (d) 2/6/2022 chapter 25 30

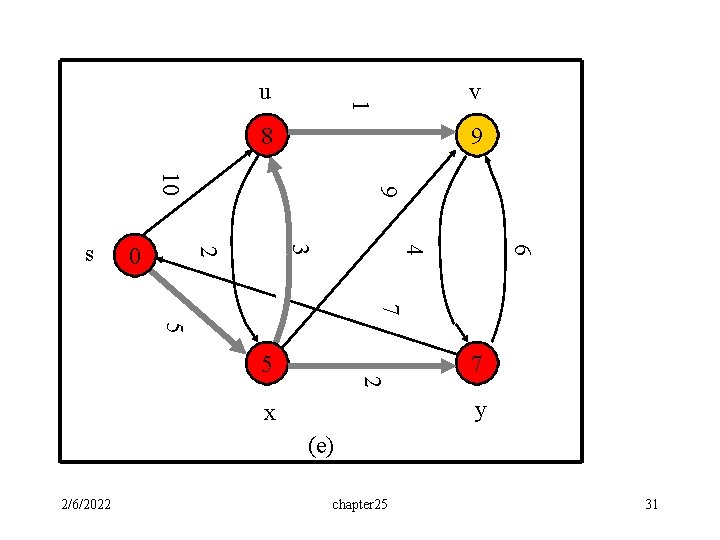
v 1 u 8 9 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (e) 2/6/2022 chapter 25 31

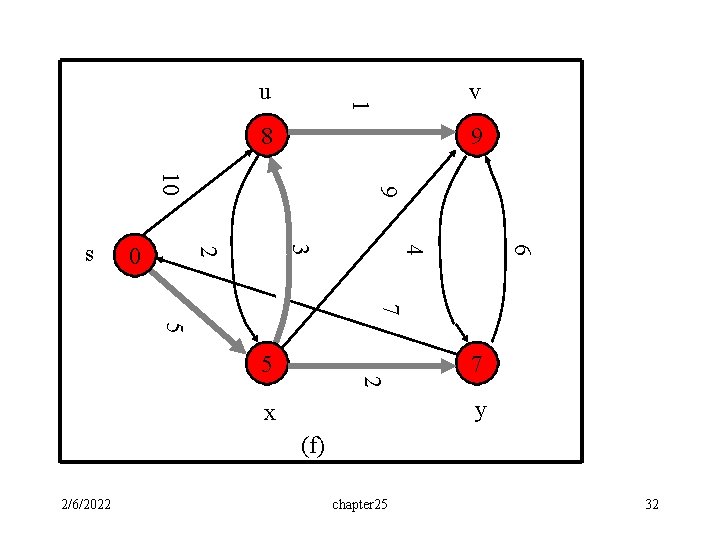
v 1 u 8 9 6 4 3 2 0 9 10 s 7 5 2 5 7 y x (f) 2/6/2022 chapter 25 32

Theorem: Let S be the set in algorithm and d[y]=min d(v). ……(1) v V-S Then d[y] is the cost of the shortest. (hard part) Proof: Assume that (1) for any v in S, y[v] is the cost of the shortest path. We want to show that d[y] is also the cost of the shortest path after execution of Step (a) Assume that (2) d[y] is NOT the cost of the shortest path from s to y and that P 1: s…->yy->…->y is a shortest path and yy S is the 1 st node in P 1 not in S. Thus, w(P 1)<d[y]. So, w(s…->yy)<w(P 1). (weight of edge >=0) Thus, w(s…->yy)<w(P 1)<d[y]. From (1) and (2), after execution of step (a) d[yy] w(s…->yy). Therefore, d[yy]<d[y] and (1) is not true. 2/6/2022 chapter 25 33

Time complexity of Dijkstra’s Algorithm: • Time complexity depends on implementation of the Queue. • Method 1: Use an array to story the Queue • EXTRACT -MIN(Q) --takes O(|V|) time. – Totally, there are |V| EXTRACT -MIN(Q)’s. – time for |V| EXTRACT -MIN(Q)’s is O(|V|2). • RELAX(u, v, w) --takes O(1) time. – Totally |E| RELAX(u, v, w)’s are required. – time for |E| RELAX(u, v, w)’s is O(|E|). • Total time required is O(|V|2+|E|)=O(|V|2) • Backtracking with [] gives the shortest path in inverse order. • Method 2: The priority queue is implemented as a Fibonacci heap. It takes O(log n) time to do EXTRACTMIN(Q). The total running time is O(nlog n+E). 2/6/2022 chapter 25 34