CH TIU CHT LNG Ch tiu cht lng











![MATLAB Hàm [K, P, e] = lqr (A, B, Q, R) giải bài toán MATLAB Hàm [K, P, e] = lqr (A, B, Q, R) giải bài toán](https://slidetodoc.com/presentation_image/2a9a691d665b6c4a715bd35b3b9875f7/image-16.jpg)
![MATLAB Điều kiện đầu là [5 0], điều khiển sao cho y 2 >> MATLAB Điều kiện đầu là [5 0], điều khiển sao cho y 2 >>](https://slidetodoc.com/presentation_image/2a9a691d665b6c4a715bd35b3b9875f7/image-17.jpg)




- Slides: 22

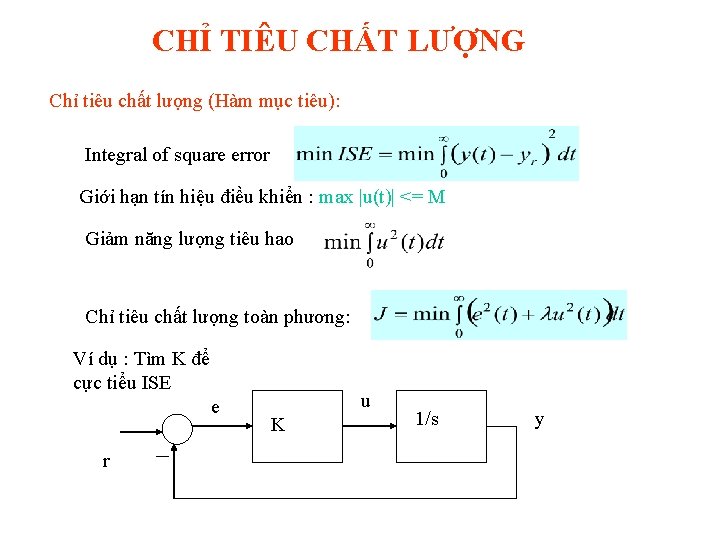
CHỈ TIÊU CHẤT LƯỢNG Chỉ tiêu chất lượng (Hàm mục tiêu): Integral of square error Giới hạn tín hiệu điều khiển : max |u(t)| <= M Giảm năng lượng tiêu hao Chỉ tiêu chất lượng toàn phương: Ví dụ : Tìm K để cực tiểu ISE e r u K 1/s y

TỐI ƯU THAM SỐ Hàm truyền sai số Với tín hiệu vào hàm nấc: e(t) = e - Kt Kết quả là K phải vô cùng Dùng chỉ tiêu J cực tiểu khi suy ra K = 1, J = 1

ĐIỀU CHỈNH TRẠNG THÁI (LQR) LINEAR QUADRATIC REGULATOR Khảo sát vấn đề duy trì trạng thái của hệ thống ở giá trị là 0, chống tác động nhiễu, đồng thời với cục tiểu tiêu hao năng lượng Q là ma trận đối xứng xđd hay bán xđd, thường là ma trận chéo R là ma trận đối xứng xđd, thường là ma trận chéo Chọn luật điều khiển hồi tiếp trạng thái u = - Kx, K là hằng số, thay vào biểu thức của J Tính K dùng phương trình Lyapunov, chọn hàm Lyapunov là J: V(x(0)) = J = x. T(0)Px(0) Đạo hàm theo thời gian

ĐIỀU CHỈNH TRẠNG THÁI Gỉa sử chọn K để hệ ổn định, x( ) 0 Mặt khác Suy ra Ma trận P thỏa phương trình Lyapunov

ĐIỀU CHỈNH TRẠNG THÁI Các bước giải bài toán tối ưu • Giải phương trình Lyapunov ta được các phần tử của ma trận P theo các phần tử của ma trận K chưa biết • Sau đó ta tính J = V(x(0)) = ma trận K • Để J cực tiểu ta giải phương trình • Suy ra ma trận K, luật điều khiển u = - Kx • Xét ổn định của ma trận A-BK • Nêú muốn điêù chỉnh ngõ ra y=cx ta chọn là hàm theo các phần tử của hay

PHƯƠNG TRÌNH ĐẠI SỐ RICCATI Đặt R = T , là ma trận vuông không suy biến Phương trình Lyapunov viết lại là: Lấy đạo hàm phương trình theo kij và dùng tính chất Ta suy ra Cực tiểu xảy ra khi số hạng trong ngoặc là 0 Phương trình Lyapunov trở thành phương trình đại số Riccati

VÍ DỤ 1 Các thông số của bài toán: A = -1, B = 1, Q = 2, R = 2 Phương trình Riccati ATP + PA - PBR-1 BTP + Q = 0 -P – P - 0. 5 P 2 + 2 = 0 Giải phương trình bậc hai theo P và chọn nghiệm dương Luật điều khiển tối ưu : Phương trình hệ kín:

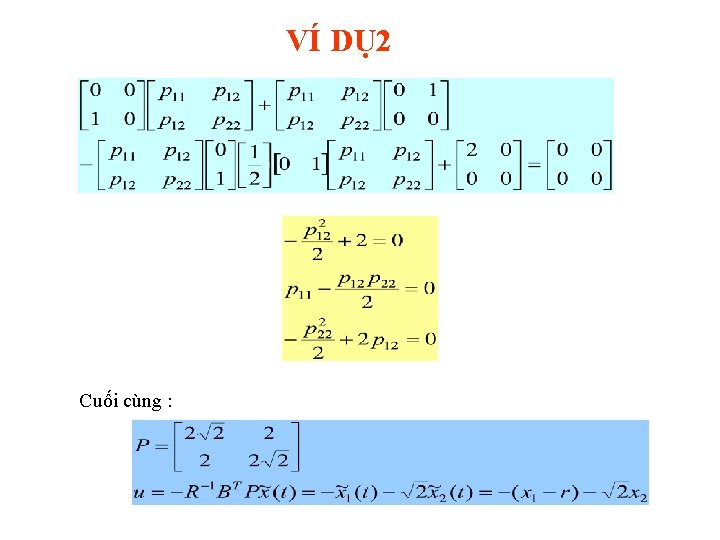
VÍ DỤ 2 Tìm luật điều khiển u duy trì x 1= r, x 2 = 0 u = - k 1(x 1 -r) - k 2 x 2 cực tiểu chỉ tiêu Đặt biến mới Phương trình Riccati: ATP + PA - PBR-1 BTP + Q = 0

VÍ DỤ 2 Cuối cùng :

VÍ DỤ 3 Điều khiển tối ưu với tích phân Trở lại ví dụ 1 ta muốn thêm vào khâu tích phân để tính chống nhiễu tốt hơn Đặt biến mới z(t)

VÍ DỤ 3 Điều khiển tối ưu với tích phân Phương trình Riccati Kết quả

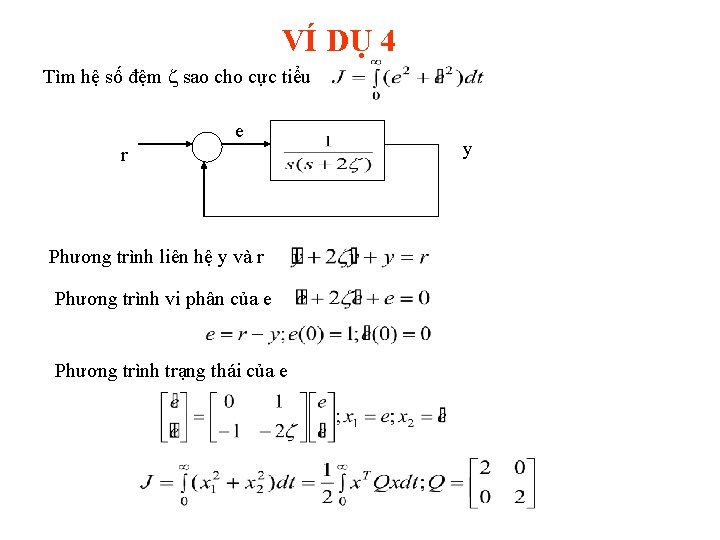
VÍ DỤ 4 Tìm hệ số đệm sao cho cực tiểu e r Phương trình liên hệ y và r Phương trình vi phân của e Phương trình trạng thái của e y

VÍ DỤ 4 Phương trình Riccati: ATP + PA + Q = 0 Giải pt Đạo hàm theo suy ra trị tối ưu ứng với

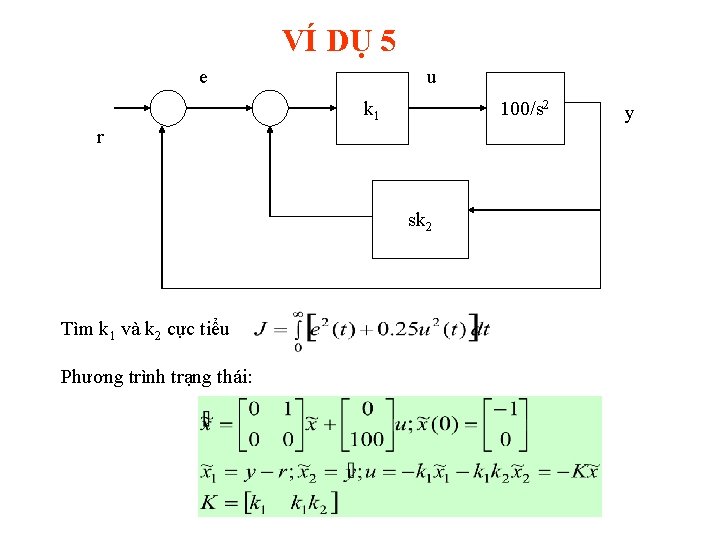
VÍ DỤ 5 e u k 1 100/s 2 r sk 2 Tìm k 1 và k 2 cực tiểu Phương trình trạng thái: y

VÍ DỤ 5 GiảI phương trình Riccati
![MATLAB Hàm K P e lqr A B Q R giải bài toán MATLAB Hàm [K, P, e] = lqr (A, B, Q, R) giải bài toán](https://slidetodoc.com/presentation_image/2a9a691d665b6c4a715bd35b3b9875f7/image-16.jpg)
MATLAB Hàm [K, P, e] = lqr (A, B, Q, R) giải bài toán cực tiểu Phương trình Riccati ATP + PA - PBR-1 BTP + Q = 0 u = -Kx e là nghiệm riêng của ma trận A-BK Ví dụ 4: Lấy lại ví dụ 2 k= 1. 0000 >> A = [0 1; 0 0]; >> B = [0; 1]; >> C = [1 0]; >> Q = [2 0; 0 0]; >> R = [2]; >> [k , p, e] = lqr (A, B, Q, R) 1. 4142 p= 2. 8284 2. 0000 2. 8284 e= -0. 7071 + 0. 7071 i -0. 7071 - 0. 7071 i
![MATLAB Điều kiện đầu là 5 0 điều khiển sao cho y 2 MATLAB Điều kiện đầu là [5 0], điều khiển sao cho y 2 >>](https://slidetodoc.com/presentation_image/2a9a691d665b6c4a715bd35b3b9875f7/image-17.jpg)
MATLAB Điều kiện đầu là [5 0], điều khiển sao cho y 2 >> ptttk = ss (A - B*k, B*k(1, 1), C, 0) >> t = 0: 0. 1: 10; >> r = 2*ones (size(t)); >> [y, t, x] = lsim (ptttk, r, t, [5 0]); >> plot (t, y) >> hold on >> u = -k*x' + k (1, 1) *r; >> plot(t, u) Điều kiện đầu là [5 0], điều khiển sao cho y 0 >> ptttk = ss (A - B*k, [0; 0], C, 0) >> [y, t, x] = lsim (ptttk, r, t, [5 0]); >> plot (t, y) >> hold on >> u = -k*x‘; >> plot (t, u)

ĐIỀU KHIỂN TỐI ƯU HỆ RỜI RẠC Phương trình Riccati rời rạc Dùng Matlab [K, P, e] = dlqr (F, G, Q, R)

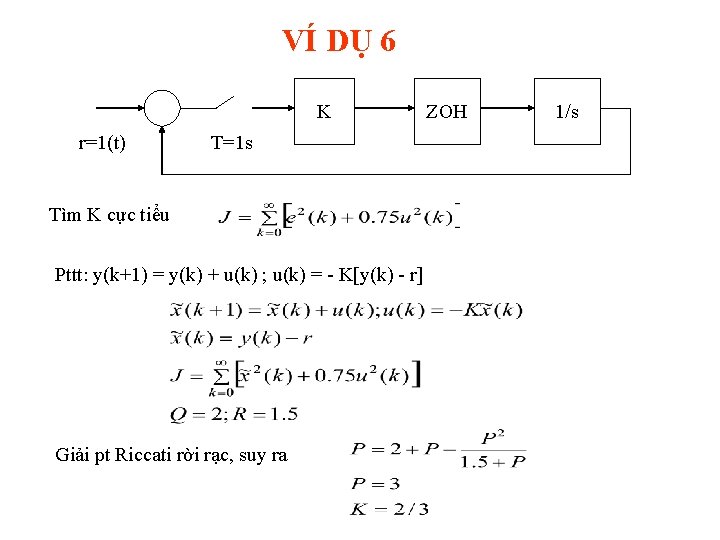
VÍ DỤ 6 K r=1(t) T=1 s Tìm K cực tiểu Pttt: y(k+1) = y(k) + u(k) ; u(k) = - K[y(k) - r] Giải pt Riccati rời rạc, suy ra ZOH 1/s

VÍ DỤ 7 • Điêù khiển đối tượng 1/(s+1) với tín hiệu đặt yr = hằng số, cực tiểu G(z)=0. 632/(z-0. 368) y(k+1)=0. 368 y(k)+0. 632 u(k) F=0. 368, G=0. 632, Q=1, R=1 Phương trình Riccati: P=Q+FTPF-FTPG (R+GTPG) -1 GTPF =1+0. 135 P-0. 054 P 2/(1+0. 4 P) P=1. 11 K= (R+GTPG) -1 GTPF=0. 18 1/N=-C(F-GK-1) -1 G N=1. 18

VÍ DỤ 8 • Điêù khiển con lắc ngược, vơí pttt tuyến tính hóa Tính luật điều khiền trạng thái vớí khâu tích phân, cực tiểu

• • • • • • clear all close all A=[0, 1, 0, 0; 4. 4537, 0, 0, 0; 0, 0, 0, 1; -0. 5809, 0, 0, 0]; b=[0; -0. 3947; 0; 0. 9211]; c=[0, 0, 1, 0]; sys=ss(A, b, c, 0); T=0. 1 sysd=c 2 d(sys, T); [F, g, c, d]=ssdata(sysd); FI=[F(1, : ) , 0; F(2, : ) , 0; F(3, : ) , 0; F(4, : ) , 0; c*F, 1]; g. I=[g(1); g(2); g(3); g(4); c*g]; c. I=[c, 0]; U=ctrb(FI, g. I); rank. U=rank(U) Q=[10, 0, 0; 0, 1, 0, 0, 0; 0, 0, 100, 0, 0; 0, 0, 0, 1, 0; 0, 0, 1]; R=1; K=dlqr(FI, g. I, Q, R); Kp=[K(1), K(2), K(3), K(4)] Ki=K(5) FI_cl=FI-g. I*K; syscl=ss(FI_cl, [0; 0; -1], c. I, 0, T); t=[0: 0. 1: 20]; [y, t, X]=step(syscl, t); plot(t, y); grid; hold on; plot(t, X)