Ch 8 STRATEGY FOR INTEGRATION integration is more

Ch 8: STRATEGY FOR INTEGRATION integration is more challenging than differentiation. No hard and fast rules can be given as to which method applies in a given situation, but we give some advice on strategy that you may find useful. how to attack a given integral, you might try the following four-step strategy.

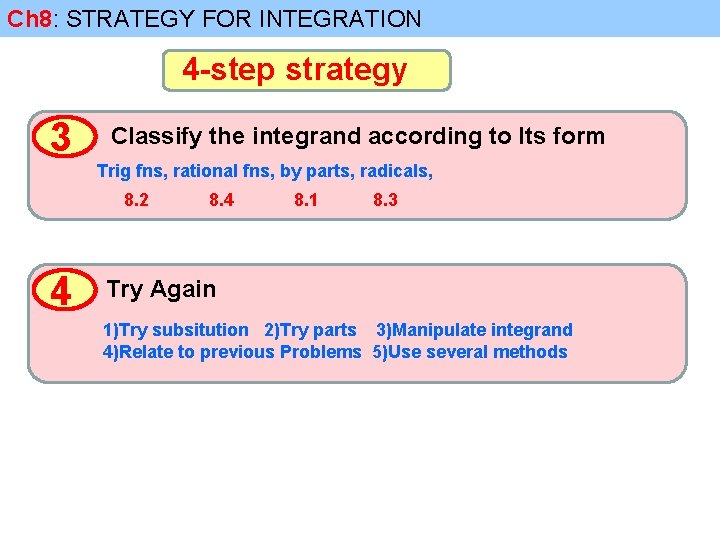
Ch 8: STRATEGY FOR INTEGRATION 4 -step strategy 1 Simplify the Integrand if Possible 2 Look for an Obvious Substitution function and its derivative 3 Classify the Integrand According to Its Form Trig fns, rational fns, by parts, radicals, 4 Try Again 1)Try subsitution 2)Try parts 3)Manipulate integrand 4)Relate to previous Problems 5)Use several methods

Ch 8: STRATEGY FOR INTEGRATION 4 -step strategy 1 Simplify the Integrand if Possible

Ch 8: STRATEGY FOR INTEGRATION 4 -step strategy 2 Look for an Obvious Substitution function and its derivative

Ch 8: STRATEGY FOR INTEGRATION 4 -step strategy 3 Classify the integrand according to Its form Trig fns, rational fns, by parts, radicals, 8. 2 4 8. 1 8. 3 Try Again 1)Try subsitution 2)Try parts 3)Manipulate integrand 4)Relate to previous Problems 5)Use several methods

Ch 8: STRATEGY FOR INTEGRATION

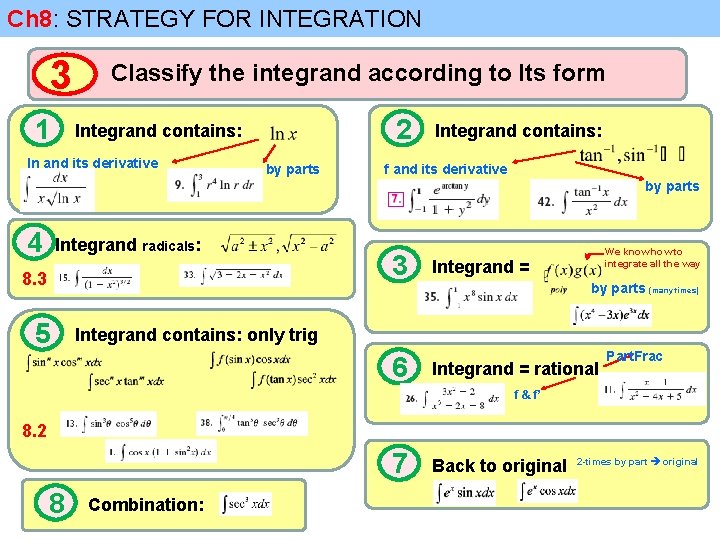
Ch 8: STRATEGY FOR INTEGRATION 3 1 Classify the integrand according to Its form 2 Integrand contains: ln and its derivative by parts Integrand contains: f and its derivative by parts 4 Integrand radicals: 8. 3 5 We know how to integrate all the way 3 Integrand = 6 Integrand = rational by parts (many times) Integrand contains: only trig Part. Frac f & f’ 8. 2 7 8 Combination: Back to original 2 -times by part original

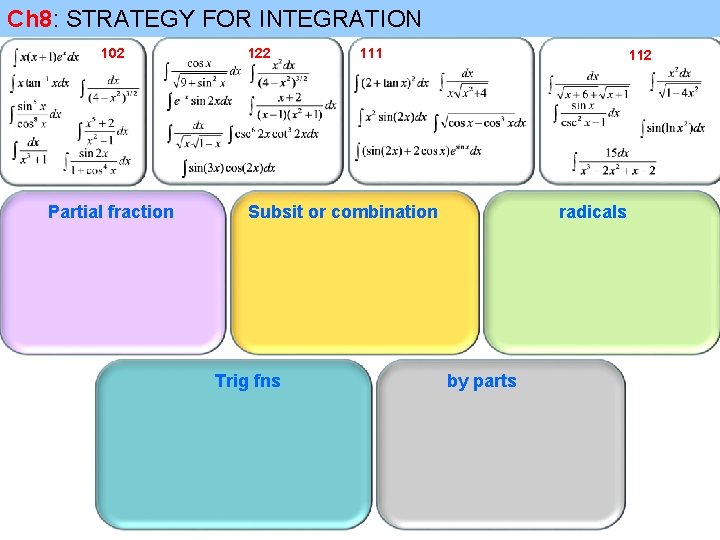
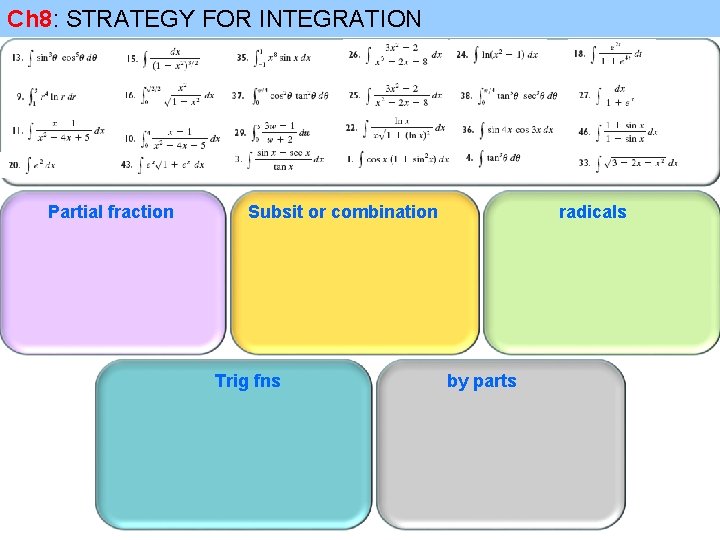
Ch 8: STRATEGY FOR INTEGRATION 102 Partial fraction 122 111 112 Subsit or combination Trig fns radicals by parts

Ch 8: STRATEGY FOR INTEGRATION 102 Partial fraction 122 111 112 Subsit or combination Trig fns radicals by parts

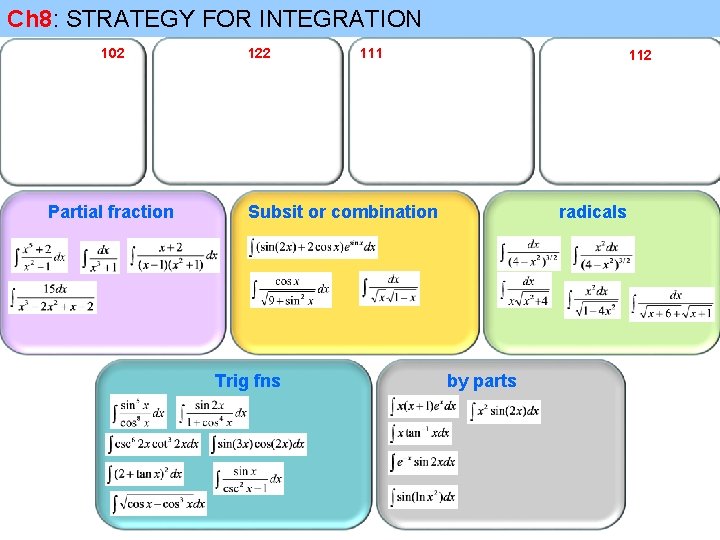
Ch 8: STRATEGY FOR INTEGRATION Partial fraction Subsit or combination Trig fns radicals by parts

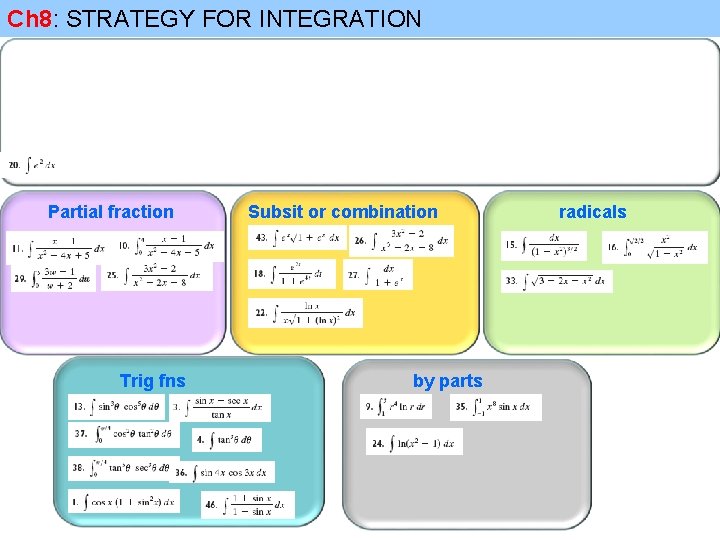
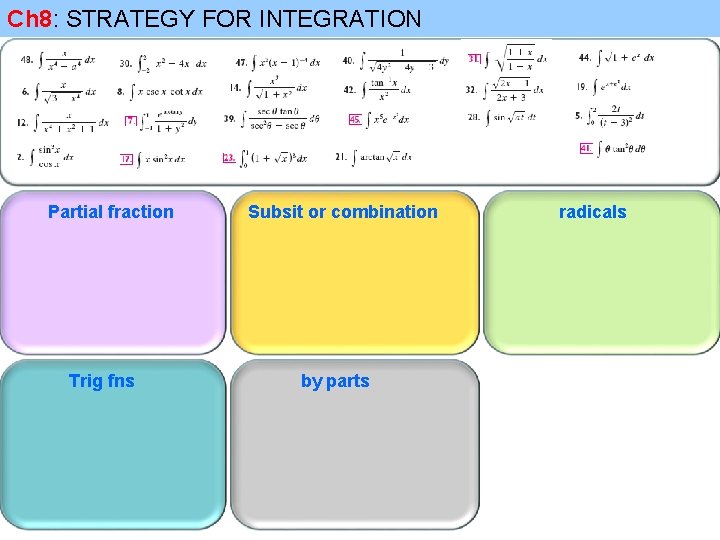
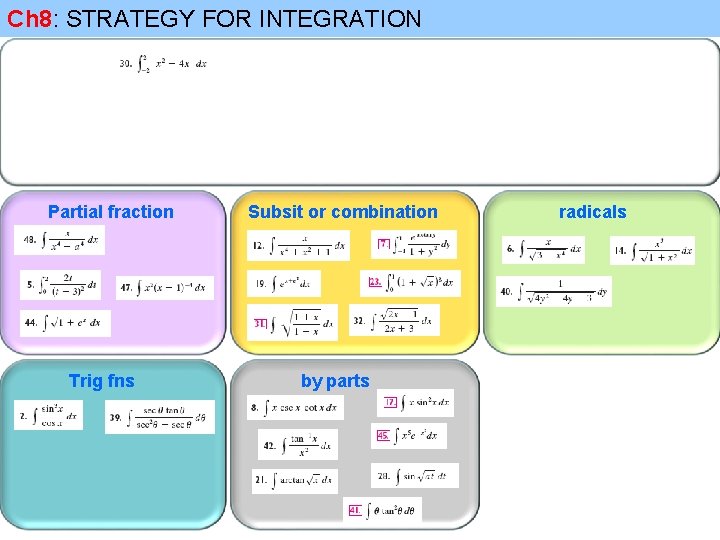
Ch 8: STRATEGY FOR INTEGRATION Partial fraction Trig fns Subsit or combination by parts radicals

Ch 8: STRATEGY FOR INTEGRATION Partial fraction Trig fns Subsit or combination by parts (Substitution then combination) radicals

Ch 8: STRATEGY FOR INTEGRATION Partial fraction Trig fns Subsit or combination by parts (Substitution then combination) radicals

Ch 8: STRATEGY FOR INTEGRATION CAN WE INTEGRATE ALL CONTINUOUS FUNCTIONS? if YES or NO Continuous. Will our strategy for integration enable us to find the integral of every continuous function? Anti-derivative YES or NO exist?

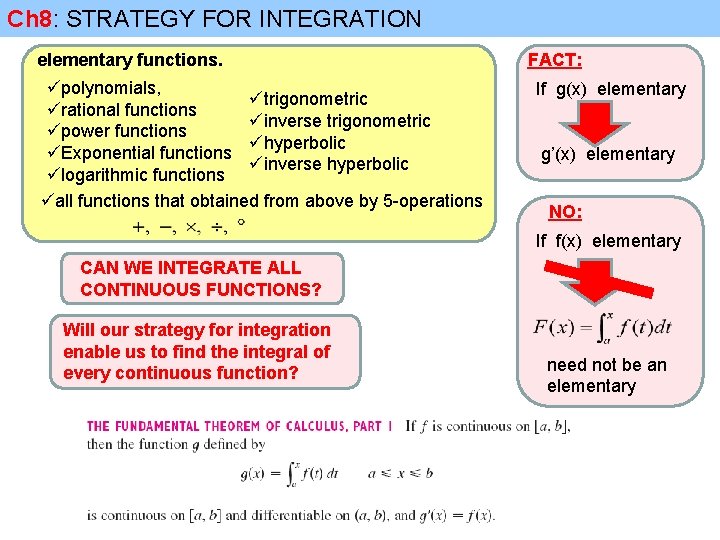
Ch 8: STRATEGY FOR INTEGRATION elementary functions. üpolynomials, ütrigonometric ürational functions üinverse trigonometric üpower functions ühyperbolic üExponential functions üinverse hyperbolic ülogarithmic functions üall functions that obtained from above by 5 -operations CAN WE INTEGRATE ALL CONTINUOUS FUNCTIONS? Will our strategy for integration enable us to find the integral of every continuous function? NO YES

Ch 8: STRATEGY FOR INTEGRATION elementary functions. üpolynomials, ütrigonometric ürational functions üinverse trigonometric üpower functions ühyperbolic üExponential functions üinverse hyperbolic ülogarithmic functions üall functions that obtained from above by 5 -operations FACT: If g(x) elementary g’(x) elementary NO: If f(x) elementary CAN WE INTEGRATE ALL CONTINUOUS FUNCTIONS? Will our strategy for integration enable us to find the integral of every continuous function? need not be an elementary

Ch 8: STRATEGY FOR INTEGRATION CAN WE INTEGRATE ALL CONTINUOUS FUNCTIONS? Will our strategy for integration enable us to find the integral of every continuous function? FACT: NO: If g(x) elementary If f(x) elementary g’(x) elementary need not be an elementary has an antiderivative is not an elementary. This means that no matter how hard we try, we will never succeed in evaluating in terms of the functions we know. In fact, the majority of elementary functions don’t have elementary antiderivatives.