Ch 7 Building Phylogenetic Tree Two general approaches

Ch 7 Building Phylogenetic Tree Two general approaches: (1) Distance methods: to find a tree that accounts for estimated evolutionary distances (2) Parsimony: to find a tree that requires minimum number of changes to explain the data Chapter 8 formulates phylogeny probabilistically: maximal likeliehood 1

7. 2 Background on trees • Distance of sequence: represented by edge length • Rooted tree: with information or conjecture about the location of the root, an ultimate ancestor • Unrooted tree: no such information – parsimony 2

n leaves: 2 n-1 nodes, 2 n-2 edges n leaves: 2 n-2 nodes, 2 n-3 edges From unrooted tree to rooted tree: a root can be added at any edge. So for n leaves, there are (2 n-3) times as many rooted trees as unrooted trees. 3

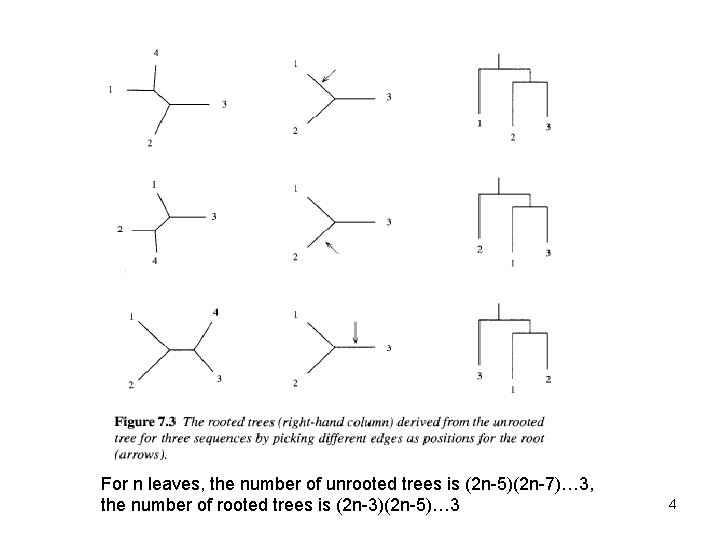
For n leaves, the number of unrooted trees is (2 n-5)(2 n-7)… 3, the number of rooted trees is (2 n-3)(2 n-5)… 3 4

5

7. 3 Making a tree from pairwise distances An example distance between sequences i and j: the fraction of sites u where residues xui and xuj differ UPGMA: Unweighted Pair Group Method using Arithmetic averages 6

7

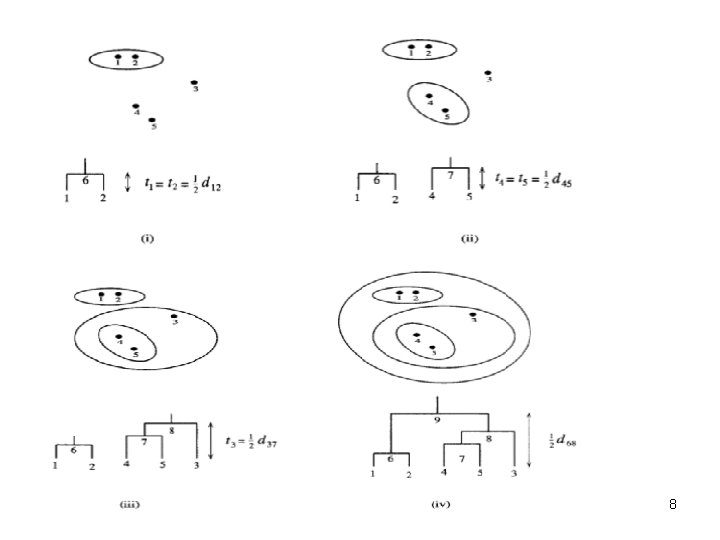
8

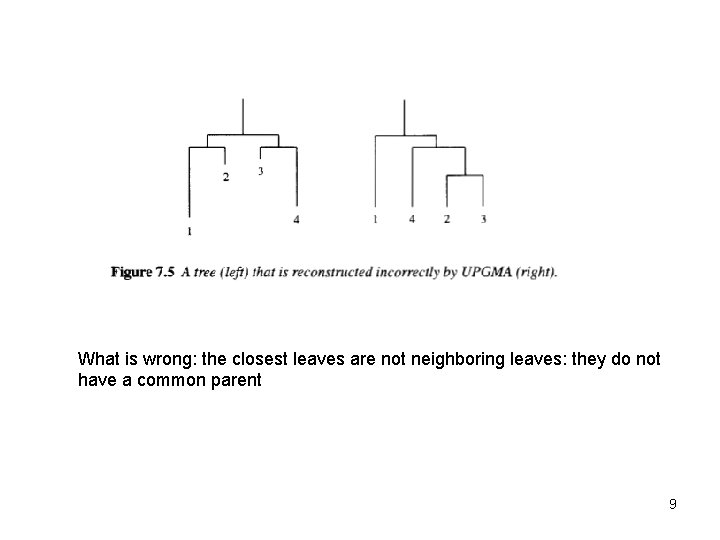
What is wrong: the closest leaves are not neighboring leaves: they do not have a common parent 9

10

11

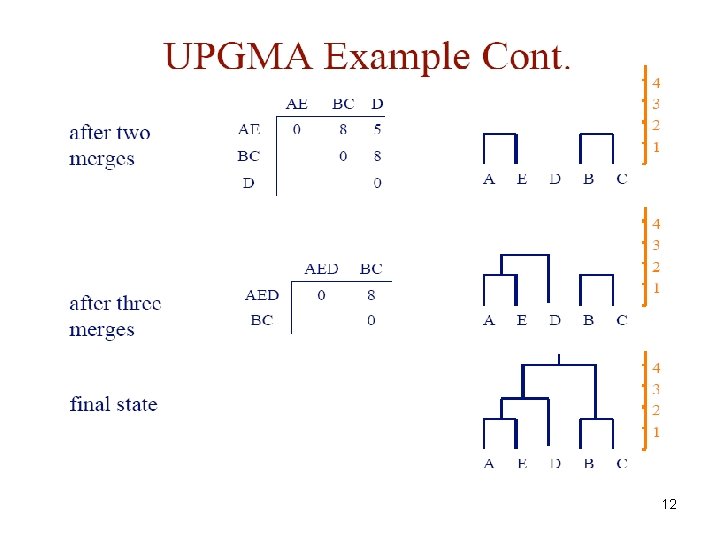
12

13

14

15

16

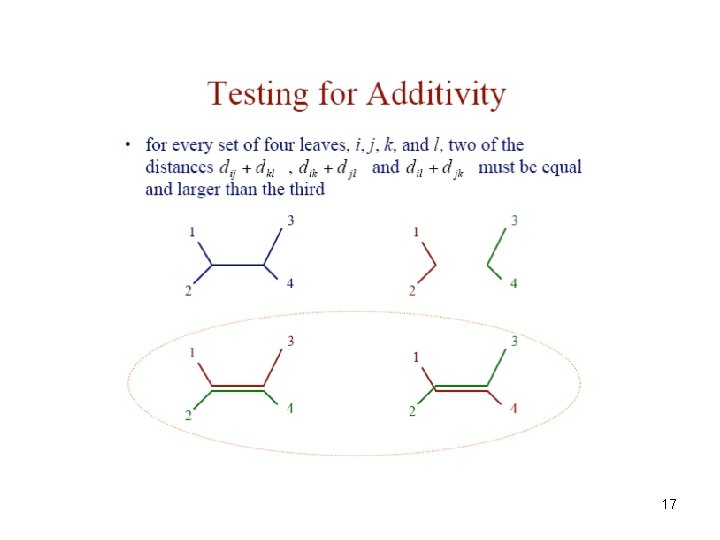
17

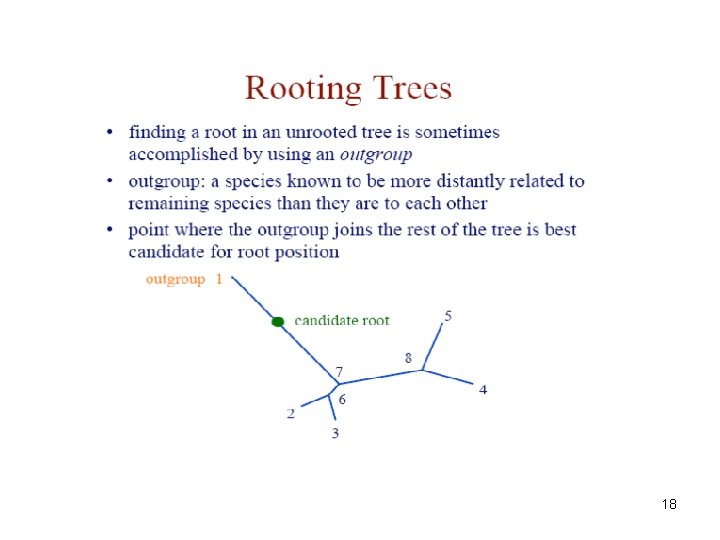
18

19

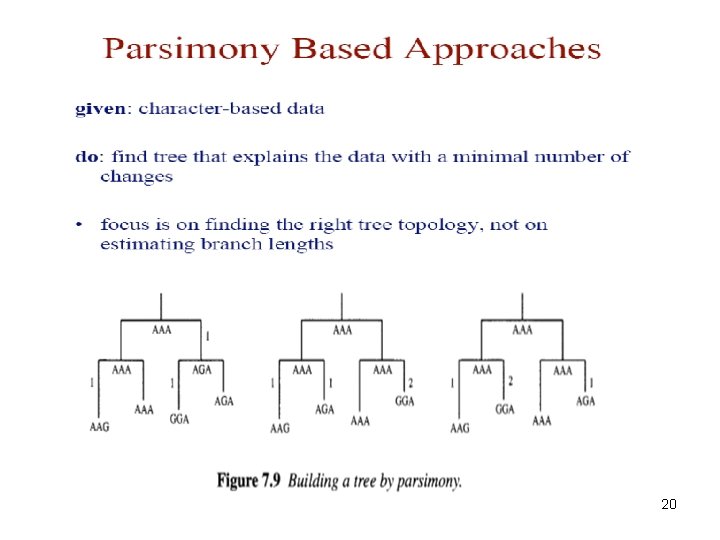
20

21

22

23

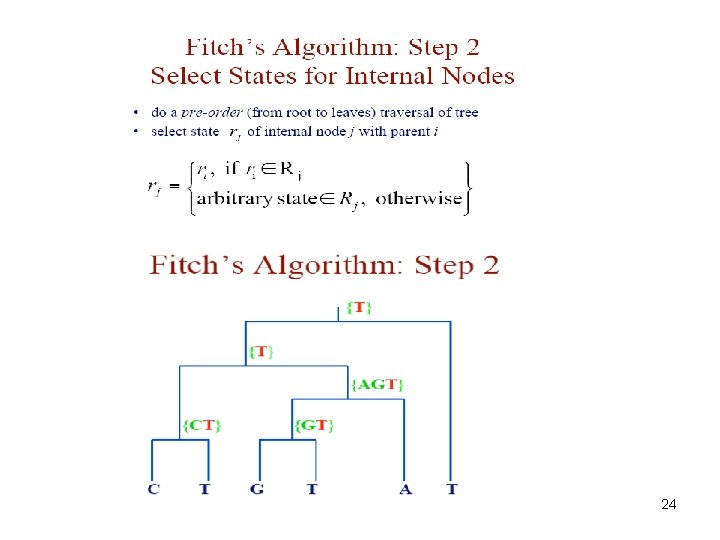
24

25

26

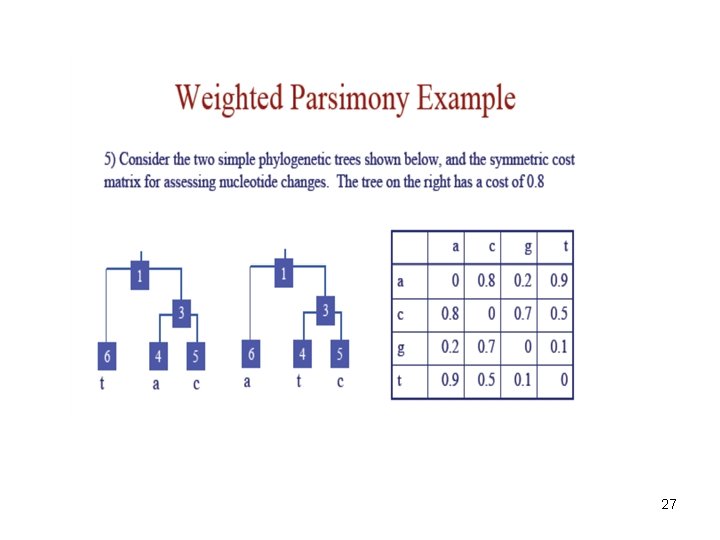
27

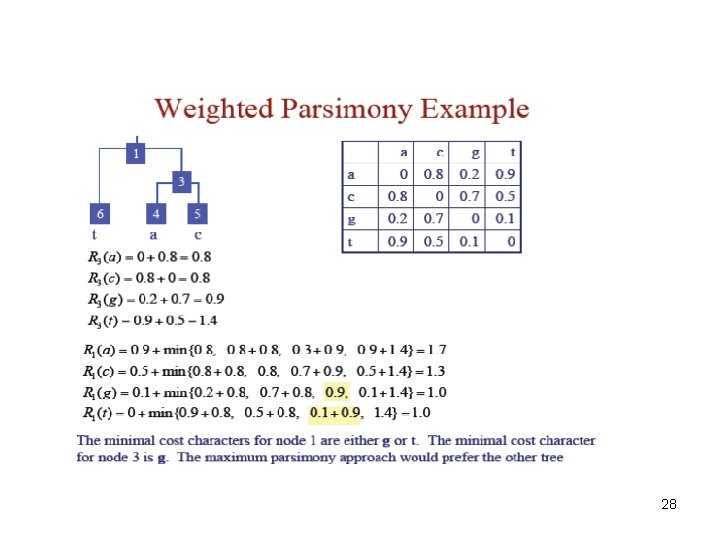
28

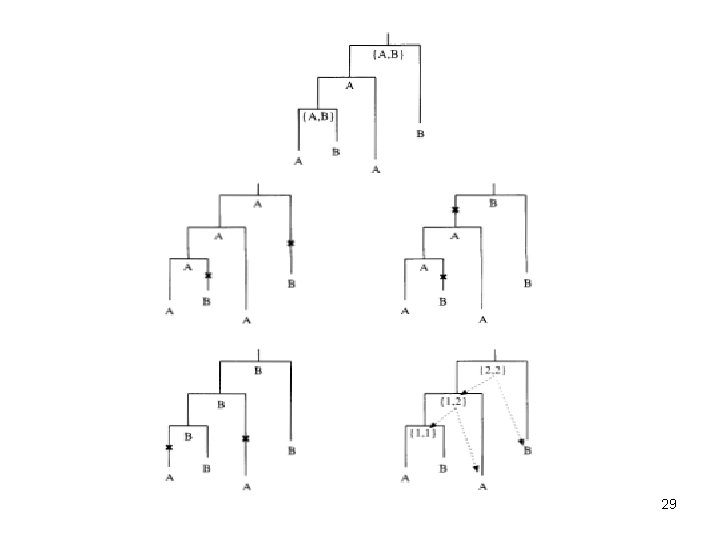
29