Ch 6 Binomial Theory Discrete and Continuous Review

Ch. 6. Binomial Theory

Discrete and Continuous • Review– Are the following discrete or continuous variables? How do you know – Number of credits earned – Heights of students in class – Distance traveled to class tonight – Number of students in class • Preview: Ch. 6 –binomial –discrete • Ch. 7 – normal -- continuous

Recall the 2 coin example from Ch. 4 • Let X= number of heads – New terminology: We call X a “Random Variable” – Note: this variable is discrete • • P(head)= ½ for each coin P(X=0) = 1/4 1 P(X=1)= 2/4 1/2 / P(X=2) = ¼ P(X) X=0 heads X=1 head X=2 heads

Recall 3 coin example • • • Let X= number of heads P(head)= ½ for each coin P(X=0) = 1/8 P(X=1)= 3/8 P(X=2) = 3/8 P(X=3) = 1/8 P(X) 1/2 / P(X) 0 heads 1 head 2 heads 3 heads

Probability Distributions • • Are these probability distributions? Ex 1: P(X=0) =. 25, P(X=1) =. 6, P(X=2) =. 15 Ex 2 : P(X=0) =. 2, P(X=1) =. 5, P(X=2) =. 1 Ex 3: P(X=0) =. 4, P(X=1) = -0. 2, P(X=2) =. 8 Ex 4: P(X=0) =. 2, P(X=1) = 0, P(X=2) =. 8 Ex 5: P(X=0) =. 4, P(X=1) =. 9, P(X=2) = -. 1 Ex 6: P(X=0) =. 2, P(X=1) =. 9, P(X=2) = -. 1

Complement of events • If P(snow today)=. 2, • What is the P(not snow)? • How are these events related? • Another ex: If P(pass)=. 8, P(fail)=?

Binomial Theory

Table 2 in Appendix

3 coin example- binomial theory • • • Let X= number of heads P(head)= ½ for each coin P(X=0) = 3 C 0 * (1/2) 0 (1/2) 3 = 1/8 P(X=1)= 3 C 1 * (1/2) 1 (1/2) 2 = 3/8 P(X=2) = 3 C 2 * (1/2) 2 (1/2) 1 = 3/8 P(X=3) = 3 C 3 * (1/2) 3 (1/2) 0 = 1/8

See p=. 5 column for coin problems See n= 2, 3 for 2, 3 coin problems

Find the probability of observing 3 successes in 5 trials if p = 0. 7. If n=5, P(X=3)= 0. 309

Example: On a 4 question multiple choice test with A, B, C, D, E, p=0. 2, find P(X=3)

Mean and St. Dev. of a Discrete Probability Distribution is the expected value of x = is the standard deviation of x = See book for some general examples. We will just concentrate on a special case: the binomial theory…

Mean and Standard Deviation of a Binomial Distribution

For binomial problems • Mean= • St Dev = • Example: When tossing 6 coins, n = 6, p(head)=. 5, q(tail)=. 5, • Mean = 6(. 5)= 3 heads • St Dev = • = 1. 22

Mean and St Dev Example Calculate the standard deviation of a binomial population with n = 100 and p = 0. 3. a). 21 Answer: C b). 9 c). 4. 5825 d). 4. 41

Birthday problem Let E=probability that at least 2 of us have the same birthday. E-complement= ? ? Recall: P(E)=1 -P(E-complement)

Answer to Bday problem • If n=5, • P(E-complement)= P(365, 5) / 3655=. 973 • So P(E)= 1 -. 973 =. 027 = 2. 7%

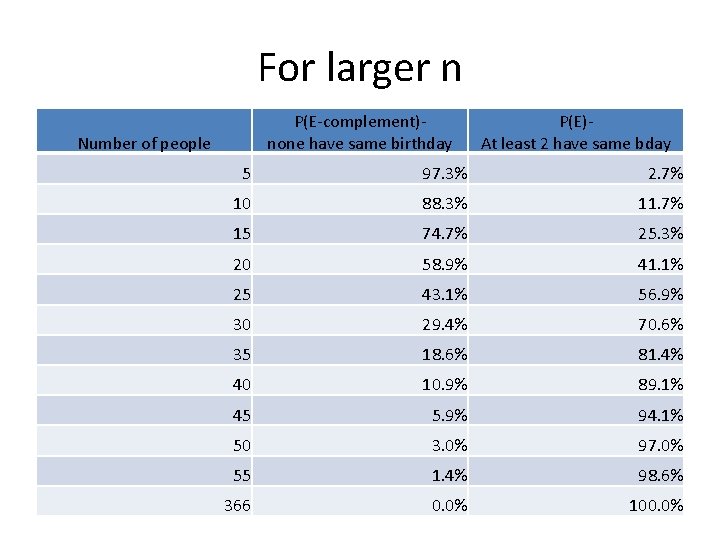
For larger n P(E-complement)none have same birthday Number of people P(E)At least 2 have same bday 5 97. 3% 2. 7% 10 88. 3% 11. 7% 15 74. 7% 25. 3% 20 58. 9% 41. 1% 25 43. 1% 56. 9% 30 29. 4% 70. 6% 35 18. 6% 81. 4% 40 10. 9% 89. 1% 45 5. 9% 94. 1% 50 3. 0% 97. 0% 55 1. 4% 98. 6% 366 0. 0% 100. 0%