Ch 6 2 Similar polygons polygons have same

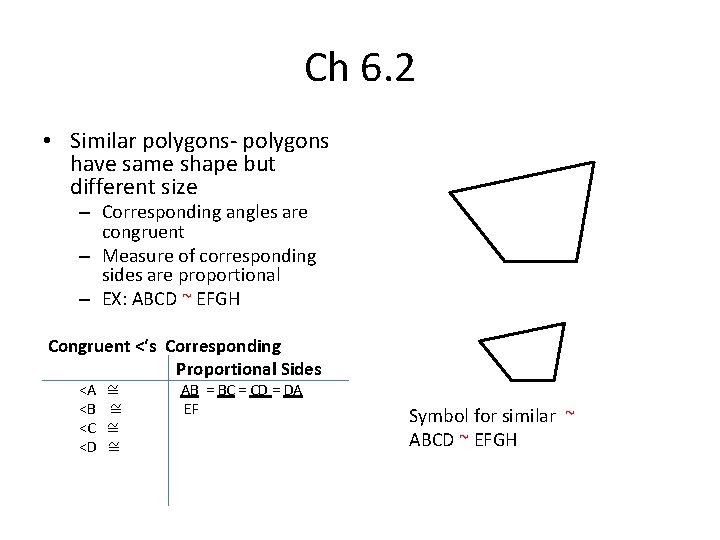
Ch 6. 2 • Similar polygons- polygons have same shape but different size – Corresponding angles are congruent – Measure of corresponding sides are proportional – EX: ABCD ~ EFGH Congruent <‘s Corresponding Proportional Sides <A <B <C <D ≅ ≅ AB = BC = CD = DA EF Symbol for similar ~ ABCD ~ EFGH

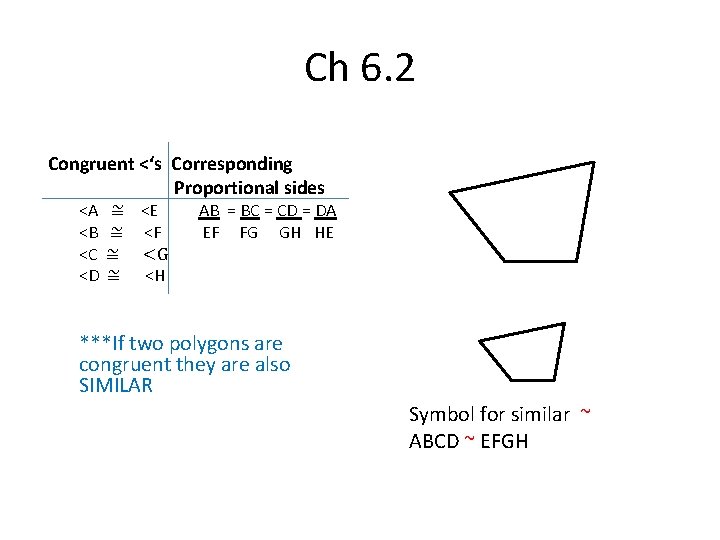
Ch 6. 2 Congruent <‘s Corresponding Proportional sides <A <B <C <D ≅ <E ≅ <F ≅ <G ≅ <H AB = BC = CD = DA EF FG GH HE ***If two polygons are congruent they are also SIMILAR Symbol for similar ~ ABCD ~ EFGH

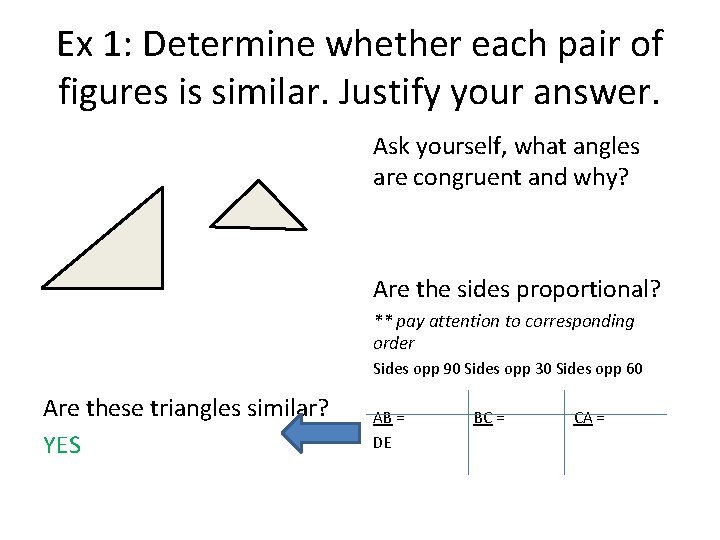
Ex 1: Determine whether each pair of figures is similar. Justify your answer. Ask yourself, what angles are congruent and why? Are the sides proportional? ** pay attention to corresponding order Sides opp 90 Sides opp 30 Sides opp 60 Are these triangles similar? YES AB = DE BC = CA =

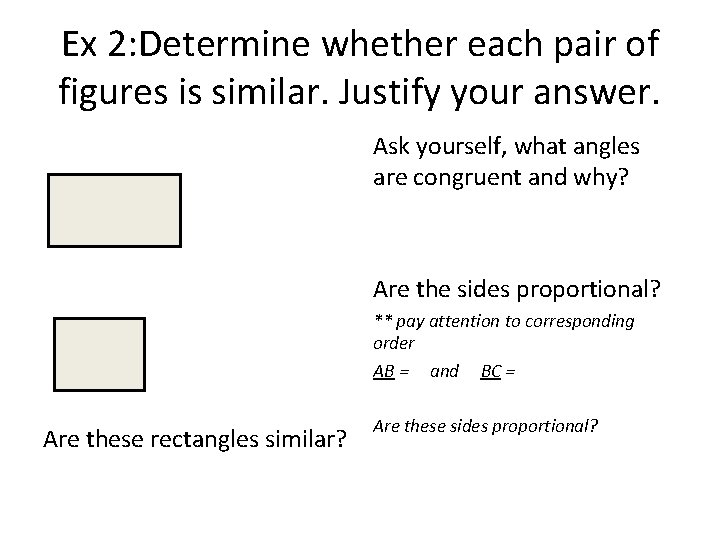
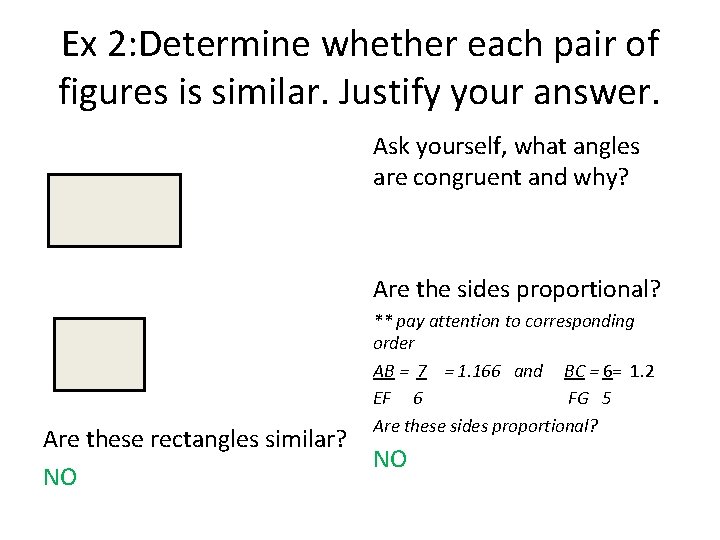
Ex 2: Determine whether each pair of figures is similar. Justify your answer. Ask yourself, what angles are congruent and why? Are the sides proportional? ** pay attention to corresponding order AB = and BC = Are these rectangles similar? Are these sides proportional?

Ex 2: Determine whether each pair of figures is similar. Justify your answer. Ask yourself, what angles are congruent and why? Are the sides proportional? ** pay attention to corresponding order AB = 7 = 1. 166 and BC = 6= 1. 2 EF 6 FG 5 Are these sides proportional? Are these rectangles similar? NO NO

Scale Factor • When you compare the lengths of corresponding sides of similar figures, you usually get a numerical ratio (i. e. FRACTION). • The ratio is called the scale factor of the two figures. • Scale factors are often given for models of real -life objects.

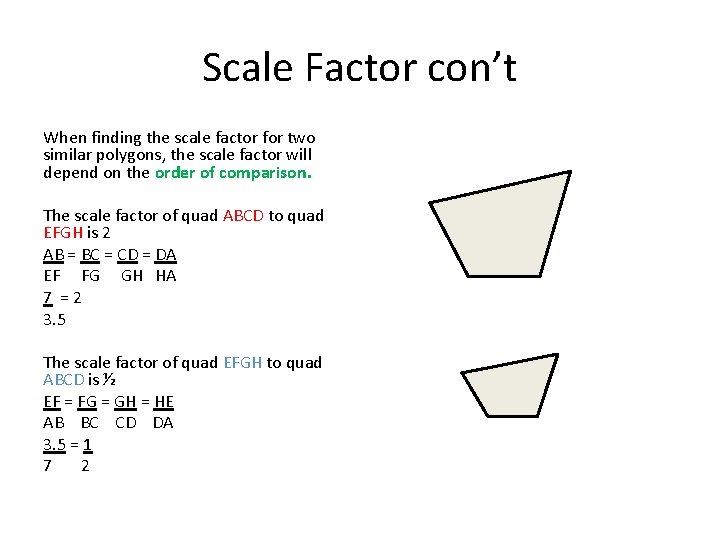
Scale Factor con’t When finding the scale factor for two similar polygons, the scale factor will depend on the order of comparison. The scale factor of quad ABCD to quad EFGH is 2 AB = BC = CD = DA EF FG GH HA 7 =2 3. 5 The scale factor of quad EFGH to quad ABCD is ½ EF = FG = GH = HE AB BC CD DA 3. 5 = 1 7 2

Ex 3: Some special effects in movies are created using miniature models. In a recent movie, a model sports-utility vehicle (SUV) 22 inches long was created to look like a real 14 2/3 foot SUV. What is the scale factor of the model compared to the real SUV? Scale factor = model real • Before finding the scale factor, make sure the measurements use the same unit of measure. Model = ____ Real The ratio comparing the two lengths is ___ or __: __. The scale factor is ___, which means the model is ____ the length of the real SUV.

Ex 3: Some special effects in movies are created using miniature models. In a recent movie, a model sports-utility vehicle (SUV) 22 inches long was created to look like a real 14 2/3 foot SUV. What is the scale factor of the model compared to the real SUV? Scale factor = model real • Before finding the scale factor, make sure the measurements use the same unit of measure. x 12 in = 176 in 1 ft Model = __22 in__ = 1 Real 176 in 8 (14 2/3 ft ) The ratio comparing the two lengths is 1/8 or 1: 8 The scale factor is 1/8 , which means the model is 1/8 the length of the real SUV.

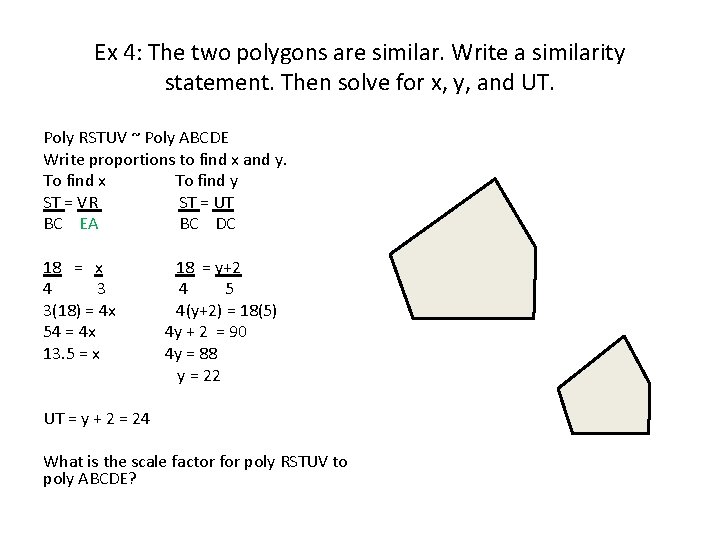
Ex 4: The two polygons are similar. Write a similarity statement. Then solve for x, y, and UT. • Use the congruent angles to write the corresponding vertices in order. Poly ______ ~ Poly ______

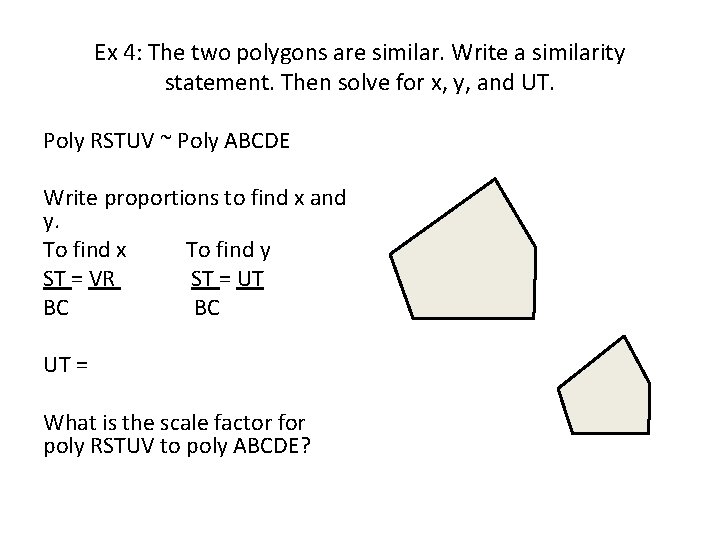
Ex 4: The two polygons are similar. Write a similarity statement. Then solve for x, y, and UT. Poly RSTUV ~ Poly ABCDE Write proportions to find x and y. To find x To find y ST = VR ST = UT BC BC UT = What is the scale factor for poly RSTUV to poly ABCDE?

Ex 4: The two polygons are similar. Write a similarity statement. Then solve for x, y, and UT. Poly RSTUV ~ Poly ABCDE Write proportions to find x and y. To find x To find y ST = VR ST = UT BC EA BC DC 18 = x 4 3 3(18) = 4 x 54 = 4 x 13. 5 = x 18 = y+2 4 5 4(y+2) = 18(5) 4 y + 2 = 90 4 y = 88 y = 22 UT = y + 2 = 24 What is the scale factor for poly RSTUV to poly ABCDE?

EX: 4 What is the scale factor for poly RSTUV to poly ABCDE? • The scale factor is the ratio of the length of any two corresponding sides. ST = 18 = 9 BC 4 2

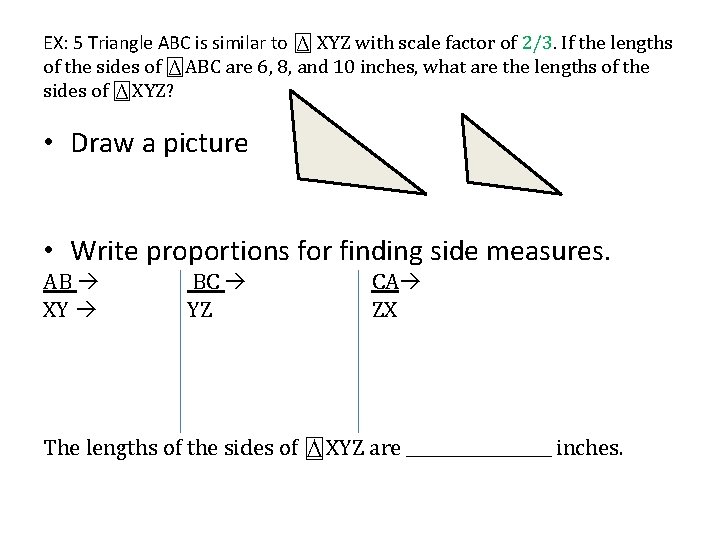
EX: 5 Triangle ABC is similar to ⍍ XYZ with scale factor of 2/3. If the lengths of the sides of ⍍ABC are 6, 8, and 10 inches, what are the lengths of the sides of ⍍XYZ? • Draw a picture • Write proportions for finding side measures. AB XY BC YZ CA ZX The lengths of the sides of ⍍XYZ are _________ inches.

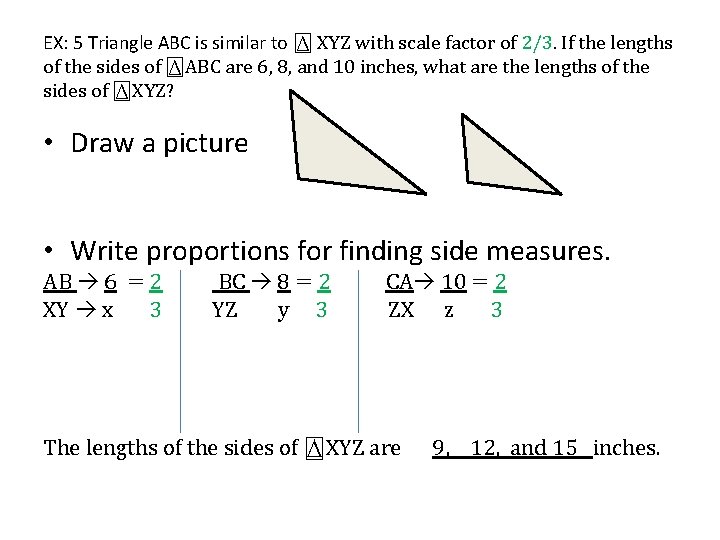
EX: 5 Triangle ABC is similar to ⍍ XYZ with scale factor of 2/3. If the lengths of the sides of ⍍ABC are 6, 8, and 10 inches, what are the lengths of the sides of ⍍XYZ? • Draw a picture • Write proportions for finding side measures. AB 6 = 2 XY x 3 BC 8 = 2 YZ y 3 CA 10 = 2 ZX z 3 The lengths of the sides of ⍍XYZ are 9, 12, and 15 inches.