Ch 5 Population Structure and Changes Population Models

Ch. 5: Population Structure and Changes

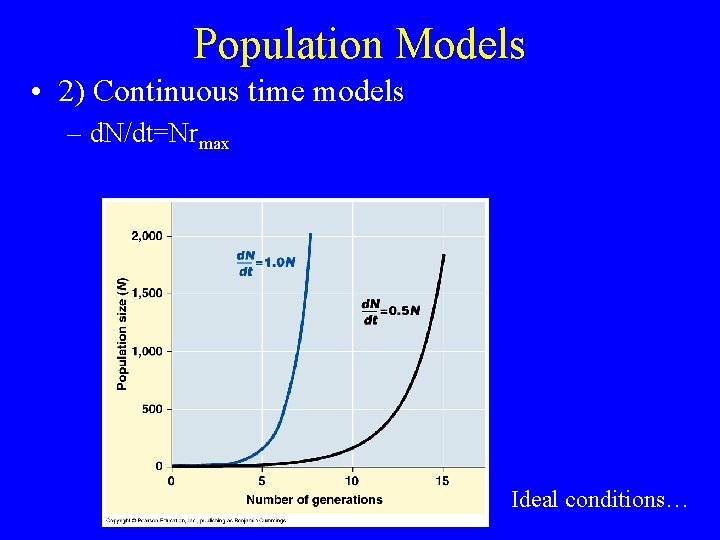
Population Models • 2) Continuous time models – d. N/dt=Nrmax Ideal conditions…

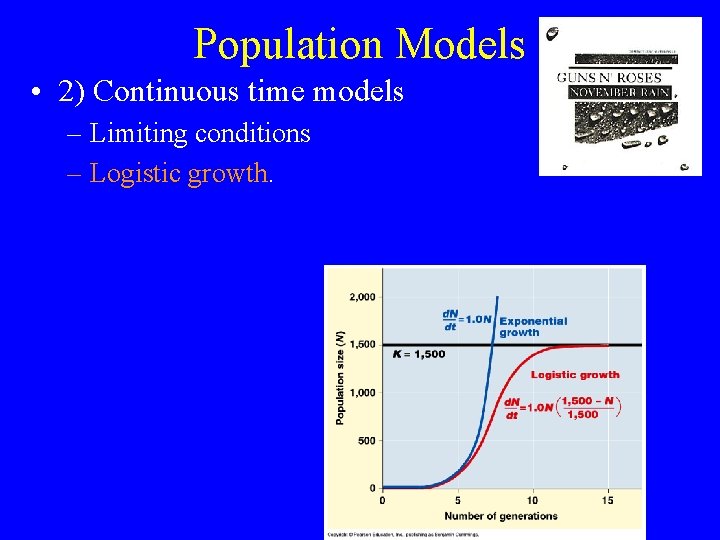
Population Models • 2) Continuous time models – Limiting conditions – Logistic growth.

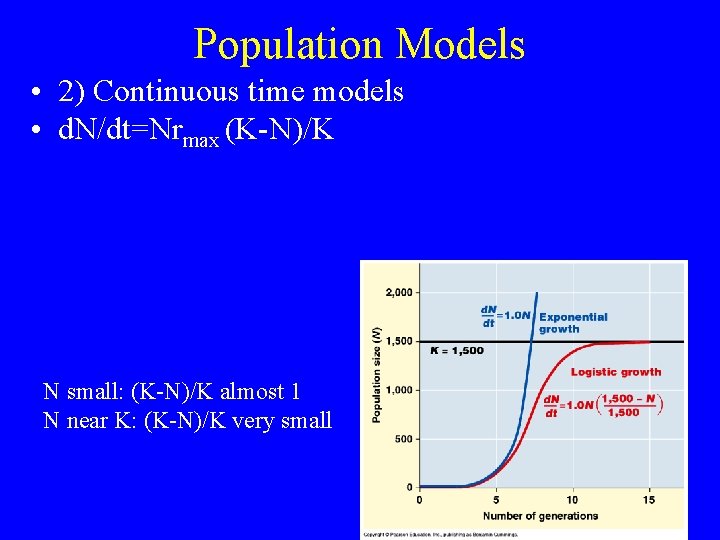
Population Models • 2) Continuous time models • d. N/dt=Nrmax (K-N)/K N small: (K-N)/K almost 1 N near K: (K-N)/K very small

Population Models • • Plant Point 1: K based on density Animals: most individuals have certain size Plants: high modular growth/plasticity Crowding capacity: combine density with biomass per individual.

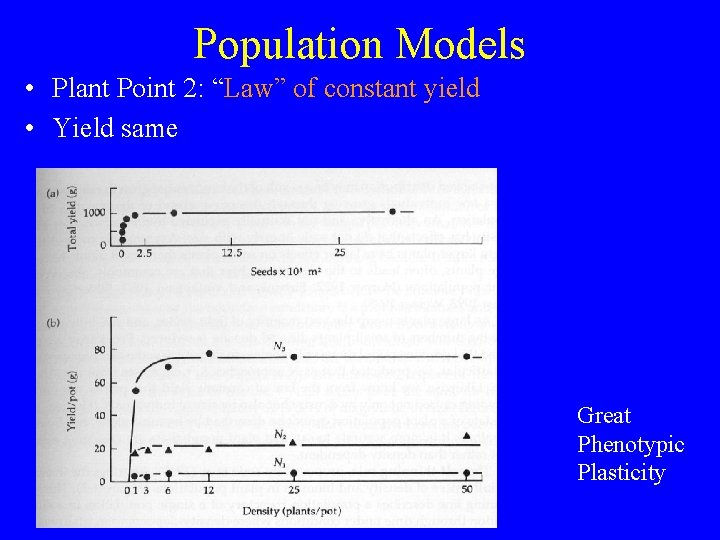
Population Models • Plant Point 2: “Law” of constant yield • Yield same Great Phenotypic Plasticity

Population Models • 3) Discrete-time period models (complex): life tables BIOL 3060 Cemetery lab

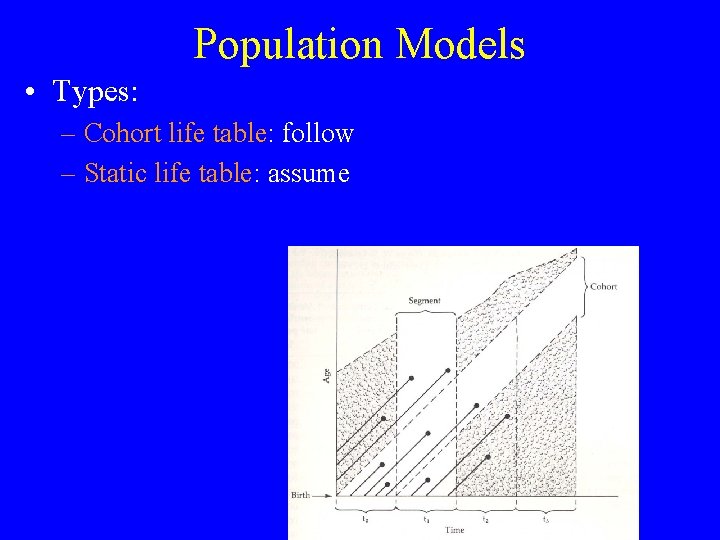
Population Models • Types: – Cohort life table: follow – Static life table: assume

Oldest known tree • Bristlecone Pine (Pinus longaeva). High mtns. How age?

Oldest known tree • Increment borer: extract

Oldest known tree • Oldest was 4, 950 yr (NV mountains)

Oldest known tree • Now oldest (“Methuselah”) 4, 767 yr.

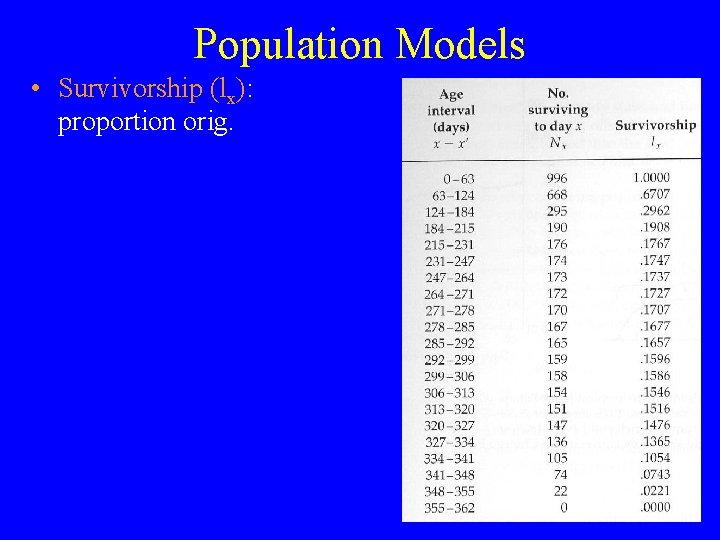
Population Models • Survivorship (lx): proportion orig.

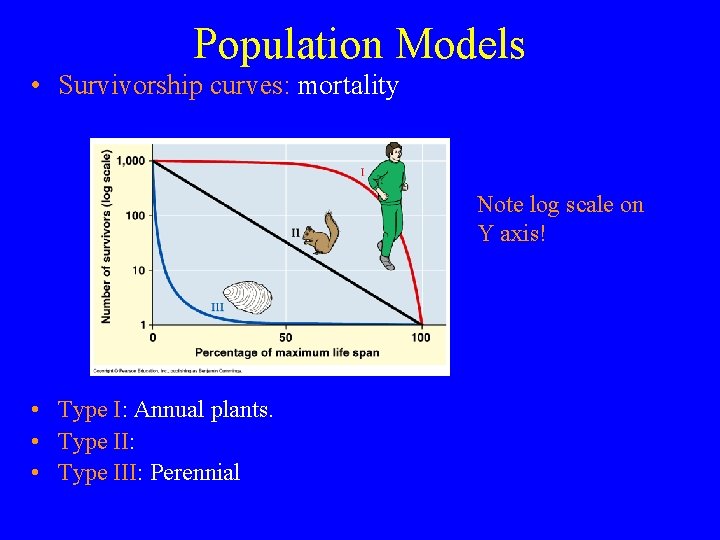
Population Models • Survivorship curves: mortality Note log scale on Y axis! • Type I: Annual plants. • Type II: • Type III: Perennial

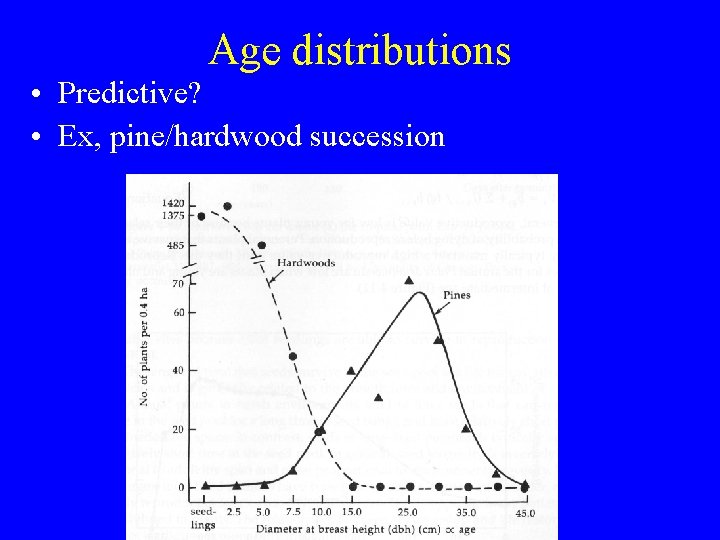
Age distributions • Predictive? • Ex, pine/hardwood succession

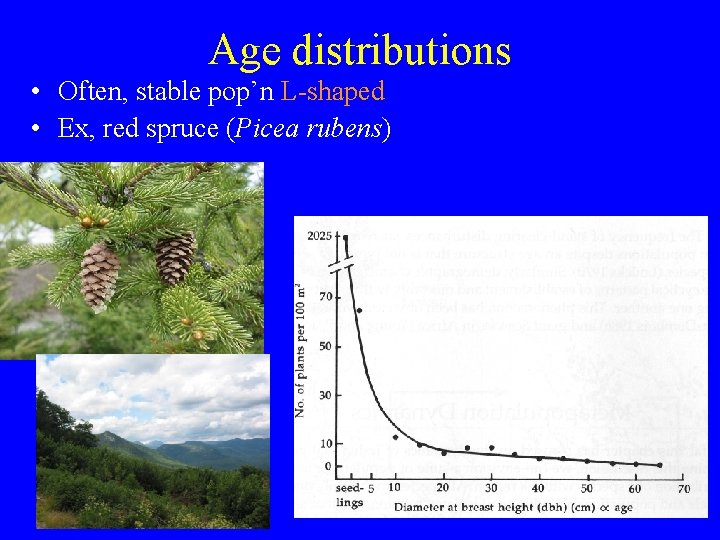
Age distributions • Often, stable pop’n L-shaped • Ex, red spruce (Picea rubens)

Age distributions • Some species: episodic establishment – Sporadic Jack…

Age/stage distributions • Serotinous cones (closed-cone pine) – Seed •

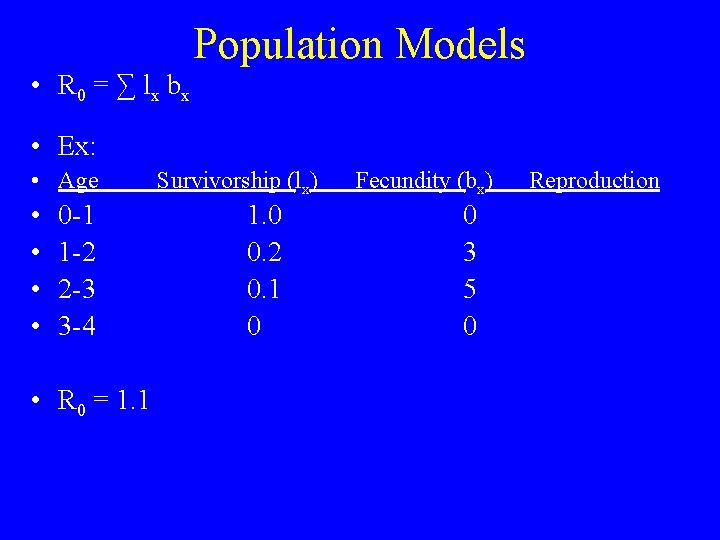
Population Models • 3) Model: life table info + fecundity info • Fecundity: age • Survivorship & fecundity give net reproductive rate (R 0): • R 0 = ∑ lx bx

Population Models • R 0 = ∑ lx bx • Ex: • Age • • 0 -1 1 -2 2 -3 3 -4 • R 0 = 1. 1 Survivorship (lx) 1. 0 0. 2 0. 1 0 Fecundity (bx) 0 3 5 0 Reproduction

Population Models • R 0 >1, • R 0 =1, • R 0 <1,

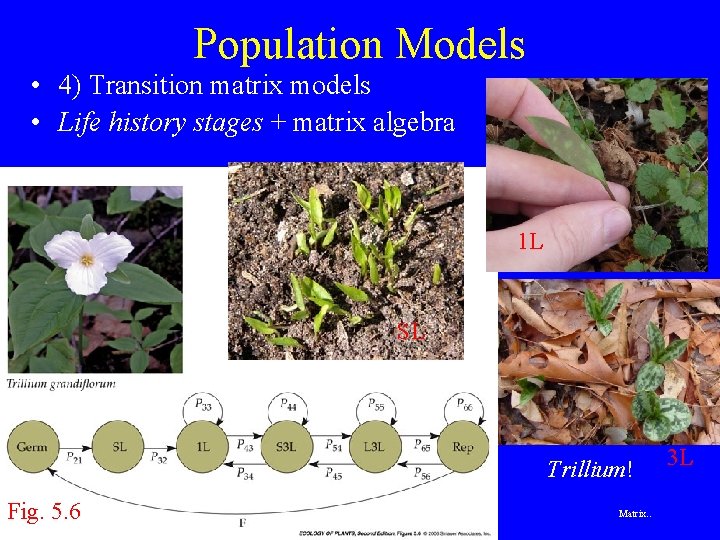
Population Models • 4) Transition matrix models • Life history stages + matrix algebra 1 L SL Trillium! Fig. 5. 6 Matrix. . 3 L

Population Models • Matrix algebra • Matrix: numbers rows/columns

Population Models • Ex: Column matrix (vector) = pop’n status: population vector • Life history stages: s=seeds, r=rosettes, f=flowering 140 # seeds 16 # rosettes 10 # flowering Lab 1: who am I? Rosette forming perennial

Population Models • Transition matrix: probability transition

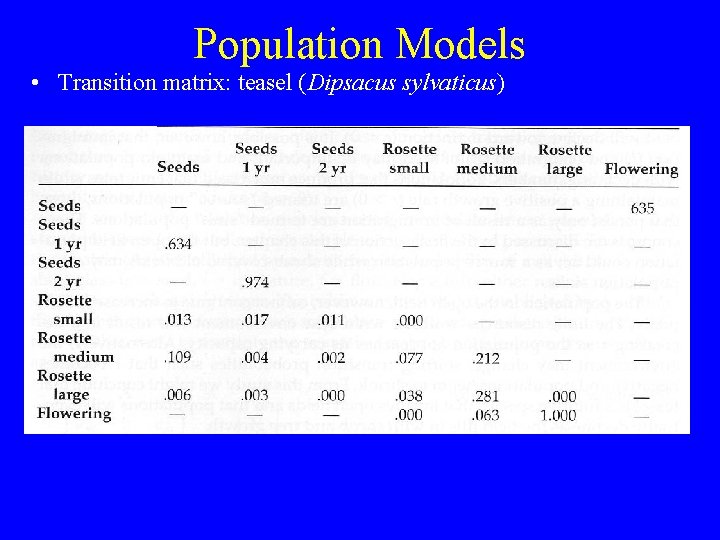
Population Models • Ex: teasel (Dipsacus sylvaticus) • Perennial pasture/roadside weed.

Population Models • Transition matrix: teasel (Dipsacus sylvaticus) Note columns don’t always sum to 1. 0: accounts for mortality

Population Models • Model: pop’n vector X transition matrix • New matrix: pop’n structure next time

Population Models • Ex: 3 stages. Seed, rosette, flowering • Pop’n vector 140 # seeds 20 # rosettes 10 # flowering

Population Models • Ex: 3 stages. Seed, rosette, flowering • Transition matrix year 1 seed year 2 rosette flowering seed 0. 5 0 20 rosette 0. 2 flowering 0 0. 5 0. 1 Note: columns not summing to 1. 0 includes mortality