CH 5 Multivariate Methods 5 1 Multivariate Data





























- Slides: 33

CH. 5: Multivariate Methods 5. 1 Multivariate Data vector: where d-dimensional data attributes/features e. g. , A sample may be represented as a matrix. 1

5. 2 Parameter Estimation Mean vector: Covariance matrix: where variance of covariance of 2

Correlation coefficient: Parameter Estimation Given a sample Sample mean: Sample covariance matrix: Sample correlation matrix: 3

5. 3 Estimation of Missing Values Certain instances have missing attributes. Ignore those instances: not a good idea if the sample is small. Imputation: Fill in the missing value Mean imputation: Substitute the mean of the available data of the missing attribute Imputation by regression: Predict based on other attributes 4

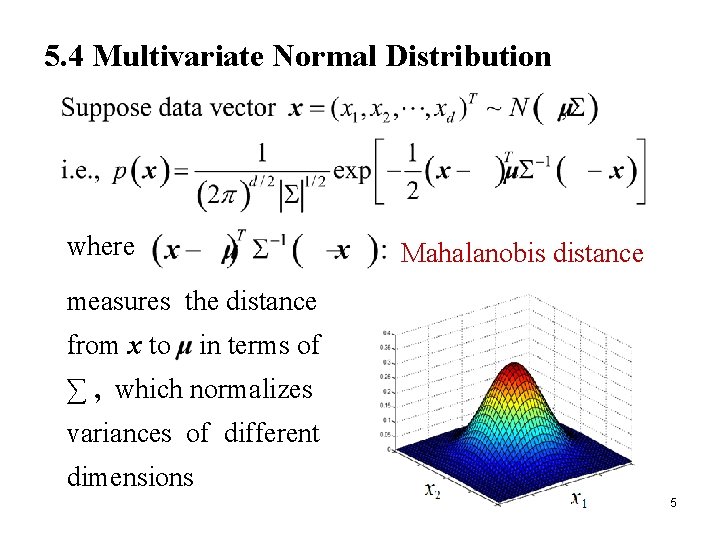
5. 4 Multivariate Normal Distribution where Mahalanobis distance measures the distance from x to in terms of ∑ , which normalizes variances of different dimensions 5

e. g. , d = 1, the square distance from x to in unit. d= 2, 6

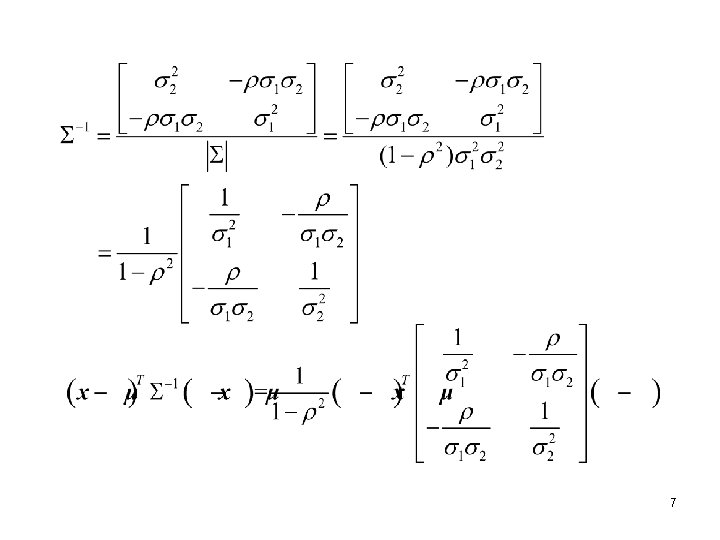
7

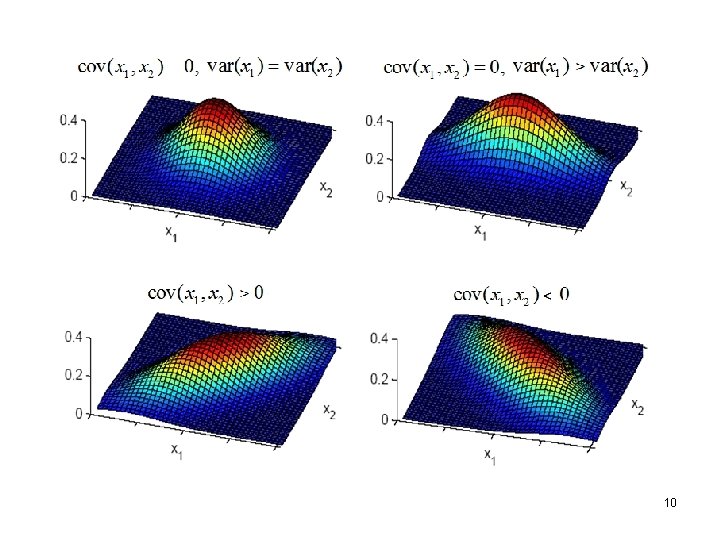
Let (znormalization) Consider 8

the above equation expresses an ellipse. the major axis of the ellipse has a positive (negative) slope. 9

10

: hyperellipsoid centered at Both its shape and orientation are governed by , which normalizes all variables to their unit standard deviations. Let i. e. , The projection of a d-D normal on a vector w is univariate (i. e. , 1 -D) normal. 11

Let W be a matrix. 5. 5 Multivariate Classification From the Bayes’ rule, the posterior probability of Define discriminant function of 12

Given a sample where Estimation of Parameters Substituting into (A) and ignore 13

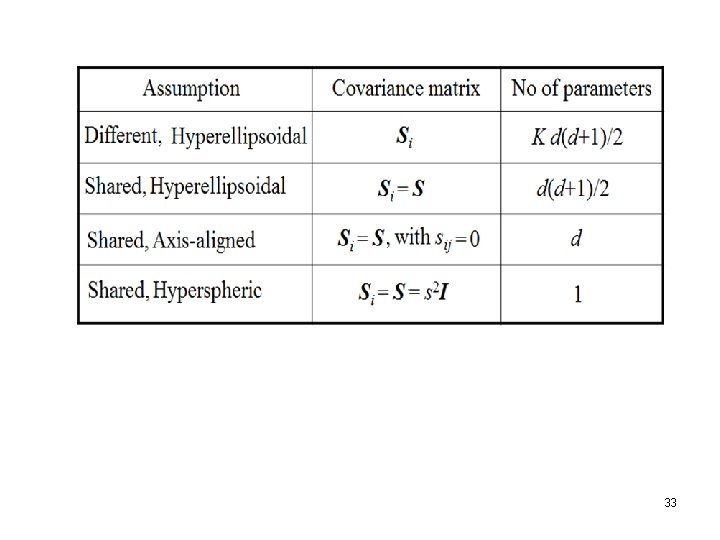
i) Quadratic discriminant: The number of parameters to be estimated is for means and for covariance matrices 14

Share common sample covariance, ignore and . (B) reduces to The numbers of parameters to be estimated: for means and for covariance matrices. Ignoring quadratic term , (C) reduces to 15

ii) Linear discriminant: Assuming off-diagonals of S to be 0, Substitute into 16

Substitute this into (C) 17

iii) Naive Bayes’ classifier: The number of parameters to be estimated is for means and d for covariance matrices. Assuming all variances to be equal, The number of parameters to be estimated is for means and 1 for. 18

Assuming equal priors and ignore s, iv) Nearest mean classifier: Ignore the common term Assuming equal , v) Inner product classifier: 19

5. 6 Tuning Complexity As we increase complexity, bias decreases but variance increases (bias-variance dilemma). 20

5. 7 Discrete Attributes Binary features: where are binary. If xj ’s are independent, The discriminant function: 21

Multinomial features: Define Let : the probability that takes value , i. e. , If xj ’s are independent, The discriminant function: 22

5. 8 Multivariate Regression Linear multivariate model Assume Then, maximizing the likelihood minimizing the sum of squared error Taking derivatives wrt , respectively, 23

In vector-matrix form: Solution: , where 24

Generalizing the linear i) model: A polynomial model can lead to a linear multivariate model by letting Example: Find a quadratic model of two variables to fit a sample i. e. , determine Answer: Write the fit as 25

where Use linear regression to learn A nonlinear model can lead to a linear multivariate model. 26

Summary Multivariate methods -- deal with multivariate data. Multivariate data: where attributes/features Multivariate parameters of interest: Mean vector: 27

Covariance matrix: where Correlation matrix: 28

Imputation: estimating missing values Mean imputation: Substitute the mean of the available data of the missing attribute Imputation by regression: Predict based on other attributes Multivariate Normal Distribution 29

Mahalanobis distance measures the distance from x to in terms of ∑, which normalizes variances of different dimensions. : hyperellipsoid centered at Both its shape and orientation are governed by , which normalizes all variables to their unit standard deviations. Let i. e. , The projection of a d-D normal on a vector w is univariate (i. e. , 1 -D) normal. 30

Let W be a matrix. Multivariate Classification i) Quadratic discriminant: ii) Linear discriminant: 31

iii) Naive Bayes’ classifier: iv) Nearest mean classifier: v) Inner product classifier: 32

33