Ch 5 Laplace Transform Company LOGO 1 Company

























































- Slides: 67

Ch # 5 Laplace Transform Company LOGO 1

Company LOGO Topics 1. Get to know: Laplace Transform 2. Laplace Theory and Properties 3. Applications 2

Company LOGO Get to know: Laplace Transform § Widely used to solve Linear Ordinary Differential Equation )สมการอนพนธสามญเชงเสน ( § With known initial value problems § Laplace Transform: 3 Fundamental steps Step #1: The given ODE is transformed into an algebraic equation called “subsidiary equation” Step #2: The “subsidiary equation” is solved by purely algebraic operations Step #3: The solution in Step 2 is transformed back, resulting in the solution of the given problem 3

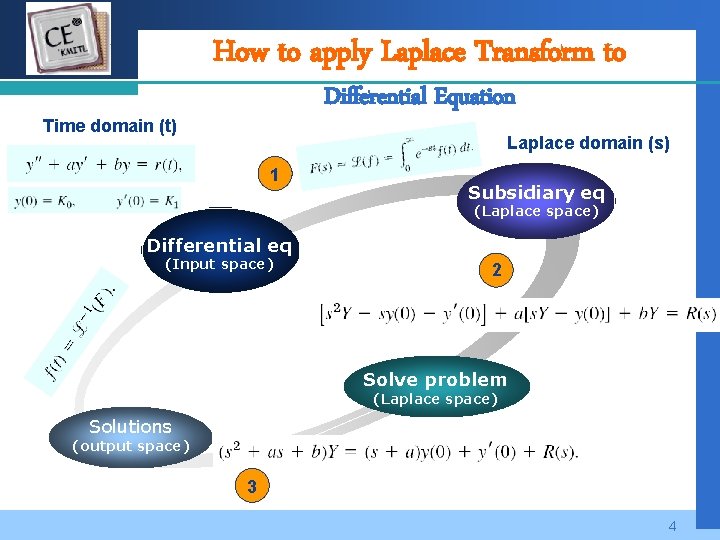
Company How to apply Laplace Transform to LOGO Differential Equation Time domain (t) Laplace domain (s) 1 Subsidiary eq (Laplace space) Differential eq (Input space) 2 Solve problem (Laplace space) Solutions (output space) 3 4

Company LOGO Step #1: Forward Laplace Transform �������� integrate ���� 5

Company LOGO Inverse Laplace Transform 6

Company LOGO Laplace Transform (Example#1) The interval of integration in (1) is infinite, such an integral is called improper integral § Laplace transform of a unit function is 1/s L(1) = 1/s 7

Company LOGO Laplace Transform (Example#2) Integration by part 8

Company LOGO 9

Company LOGO Laplace Transform Properties § Linearity คณสมบตเชงเสนของการแปลงลาปลาซ § First Shifting Theorem คณสมบตการเลอนใน S space (laplace space( § Laplace of Differential Equation § Laplace of Integral Equation § Second Shifting Theorem คณสมบตการเลอนใน t space (time space( § Differentiation of Laplace Transform § Integration of Laplace Transform 10

Company LOGO Proof: 11

Company LOGO Proof: 12

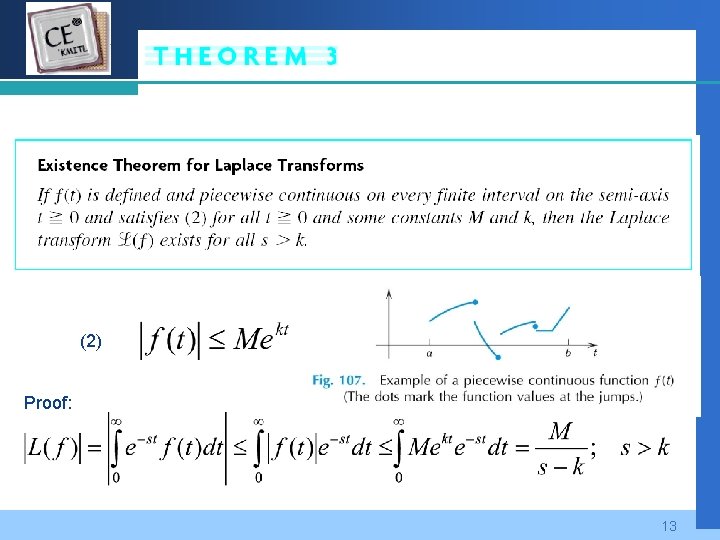
Company LOGO (2) Proof: 13

Company LOGO Non-existence of Laplace Transform Existence of Laplace Transform Non-existence of Laplace Transform 14

Company LOGO Integration by part 15

Company LOGO Helpful of Laplace Transform of Derivative 1. Solving Laplace Transform of complicated f(t) using Laplace Derivative of f(t) no actual integration of Laplace Transform 2. Solving Linear ODE System 16

Company LOGO Solve Laplace Transform of complicated f(t) What is Direct Method Indirect Method using Relation to Laplace of Derivative initial condition Derivative of f(t) Relation to Laplace of Derivative no actual integration of Laplace Transform

Company LOGO Solving Linear ODE System using Laplace Differential Equations: Initial Value Problems Continued

Company LOGO Continued

Company LOGO

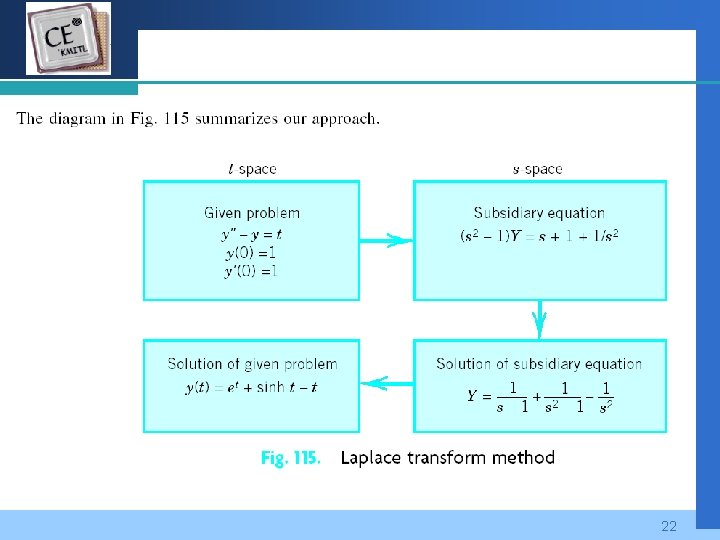
Company LOGO Slide 9 Continued 21

Company LOGO 22

Company LOGO 23


Company LOGO 25

Company LOGO Second Shifting Theorem: time shifting (t-shifting) (2) 26

Company LOGO Second Shifting Theorem: time shifting (t-shifting) 27

Company LOGO 28

Company LOGO Continued 29

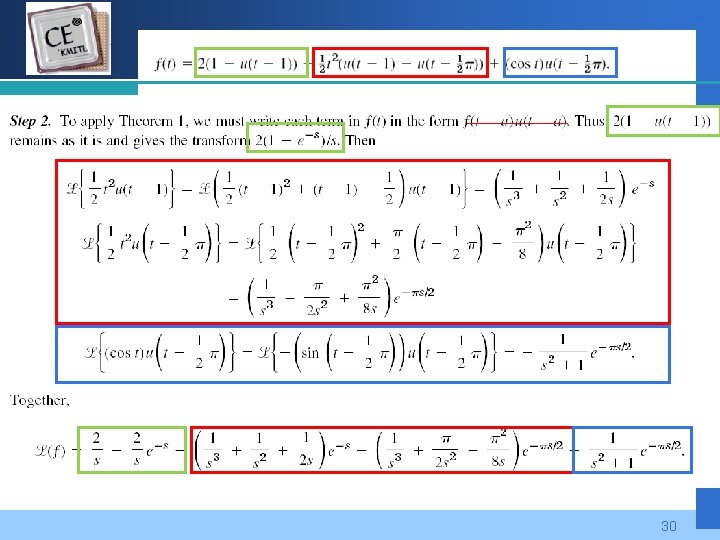
Company LOGO 30

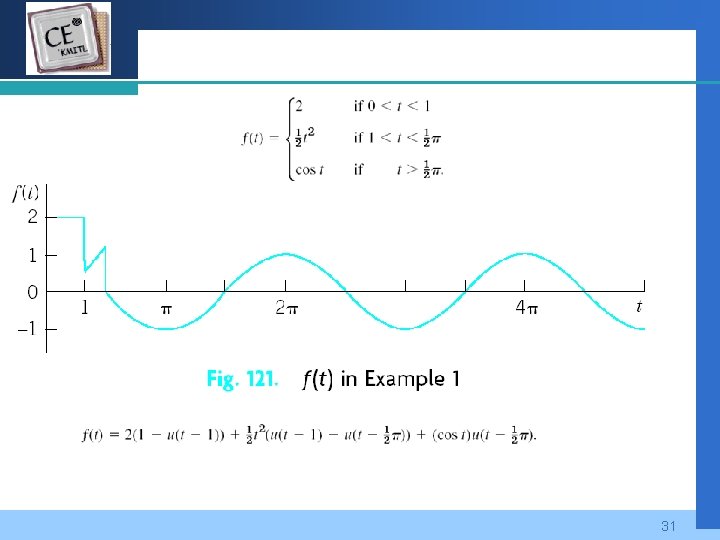
Company LOGO 31

Company LOGO If the conversion of f(t) to f(t-a) is inconvenient, replace it by (4**) ใชสตร 1, 2, 3 จากตาราง 6. 9 32

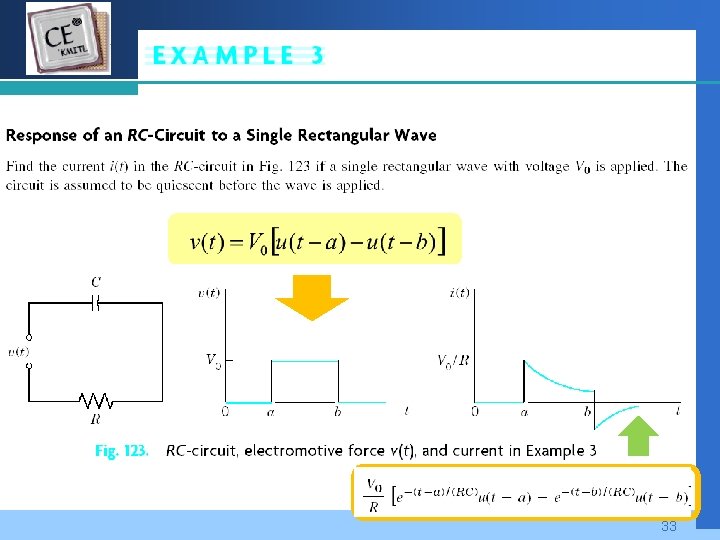
Company LOGO 33

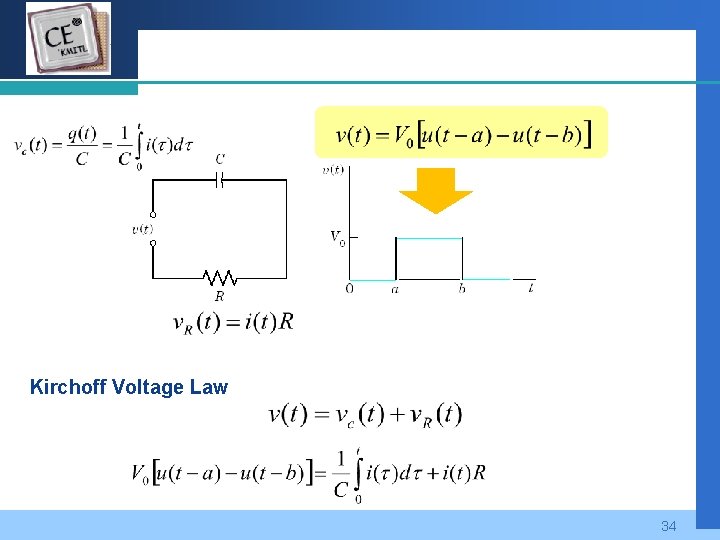
Company LOGO Kirchoff Voltage Law 34

Company LOGO Take Laplace Transform of Both sides 35

Company LOGO Slide 22 Laplace transform of integral Formula (2), slide 25 Formula (7), table 6. 9 (4*), slide 27 36

Company LOGO Short Impulses : Dirac’s Delta function Continued 37

Company LOGO Continued 38

Company LOGO Pages 241 -243 c Continued 39

Company LOGO 40

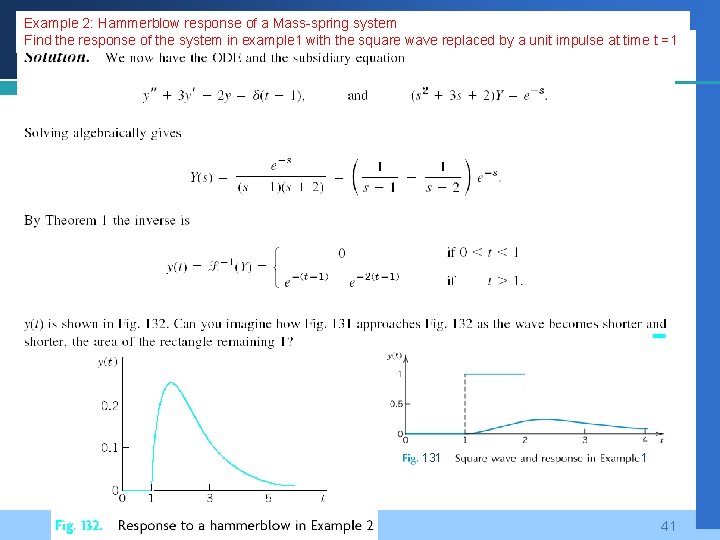
Example 2: Hammerblow response of a Mass-spring system Company Find the response of the system in example 1 with the square wave replaced by a unit impulse at time t =1 LOGO Page 244 131 1 41

Company LOGO 42

Company LOGO L{h(t)} 43

Company LOGO Pages 251 -252 44

Company LOGO 45

Company LOGO Differentiation of Laplace Transform 46

Company LOGO Differentiation of transforms. Formula 21 -23 in Table 6. 9 47

Company LOGO Differentiation of Laplace Transform 48

Company LOGO Differentiation of Laplace Transform 49

Company LOGO Integration of Laplace Transform 50

Company LOGO Systems of ODEs Continued 51

Company LOGO 52

Company LOGO Continued 53

Company LOGO Continued 54

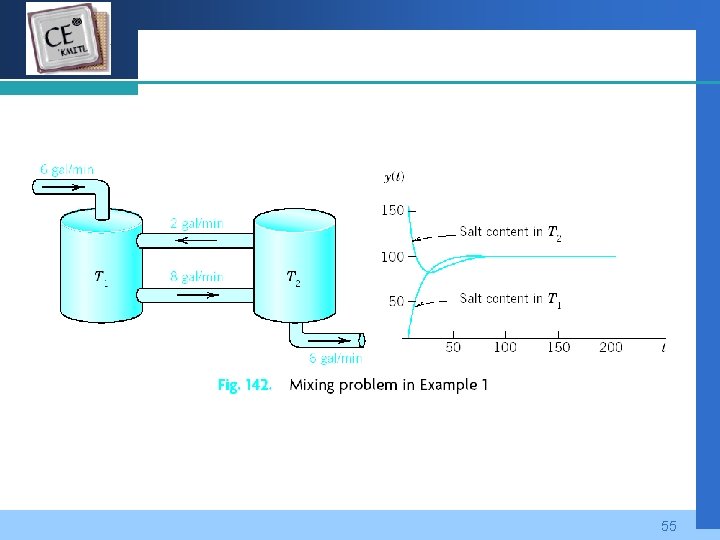
Company LOGO 55

Company LOGO Page 264 a Continued 56

Company LOGO Page 264 b Continued 57

Company LOGO 58

Company LOGO Pages 265 -267 a Continued 59

Company LOGO Pages 265 -267 b Continued 60

Company LOGO Continued 61

Company LOGO Pages 265 -267 d Continued 62

Company LOGO Continued 63

Company LOGO 64

Page 269 a Continued

Page 269 b Continued

Page 269 c