Ch 5 Forces and Newtons Laws Defining Force

Ch. 5 Forces and Newton’s Laws

Defining Force Questions: l What is a force? l What is the connection between force and motion? Definitions: l A force is a push or pull on an object. l A force is a vector. It has both magnitude and direction. l A force requires an agent. Something must do the pushing and pulling. l A force is either a contact force or a long-range force. Gravity is the only long-range force we will consider until Physics 222

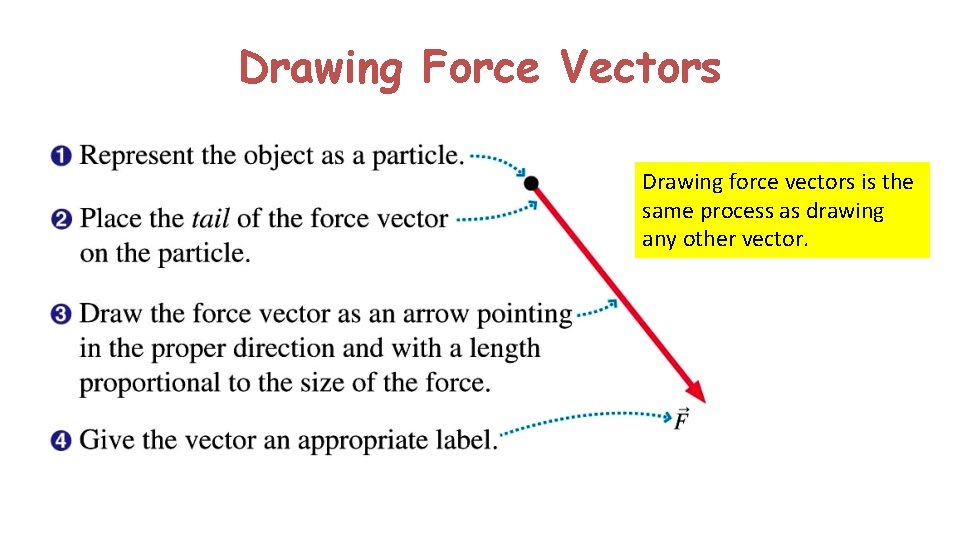
Drawing Force Vectors Drawing force vectors is the same process as drawing any other vector.

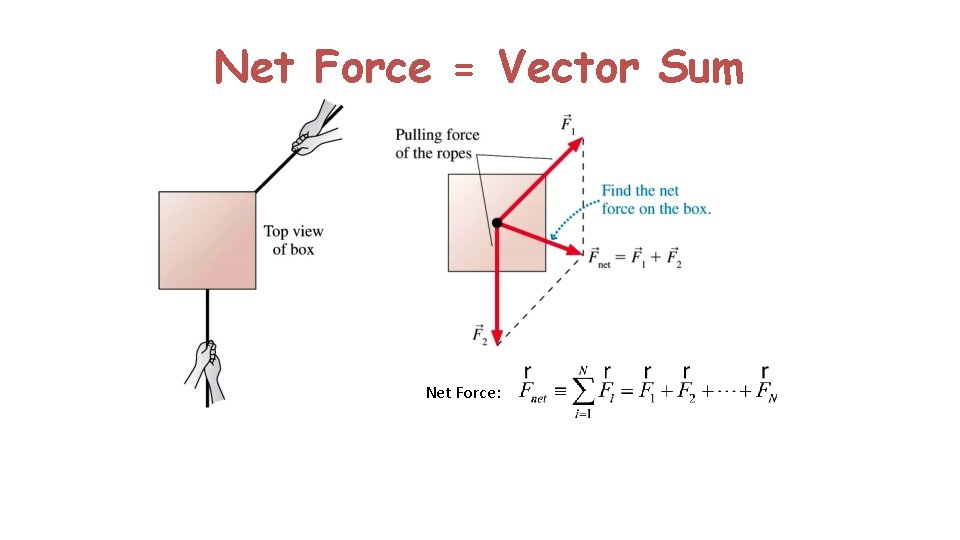
Net Force = Vector Sum Net Force:

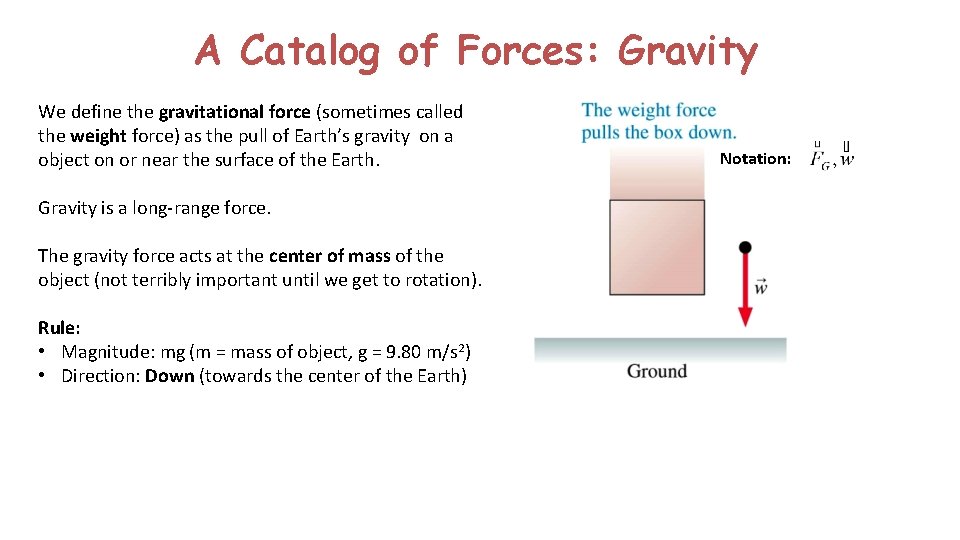
A Catalog of Forces: Gravity We define the gravitational force (sometimes called the weight force) as the pull of Earth’s gravity on a object on or near the surface of the Earth. Gravity is a long-range force. The gravity force acts at the center of mass of the object (not terribly important until we get to rotation). Rule: • Magnitude: mg (m = mass of object, g = 9. 80 m/s 2) • Direction: Down (towards the center of the Earth) Notation:

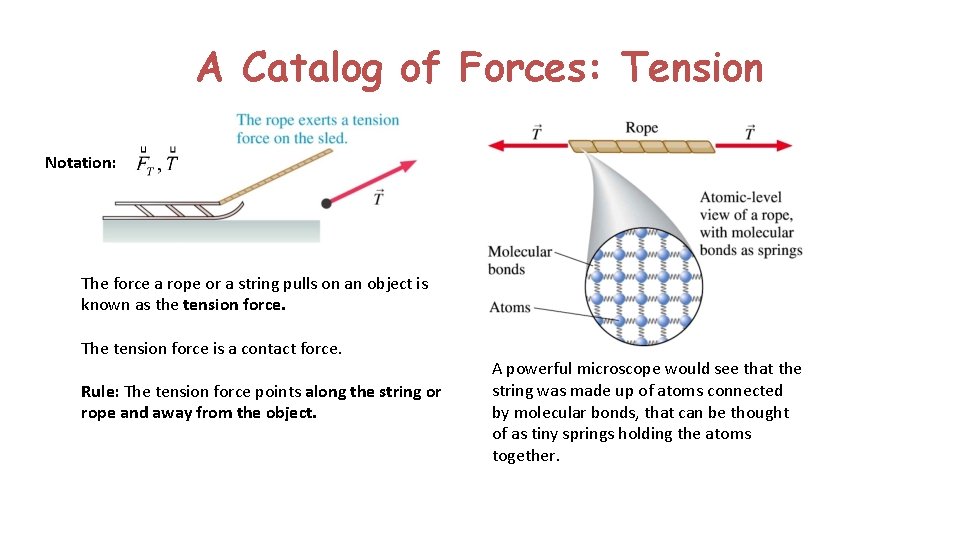
A Catalog of Forces: Tension Notation: The force a rope or a string pulls on an object is known as the tension force. The tension force is a contact force. Rule: The tension force points along the string or rope and away from the object. A powerful microscope would see that the string was made up of atoms connected by molecular bonds, that can be thought of as tiny springs holding the atoms together.

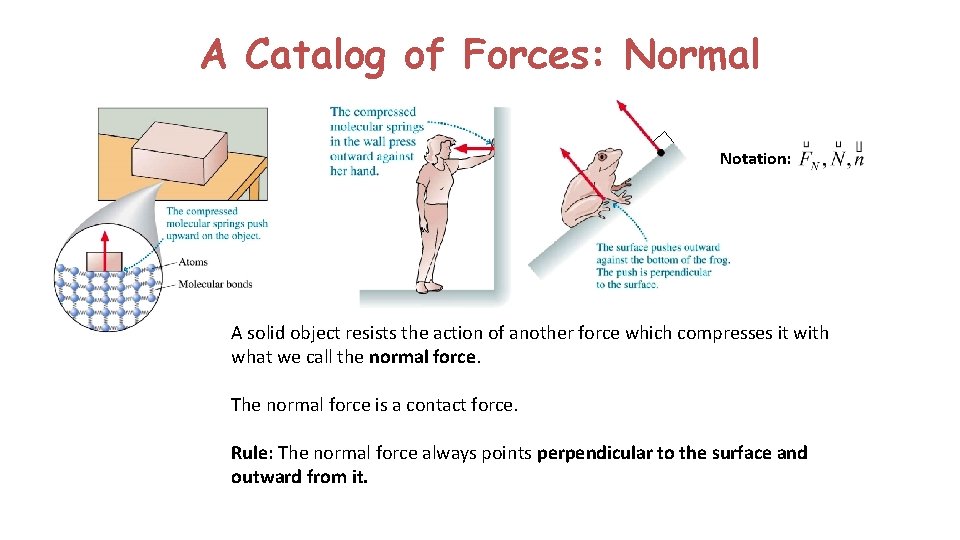
A Catalog of Forces: Normal Notation: A solid object resists the action of another force which compresses it with what we call the normal force. The normal force is a contact force. Rule: The normal force always points perpendicular to the surface and outward from it.

Symbols for Forces The notations here are used in your textbook; other notations are used. Be sure to label your forces appropriately! We seek to build a visual diagram labeling all the individual forces exerted on an object – we call this the free-body diagram (FBD).

Free-Body Diagram (FBD) Rules l Identify “the system” and “the environment. ” The system is the object whose motion you wish to study; the environment is everything else. l Draw a picture of the situation. Show the object—the system—and everything in the environment that touches the system. Ropes, springs, and surfaces are all parts of the environment. (Optional: Represent the object as a point particle) l (Optional) Draw a closed curve around the system. Only the object is inside the curve; everything else is outside. l Name and label each contact force acting on the object. There is at least one force at each point of contact; there may be more than one. When necessary, use subscripts to distinguish forces of the same type. l Name and label each long-range force acting on the object. For now, the only long-range force is gravity.

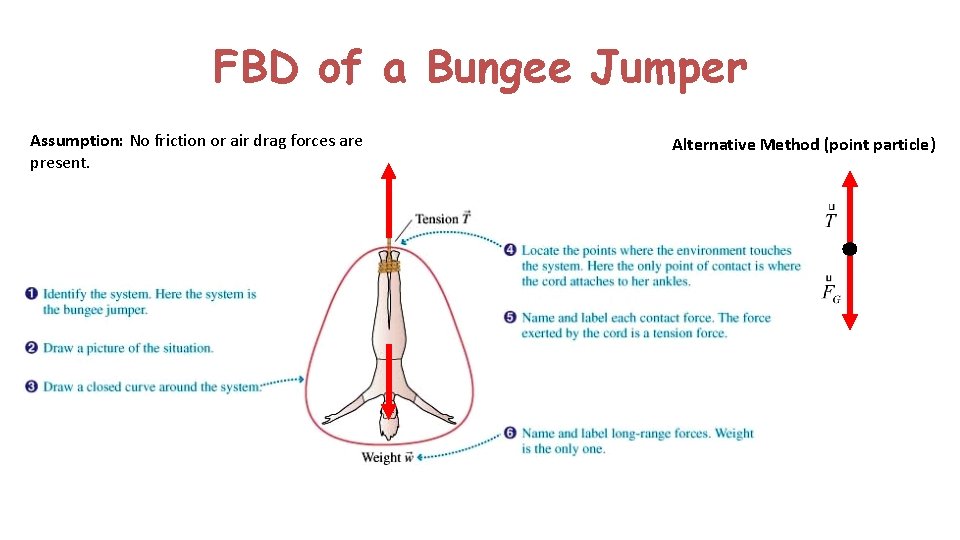
FBD of a Bungee Jumper Assumption: No friction or air drag forces are present. Alternative Method (point particle)

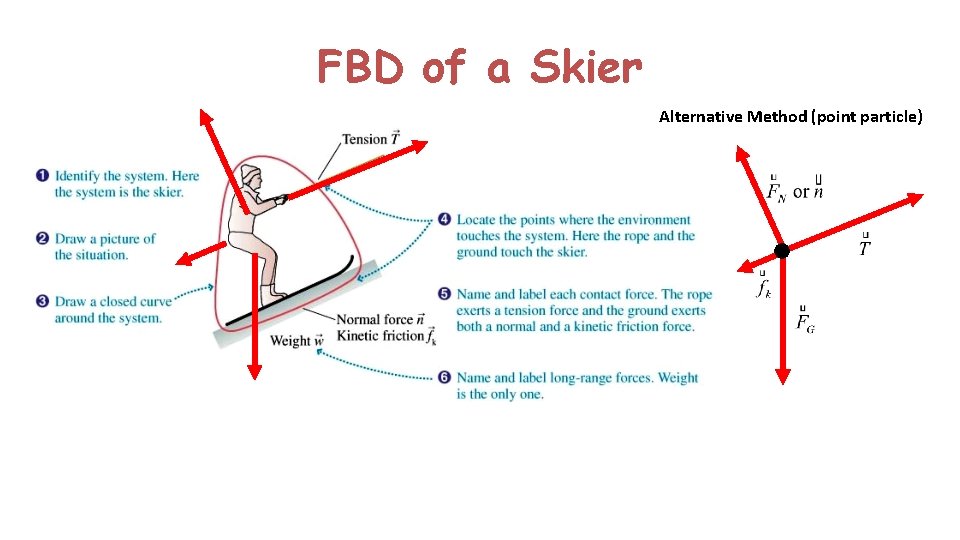
FBD of a Skier Alternative Method (point particle)

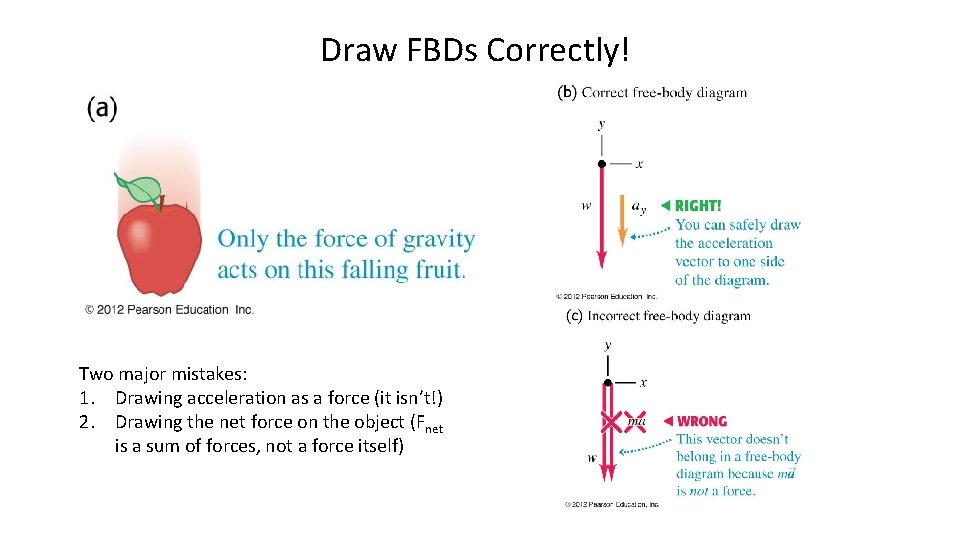
Draw FBDs Correctly! Two major mistakes: 1. Drawing acceleration as a force (it isn’t!) 2. Drawing the net force on the object (Fnet is a sum of forces, not a force itself)

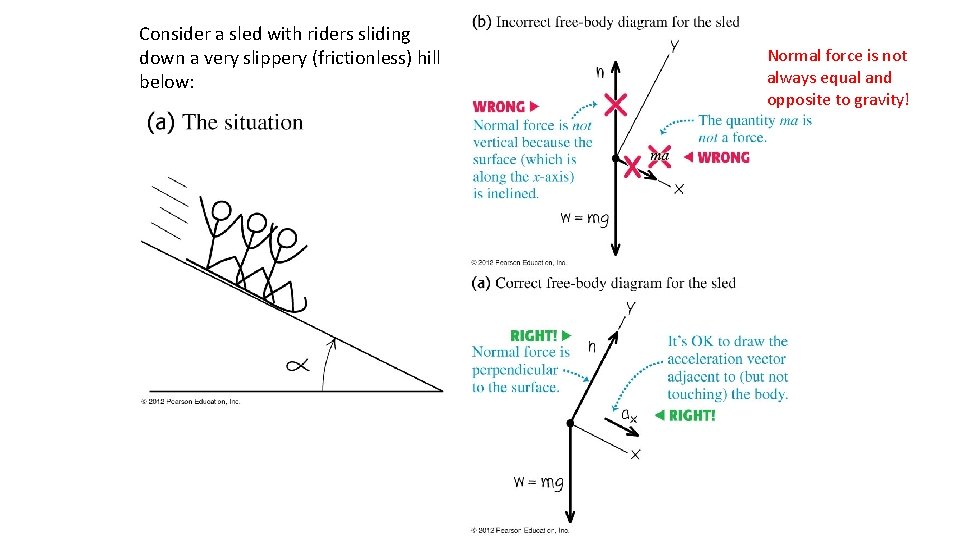
Consider a sled with riders sliding down a very slippery (frictionless) hill below: Normal force is not always equal and opposite to gravity!

Summary • • • Forces are vectors. They have a magnitude and direction and add like vectors. Forces are either contact or long-range. Each force has certain rules that describe their interaction. Know them! FBDs are catalogues of the individual forces exerted on an object. Acceleration and net force are not “pushes” or “pulls” and therefore do not belong on FBDs!

Isaac Newton (1642 -1727) was the first to realize how to use forces, which are pushes or pulls, to understand motion.

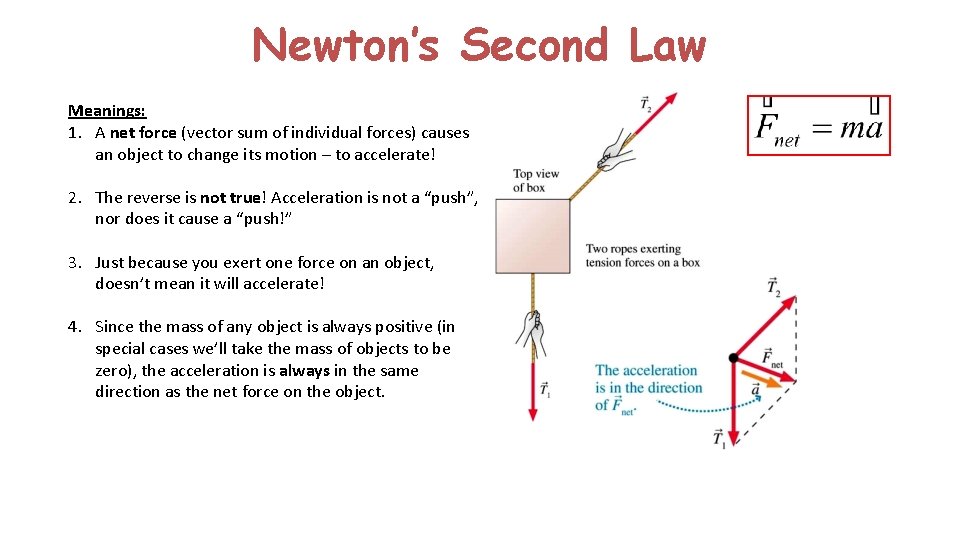
Newton’s Second Law Newton’s 2 nd Law: An object of a given mass m subjected to forces will undergo an acceleration a given by: or where (net force is the vector sum of the individual forces) Units: Newton (N) 1 N = 1 kg∙m/s 2

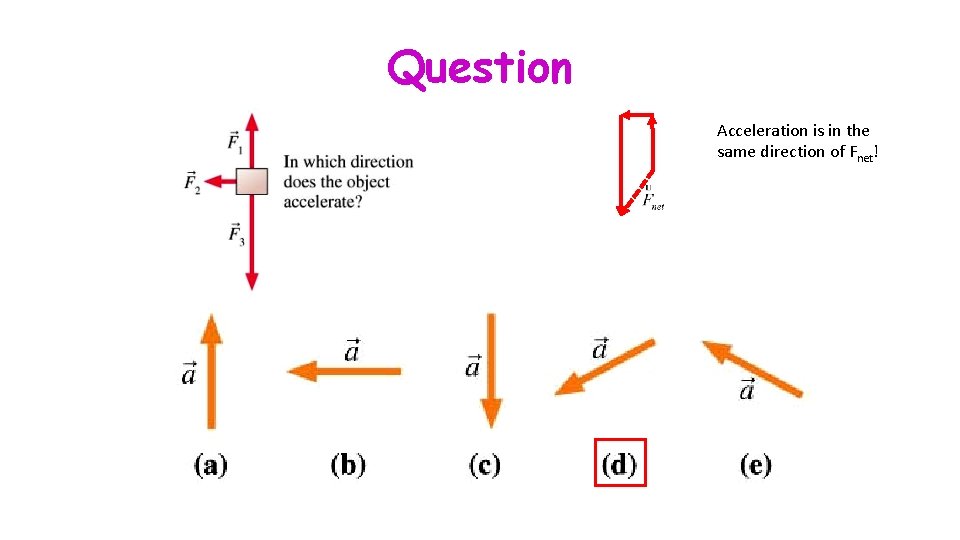
Newton’s Second Law Meanings: 1. A net force (vector sum of individual forces) causes an object to change its motion – to accelerate! 2. The reverse is not true! Acceleration is not a “push”, nor does it cause a “push!” 3. Just because you exert one force on an object, doesn’t mean it will accelerate! 4. Since the mass of any object is always positive (in special cases we’ll take the mass of objects to be zero), the acceleration is always in the same direction as the net force on the object.

Question Acceleration is in the same direction of Fnet!

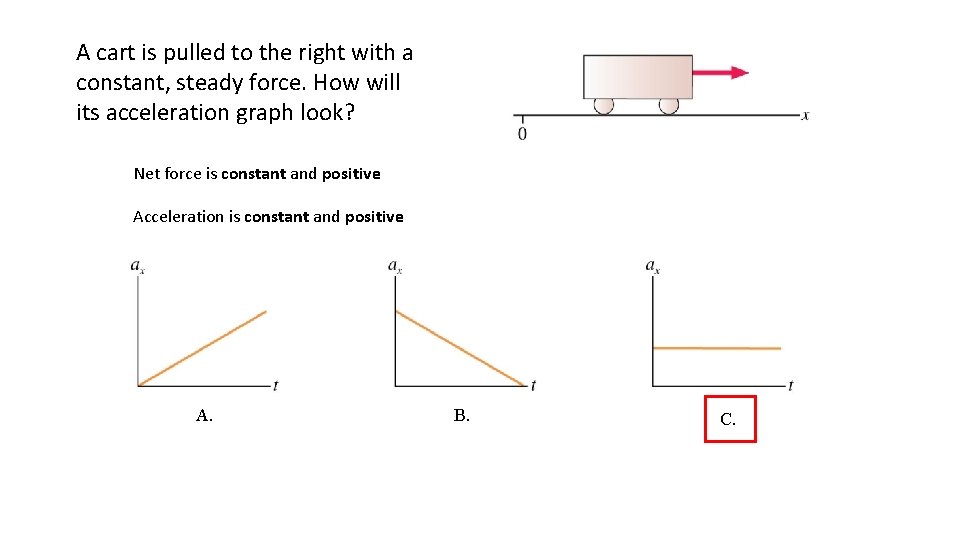
Quick. Check 5. 6 A cart is pulled to the right with a constant, steady force. How will its acceleration graph look? Net force is constant and positive Acceleration is constant and positive A. B. C.

A ball that rolls down a smooth inclined track will climb back on a track that is tilted upward to nearly the same height it had before it was released. Galileo wrote that if the ball went onto a frictionless level track it would roll on indefinitely.

Isaac Newton later put this idea down precisely in his “first law. ” A body at rest will remain at rest, and a body in motion will continue to move in a straight line with constant speed --- unless an unbalanced, or net, force acts on it.

Newton’s first law is often called the law of inertia. Inertia is that tendency of matter to resist a change in its state of rest or state of motion at constant velocity. Mass is a measure of inertia.

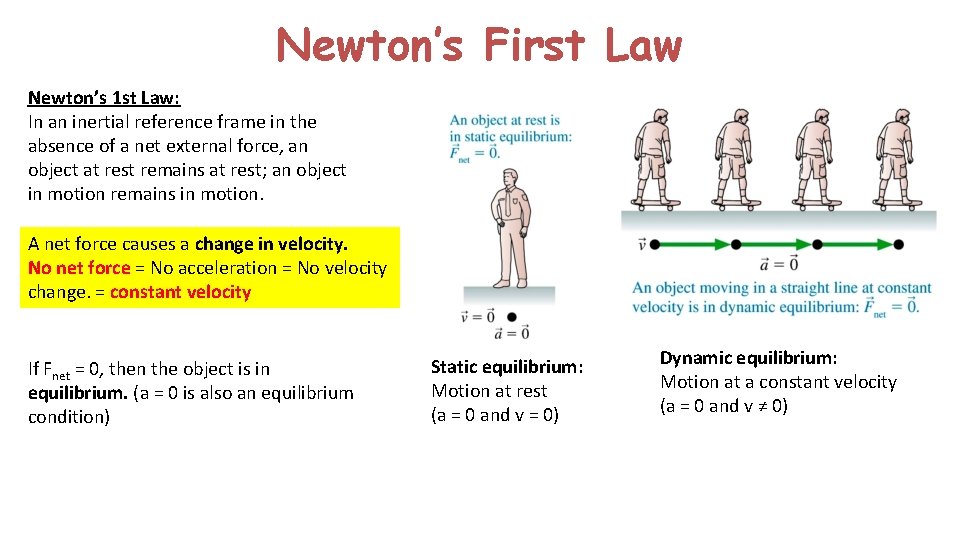
Newton’s First Law Newton’s 1 st Law: In an inertial reference frame in the absence of a net external force, an object at rest remains at rest; an object in motion remains in motion. A net force causes a change in velocity. No net force = No acceleration = No velocity change. = constant velocity If Fnet = 0, then the object is in equilibrium. (a = 0 is also an equilibrium condition) Static equilibrium: Motion at rest (a = 0 and v = 0) Dynamic equilibrium: Motion at a constant velocity (a = 0 and v ≠ 0)

Supertankers illustrate the principal of inertia; their engines are cut off a mile or more before the tanker enters port and it still coasts right on in. In this case, the tanker’s net force is zero, since its velocity does not change! A moving object does not necessarily have a net force on it! There is no “force of motion”!

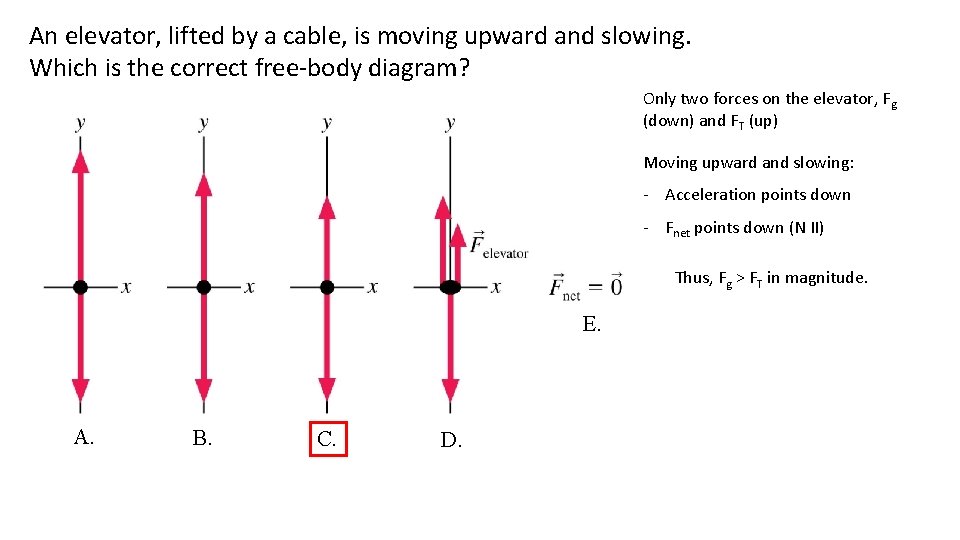
An elevator, lifted by a cable, is moving upward and slowing. Which is the correct free-body diagram? Only two forces on the elevator, Fg (down) and FT (up) Moving upward and slowing: - Acceleration points down - Fnet points down (N II) Thus, Fg > FT in magnitude. E. A. B. C. D.

An object on a rope is lowered at a constant speed. Which is true? A. The rope tension is greater than the object’s weight. B. The rope tension equals the object’s weight. C. The rope tension is less than the object’s weight. D. The rope tension can’t be compared to the object’s weight. Only two forces on the object, Fg (down) and FT (up) Moving downward at a constant speed: - Zero acceleration and thus Fnet = 0 - Forces must be balanced (N I) Thus, Fg = FT in magnitude.

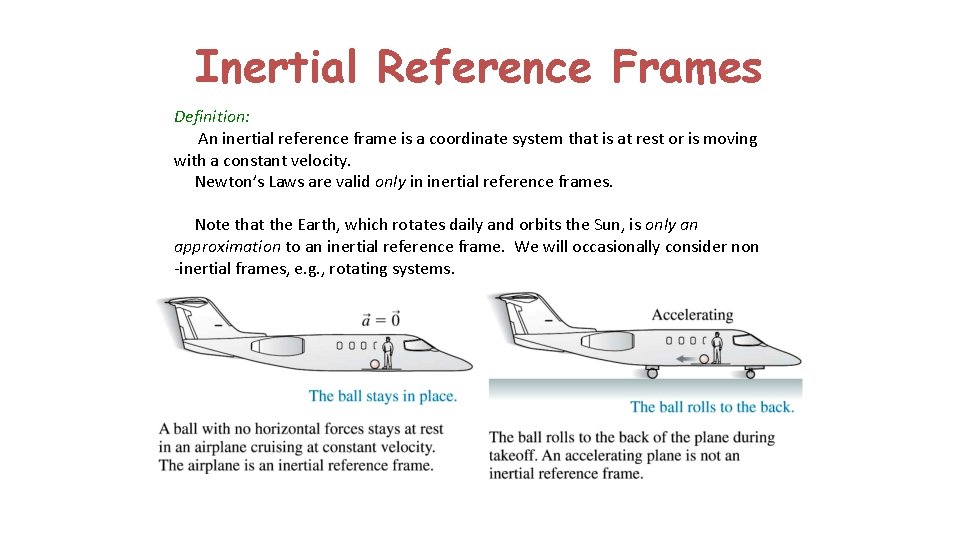
Inertial Reference Frames Definition: An inertial reference frame is a coordinate system that is at rest or is moving with a constant velocity. Newton’s Laws are valid only in inertial reference frames. Note that the Earth, which rotates daily and orbits the Sun, is only an approximation to an inertial reference frame. We will occasionally consider non -inertial frames, e. g. , rotating systems.

Summary: Thinking About Force • Every force has an agent which causes the force. • Forces exist at the point of contact between the agent and the object (except for the few special cases of long-range forces). • Forces exist due to interactions happening now, not due to what happened in the past. Consider a flying arrow. • A pushing force was required to accelerate the arrow as it was shot. • However, no force is needed to keep the arrow moving forward as it flies. • It continues to move because of inertia.