Ch 5 Control Charts for Variables Variablenumerical measurement

Ch 5 Control Charts for Variables Variable：numerical measurement A single measurable quality characteristic, such as a dimension, weight, or volume, is called a variable. C. C. for process average（mean quality）： C. C. for process variability（dispersion）： S chart；R chart（更一般化）. 1

Process mean及Process variability必須同時control. (a) Mean and standard deviation at nomial levels. 2

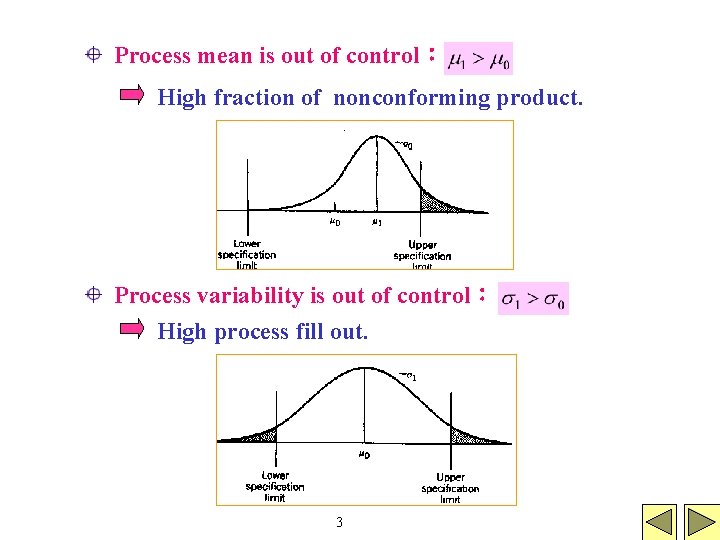
Process mean is out of control： High fraction of nonconforming product. Process variability is out of control： High process fill out. 3

Statistical Basis of the Charts 假設quality characteristic is normally distributed with mean sample and standard deviation . If is a of size n, then the average of this sample is 當X 不是Normal，但n 夠大時，上述之C. L. 亦可使用。 4

若 與 未知時 Center line 其中 每一個都是average of n obs. 從Range估計 Range of （sample of size n） is called the relative range. （sample size n 的函數，查 App. VI） （適用於 5 ） 其中

與 的相對效率 n Relative Efficiency 2 1. 000 3 0. 992 4 0. 975 5 0. 955 6 0. 930 10 0. 850 隨n增大而遞減 For moderate value of n, say , the range loses efficiency rapidly, as it ignores all the information in the sample between and. 結論：exhibit in control. 6

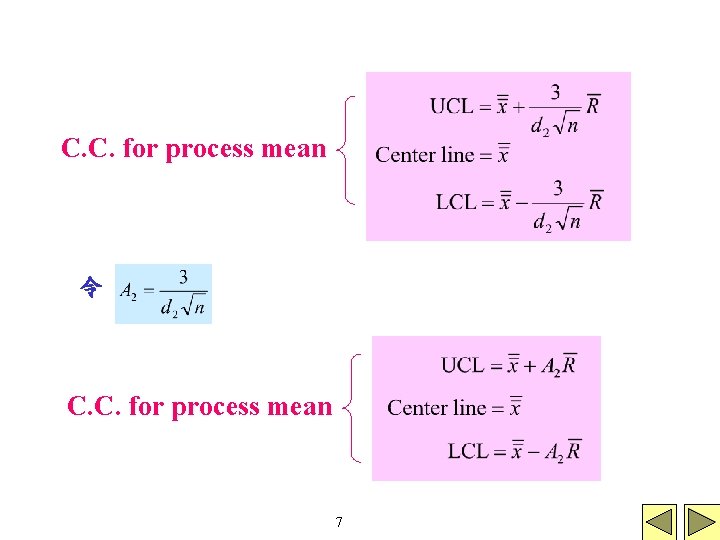
C. C. for process mean 令 C. C. for process mean 7

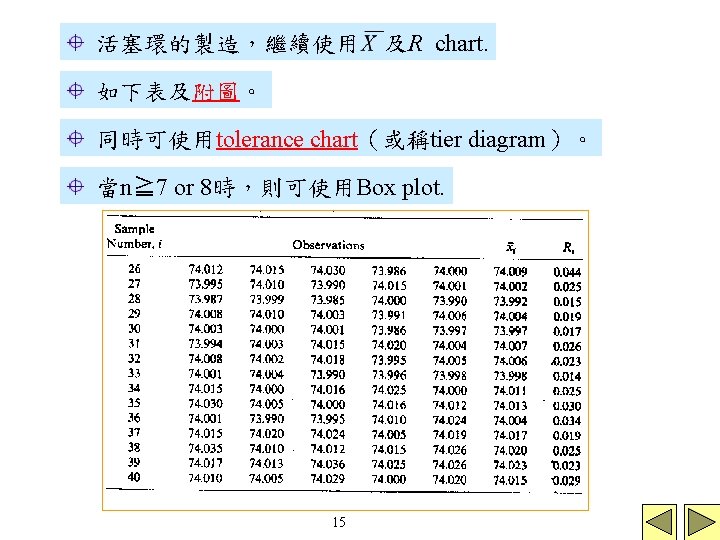
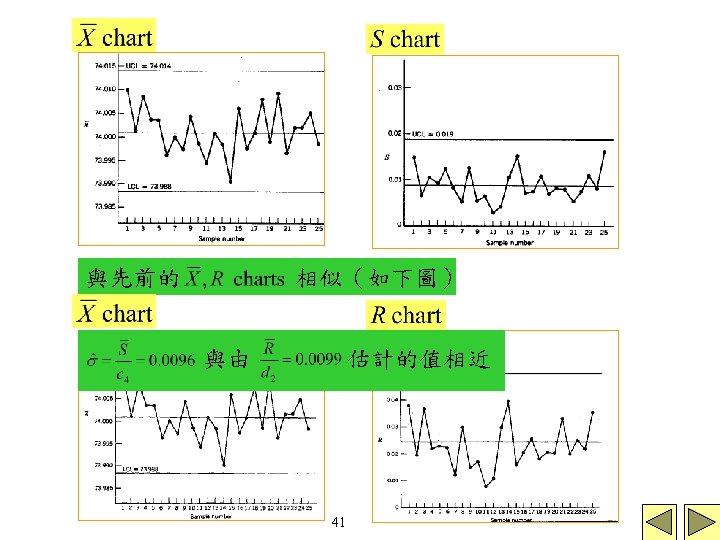
Example 1： 25個samples，每個n=5（見附表） 。Process variability in control （見附圖） 。Process mean in control （見附圖） 結論：Since both and R charts exhibit control, we would conclude that the process is in control at the stated levels and adopt the trial control limits for use in on-line statistical process control. 9

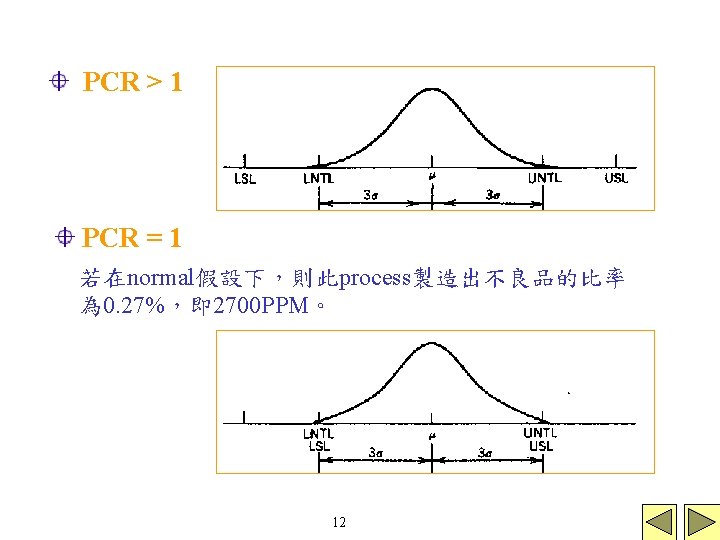
Estimating Process Capability 如何評估製造過程的Capability（能力） 假設活塞環的specification limits是 74 ± 0. 05 mm， 則在上述例子中製造不良活塞環的比率為 PCR（process capability ratio）：另一個評估capability的指標 Specification Process capability的基本定義 10

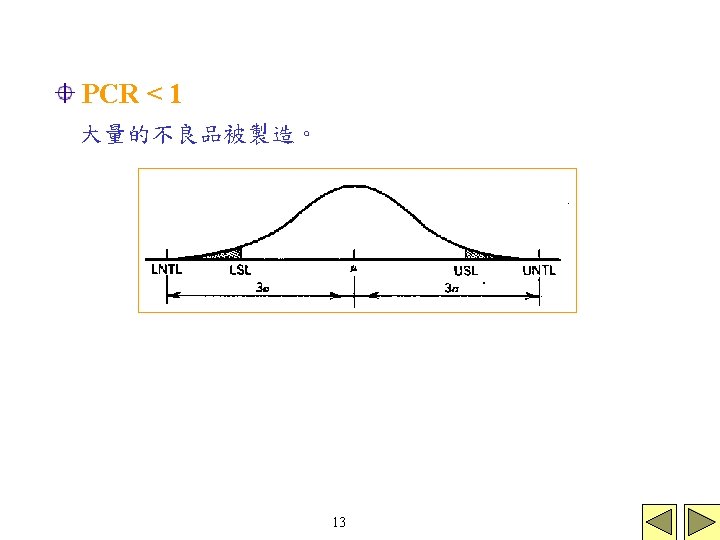
一般 為未知，以 估計，上述中 表示此製造過程的natural tolerance limits是完全落在 USL及LSL之間。 或計算 此process的natural tolerance limits佔據 specification band的60% 11

Revision of Control Limits and Center Lines （定期的修正C. L. 及Center Lines） 例如：每週、每月或每 25、50或 100個樣本。 1. 若R chart顯示in control且process mean僅受單純的 variable控制，則可將center line調到target value， 但若process mean是被更複雜的variables所控制， 則不適宜做此調整。 2. 若R chart顯示out of control，則eliminate那些點再 重新計算center line和control limit。 14

CL 、SL及NTL： CL 與SL兩者之間不存在任何數學關係。 CL是由process的natural variability（即NTL）所決定。 SP則是由management、engineer、customers…決定 （即過程外的因素所決定）。 Control chart使用CL。 Tolerance chart可用specification limits。 16

及R chart rational subgroup的選法 1. 對 chart而言 監測process mean between sample Sample 1 Sample 2 … Maximize the chance for shifts in 2. 對R chart而言 監測process variability within sample 使得variability within samples只測量chance 或random causes 錯誤的估計法！將使S變得太大 且combines了between及within sample的variability. 17

樣本大小 設計C. C. 的準則 CL的寬度 取樣的頻率 CC的統計性質 經濟的考量：cost of sampling, costs of investigating and possibly correcting the process in response to out of control signals, costs associated with producing a product that does not meet specifications. 18

chart若要detect中、大的shift，則n=4、5， 若要detect小的shift，則n=15、25。 small n 可避免shift發生在一個sample之中。 R chart在n小時，對shift相當insensitive。 （e. g. n=5，則detect從 到的機率僅有0. 4。） 但n大時（n≧ 10），則不宜採用R chart，應採用S或 chart。 19

取樣頻率：small, frequent or larger samples less frequently， 目前 業界較偏向於small, frequent的取樣法。 取樣頻率可由rate of production決定。 CL通常取 ，若Type I error甚嚴重，可改採 在短時間內detect出out of control，則可採用 20 ，或需 。

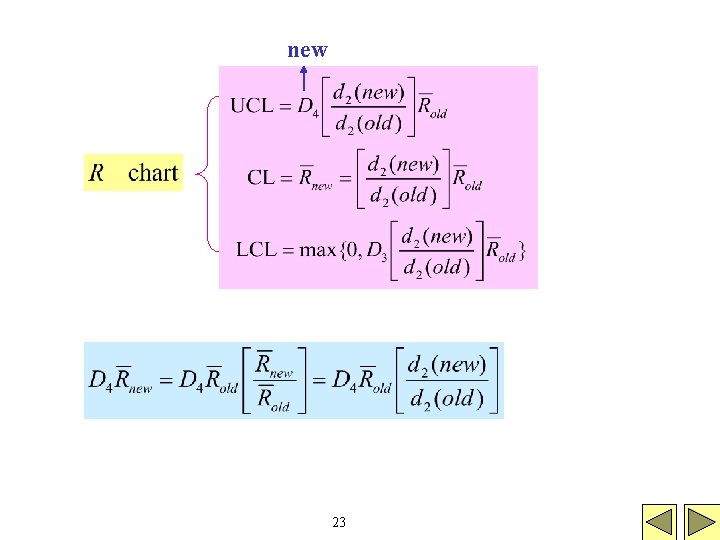
new 23

Example 2：活塞環的製造 由於process exhibits good control ：n↓，CL的寬度↑ （見附圖） ：n↓，center line↓及UCL↓ 24 （見附圖）

Probability Limits on the and R Chart （即由檢定的Type I level所決定的control limit：UK或西歐國家） 1. chart（Normal假設下）： e. g. 2. R chart：由 的percentage points決定。 e. g. If , the 0. 001 and 0. 999 percentage points of the distribution of the relative range W are required. Noting these points by and 當 3≦n≦ 6，有正的LCL 25

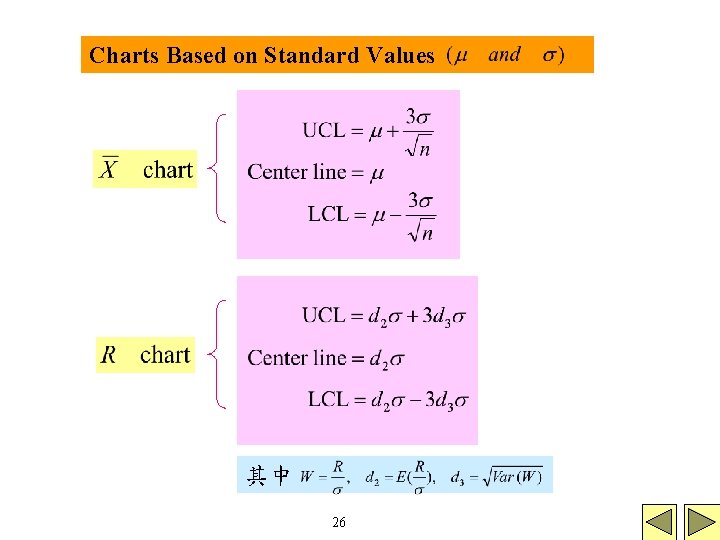
Charts Based on Standard Values 其中 26

使用標準值時，需注意out of control的意義 ！ In processes where the mean of the quality characteristic is controlled by adjustments to the machine, standard or target values of are sometimes helpful in achieving management goals with respect to process performance. 27

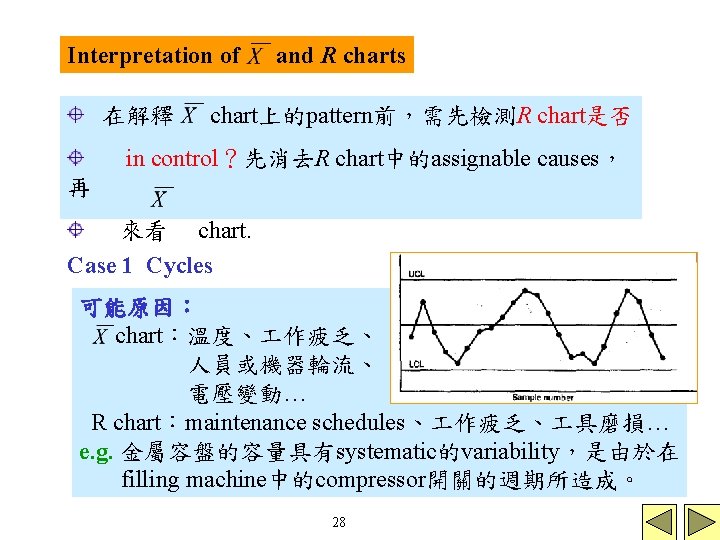
Interpretation of 在解釋 and R charts chart上的pattern前，需先檢測R chart是否 in control？先消去R chart中的assignable causes， 再 來看 chart. Case 1 Cycles 可能原因： chart：溫度、 作疲乏、 人員或機器輪流、 電壓變動… R chart：maintenance schedules、 作疲乏、 具磨損… e. g. 金屬容盤的容量具有systematic的variability，是由於在 filling machine中的compressor開關的週期所造成。 28

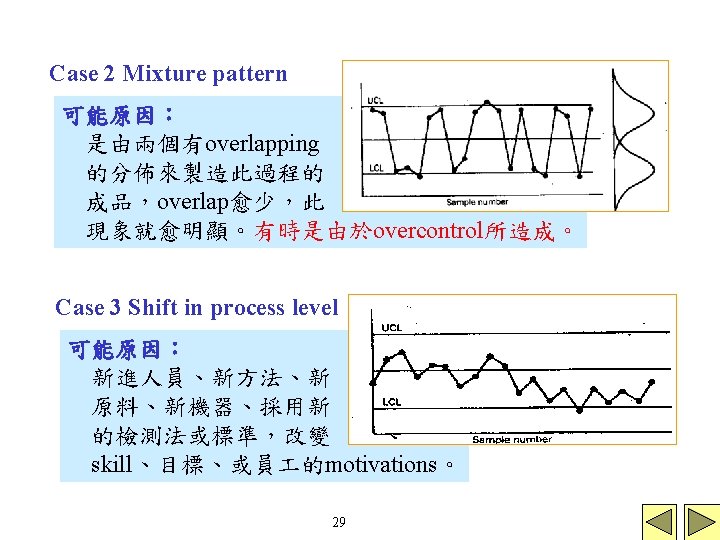
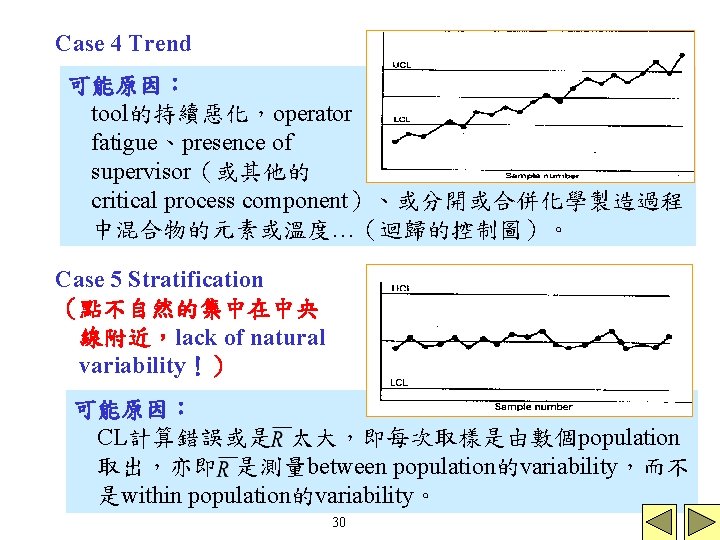
Case 4 Trend 可能原因： tool的持續惡化，operator fatigue、presence of supervisor（或其他的 critical process component）、或分開或合併化學製造過程 中混合物的元素或溫度…（迴歸的控制圖）。 Case 5 Stratification （點不自然的集中在中央 線附近，lack of natural variability！） 可能原因： CL計算錯誤或是 太大，即每次取樣是由數個population 取出，亦即 是測量between population的variability，而不 是within population的variability。 30

E. g. chart：uniform、 right triangular、 gamma（ ）n=4, 5時 robustness 最差的情況：gamma（r=1/2, 1（exponential）) （gamma ） R chart：即使當分佈是normal，R的分佈亦非對稱， 一般使用的 3 -sigma limit，其 （當n=4），且R chart較 sensitive！ 32 chart對normality的假設更

The Operating-Characteristic Function 當 已知時， 當 chart的O. C. curve In control value 的 （如附圖） （在第k個sample（after the shift）才detect出shift的機率） （此即為幾何分佈的期望值） 33

R chart的O. C. curve In control value of the standard deviation 其中 ，查 的表 （如附圖） 利用O. C. curve來分析過去的資料，建議一般取 20~25 subgroups來建立C. C. 。 34

The Average Run Length for the Chart 皆為幾何分佈的期望值 （如附圖） Average Time to Signal： ATS=ARL．k Expected number of individual units sampled： I=n. ARL （如附圖） 35

Control charts for and S 當 1. The sample size n is moderately large, say n>10 or 12. （Recall that the range method for estimating loses statistical efficiency for moderate to large samples. ） 2. The sample size n is variable. 使用 及S charts。 36

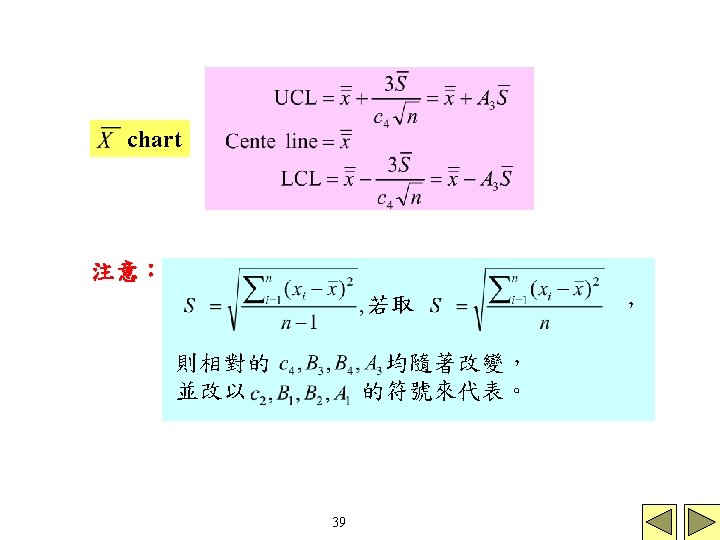
Construction and Operation of 是 的unbiased estimator S並非 的不偏估計量，但 ， 其中 37 and S Charts

當standard value is given S chart 當 是未知，則以 ，估計 S chart 38

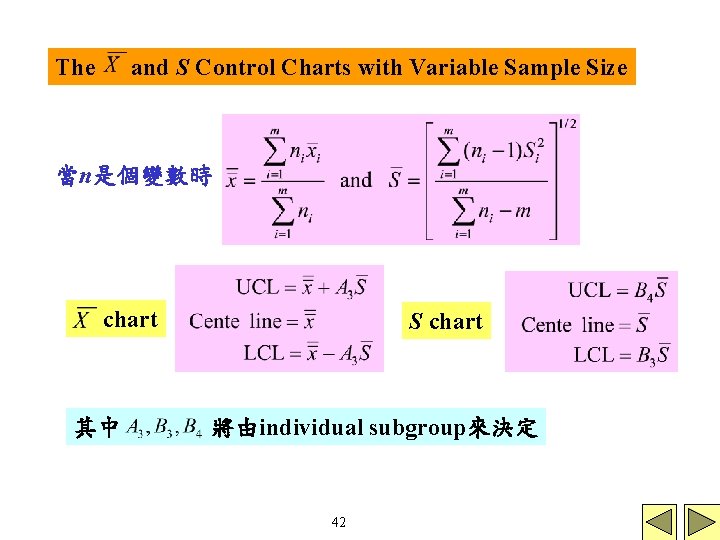
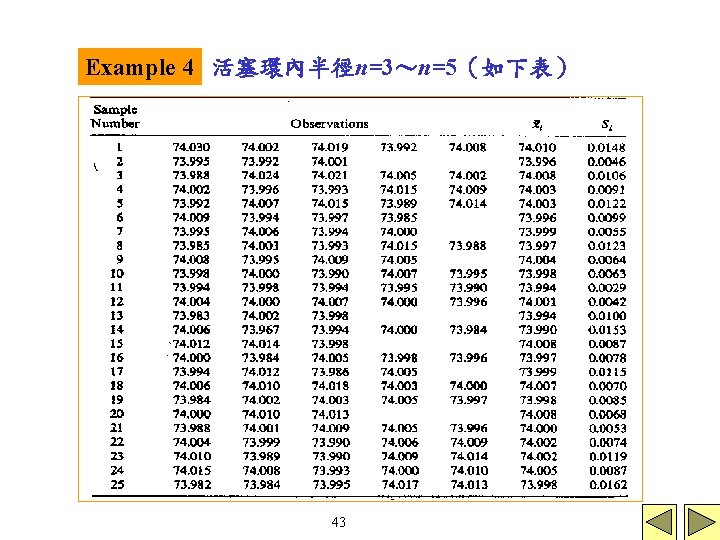
The and S Control Charts with Variable Sample Size 當n是個變數時 chart 其中 S chart 將由individual subgroup來決定 42

The Control Chart（recommended by some practitioners） 46

Control Limits Base on a Small Number of Samples （Short Production Runs） 若無法給定standards，通常以 20~25 preliminary samples 的資料來建立trial control limits，但m=20~25對某些過 程而言卻太大（如start up process）。若m（即sample數） 取得太小，則造成 e. g. chart中， 變大。 即使當m=25時，亦比nominal value大。 解決方法為：Hillier（1969）Two stage approach 來建立C. L. for and R charts. 使得不論m之值為何， 皆可有正確的 值可應用於 job-shop or short production run。 47

可利用相鄰觀測值的moving range來估計process的 variability，即 當要detect的shift很小時，則可採用Ch 7的cumulative sum及exponential weighted moving-average C. C. 。 49

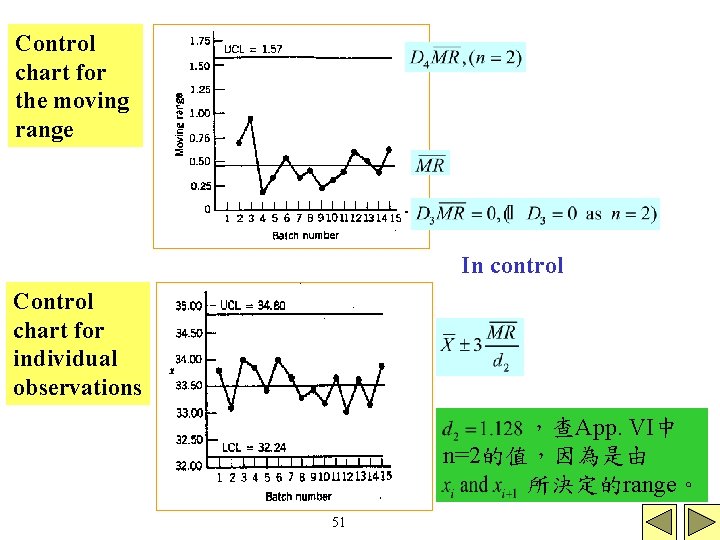
Control chart for the moving range In control Control chart for individual observations ，查App. VI中 n=2的值，因為是由 所決定的range。 51

Crowder發現一般individual及moving range chart的 combined C. C. 的ARL較Shewhart少（亦即pro. of Type I error較大）（=1/0. 0027=370 samples）， 但 若能將moving range chart的 ，其中 D 選在 4≦D≦ 5，則其ARL將會較靠近Shewhart的 in 因而對individual及moving range C. C. 的3 -sigma limit control ARL。 不宜再narrow來提高detect small process shift的能 力， 較可行的方法是採用cumulative sum C. C. 或 exponentially weighted moving-average C. C. 。 53

對individual C. C. 而言，當其不符合normality假設時，可 1. 由其percentiles of underlying distribution來決定control limits。 2. 或transfer variable來使其較靠近Normal分佈後，再建 立C. C. 。 54

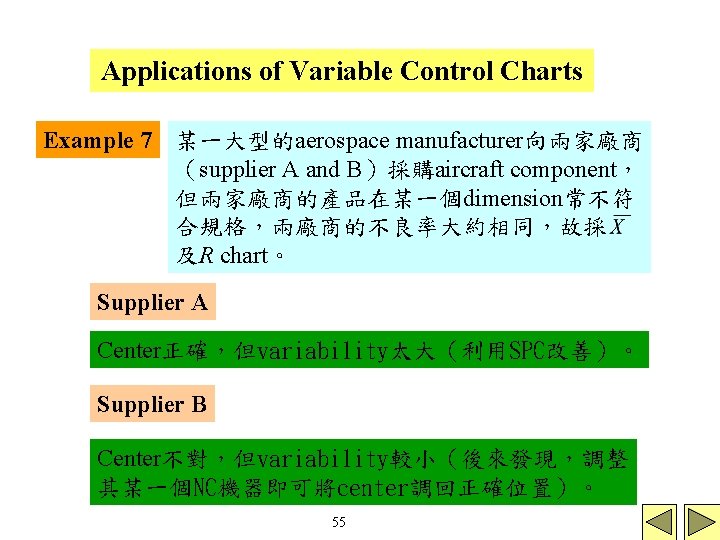
Applications of Variable Control Charts Example 7 某一大型的aerospace manufacturer向兩家廠商 （supplier A and B）採購aircraft component， 但兩家廠商的產品在某一個dimension常不符 合規格，兩廠商的不良率大約相同，故採 及R chart。 Supplier A Center正確，但variability太大（利用SPC改善）。 Supplier B Center不對，但variability較小（後來發現，調整 其某一個NC機器即可將center調回正確位置）。 55

5. chart的使用必須是當between sample的variability 與within sample的variability是一致時，才能使用。 6. 由於S chart是monitor within sample的variability，由 附圖知，大部分均in control；但 chart是monitor between sample的variability。 在此例中，由於rational subgroup的取法使得between sample的variability遠大於within sample的variability （即 ），故在 chart有很多out of control的點。 解決方法：將five vanes的平均高度視為individual measurement，並以moving-range chart來monitor between sample的variability。 結果：S chart + Moving range chart + tolerance chart 效果有顯著改進。 59

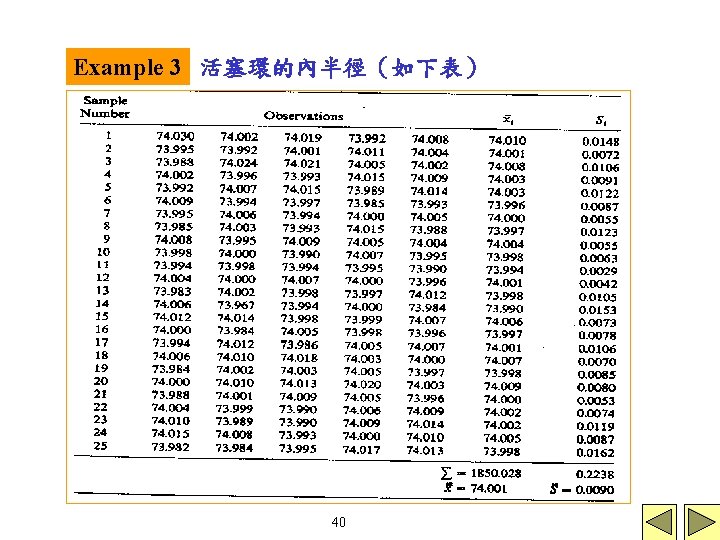
第二個quality characteristic是casting上的opening diameter。 以一個座標測量儀器，測量該opening的直徑 24次（每次 取不同的角度）（i. e. n=24） 同樣在此，傳統的 chart亦不適用，因為between part的 variability遠大於within part的variability。 S chart在此的作用是在測量該part的roundness，若有out of control的點發生，則需檢測製造模的 具（如附圖） 。 60