CH 4 Unsupervised Learning 4 1 Introduction Supervised

CH. 4: Unsupervised Learning 4. 1 Introduction Supervised learning -- learns a mapping from the input to an output using a set of labeled examples Unsupervised learning -- finds the regularities of data using a set of unlabeled examples • Example: Image Segmentation Input image Segmentation 1

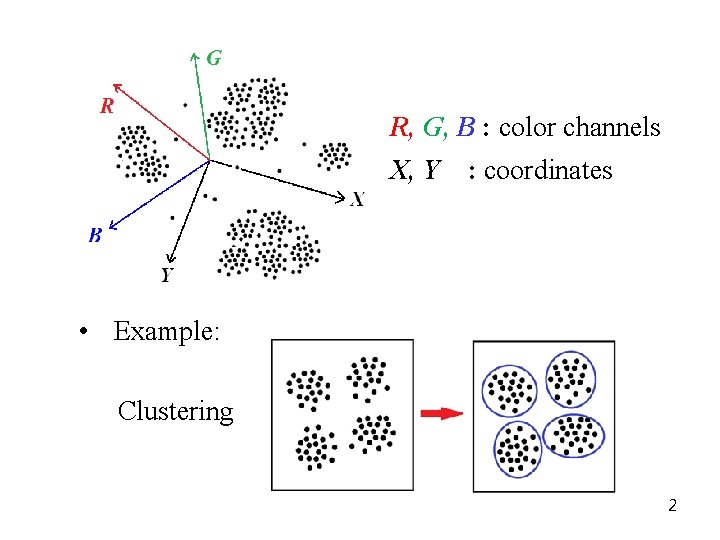
R, G, B : color channels X, Y : coordinates • Example: Clustering 2

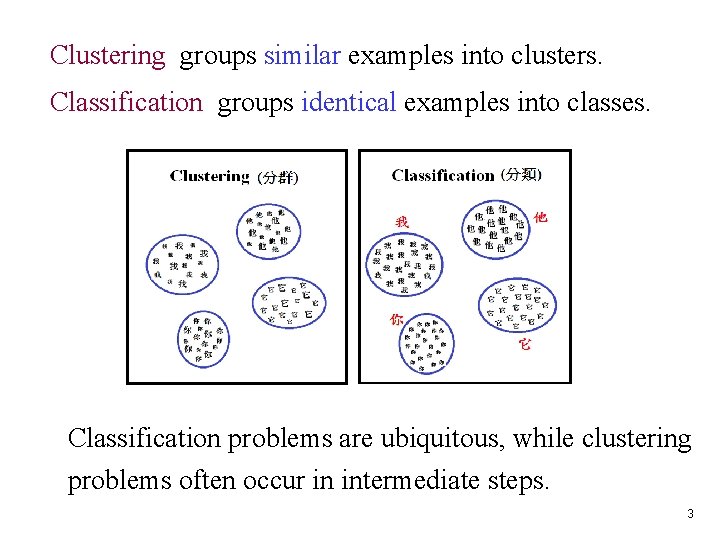
Clustering groups similar examples into clusters. Classification groups identical examples into classes. Classification problems are ubiquitous, while clustering problems often occur in intermediate steps. 3

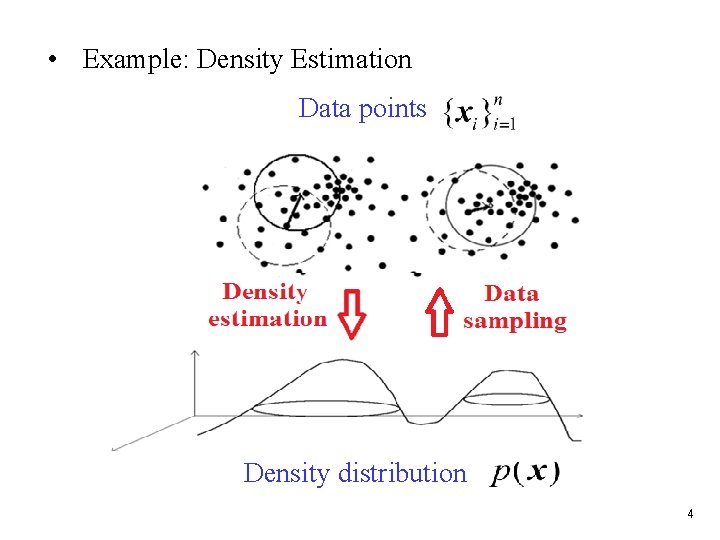
• Example: Density Estimation Data points Density distribution 4

Methods of density estimation: Parametric: The data comes from a single known distribution model , e. g. , . Parameters: Semiparametric: The data consists of many groups, each with a known distribution model. The distribution of data is a mixture of known distribution models, i. e. , Assume Parameters: Nonparametric: No distribution model is known. Parameters: 5

Clustering is an important step in determining #clusters in semiparametric and nonparametric estimations. 6

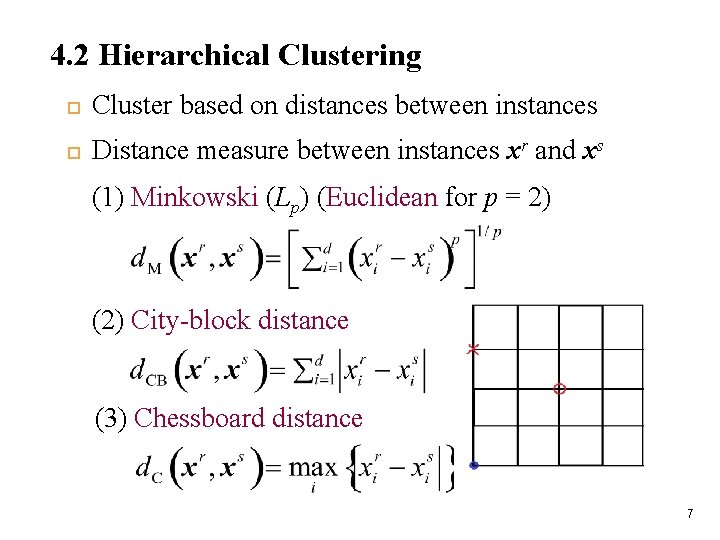
4. 2 Hierarchical Clustering Cluster based on distances between instances Distance measure between instances xr and xs (1) Minkowski (Lp) (Euclidean for p = 2) (2) City-block distance (3) Chessboard distance 7

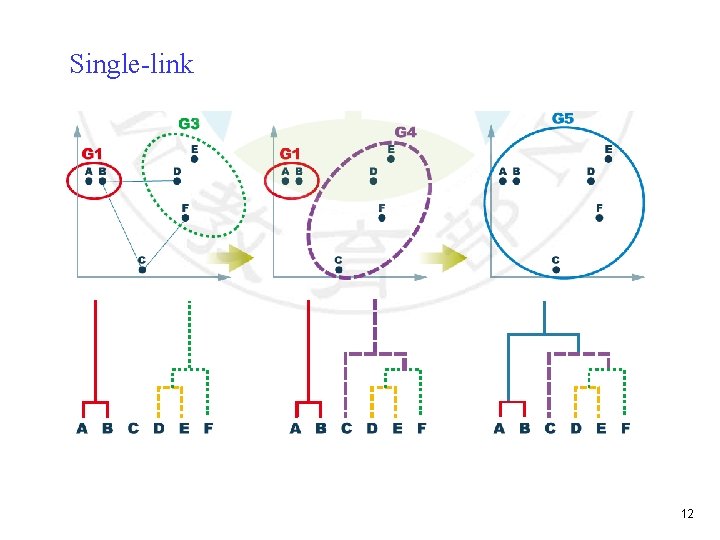
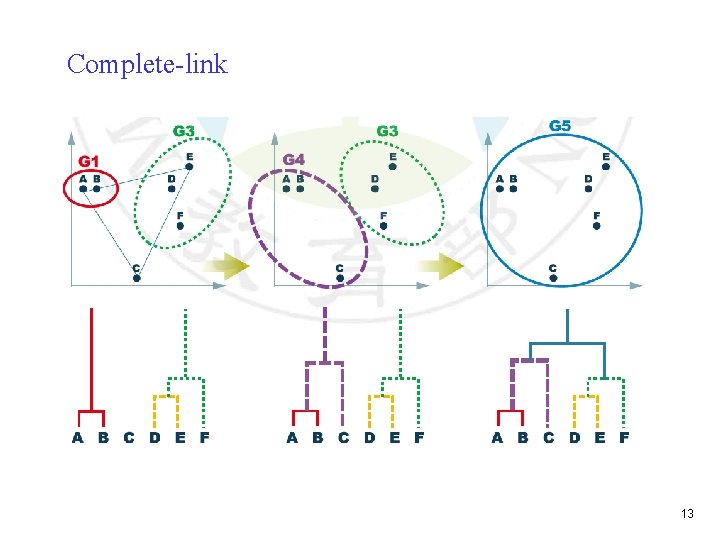
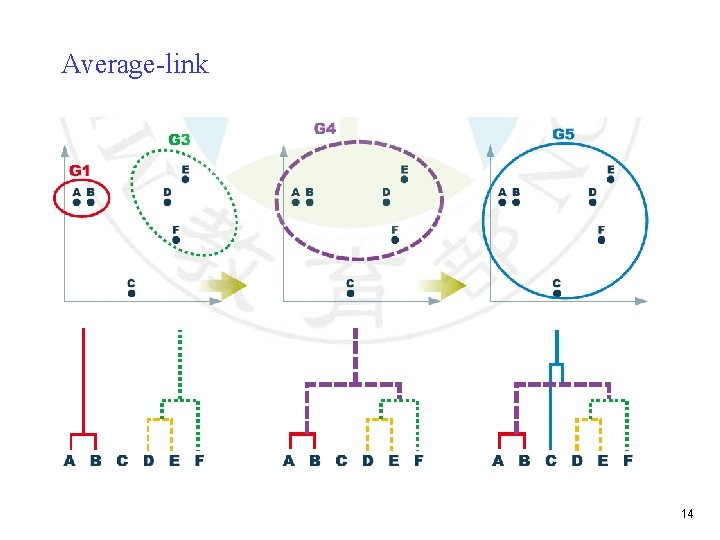
Distance between two groups Gi and Gj: Single-link: Complete-link: Average-link: Centroid distance: the centroids of Gi and Gj 8

Approaches of clustering: (a) Agglomerative Clustering -- Start with N groups each with one instance and merge two closest groups at each iteration until there is a single one. Next, select a threshold to get the clusters. (b) Divisive Clustering -- Start with a single group and dividing large group into two smaller groups, until each group contains a single instance. 9

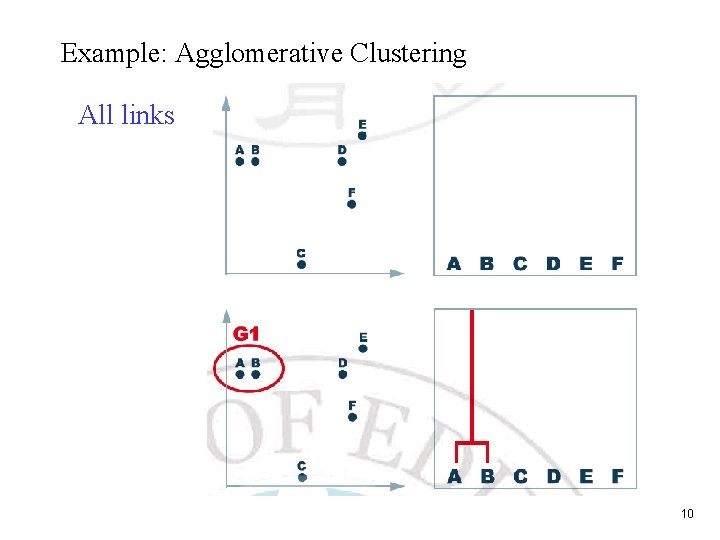
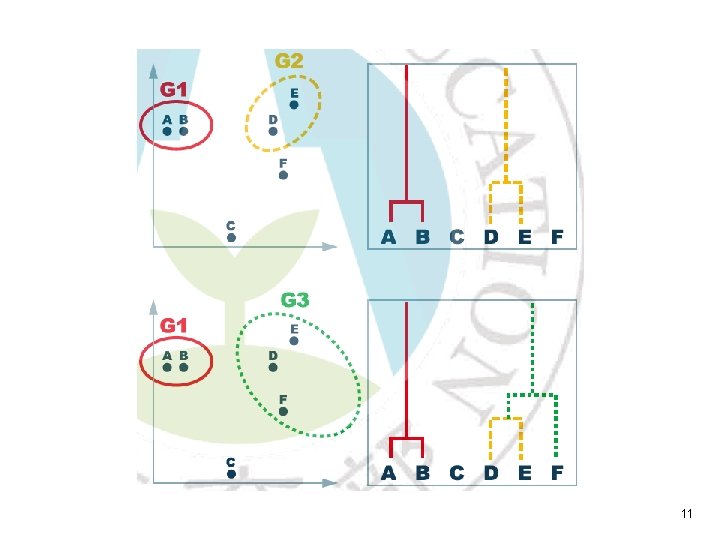
Example: Agglomerative Clustering All links 10

11

Single-link 12

Complete-link 13

Average-link 14

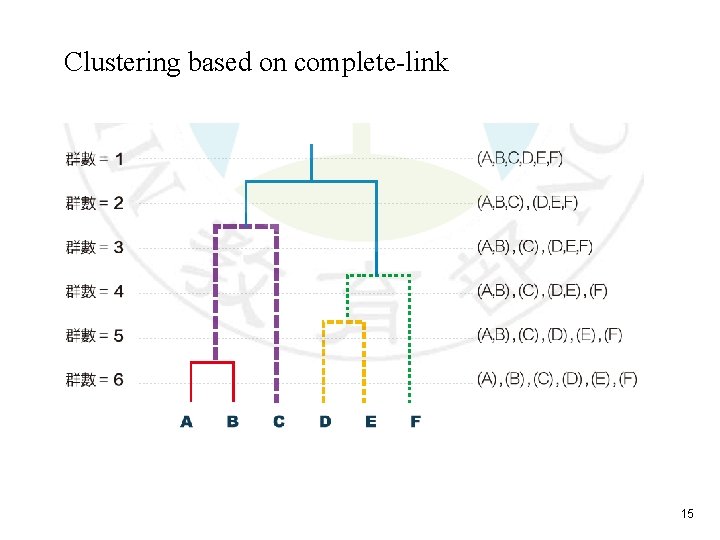
Clustering based on complete-link 15

4. 3 k-Means Clustering Given a sample find the centers and #clusters k, , i = 1, . . , k, of clusters. 16

Methods of initializing 1) Randomly select k well separate examples as the initial . 2) Add to the mean m of data with k small random vectors to get the initial . 3) Calculate the principal component, divide its range into k equal intervals, partition the data into k groups, take the means of these groups as the initial . 17

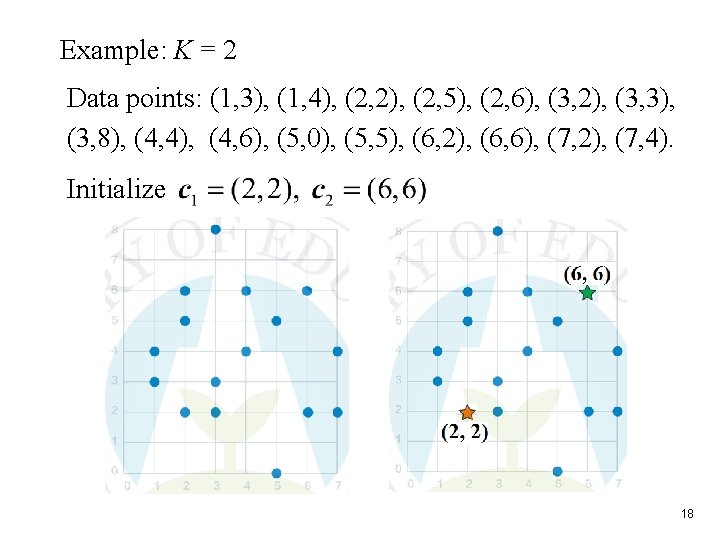
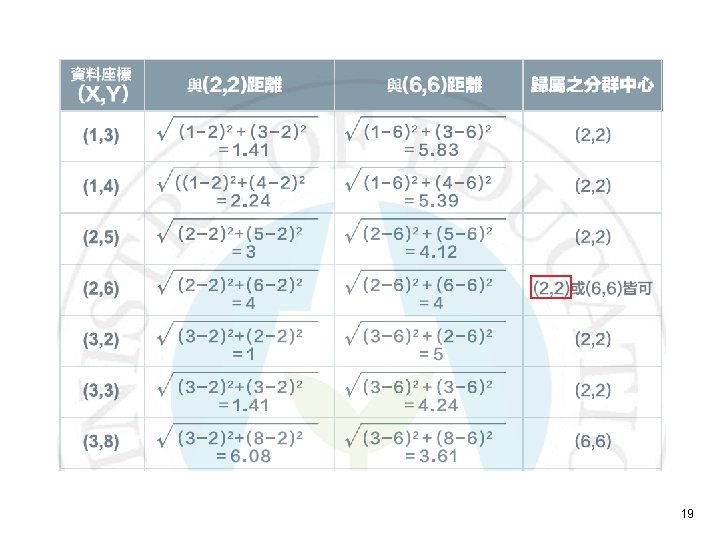
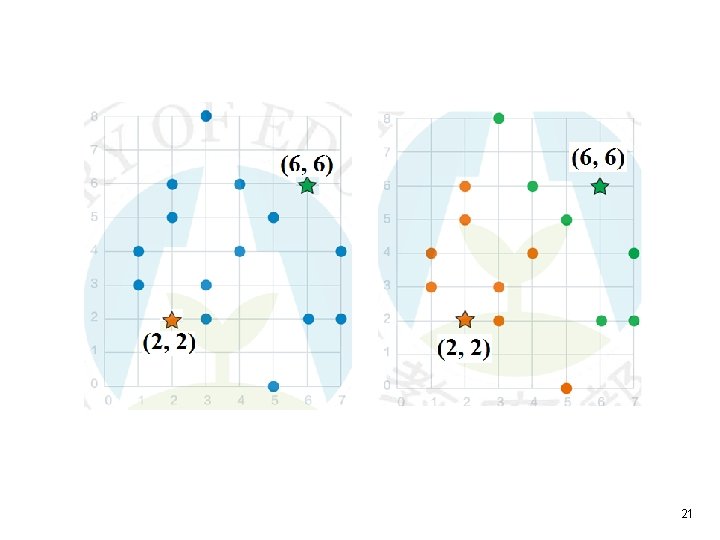
Example: K = 2 Data points: (1, 3), (1, 4), (2, 2), (2, 5), (2, 6), (3, 2), (3, 3), (3, 8), (4, 4), (4, 6), (5, 0), (5, 5), (6, 2), (6, 6), (7, 2), (7, 4). Initialize 18

19

20

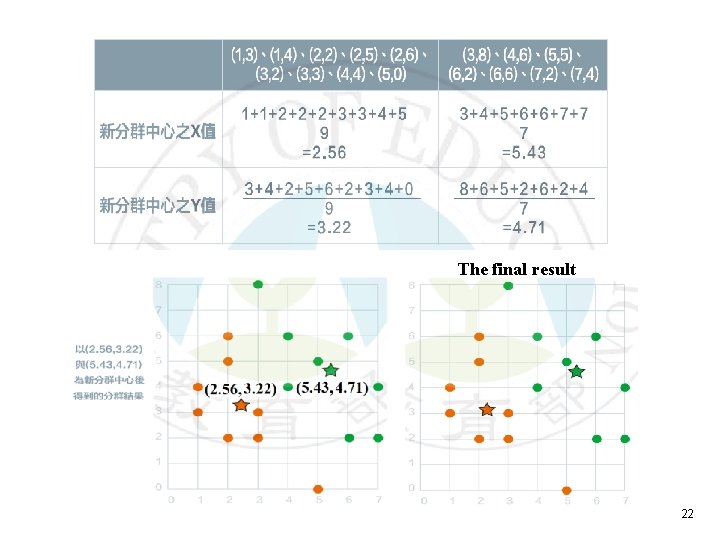
21

The final result 22

Measure of goodness of clustering: Xie-Beni index S: Fukuyama-Sugeno index: Classification entropy index: 23

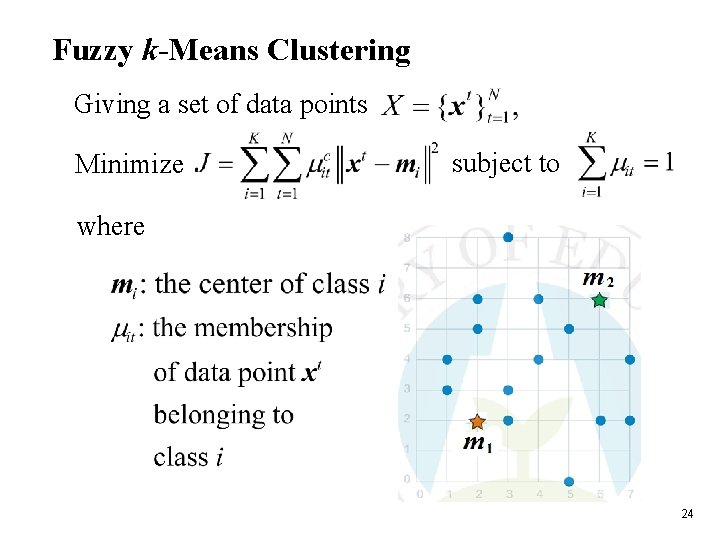
Fuzzy k-Means Clustering Giving a set of data points Minimize subject to where 24

By Lagrange multipliers method Minimize subject to Let 25

Let Steps: 1) Compute according to (B) 2) Compute according to (A) 3) Update 4) If otherwise to obtain by (B), stop go to step 2 26