Ch 4 Review of Basic Probability and Statistics

Ch. 4 Review of Basic Probability and Statistics

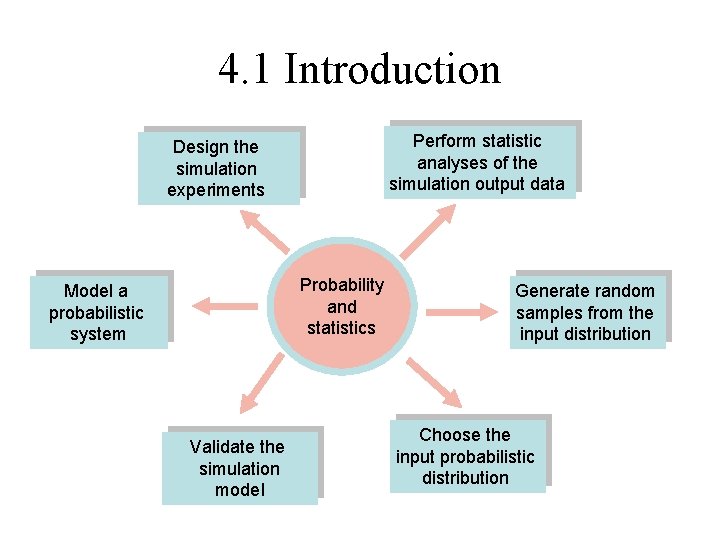
4. 1 Introduction Perform statistic analyses of the simulation output data Design the simulation experiments Probability and statistics Model a probabilistic system Validate the simulation model Generate random samples from the input distribution Choose the input probabilistic distribution

4. 2 Random variables and their properties • Experiment is a process whose outcome is not known with certainty. • Sample space (S) is the set of all possible outcome of an experiment. • Sample points are the outcomes themselves. • Random variable (X, Y, Z) is a function that assigns a real number to each point in the sample space S. • Values x, y, z

Examples • flipping a coin S={H, T} • tossing a die S={1, 2, …, 6} • flipping two coins S={(H, H), (H, T), (T, H), (T, T)} X: the number of heads that occurs • rolling a pair of dice S={(1, 1), (1, 2), …, (6, 6)} X: the sum of the two dice

Distribution (cumulative) function : the probability associated with the event Properties: 1. 2. F(x) is nondecreasing [i. e. , if 3. . ].

Discrete random variable A random variable X is said to be discrete if it can take on at most a countable number of values. The probability that X takes on the value Then Probability mass function on I=[a, b]

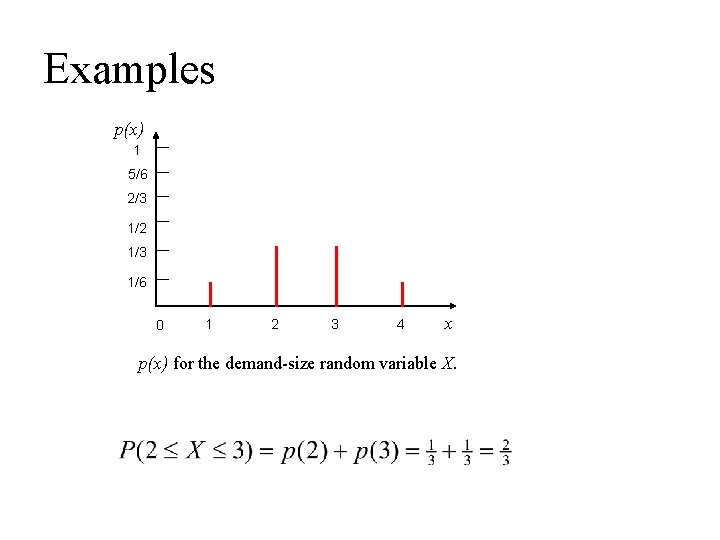
Examples p(x) 1 5/6 2/3 1/2 1/3 1/6 0 1 2 3 4 x p(x) for the demand-size random variable X.

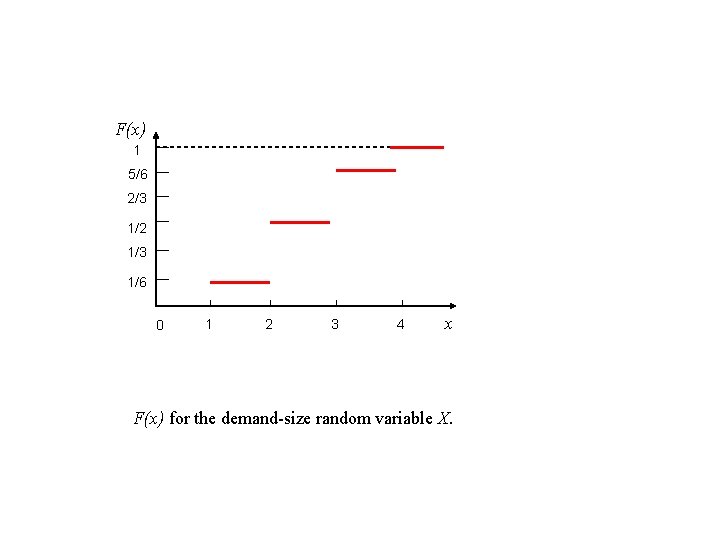
F(x) 1 5/6 2/3 1/2 1/3 1/6 0 1 2 3 4 x F(x) for the demand-size random variable X.

Continuous random variables A random variable is said to be continuous if there exists a nonnegative function f(x) such that for any set of real number B and f(x) is called the probability density function. for all

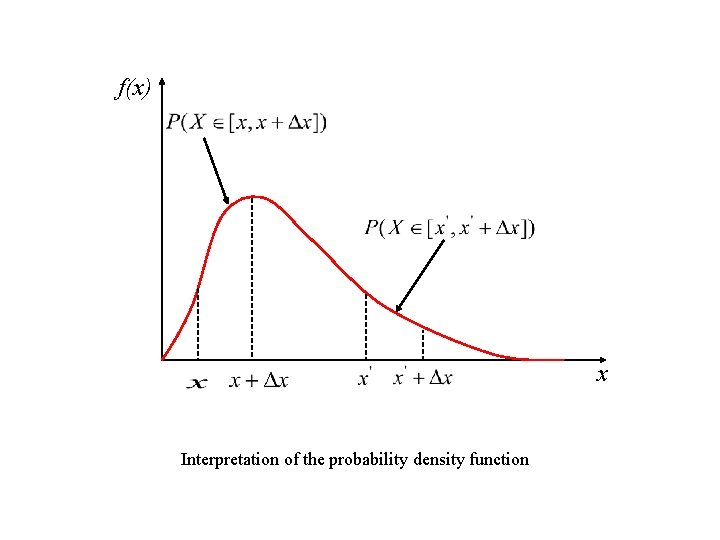
f(x) x Interpretation of the probability density function

Uniform random variable on the interval [0, 1] If , then

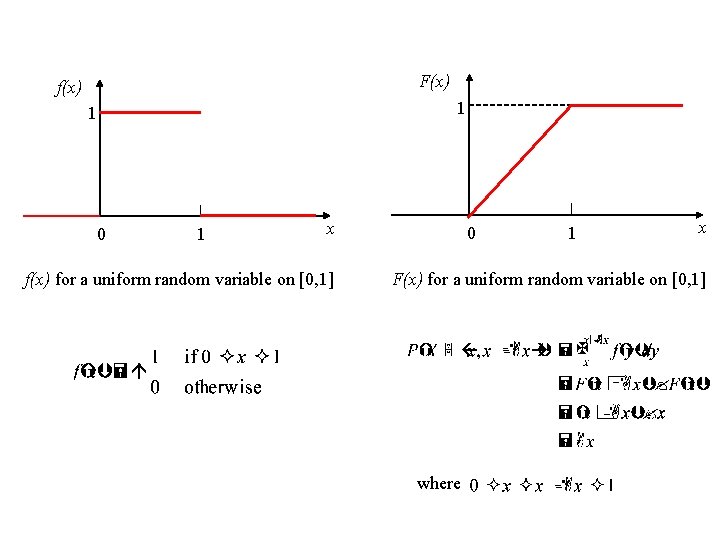
F(x) f(x) 1 1 0 1 x f(x) for a uniform random variable on [0, 1] 0 1 x F(x) for a uniform random variable on [0, 1] where

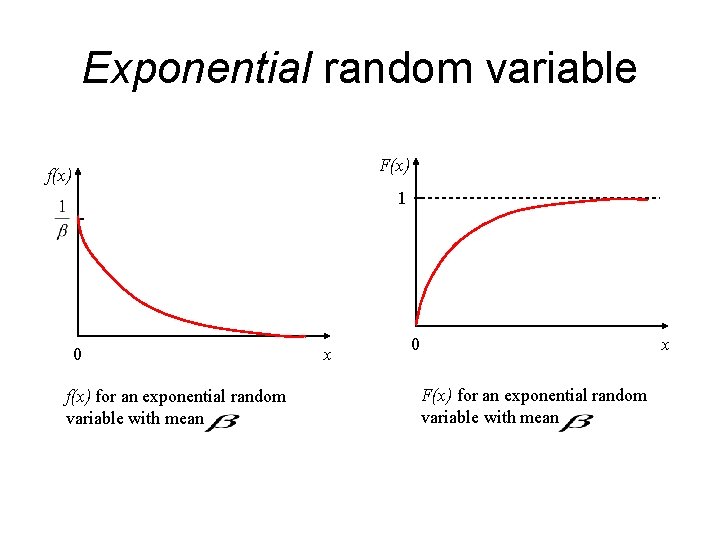
Exponential random variable F(x) f(x) 1 0 f(x) for an exponential random variable with mean x 0 x F(x) for an exponential random variable with mean

Joint probability mass function If X and Y are discrete random variables, then let for all x, y where p(x, y) is called the joint probability mass function of X and Y are independent if for all x, y where are the (marginal) probability mass functions of X and Y.

Example 4. 9 Suppose that X and Y are jointly discrete random variables with Then for x=1, 2 for y=2, 3, 4 Since are independent. For all x, y, the random variables X and Y

Joint probability density function The random variables X and Y are jointly continuous if there exists a nonnegative function f(x, y), such that for all sets of real numbers A and B, X and Y are independent if for all x and y where are the (marginal) probability density functions of X and Y, respectively.

Example 4. 11 Suppose that X and Y are jointly continuous random variables with Then for Since X and Y are not independent.

Mean or expected value The mean is one measure of central tendency in the sense that it is the center of gravity

Examples 4. 12 -4. 13 For the demand-size random variable, the mean is given by For the uniform random variable, the mean is given by

Properties of means 1. 2. Even if the ‘s are dependent.

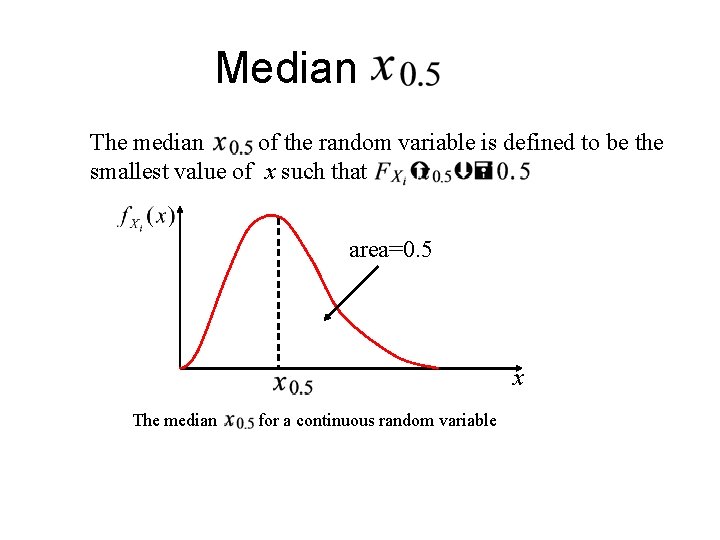
Median The median of the random variable is defined to be the smallest value of x such that area=0. 5 x The median for a continuous random variable

Example 4. 14 1. Consider a discrete random variable X that takes on each of the values, 1, 2, 3, 4, and 5 with probability 0. 2. Clearly, the mean And the median of X are 3. 2. Now consider random variable Y that takes on each of the values, 1, 2, 3, 4, and 100 with probability 0. 2. The mean and the median of X are 22 and 3, respectively. Note that the median is insensitive to this change in the distribution. The median may be a better measure of central tendency than the mean.

Variance For the demand-size random variable, For the uniform random variable on [0, 1],

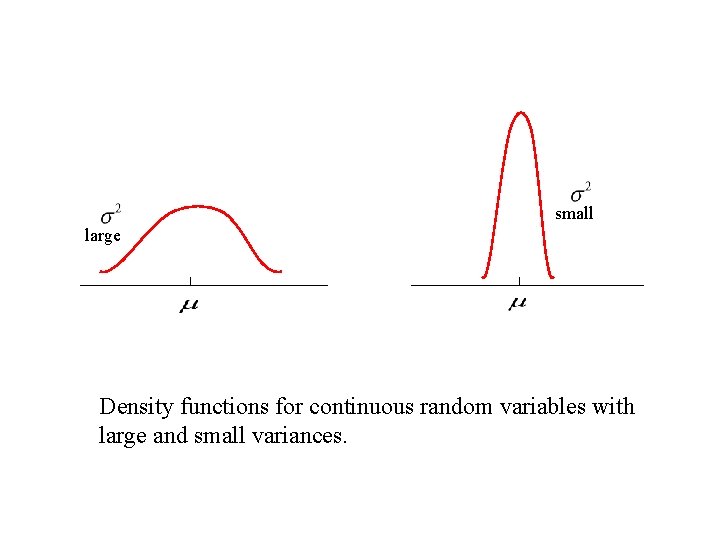
small large Density functions for continuous random variables with large and small variances.

Properties of the variance 1. 2. 3. if the independent (or uncorrelated). ‘s are

Standard deviation The probability that is between and is 0. 95.

Covariance The covariance between the random variables is a measure of their dependence. if i=j, and

Example 4. 17 For the jointly continuous random variables X and Y in Example 4. 11

If and are independent random variables and are uncorrelated. Generally, the converse is not true.

Correlated If If , then and are said to be positively correlated. and tend to occur together , then and are said to be negatively correlated. and tend to occur together

Correlation If is close to +1, then and are highly positively correlated. If is close to -1, then and are highly negatively correlated. For the random variable in Example 4. 11

4. 3 Simulation output data and stochastic processes Stochastic process is a collection of "similar" random variables ordered over time, which are all defined on a common sample space. State space is the set of all possible values that these random variables can take on. Discrete-time stochastic process: Continuous-time stochastic process:

Example 4. 19 M/M/1 queue with IID interarrival times IID service times FIFO service Define the discrete-time stochastic process of delays in queue and are positively correlated. input random variables simulation output stochastic process The state space: the set of nonnegative real numbers

Example 4. 20 For the queueing system of Example 4. 19, Let be the number of customers in the queue at time t. Then is a continuous-time stochastic process with state space

Covariance-stationary Assumptions about the stochastic process are necessary to draw inferences in practice. A discrete-time stochastic process is said to be covariance-stationary, if and is independent of i for

Covariance-stationary process For a covariance-stationary process, the mean and variance are stationary over time, and the covariance between two observations and depends only on the separation j and not actual time value i and i+j. We denote the covariance and correlation between and respectively, where and by

Example 4. 22 Consider the output process M/M/1 queue with for a covariance-stationary.

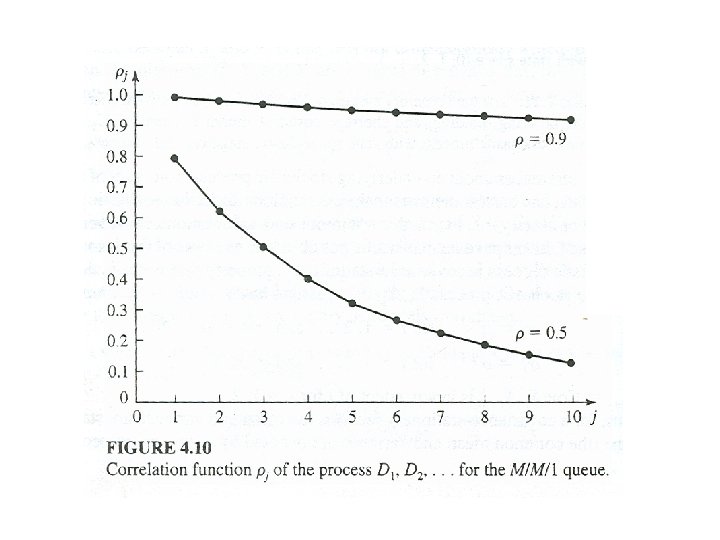
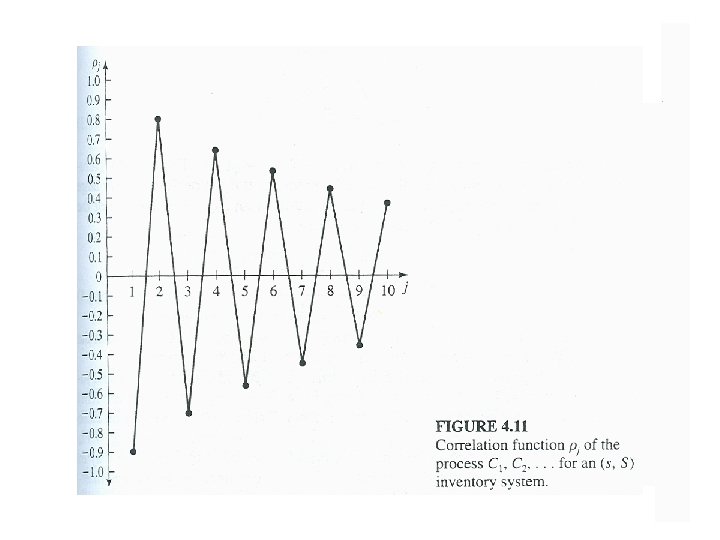
Warmup period In general, output processes for queueing systems are positively correlated. If is a stochastic process beginning at time 0 in a simulation, then it is quite likely not to be covariancestationary. However, for some simulation will be approximately covariance-stationary if k is large enough, where k is the length of the warmup period.

4. 4 Estimation of means, variance, and correlations Suppose population mean Unbiased estimators: Sample mean Sample variance are IID random variables with finite and finite population variance

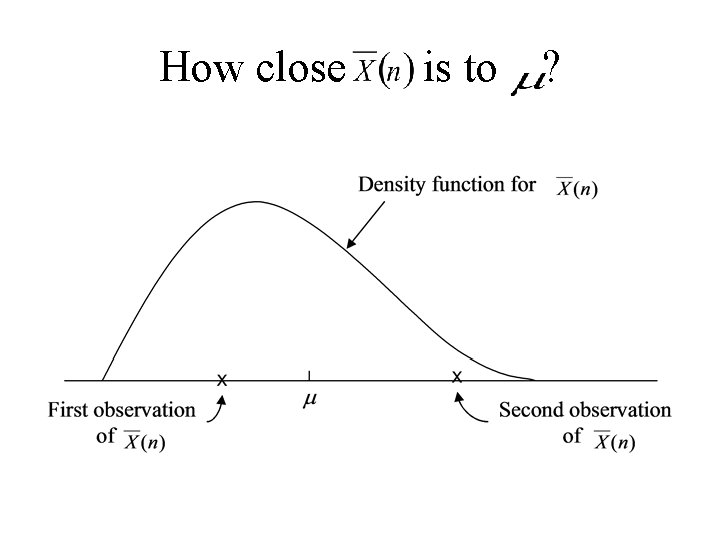
How close is to ?

How close to construct a confidence interval Unbiased estimator is to

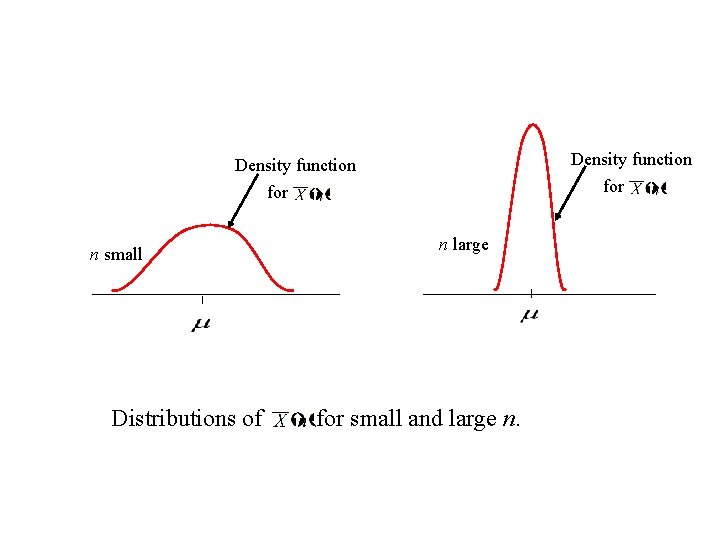
Density function for n small Distributions of n large for small and large n.

Estimate the variance of the sample mean. ´s are independent ´s are uncorrelated However, the simulation output data are almost always correlated. are from a covariance-stationary stochastic process, Then, is an unbiased estimator of , however, is no longer an unbiased estimator of. Since

However, simulation output data are always correlated. Since (1) For a covariance-stationary process: (2)

If one estimates from (correct in the IID case) there are two errors: • the bias in as an estimator of. • the negligence of the correlation terms in Eq. (2). Solution: combine Eq. (1) and Eq. (2) (3) If , then and .

Example 4. 24 from the process of delays for a covariancestationary M/M/1 queue with. Eq. (1) and (3) Thus, is a gross underestimate of likely to be overly optimistic about the closeness of , and we are to

Estimate . In general "good" estimates of the 's will be difficult to obtain unless n is very large and j is small relative to n.

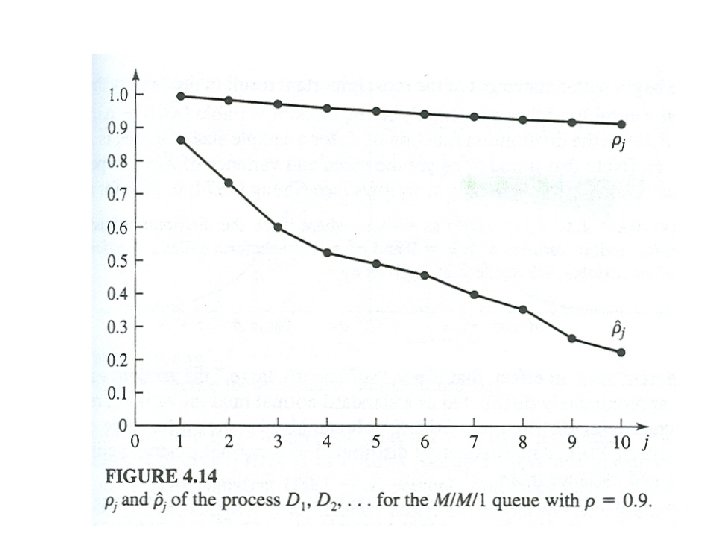
4. 5. 1 Confidence Intervals

4. 5. 1 Confidence Intervals Central Limit Theorem: as , where the distribution function of a normal random variable with and , is given by , If n is "sufficiently large", the random variable will be approximately distributed as a standard normal random variable, regardless of the underlying distribution of the 's. For large n, the sample mean is approximately distributed as a normal random variable with mean and variance

where ( ) is the upper a standard normal random variable. critical point for

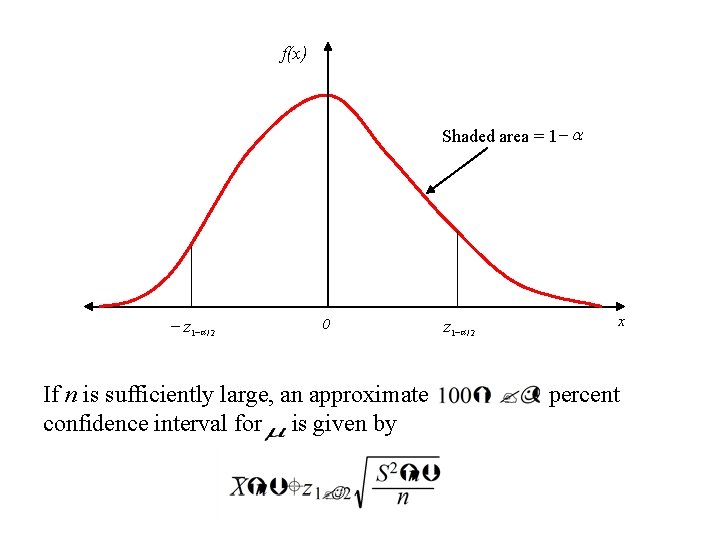
f(x) Shaded area = 1 - a - z 1 -a / 2 0 If n is sufficiently large, an approximate confidence interval for is given by z 1 -a / 2 x percent

Interpretation I: If one constructs a very large number of independent percent confidence intervals, each based on n observations, where n is sufficiently large, the proportion of these confidence intervals that contains (cover) should be. Interpretation II: If the 's are normal random variables, the random variable has a t distribution with n-1 degree of freedom (df), and an exact (for any ) percent confidence interval for is given by Where is the upper distribution with n-1 df critical point for the t

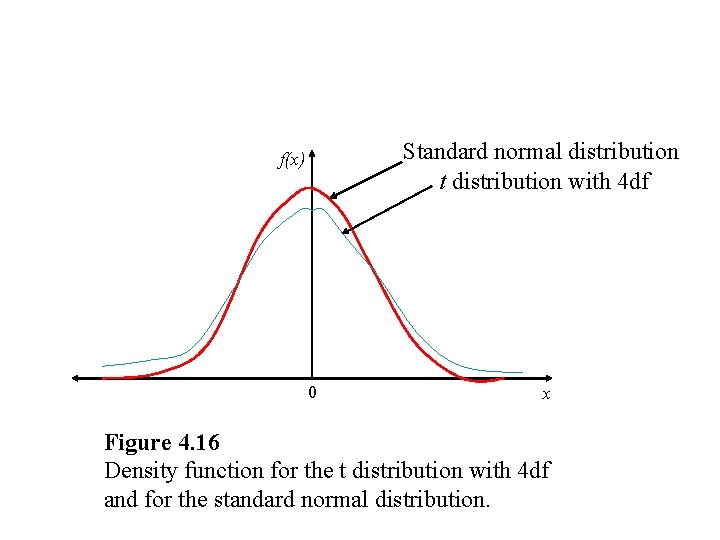
Standard normal distribution t distribution with 4 df f(x) 0 x Figure 4. 16 Density function for the t distribution with 4 df and for the standard normal distribution.

Example 4. 26 10 observations: 1. 20, 1. 50, 1. 68, 1. 89, 0. 95, 1. 49, 1. 58, 1. 55, 0. 50, 1. 09 are from a normal distribution, To construct a 90% confidence interval for .

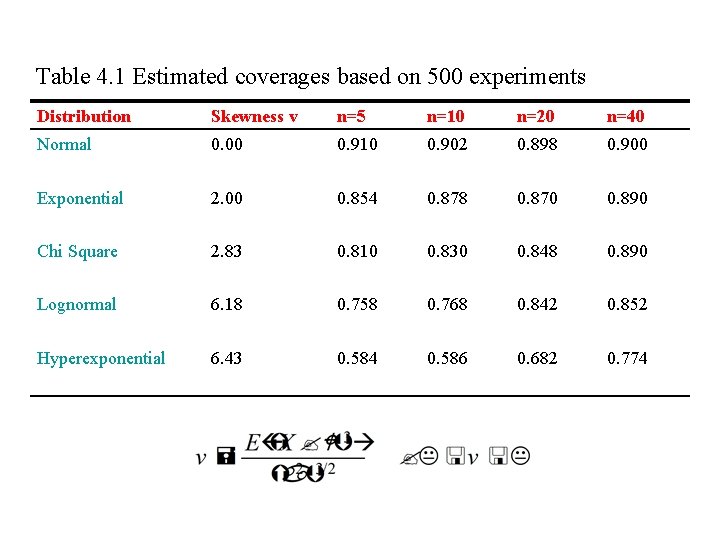
Table 4. 1 Estimated coverages based on 500 experiments Distribution Skewness v n=5 n=10 n=20 n=40 Normal 0. 00 0. 910 0. 902 0. 898 0. 900 Exponential 2. 00 0. 854 0. 878 0. 870 0. 890 Chi Square 2. 83 0. 810 0. 830 0. 848 0. 890 Lognormal 6. 18 0. 758 0. 768 0. 842 0. 852 Hyperexponential 6. 43 0. 584 0. 586 0. 682 0. 774

4. 5. 2 Hypothesis tests for the mean : If is large, is not likely to be true. If is true, the statistic have a t distribution with n-1 df. will

Example 4. 27 For Example 4. 26, To test the null hypothesis We reject . that at level .

4. 6 The Strong Law of Large Numbers Theorem 4. 2

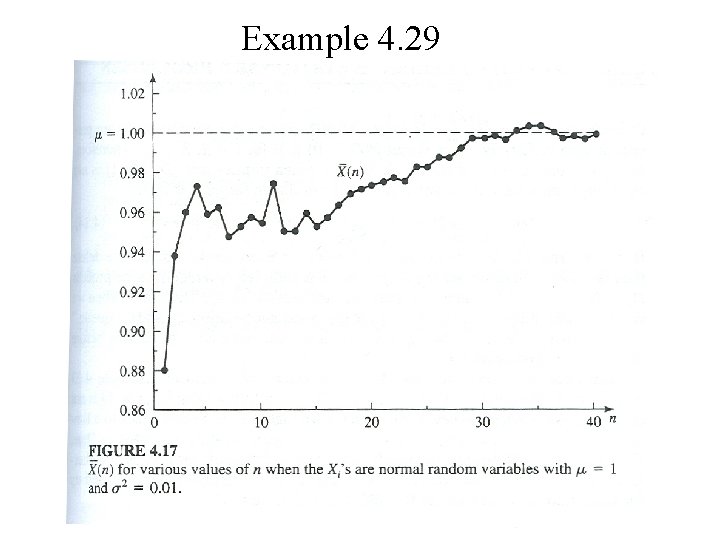
Example 4. 29

Tarea II: Teoría de la probabilitad y estatística A. M. Law and W. D. Kelton, Simulation, Modeling and Analysis, 3 rd edition, pp. 261 -263. Problems 4. 1, 4. 2, 4. 4, 4. 7, 4. 9, 4. 10, 4. 13, 4. 20, 4. 21, 4. 23, 4. 24, 4. 25, 4. 26