Ch 4 RadiometryMeasuring Light Preview The intensity of









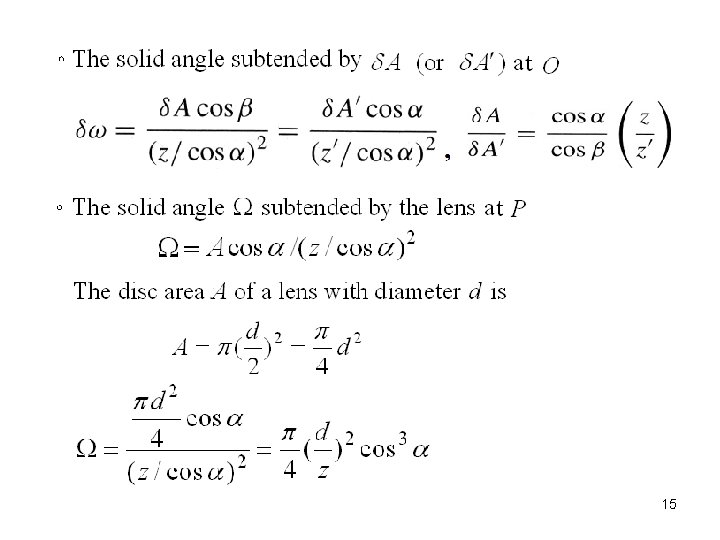















- Slides: 31

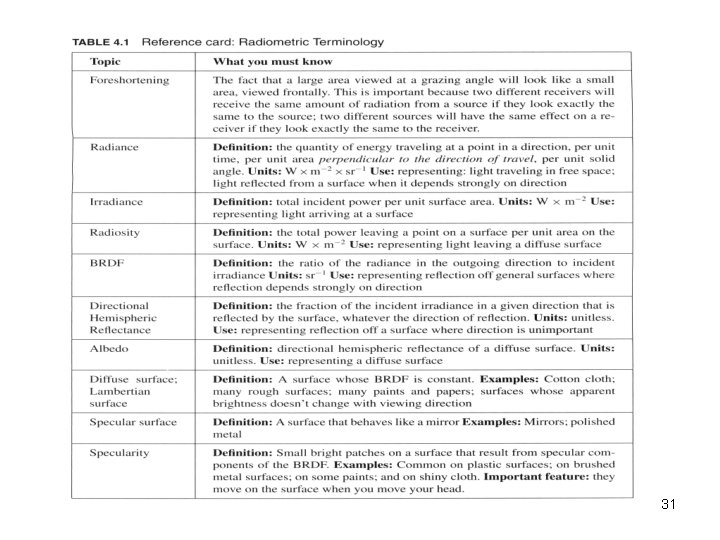
Ch. 4: Radiometry–Measuring Light Preview 。 The intensity of an image reflects the brightness of a scene, which in turn is determined by (a) the amount of light incident on the scene (b) the characteristic of the scene, and 。 An image I is hence often modeled as , where R: reflectance component L: illumination component R typically remains constant to changes of environmental conditions. 1

。 Separating R and L is critical in many applications. Shadow removal Highlight removal Reflection removal 2

However, image decomposition is an ill-posed problem. Additional information is required. To this end, understanding the behavior of light is important. 4. 1 Light in Space ○ Radiometry: Studies the behavior (or measurement) of light, including (a) How energy is transferred from a light source to a surface (b) What happens to the energy when it arrives at a surface. 3

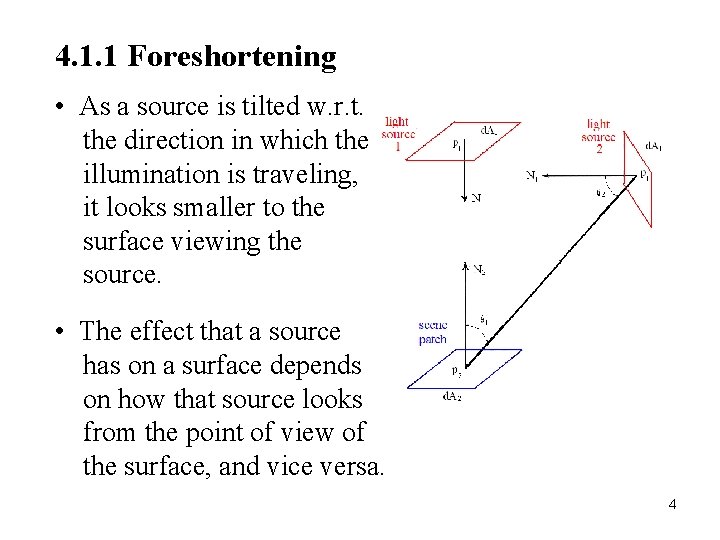
4. 1. 1 Foreshortening • As a source is tilted w. r. t. the direction in which the illumination is traveling, it looks smaller to the surface viewing the source. • The effect that a source has on a surface depends on how that source looks from the point of view of the surface, and vice versa. 4

○ Hemisphere of directions (for a surface point): (a) A surface point sees the world along a hemisphere of directions centered at the point (b) The brightness of the point is computed by summing effects of all incoming directions 5

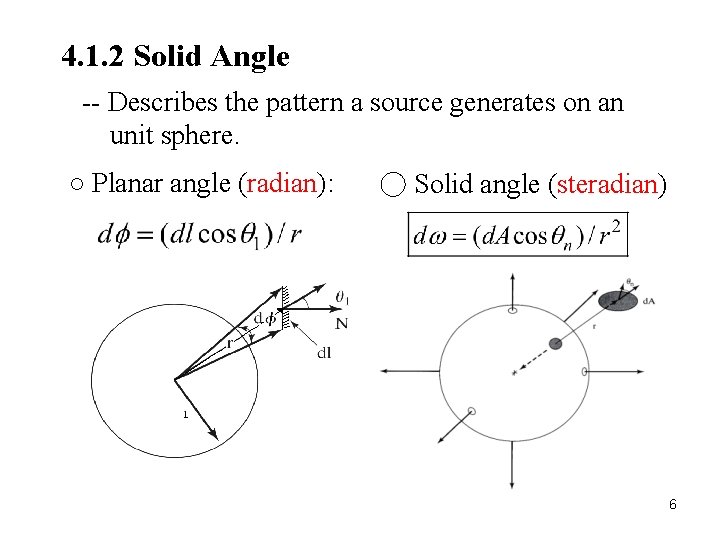
4. 1. 2 Solid Angle -- Describes the pattern a source generates on an unit sphere. ○ Planar angle (radian): ○ Solid angle (steradian) 6

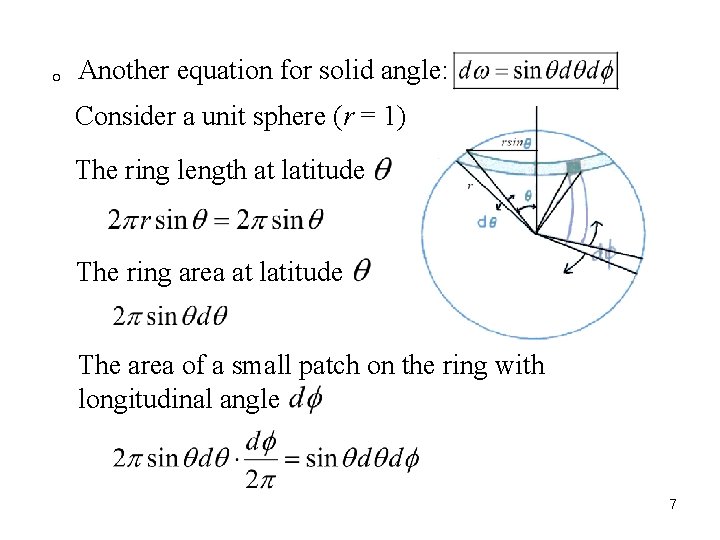
。Another equation for solid angle: Consider a unit sphere (r = 1) The ring length at latitude The ring area at latitude The area of a small patch on the ring with longitudinal angle 7

4. 1. 3 Radiance (unit: ) Radiance -- The amount of energy in direction , per unit time, per unit solid angle, per unit area, from point P 8

4. 1. 4 Irradiance -- The amount of incident energy at point (P) in direction , per unit time, per unit area 。 The incoming power incident on a surface at a point is computed by summing the irradiance over the input hemisphere. 9

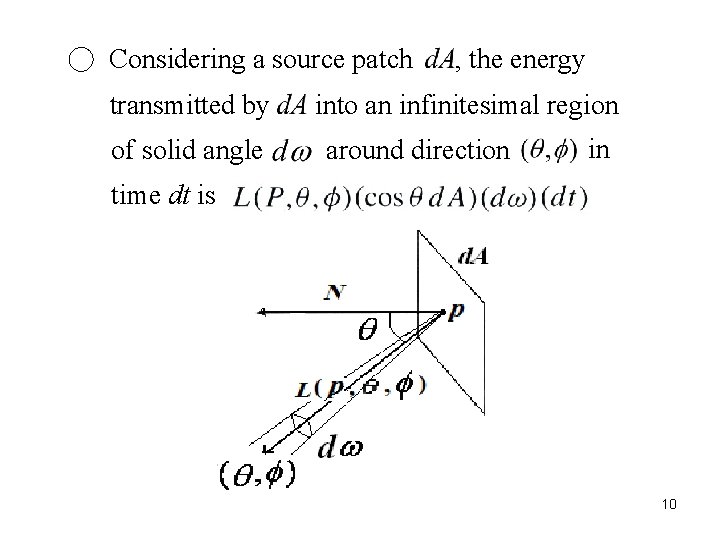
○ Considering a source patch transmitted by of solid angle , the energy into an infinitesimal region around direction in time dt is 10

○ Consider patches, Let leaving : the radiance in the direction of In time dt, the energy leaving for is where subtended by is the solid angle at 11

Let : the irradiance arriving in the direction of where subtended by The energy arriving Substitute is the solid angle at from is into the above equation 12

Energy is constant along straight light, i. e. , The energy leaving in direction of is the same as the energy arriving from direction of 13

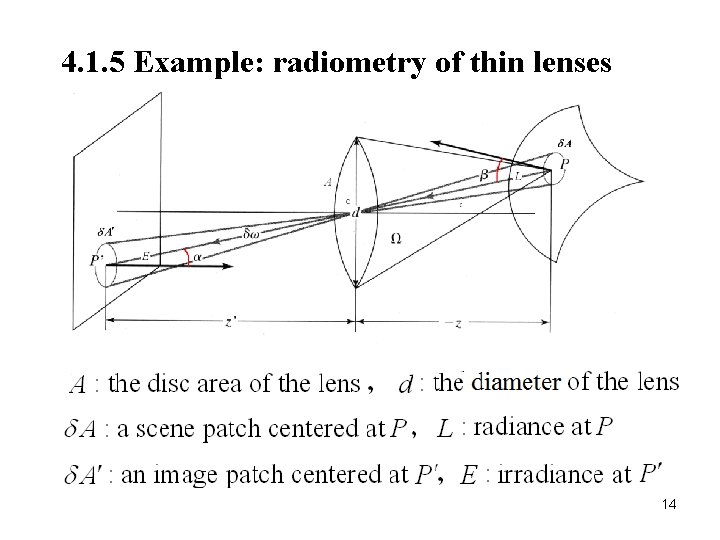
4. 1. 5 Example: radiometry of thin lenses 14
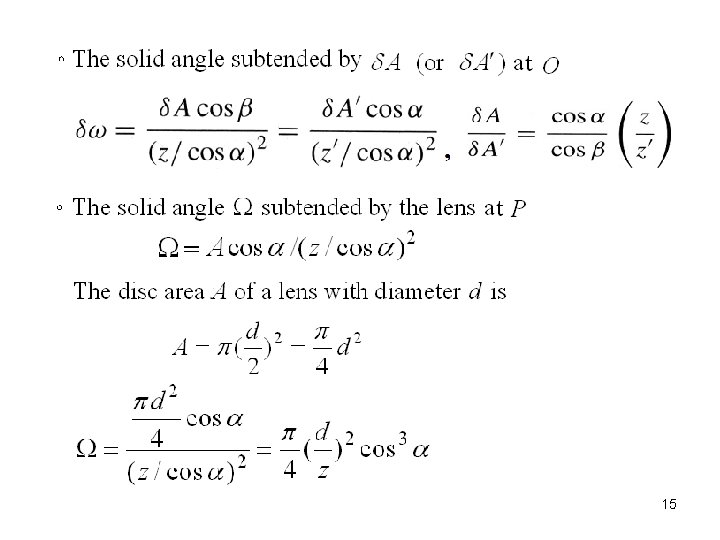
15

16

(e) Image irradiance E is irrelevant to the distance z between the center of the lens and the scene patch 17

18

4. 2. 1 Bidirectional Reflectance Distribution Function (BRDF) -- Defined as the ratio of the outgoing radiance in to the incoming irradiance in * depends on both directions and 19

。 The radiance leaving a surface in due to its irradiance (from all directions): 20

21

22

23

24

25

26

27

28

29

30

31