Ch 4 Chemical Quantities and Aqueous Reaction Stoichiometry

Ch. 4: Chemical Quantities and Aqueous Reaction Stoichiometry: Mole Method Calculations Coefficients in balanced equations give the ratio by moles!!! 2 C 4 H 10 + 13 O 2 e. g. in the above reaction; 8 CO 2 + 10 H 2 O 2 moles C 4 H 10 react with 13 moles O 2 to produce 8 moles CO 2 and 10 moles H 2 O Use these just like other conversion factors! Problem How many moles of O 2 are required to react with 0. 500 moles of C 4 H 10 according to the balanced equation? 0. 500 mol C 4 H 10 x 13 mol O 2 2 mol C 4 H 10 = 3. 25 mol O 2

Example Problem What mass of CO 2 could be produced from the combustion of 100 g (3 sig fig) of butane (C 4 H 10)? Always convert given quantities (e. g. grams) to moles!!! grams A moles B grams B will need formula masses to convert between grams and moles: CO 2 = 44. 01 g/mol Step 1: “grams A 100 g C 4 H 10 x Step 2: “moles A C 4 H 10 = 58. 12 g/mol moles A” 1 mol C 4 H 10 58. 12 g C 4 H 10 = 1. 721 mol C 4 H 10 moles B” 1. 721 mol C 4 H 10 x 8 mol CO 2 2 mol C 4 H 10 = 6. 884 mol CO 2 continued on next slide…

Example Problem, cont. Step 3: “moles B grams B” 6. 884 mol CO 2 x 44. 01 g CO 2 1 mol CO 2 = 3. 03 x 102 g CO 2 Alternatively, the 3 steps can be combined into one unit analysis equation: 100 g C 4 H 10 x = 1 mol C 4 H 10 58. 12 g C 4 H 10 x 8 mol CO 2 x 44. 01 g CO 2 2 mol C 4 H 10 1 mol CO 2 3. 03 x 102 g CO 2

Limiting Reactant Calculations • In practice, reagents are often combined in a ratio that is different from that in the balanced chemical equation. One of the reactants will be completely consumed and some of the other will remain unreacted. • The limiting reactant is the one that is completely consumed. It determines the maximum amount (yield) of the products. • Whenever quantities of both reactants are given, the limiting reactant must be determined!!!

Example Problem In a commercial process, nitric oxide (NO) is produced: 4 NH 3 + 5 O 2 4 NO + 6 H 2 O What mass (in grams) of NO can be made from the reaction of 30. 00 g NH 3 and 40. 00 g O 2? 1 st, find moles of reactants: 1 mol NH 3 30. 00 g NH 3 x 17. 03 g NH 3 40. 00 g O 2 x 1 mol O 2 32. 00 g O 2 = 1. 762 mol NH 3 = 1. 250 mol O 2 2 nd, calculate amount of product based on each reactant, separately: Yield of NO based on NH 3: 1. 762 mol NH 3 x 4 mol NO 4 mol NH 3 = 1. 762 mol NO continued on next slide…

Example Problem, cont. Yield of NO based on O 2: 1. 250 mol O 2 x 4 mol NO 5 mol O 2 = 1. 000 mol NO Therefore, O 2 is the limiting reactant! (excess of NH 3 exists) A maximum of 1. 000 moles of NO can be produced. 3 rd, calculate yield of product based on limiting reactant: 1. 000 mol NO x 30. 01 g NO 1 mol NO = 30. 01 g NO

Theoretical and Percentage Yield • In actual experiments, the amount of a product that is actually obtained is always somewhat less than that predicted by the stoichiometry of the balanced chemical equations. • This is due to competing reactions and/or mechanical losses in isolation of the product. actual yield -- amount of product obtained experimentally theoretical yield -- amount of product predicted by balanced equation percentage yield -- (actual yield/theoretical yield) x 100%

Example Problem In the previous experiment for the production of NO from 30. 00 g NH 3 and 40. 00 g O 2, the chemist obtained 25. 50 g NO. What is the percentage yield of this reaction? 4 NH 3 + 5 O 2 4 NO + 6 H 2 O Theoretical yield = 30. 01 g NO (based on limiting reactant) Actual yield = 25. 50 g (given in problem) % yield = (25. 50 g NO/30. 01 g NO) x 100% = 85. 0% (Note: the % yield can never be more than 100%!)

Sample Problem The simplest borane known as “diborane-6, ” B 2 H 6, can be prepared from boron trichloride and lithium hydride according to the following balanced equation. 2 BCl 3 + 6 Li. H B 2 H 6 + 6 Li. Cl In one experiment, 20. 0 g of BCl 3 was allowed to react with 5. 00 g of Li. H. After isolation and purification of the reaction product, 2. 05 g of pure B 2 H 6 was actually obtained. Calculate the percentage yield of this reaction. Formula masses (g/mol): BCl 3 = 117. 2 Li. H = 7. 95 B 2 H 6 = 27. 7 Li. Cl = 42. 4

Sample Problem The simplest borane known as “diborane-6, ” B 2 H 6, can be prepared from boron trichloride and lithium hydride according to the following balanced equation. 2 BCl 3 + 6 Li. H B 2 H 6 + 6 Li. Cl In one experiment, 20. 0 g of BCl 3 was allowed to react with 5. 00 g of Li. H. After isolation and purification of the reaction product, 2. 05 g of pure B 2 H 6 was actually obtained. Calculate the percentage yield of this reaction. Formula masses (g/mol): BCl 3 = 117. 2 Li. H = 7. 95 B 2 H 6 = 27. 7 Li. Cl = 42. 4 Answer: 86. 9%

Reactions in Aqueous Solution Terminology solution -- homogeneous (uniform) mixture consisting of: solvent - the bulk medium, e. g. H 2 O, solute(s) - the dissolved substance(s), e. g. Na. Cl concentration -- measure of relative solute/solvent ratio --concentrated vs. dilute standard solution -- accurately known concentration saturated solution -- contains maximum amount of solute solubility -- concentration of a saturated solution, e. g. : solubility of Na. Cl is about 36 g Na. Cl/100 g H 2 O (“soluble”) solubility of Cu. S is about 10 -5 g Cu. S/100 g H 2 O (“insoluble”) precipitate -- an “insoluble” reaction product e. g. a precipitation reaction where the precipitate is Ag. Cl: Na. Cl(aq) + Ag. NO 3(aq) --> Ag. Cl(s) + Na. NO 3(aq)

Solution Concentration • Molar Concentration Molarity (M) = moles solute/liter of solution Units: moles/L or moles/1000 m. L (just a conversion factor!) e. g. a “ 0. 10 M” Na. Cl solution contains 0. 10 mole Na. Cl per liter of solution Problem What mass of Na. Cl is required to prepare 300 m. L of 0. 100 M solution? 1 st--find moles of Na. Cl required: 300 m. L x 0. 100 mol Na. Cl 1000 m. L solution = 0. 0300 mol Na. Cl 2 nd--convert to grams of Na. Cl: 0. 0300 mol Na. Cl x 58. 44 g Na. Cl 1 mole Na. Cl = 1. 75 g Na. Cl Prepare this solution by weighing 1. 75 g Na. Cl, dissolving in some H 2 O (about 250 m. L), and then diluting to the 300 m. L mark.

Sample Problems Calculate the molarity of a solution made by dissolving 23. 4 g of sodium sulfate in enough water to form 125 m. L of solution. The label of a stock bottle of aqueous ammonia indicates that the solution is 28% ammonia by mass and has a density of 0. 898 g/m. L. Calculate the molarity of the solution.

Sample Problems Calculate the molarity of a solution made by dissolving 23. 4 g of sodium sulfate in enough water to form 125 m. L of solution. Answer: 1. 32 M Na 2 SO 4 The label of a stock bottle of aqueous ammonia indicates that the solution is 28% ammonia by mass and has a density of 0. 898 g/m. L. Calculate the molarity of the solution. Answer: 15 M NH 3

Dilution of Concentrated Solutions Concentrated solution + H 2 O --> dilute solution (moles solute)conc = (moles solute)dil V c Mc = V d Md Problem A 5. 00 M Na. Cl “stock” solution is available. How would you prepare 300 m. L of a 0. 100 M Na. Cl “standard” solution? Vc x (5. 00 M) = (300 m. L) x (0. 100 M) Vc = (300 m. L) x (0. 100 M)/(5. 00 M) = 6. 00 m. L Measure out 6. 00 m. L of the 5. 00 M “stock” solution, then H 2 O to a total volume of 300 m. L. add

Stoichiometry Problems -- Reactions in Solution Start with a Balanced Equation and Use the Mole Method (Molarity is just a conversion factor!) Problem For the following reaction, 2 Ag. NO 3(aq) + Ca. Cl 2(aq) --> 2 Ag. Cl(s) + Ca(NO 3)2(aq) a) What volume of 0. 250 M Ag. NO 3 is required to react completely with 250 m. L of 0. 400 M Ca. Cl 2? b) What mass of Ag. Cl should be produced? Part (a): volume of Ag. NO 3? 1 st, find moles of Ca. Cl 2 (250 m. L Ca. Cl 2 soln) x 0. 400 mol Ca. Cl 2 1000 m. L Ca. Cl 2 soln = 0. 100 mol Ca. Cl 2 2 nd, find moles of Ag. NO 3 (0. 100 mol Ca. Cl 2) x 2 mol Ag. NO 3 1 mol Ca. Cl 2 = 0. 200 mol Ag. NO 3

Example Problem, cont. 3 rd, find volume of Ag. NO 3 solution (0. 200 mole Ag. NO 3) x 1000 m. L Ag. NO 3 soln 0. 250 mol Ag. NO 3 = 800 m. L Ag. NO 3 solution Part (b): mass of Ag. Cl? 2 mol Ag. Cl 0. 100 mol Ca. Cl 2 x (0. 200 mol Ag. Cl) x 1 mol Ca. Cl 2 143 g Ag. Cl 1 mol Ag. Cl = 0. 200 mol Ag. Cl = 28. 6 g Ag. Cl WORK MORE PROBLEMS!!

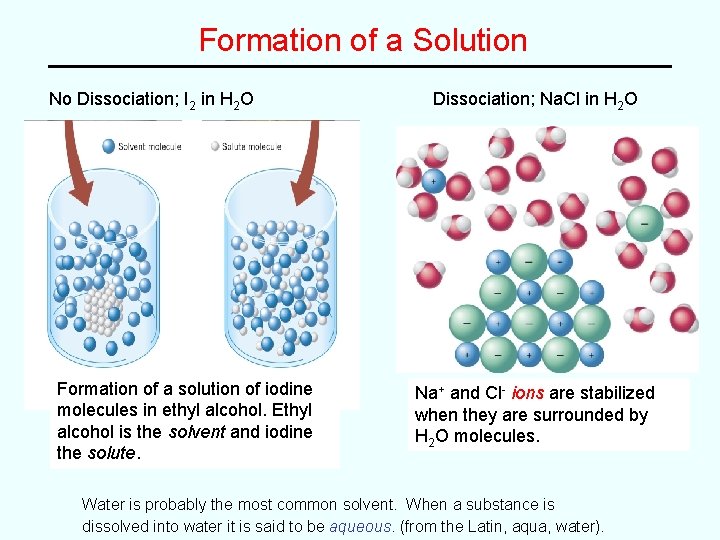
Formation of a Solution No Dissociation; I 2 in H 2 O Formation of a solution of iodine molecules in ethyl alcohol. Ethyl alcohol is the solvent and iodine the solute. Dissociation; Na. Cl in H 2 O Na+ and Cl- ions are stabilized when they are surrounded by H 2 O molecules. Water is probably the most common solvent. When a substance is dissolved into water it is said to be aqueous. (from the Latin, aqua, water).

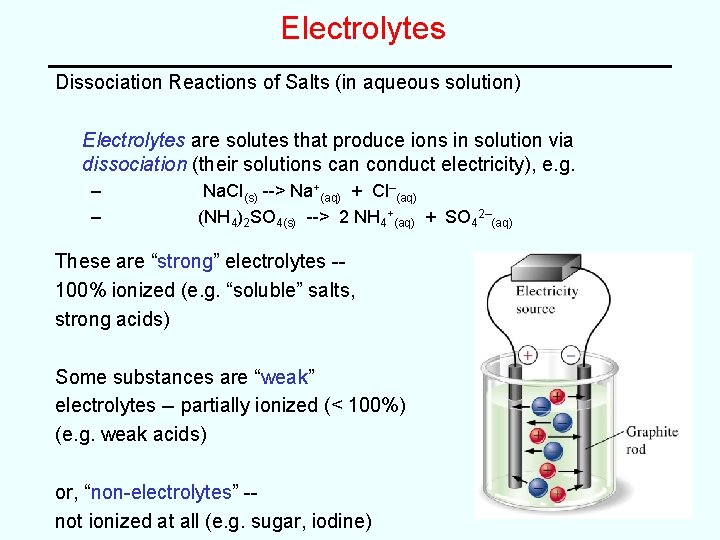
Electrolytes Dissociation Reactions of Salts (in aqueous solution) Electrolytes are solutes that produce ions in solution via dissociation (their solutions can conduct electricity), e. g. – – Na. Cl(s) --> Na+(aq) + Cl–(aq) (NH 4)2 SO 4(s) --> 2 NH 4+(aq) + SO 42–(aq) These are “strong” electrolytes -100% ionized (e. g. “soluble” salts, strong acids) Some substances are “weak” electrolytes -- partially ionized (< 100%) (e. g. weak acids) or, “non-electrolytes” -not ionized at all (e. g. sugar, iodine)

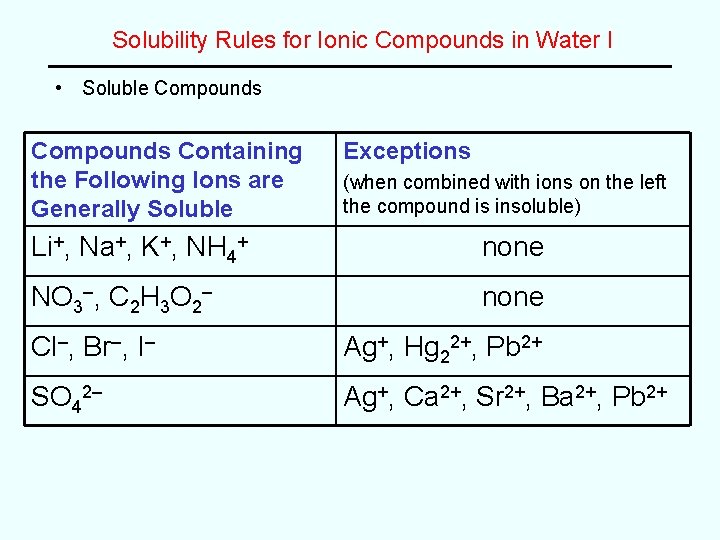
Solubility Rules for Ionic Compounds in Water I • Soluble Compounds Containing the Following Ions are Generally Soluble Exceptions (when combined with ions on the left the compound is insoluble) Li+, Na+, K+, NH 4+ none NO 3–, C 2 H 3 O 2– none Cl–, Br–, I– Ag+, Hg 22+, Pb 2+ SO 42– Ag+, Ca 2+, Sr 2+, Ba 2+, Pb 2+

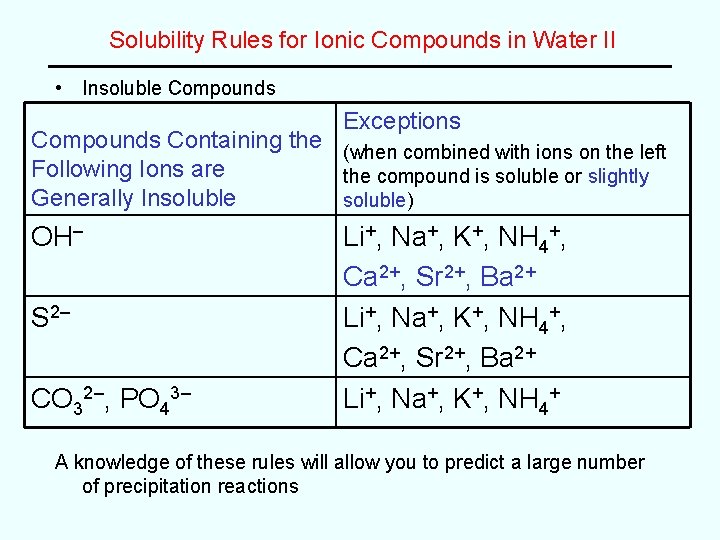
Solubility Rules for Ionic Compounds in Water II • Insoluble Compounds Exceptions Compounds Containing the (when combined with ions on the left Following Ions are the compound is soluble or slightly Generally Insoluble) OH– S 2– CO 32–, PO 43– Li+, Na+, K+, NH 4+, Ca 2+, Sr 2+, Ba 2+ Li+, Na+, K+, NH 4+ A knowledge of these rules will allow you to predict a large number of precipitation reactions

Sample Questions Write the equations for the dissociation of the following ionic compounds. a) KBr b) Na 2 SO 4 c) Zn. Cl 2

Sample Questions Write the equations for the dissociation of the following ionic compounds. a) KBr(s) --> K+(aq) + Br–(aq) b) Na 2 SO 4(s) --> 2 Na+(aq) + SO 42–(aq) c) Zn. Cl 2(s) --> Zn 2+(aq) + 2 Cl–(aq)

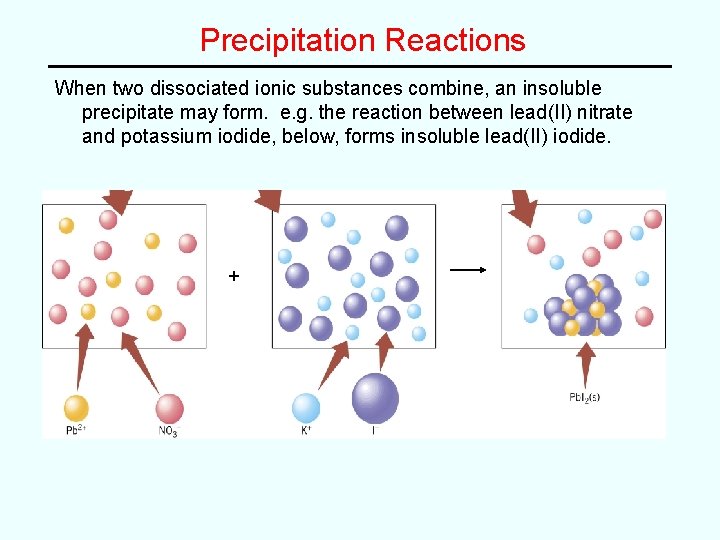
Precipitation Reactions When two dissociated ionic substances combine, an insoluble precipitate may form. e. g. the reaction between lead(II) nitrate and potassium iodide, below, forms insoluble lead(II) iodide. +

Ionic Reactions in Aqueous Solution • Equations for Ionic Reactions Metathesis Reaction (also called “double displacement”) Ions from two different reactants simply trade partners, e. g. : Na 2 CO 3(aq) + Ba(NO 3)2(aq) --> Ba. CO 3(s) + 2 Na. NO 3(aq) This was written as a molecular equation in which all reactants and products are shown as complete, neutral chemical formulas. It could also have been written as a complete ionic equation in which all soluble ionic compounds are split up into their ions, e. g. ; 2 Na+(aq) + CO 32–(aq) + Ba 2+(aq) + 2 NO 3–(aq) --> Ba. CO 3(s) + 2 Na+(aq) + 2 NO 3–(aq)

Equations for Ionic Rxns, cont. 2 Na+(aq) + CO 32–(aq) + Ba 2+(aq) + 2 NO 3–(aq) --> Ba. CO 3(s) + 2 Na+(aq) + 2 NO 3–(aq) Here, the Na+ and NO 3– ions are called “spectator ions” because they appear unchanged on both sides of the equation. The spectator ions do not participate in the chemically important part of the reaction -- the precipitation of Ba. CO 3. The essential chemical process can be written without the spectator ions in the net ionic equation, e. g. : Ba 2+(aq) + CO 32–(aq) --> Ba. CO 3(s) The net ionic equation shows that, in general, a precipitate of Ba. CO 3 will form whenever the ions Ba 2+ and CO 32– are combined in aqueous solution, regardless of their sources. Both atoms and charge must balance!

Strategy 1. 2. Dissociate the ionic compounds into their ions. Look at the reaction and see what the combinations of ions could be. 3. Consult your memory or solubility charts to determine the solubility of the product. 4. Balance the equation(s). Example Problem Will a precipitate form when aqueous solutions of Ca. Cl 2 and K 3 PO 4 are mixed? Write balanced molecular, ionic, and net ionic equations for the reaction. Step 1: Write the possible ions: Ca 2+, Cl–, K+, PO 43– Step 2: Look at the combinations; KCl, Ca 3(PO 4)2 Step 3: You know KCl is soluble, Ca 3(PO 4)2 is not, so a precipitate will form. Step 4: Balance the equation: 3 Ca. Cl 2 + 2 K 3 PO 4 --> Ca 3(PO 4)2 + 6 KCl

Example Problem, cont. Molecular equation is: 3 Ca. Cl 2(aq) + 2 K 3 PO 4(aq) --> Ca 3(PO 4)2(s) + 6 KCl(aq) The ionic equation: 3 Ca 2+(aq) + 6 Cl–(aq) + 6 K+(aq) + 2 PO 43–(aq) --> Ca 3(PO 4)2(s) + 6 K+(aq) + 6 Cl–(aq) Ions that do not participate in the reaction are called spectator ions. Net ionic equation is: 3 Ca 2+(aq) + 2 PO 43–(aq) --> Ca 3(PO 4)2(s)

Summary of 3 Types of Balanced Chemical Equations • Molecular Equation – Shows all compounds with complete, neutral molecular formulas – Useful in planning experiments and stoichiometry calculations • Ionic Equation (complete) – All strong electrolytes are shown in their dissociated, ionic forms – Insoluble substances and weak electrolytes are shown in their molecular form – “spectator ions” are included – Useful for showing all details of what is happening in the reaction

Summary of 3 Types of Balanced Chemical Equations, cont. • Net Ionic Equation – “spectator ions” are omitted – Only the essential chemical process is shown, i. e. formation of a : • Solid precipitate • Gaseous product, or • Weak electrolyte (e. g. water) – Useful for generalizing the reaction -- same important product can often be formed from different sets of reactants • When will a precipitate form? – KNOW THE SOLUBILITY RULES -- TABLE 4. 1

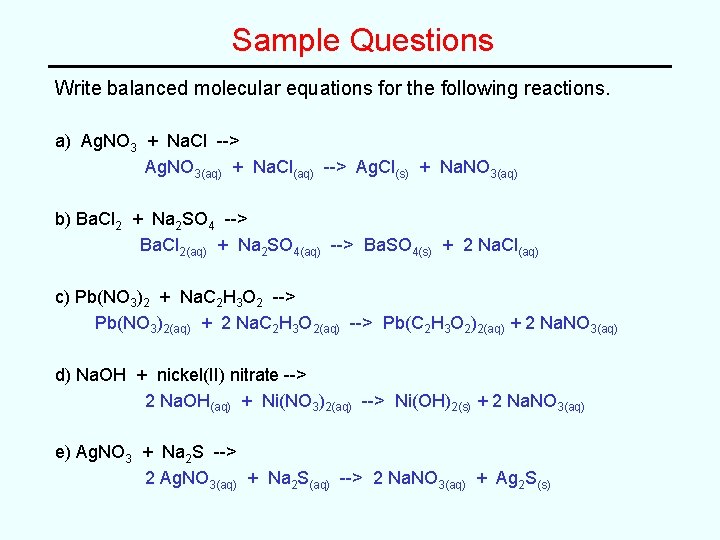
Sample Questions Write balanced molecular equations for the following reactions. a) Ag. NO 3 + Na. Cl --> b) Ba. Cl 2 + Na 2 SO 4 --> c) Pb(NO 3)2 + Na. C 2 H 3 O 2 --> d) Na. OH + nickel(II) nitrate --> e) Ag. NO 3 + Na 2 S -->

Sample Questions Write balanced molecular equations for the following reactions. a) Ag. NO 3 + Na. Cl --> Ag. NO 3(aq) + Na. Cl(aq) --> Ag. Cl(s) + Na. NO 3(aq) b) Ba. Cl 2 + Na 2 SO 4 --> Ba. Cl 2(aq) + Na 2 SO 4(aq) --> Ba. SO 4(s) + 2 Na. Cl(aq) c) Pb(NO 3)2 + Na. C 2 H 3 O 2 --> Pb(NO 3)2(aq) + 2 Na. C 2 H 3 O 2(aq) --> Pb(C 2 H 3 O 2)2(aq) + 2 Na. NO 3(aq) d) Na. OH + nickel(II) nitrate --> 2 Na. OH(aq) + Ni(NO 3)2(aq) --> Ni(OH)2(s) + 2 Na. NO 3(aq) e) Ag. NO 3 + Na 2 S --> 2 Ag. NO 3(aq) + Na 2 S(aq) --> 2 Na. NO 3(aq) + Ag 2 S(s)

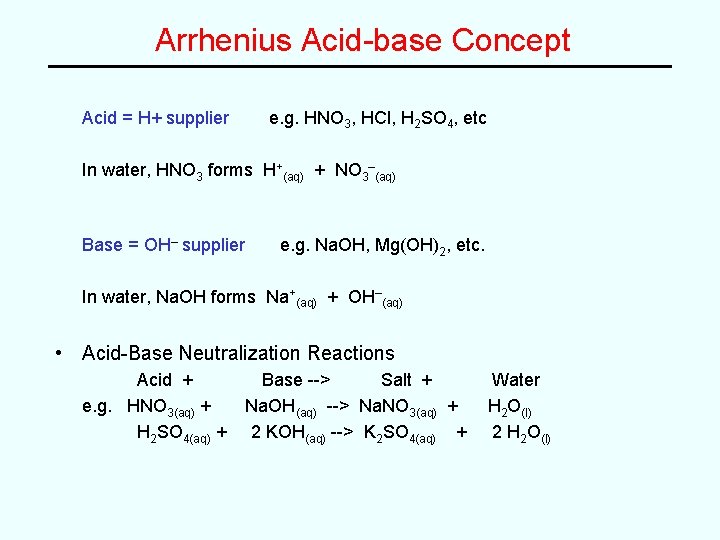
Arrhenius Acid-base Concept Acid = H+ supplier e. g. HNO 3, HCl, H 2 SO 4, etc In water, HNO 3 forms H+(aq) + NO 3–(aq) Base = OH– supplier e. g. Na. OH, Mg(OH)2, etc. In water, Na. OH forms Na+(aq) + OH–(aq) • Acid-Base Neutralization Reactions Acid + e. g. HNO 3(aq) + H 2 SO 4(aq) + Base --> Salt + Na. OH(aq) --> Na. NO 3(aq) + 2 KOH(aq) --> K 2 SO 4(aq) + Water H 2 O(l) 2 H 2 O(l)

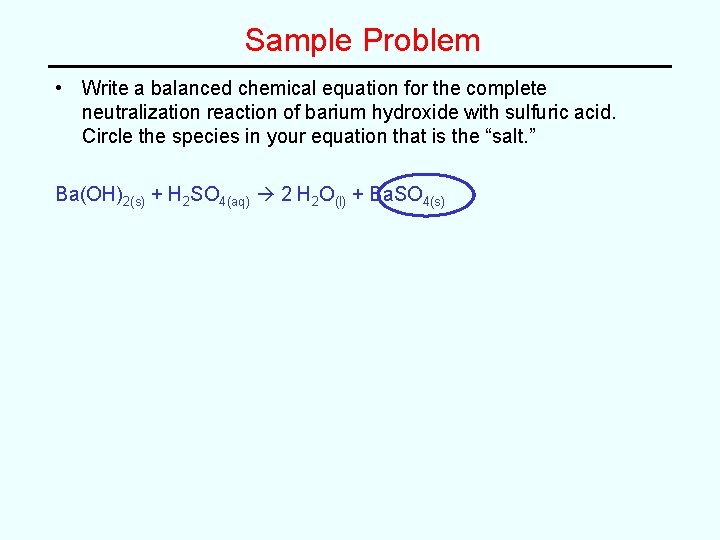
Sample Problem • Write a balanced chemical equation for the complete neutralization reaction of barium hydroxide with sulfuric acid. Circle the species in your equation that is the “salt. ”

Sample Problem • Write a balanced chemical equation for the complete neutralization reaction of barium hydroxide with sulfuric acid. Circle the species in your equation that is the “salt. ” Ba(OH)2(s) + H 2 SO 4(aq) 2 H 2 O(l) + Ba. SO 4(s)

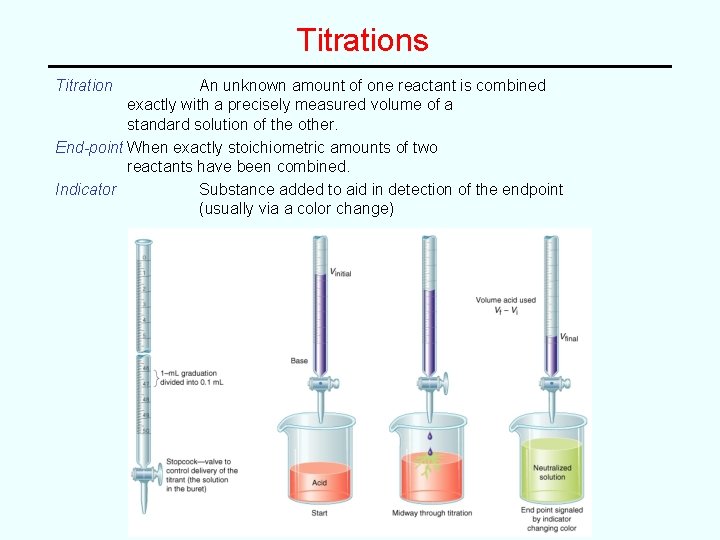
Titrations Titration An unknown amount of one reactant is combined exactly with a precisely measured volume of a standard solution of the other. End-point When exactly stoichiometric amounts of two reactants have been combined. Indicator Substance added to aid in detection of the endpoint (usually via a color change)

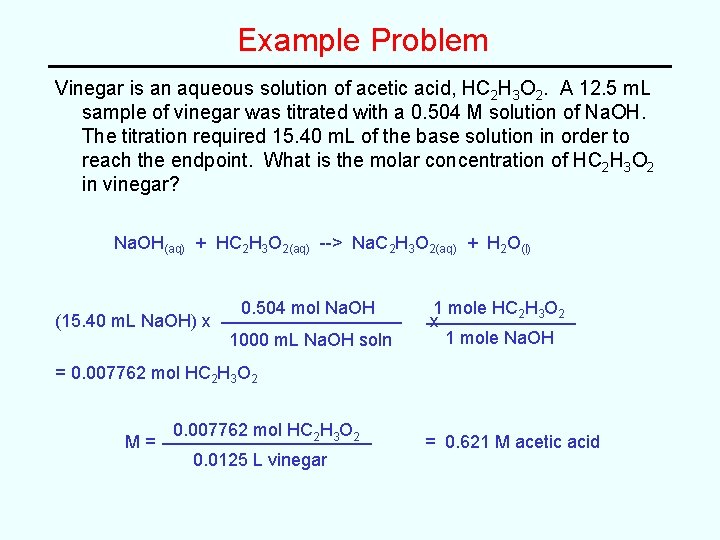
Example Problem Vinegar is an aqueous solution of acetic acid, HC 2 H 3 O 2. A 12. 5 m. L sample of vinegar was titrated with a 0. 504 M solution of Na. OH. The titration required 15. 40 m. L of the base solution in order to reach the endpoint. What is the molar concentration of HC 2 H 3 O 2 in vinegar? Na. OH(aq) + HC 2 H 3 O 2(aq) --> Na. C 2 H 3 O 2(aq) + H 2 O(l) (15. 40 m. L Na. OH) x 0. 504 mol Na. OH 1000 m. L Na. OH soln 1 mole HC 2 H 3 O 2 x 1 mole Na. OH = 0. 007762 mol HC 2 H 3 O 2 M= 0. 007762 mol HC 2 H 3 O 2 0. 0125 L vinegar = 0. 621 M acetic acid

Sample Problem A new fluorocarbon material recently prepared at TCU is believed to be a diprotic acid (call it H 2 A for short). A 0. 860 g sample of this unknown acid was titrated (reaction below) with a 0. 1025 M solution of Na. OH. In the titration, 38. 50 m. L of the Na. OH solution was required to reach the endpoint. Calcuate the molecular mass of the new acid. H 2 A + 2 Na. OH --> Na 2 A + 2 H 2 O

Sample Problem A new fluorocarbon material recently prepared at TCU is believed to be a diprotic acid (call it H 2 A for short). A 0. 860 g sample of this unknown acid was titrated (reaction below) with a 0. 1025 M solution of Na. OH. In the titration, 38. 50 m. L of the Na. OH solution was required to reach the endpoint. Calcuate the molecular mass of the new acid. H 2 A + 2 Na. OH --> Na 2 A + 2 H 2 O Answer: 436 g/mol

Gas Evolution Reactions Reactant Type Reacts with Ion Exchange Product Decom Gas -pose? Formed Example Mn. S, MHS acid H 2 S no H 2 S K 2 S(aq) + 2 HCl(aq) 2 KCl(aq) + H 2 S(g) Mn. CO 3, MHCO 3 acid H 2 CO 3 yes CO 2 K 2 CO 3(aq) + 2 HCl(aq) 2 KCl(aq) + CO 2(g) + H 2 O(l) Mn. SO 3 MHSO 3 acid H 2 SO 3 yes SO 2 K 2 SO 3(aq) + 2 HCl(aq) 2 KCl(aq) + SO 2(g) + H 2 O(l) (NH 4)nanion base NH 4 OH yes NH 3 KOH(aq) + NH 4 Cl(aq) KCl(aq) + NH 3(g) + H 2 O(l)

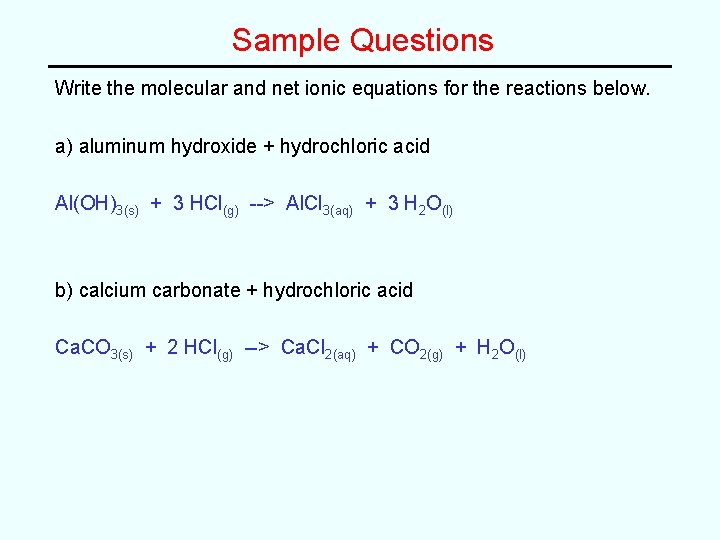
Sample Questions Write the molecular and net ionic equations for the reactions below. a) aluminum hydroxide + hydrochloric acid b) calcium carbonate + hydrochloric acid

Sample Questions Write the molecular and net ionic equations for the reactions below. a) aluminum hydroxide + hydrochloric acid Al(OH)3(s) + 3 HCl(g) --> Al. Cl 3(aq) + 3 H 2 O(l) b) calcium carbonate + hydrochloric acid Ca. CO 3(s) + 2 HCl(g) --> Ca. Cl 2(aq) + CO 2(g) + H 2 O(l)

Oxidation - Reduction Reactions Redox Terminology redox reaction -- electron transfer process e. g. , 2 Na + Cl 2 --> 2 Na. Cl Related terms: oxidizing agent = the substance that gets reduced (Cl 2) reducing agent = the substance that gets oxidized (Na) Oxidation and reduction always occur together so that there is no net loss or gain of electrons overall.

OILRIG • • • O I L R I G Oxidation Is Loss Reduction Is Gain

Oxidation Numbers (Oxidation States) Oxidation number a “charge” that is assigned to an atom to aid in balancing redox reactions The oxidation state is the atomic number (no. of positive charges) minus the number of electrons that it is said to have. Oxidation: the oxidation state increases. Reduction: the oxidation state decreases. Rules for assigning oxidation numbers -- see page 164 Learn the rules by working examples!

Assigning Oxidation States 1. 2. 3. 4. 5. 6. Oxidation state of a free element is zero. Oxidation state of a simple monoatomic ion is equal to the charge on the ion. Sum of all the oxidation numbers must equal the charge on the particle. In its compounds, H and Group 1 A metals have an oxidation number of +1. Group 2 A metals have an oxidation number of +2. In its compounds, fluorine has an oxidation state of -1. In its compounds, oxygen has an oxidation state of -2. If there is a conflict between two rules, apply the rule with the lower number and ignore the conflicting rule. e. g. assign all oxidation numbers in: Ag 2 S Cl. O 3– Cl. O 4– Cr(NO 3)3 H 2 O H 2 O 2

Assigning Oxidation States 1. 2. Oxidation state of a free element is zero. Oxidation state of a simple monoatomic ion is equal to the charge on the ion. Sum of all the oxidation numbers must equal the charge on the particle. In its compounds, H and Group 1 A metals have an oxidation number of +1. Group 2 A metals have an oxidation number of +2. In its compounds, fluorine has an oxidation state of -1. In its compounds, oxygen has an oxidation state of -2. 3. 4. 5. 6. If there is a conflict between two rules, apply the rule with the lower number and ignore the conflicting rule. e. g. assign all oxidation numbers in: +1 -2 +5 -2 Ag 2 S Cl. O 3– +7 -2 Cl. O 4– +3 +5 -2 Cr(NO 3)3 +1 -2 +1 -1 H 2 O H 2 O 2

Sample Problems --Note that fractional values of oxidation numbers are allowed. More examples: NH 3 PCl 5 Fe. S Na 2 O Mg 2 Ti. O 4 V(C 2 H 3 O 2)3 HPO 42– K 2 Cr 2 O 7

Sample Problems --Note that fractional values of oxidation numbers are allowed. More examples: NH 3 N -3, H +1 PCl 5 P +5, Cl -1 Fe. S Fe +2, S -2 Na 2 O Na +1, O -2 Mg 2 Ti. O 4 Mg +2, Ti +4, O -2 V(C 2 H 3 O 2)3 V +3, C 0, H +1, O -2 HPO 42– H +1, P +5, O -2 K 2 Cr 2 O 7 K +1, Cr +6, O -2

Redox Reactions • The transfer of electrons between species, meaning that one species is oxidized and one is reduced. The two processes will always occur together. • When has a redox reaction occurred? – If there is a change in the oxidation state of any element in the reaction, a redox reaction has happened. – Remember that if something is oxidized, something else must be reduced! (and vice-versa) More examples: 2 Ca(s) + O 2(g) --> 2 Ca. O(s) 2 Al(s) + 3 Cl 2(g) --> 2 Al. Cl 3(s)

Example Problems • When H 2 O 2 (hydrogen peroxide) is used as an antiseptic it oxidizes bacteria. What product might it form, O 2 or H 2 O? • Answer: In the starting material O is in the -1 oxidation state. If it oxidizes bacteria, it must get reduced, which means its oxidation number goes down. O 2 has an oxidation number of 0, while the O in H 2 O has an oxidation number of -2. Therefore H 2 O is the product of reduction of hydrogen peroxide. In the following reactions, state which compounds are oxidized and which are reduced. • 2 Al(s) + 3 I 2(s) --> 2 Al. I 3(s) • 2 Pb. S(s) + 3 O 2(g) --> 2 Pb. O(s) + 2 SO 2(g) • 2 KCl(aq) + Mn. O 2(s) + 2 H 2 SO 4(aq) --> K 2 SO 4(aq) + Mn. SO 4(aq) + Cl 2(g) + 2 H 2 O(l) • Answer: Oxidized: Al, S, Cl, and Reduced: I, O, Mn.

Sample Problem In the following redox reaction, 14 HNO 3(aq) + 4 K 2 C 2 O 4(aq) + K 2 Cr 2 O 7(aq) --> 8 CO 2(g) + 2 Cr(NO 3)2(aq) + 10 KNO 3(aq) + 7 H 2 O(l) A) what is the substance oxidized? B) what is the oxidizing agent? C) what are the oxidation numbers of each atom in Cr(NO 3)2?

Sample Problem In the following redox reaction, 14 HNO 3(aq) + 4 K 2 C 2 O 4(aq) + K 2 Cr 2 O 7(aq) --> 8 CO 2(g) + 2 Cr(NO 3)2(aq) + 10 KNO 3(aq) + 7 H 2 O(l) A) what is the substance oxidized? B) what is the oxidizing agent? C) what are the oxidation numbers of each atom in Cr(NO 3)2? Answer: a) K 2 C 2 O 4 is oxidized b) The oxidizing agent is K 2 Cr 2 O 7 c) Cr is +2, N is +5, O is -2

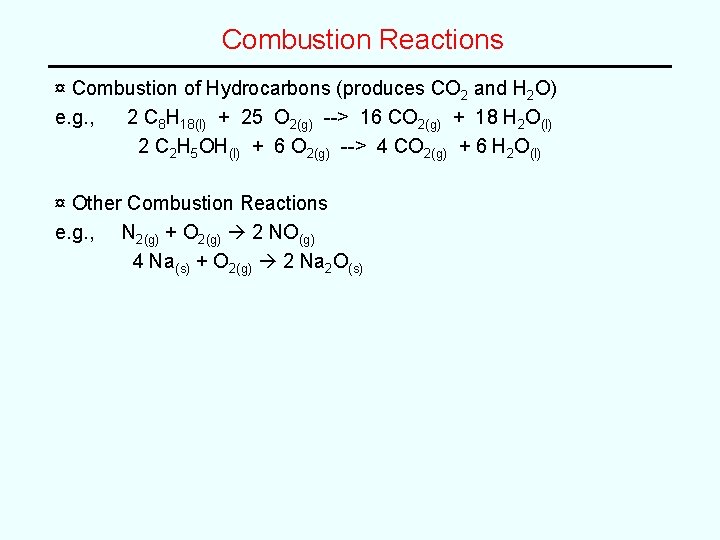
Combustion Reactions ¤ Combustion of Hydrocarbons (produces CO 2 and H 2 O) e. g. , 2 C 8 H 18(l) + 25 O 2(g) --> 16 CO 2(g) + 18 H 2 O(l) 2 C 2 H 5 OH(l) + 6 O 2(g) --> 4 CO 2(g) + 6 H 2 O(l) ¤ Other Combustion Reactions e. g. , N 2(g) + O 2(g) 2 NO(g) 4 Na(s) + O 2(g) 2 Na 2 O(s)