Ch 4 Boolean Algebra and Logic Simplification Boolean

Ch. 4 Boolean Algebra and Logic Simplification ü ü ü ü Boolean Operations and Expressions Laws and Rules of Boolean Algebra Boolean Analysis of Logic Circuits Simplification Using Boolean Algebra Standard Forms of Boolean Expressions Truth Table and Karnaugh Map Programmable Logic: PALs and GALs Boolean Expressions with VHDL 1

Introduction 2 Boolean Algebra • George Boole(English mathematician), 1854 • Boolean Algebra {(1, 0), Var, (NOT, AND, OR), Thms} Mathematical tool to expression and analyze digital (logic) circuits Claude Shannon, the first to apply Boole’s work, 1938 • “An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities” – • “A Symbolic Analysis of Relay and Switching Circuits” at MIT This chapter covers Boolean algebra, Boolean expression and its evaluation and simplification, and VHDL program Bzu. Pages. COM

Basic Functions Boolean functions : NOT, AND, OR, exclusive OR(XOR) : odd function exclusive NOR(XNOR) : even function(equivalence) Bzu. Pages. COM 3

Basic Functions (계속) • AND Z=X Y or Z=XY Z=1 if and only if X=1 and Y=1, otherwise Z=0 • OR Z=X + Y Z=1 if X=1 or if Y=1, or both X=1 and Y=1. Z=0 if and only if X=0 and Y=0 • NOT Z=X or Z=1 if X=0, Z=0 if X=1 Bzu. Pages. COM 4

Basic Functions (계속) Bzu. Pages. COM 5

Boolean Operations and Expressions • Boolean Addition – Logical OR operation Ex 4 -1) Determine the values of A, B, C, and D that make the sum term A+B’+C+D’ Sol) all literals must be ‘ 0’ for the sum term to be ‘ 0’ A+B’+C+D’=0+1’+0+1’=0 A=0, B=1, C=0, and D=1 • Boolean Multiplication – Logical AND operation Ex 4 -2) Determine the values of A, B, C, and D for AB’CD’=1 Sol) all literals must be ‘ 1’ for the product term to be ‘ 1’ AB’CD’=10’ 10’=1 A=1, B=0, C=1, and D=0 Bzu. Pages. COM 6

Basic Identities of Boolean Algebra The relationship between a single variable X, its complement X , and the binary constants 0 and 1 Bzu. Pages. COM 7

Laws of Boolean Algebra • Commutative Law the order of literals does not matter –A + B = B + A –A B=BA Bzu. Pages. COM 8

Laws of Boolean Algebra (계속) • Associative Law the grouping of literals does not matter – A + (B + C) = (A + B) + C (=A+B+C) – A(BC) Bzu. Pages. COM = (AB)C (=ABC) 9

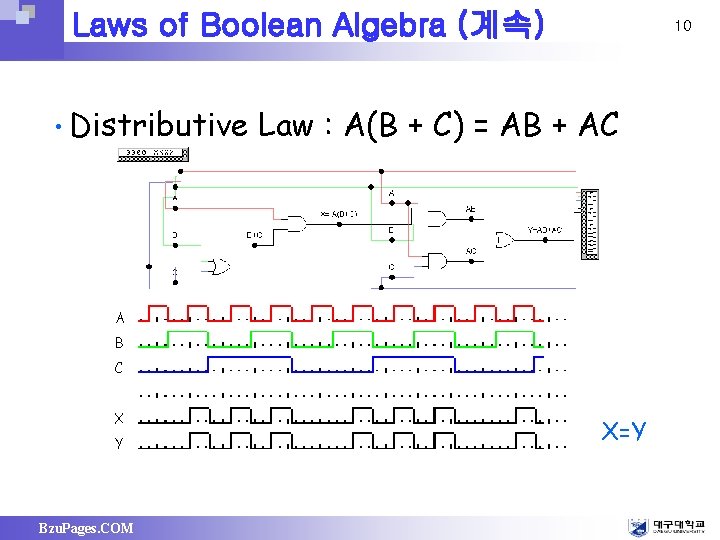
Laws of Boolean Algebra (계속) • Distributive 10 Law : A(B + C) = AB + AC A B C X Y Bzu. Pages. COM X=Y

Laws of Boolean Algebra (계속) 11 (A+B)(C+D) = AC + AD + BC + BD A B C D X Y Bzu. Pages. COM X=Y

Rules of Boolean Algebra 12 A+0=A In math if you add 0 you have changed nothing in Boolean Algebra ORing with 0 changes nothing ü A X Bzu. Pages. COM X=A+0 =A

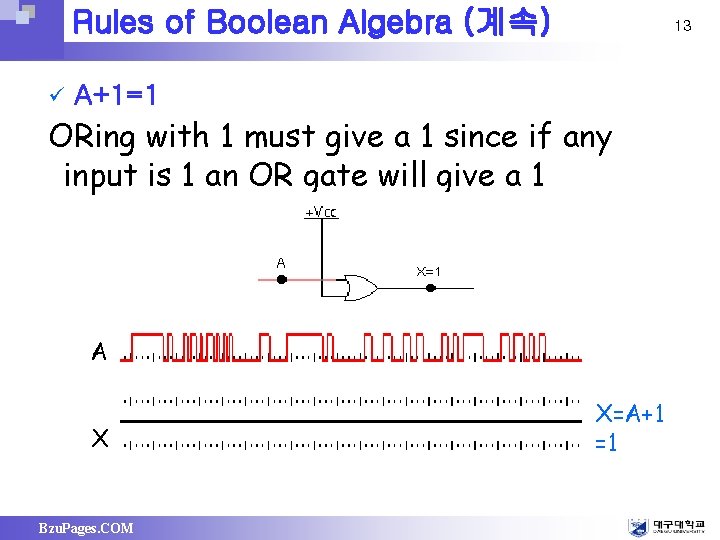
Rules of Boolean Algebra (계속) ü 13 A+1=1 ORing with 1 must give a 1 since if any input is 1 an OR gate will give a 1 A X Bzu. Pages. COM X=A+1 =1

Rules of Boolean Algebra (계속) ü 14 A • 0=0 In math if 0 is multiplied with anything you get 0. If you AND anything with 0 you get 0 A X Bzu. Pages. COM X=A 0 =0

Rules of Boolean Algebra (계속) 15 A • 1 =A ANDing anything with 1 will yield the anything ü A A X Bzu. Pages. COM X=A 1 =A

Rules of Boolean Algebra (계속) ü 16 A+A = A ORing with itself will give the same result A A X Bzu. Pages. COM A=A+A =A

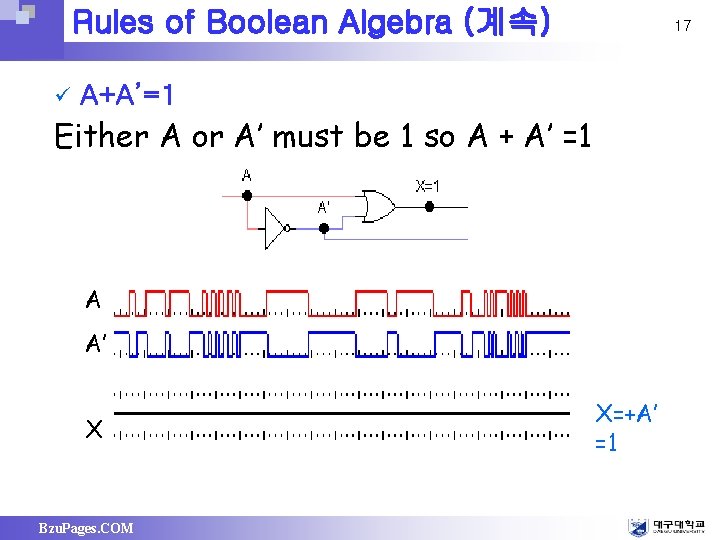
Rules of Boolean Algebra (계속) ü 17 A+A’=1 Either A or A’ must be 1 so A + A’ =1 A A’ X Bzu. Pages. COM X=+A’ =1

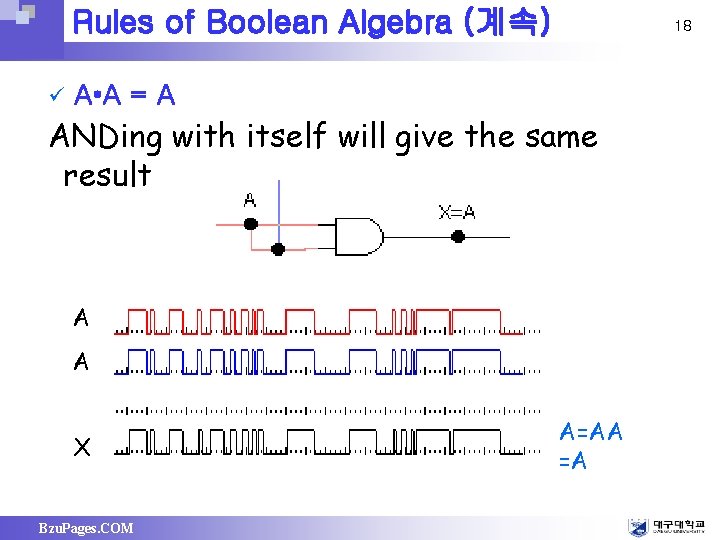
Rules of Boolean Algebra (계속) ü 18 A • A = A ANDing with itself will give the same result A A X Bzu. Pages. COM A=AA =A

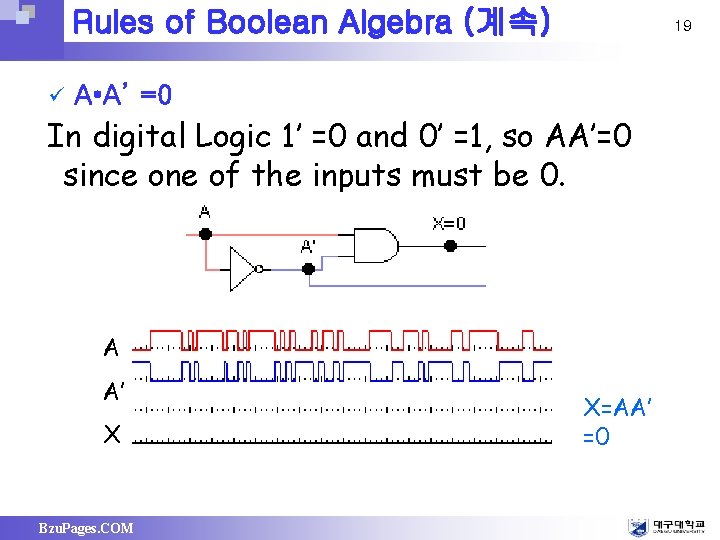
Rules of Boolean Algebra (계속) ü 19 A • A’ =0 In digital Logic 1’ =0 and 0’ =1, so AA’=0 since one of the inputs must be 0. A A’ X Bzu. Pages. COM X=AA’ =0

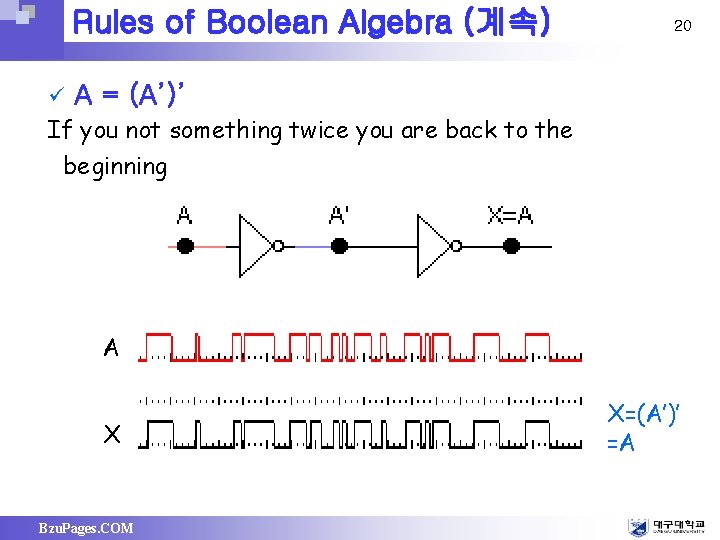
Rules of Boolean Algebra (계속) ü 20 A = (A’)’ If you not something twice you are back to the beginning A X Bzu. Pages. COM X=(A’)’ =A

Rules of Boolean Algebra (계속) ü A + AB = A A B X Bzu. Pages. COM 21

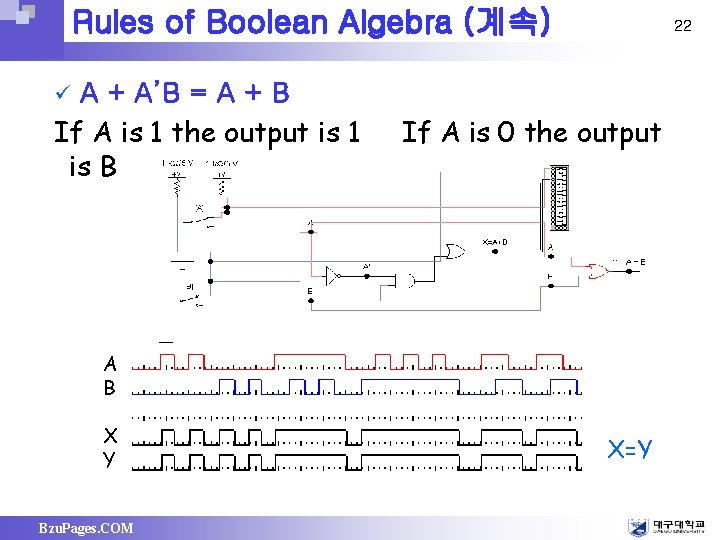
Rules of Boolean Algebra (계속) A + A’B = A + B If A is 1 the output is 1 is B 22 ü If A is 0 the output A B X Y Bzu. Pages. COM X=Y

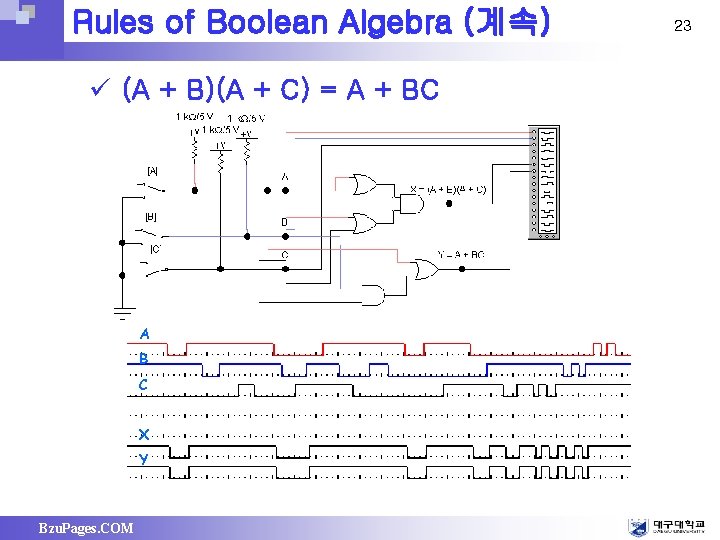
Rules of Boolean Algebra (계속) ü (A + B)(A + C) = A + BC A B C X Y Bzu. Pages. COM 23

De. Morgan’s Theorems • De. Morgan’s Theorem F (A, A , , + , 1, 0) = F(A , A, + , , 0, 1) (A • B)’ = A’ + B’ and (A + B)’ = A’ • B’ – De. Morgan’s theorem will help to simplify digital circuits using NORs and NANDs his theorem states – Bzu. Pages. COM 24

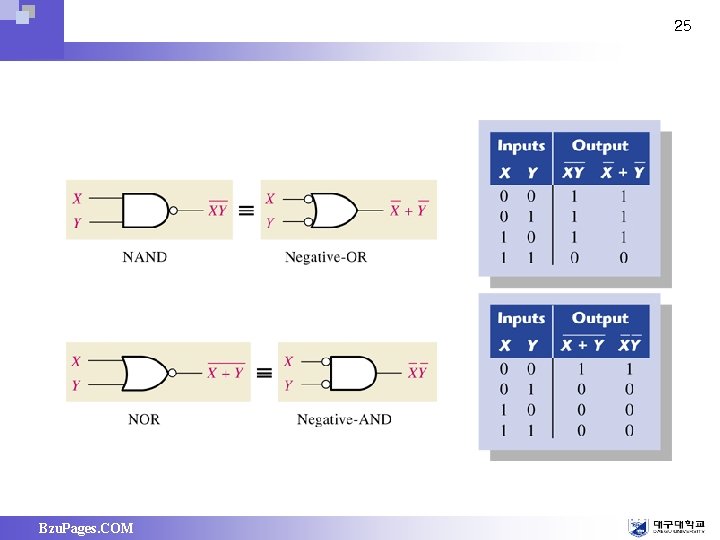
25 Bzu. Pages. COM

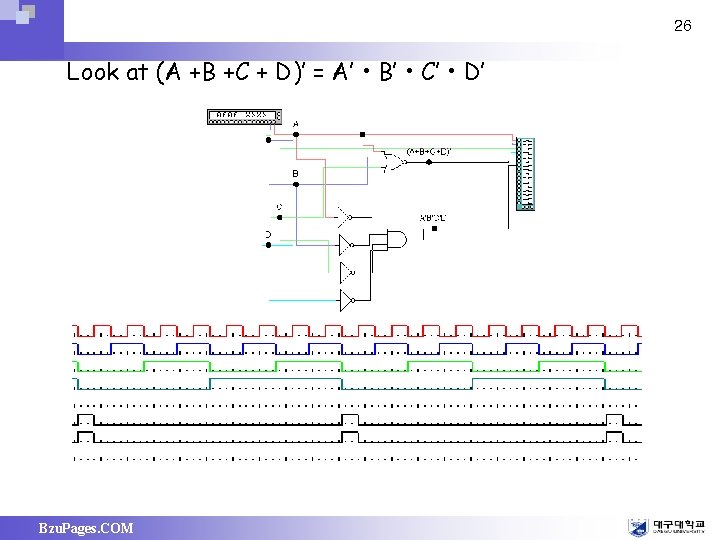
26 Look at (A +B +C + D)’ = A’ • B’ • C’ • D’ Bzu. Pages. COM

27 Ex 4 -3) Apply De. Morgan’s theorems to (XYZ)’ and (X+Y+Z)’ Sol) (XYZ)’=X’+Y’+Z’ and (X+Y+Z)’=X’Y’Z’ Ex 4 -5) Apply De. Morgan’s theorems to (a) ((A+B+C)D)’ (b) (ABC+DEF)’ (c) (AB’+C’D+EF)’ Sol) (a) ((A+B+C)D)’= (A+B+C)’+D’=A’B’C’+D’ (b) (ABC+DEF)’=(ABC)’(DEF)’=(A’+B’+C’)(D’+E’+F’) (c) (AB’+C’D+EF)’=(AB’)’(C’D)’(EF)’=(A’+B)(C+D’)(E’+F’) Bzu. Pages. COM

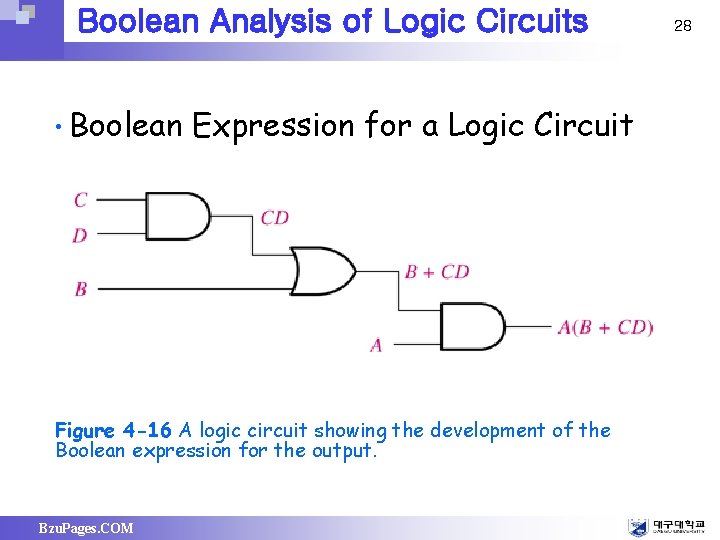
Boolean Analysis of Logic Circuits • Boolean Expression for a Logic Circuit Figure 4 -16 A logic circuit showing the development of the Boolean expression for the output. Bzu. Pages. COM 28

29 • Constructing a Truth Table for a Logic Circuit Convert the expression into the min-terms containing all the input literals – Get the numbers from the min-terms – Putting ‘ 1’s in the rows corresponding to the minterms and ‘ 0’s in the remains – Ex) A(B+CD)=AB(C+C’) (D+D’) +A(B+B’)CD =ABC(D+D’) +ABC’(D+D’) +ABCD+AB’CD =ABCD+ABCD’+ABC’D+ABC’D’ +AB’CD =m 11+m 12+m 13+m 14+m 15= (11, 12, 13, 14, 15) Bzu. Pages. COM

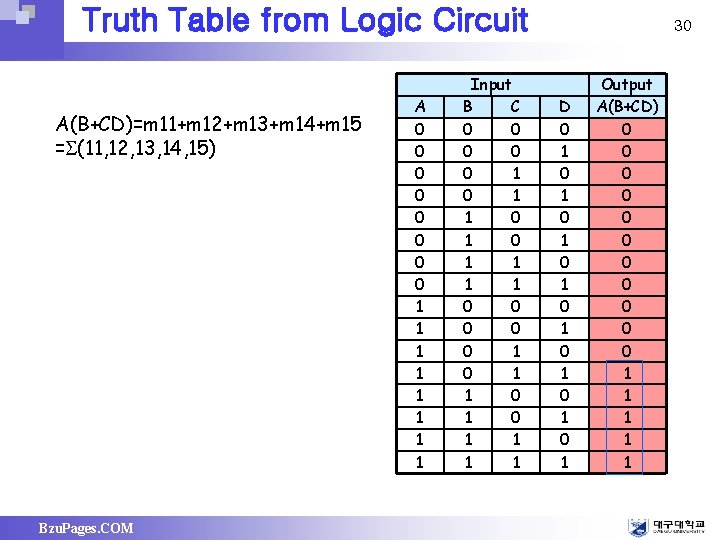
Truth Table from Logic Circuit A(B+CD)=m 11+m 12+m 13+m 14+m 15 = (11, 12, 13, 14, 15) Bzu. Pages. COM A 0 0 0 0 1 1 1 1 Input B C 0 0 0 0 0 1 0 1 1 1 1 30 D 0 1 0 1 Output A(B+CD) 0 0 0 1 1 1

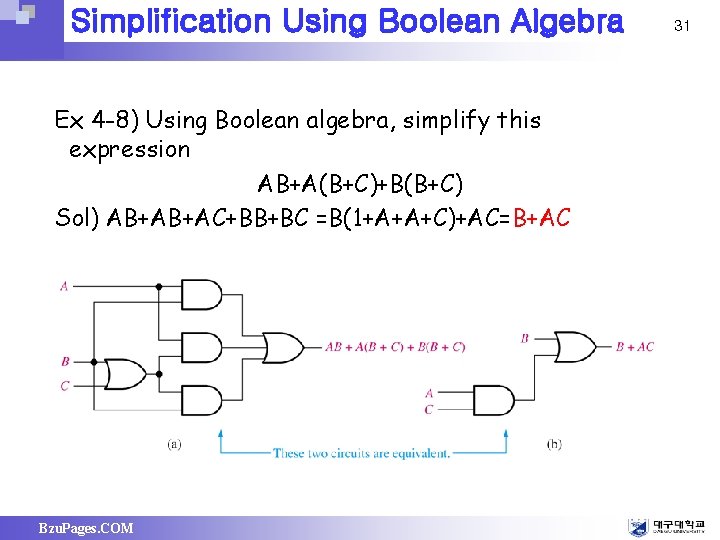
Simplification Using Boolean Algebra Ex 4 -8) Using Boolean algebra, simplify this expression AB+A(B+C)+B(B+C) Sol) AB+AB+AC+BB+BC =B(1+A+A+C)+AC=B+AC Bzu. Pages. COM 31

32 Ex 4 -9) Simplify the following Boolean expression (AB’(C+BD)+A’B’)C Sol) (AB’C+AB’BD+A’B’)C=AB’CC+A’B’C=(A+A’)B’C=B’C Ex 4 -10) Simplify the following Boolean expression A’BC+AB’C’+A’B’C’+AB’C+ABC Sol) (A+A’)BC+(A+A’)B’C’+AB’C=BC+B’C’+AB’C =BC+B’(C’+AC)=BC+B’(C’+A)=BC+B’C’+AB’ Ex 4 -11) Simplify the following Boolean expression (AB +AC)’+A’B’C Sol) (AB)’(AC)’+A’B’C=(A’+B’)(A’+C’)+A’B’C=A’+A’B’ +A’C’+B’C+A’B’C =A’(1+B’+C’+B’C)+B’C=A’+B’C’ Bzu. Pages. COM

Standard Forms of Boolean Expressions • The Sum-of-Products(SOP) Form Ex) AB+ABC, ABC+CDE+B’CD’ • The Product-of-Sums(POS) Form Ex) (A+B)(A+B+C), (A+B+C)(C+D+E)(B’+C+D’) • Principle of Duality : SOP POS • Domain of a Boolean Expression The set of variables contained in the expression Ex) A’B+AB’C : the domain is {A, B, C} Bzu. Pages. COM 33

34 • Implementation of a SOP Expression • Conversion of General Expression to SOP Form AND-OR logic A(B+CD)=AB +ACD Ex 4 -12) Convert each of the following expressions to SOP form: (a) AB+B(CD+EF) (b) (A+B)(B+C+D) Sol) (a) AB+B(CD+EF)=AB+BCD+BEF (b) (A+B)(B+C+D)=AB+AC+AD+ BB+BC+BD =B(1+A+C+D)+ AC+AD=B+AC+AD Bzu. Pages. COM

Standard SOP Form (Canonical SOP Form) 35 For all the missing variables, apply (x+x’)=1 to the AND terms of the expression – List all the min-terms in forms of the complete set of variables in ascending order – Ex 4 -13) Convert the following expression into standard SOP form: AB’C+A’B’+ABC’D Sol) domain={A, B, C, D}, AB’C(D’+D)+A’B’(C’+C)(D’+D)+ABC’D =AB’CD’+AB’CD+A’B’C’D’+A’B’C’D+A’B’CD’+A’B’CD+ABC’D =1010+1011+0000+0001+0010+0011+1101 =0+1+2+3+10+11+13 = (0, 1, 2, 3, 10, 11, 13) Bzu. Pages. COM

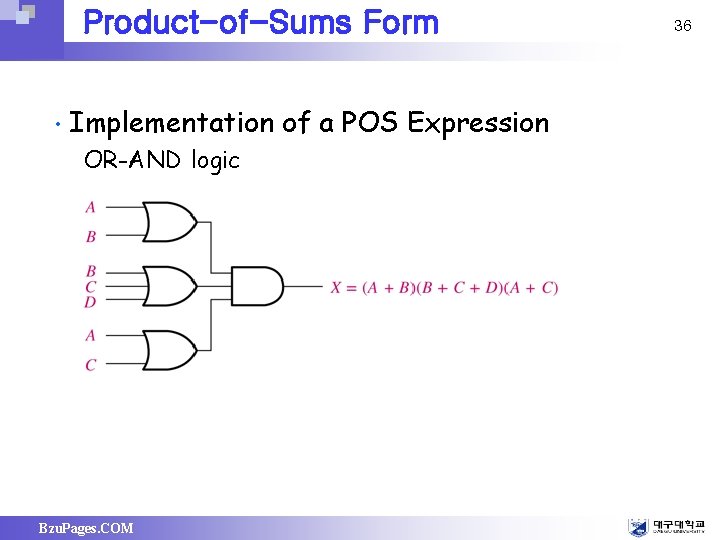
Product-of-Sums Form • Implementation of a POS Expression OR-AND logic Bzu. Pages. COM 36

Standard POS Form (Canonical POS Form) For all the missing variables, apply (x’x)=0 to the OR terms of the expression – List all the max-terms in forms of the complete set of variables in ascending order – Ex 4 -15) Convert the following expression into standard POS form: (A+B’+C)(B’+C+D’)(A+B’+C’+D) Sol) domain={A, B, C, D}, (A+B’+C)(B’+C+D’)(A+B’+C’+D) =(A+B’+C+D’D)(A’A+B’+C+D’)(A+B’+C’+D) =(A+B’+C+D’)(A+B’+C+D)(A’+B’+C+D’)(A +B’+C’+D)=(0100) )(0101)(0110)(1101)= (4, 5, 6, 13) Bzu. Pages. COM 37

Converting Standard SOP to Standard POS 38 Step 1. Evaluate each product term in the SOP expression. Determine the binary numbers that represent the product terms Step 2. Determine all of the binary numbers not included in the evaluation in Step 1 Step 3. Write in equivalent sum term for each binary number Step 2 and expression in POS form Ex 4 -17) Convert the following SOP to POS Sol) SOP= A’B’C’+A’BC+AB’C+ABC=0+2+3+5+7 = (0, 2, 3, 5, 7) POS=(1)(4)(6) = (1, 4, 6) (=(A+B+C’)(A’+B+C)(A’+B’+C)) Bzu. Pages. COM

Boolean Expressions and Truth Tables • Converting SOP Expressions to Truth Table Format Ex 4 -18) A’B’C+AB’C’+ABC = (1, 4, 7) Inputs A B C 0 0 0 1 1 1 0 0 1 1 1 Bzu. Pages. COM Output X 0 1 0 0 1 Product Term A’B’C AB’C’ ABC 39

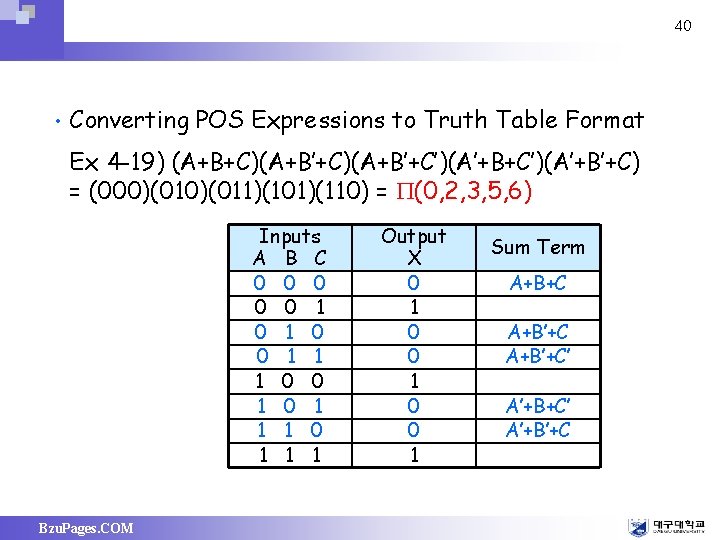
40 • Converting POS Expressions to Truth Table Format Ex 4 -19) (A+B+C)(A+B’+C’)(A’+B’+C) = (000)(011)(101)(110) = (0, 2, 3, 5, 6) Inputs A B C 0 0 0 1 1 1 0 0 1 1 1 Bzu. Pages. COM Output X 0 1 0 0 1 Sum Term A+B+C A+B’+C’ A’+B’+C

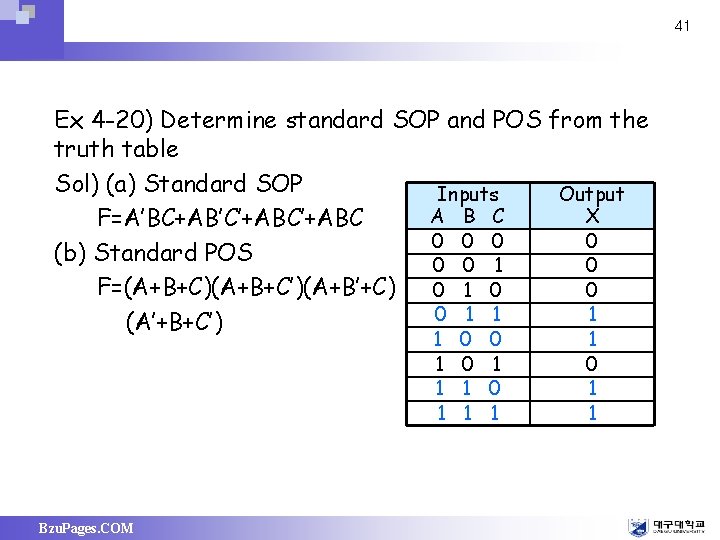
41 Ex 4 -20) Determine standard SOP and POS from the truth table Sol) (a) Standard SOP Inputs Output A B C X F=A’BC+AB’C’+ABC 0 0 (b) Standard POS 0 0 1 0 F=(A+B+C)(A+B+C’)(A+B’+C) 0 1 0 0 0 1 1 1 (A’+B+C’) 1 1 Bzu. Pages. COM 0 0 1 1

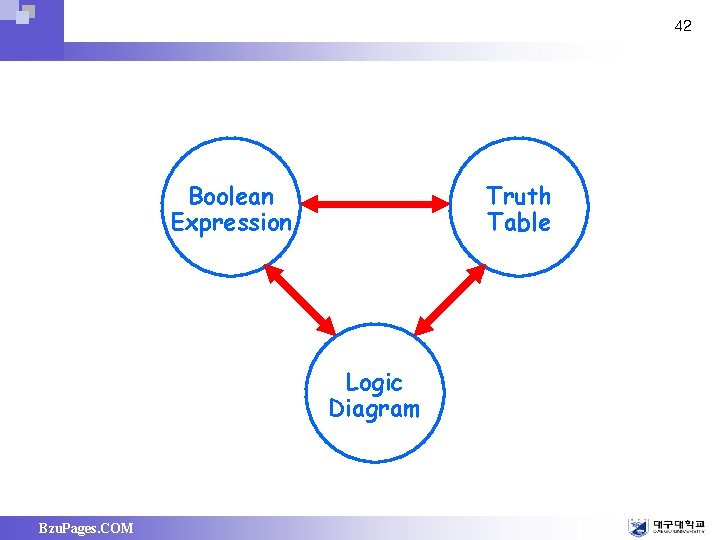
42 Boolean Expression Truth Table Logic Diagram Bzu. Pages. COM

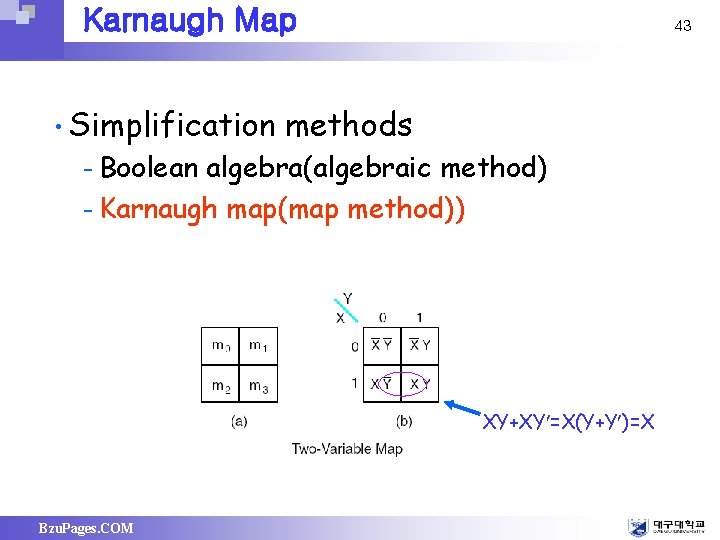
Karnaugh Map • Simplification 43 methods – Boolean algebra(algebraic method) – Karnaugh map(map method)) XY+XY =X(Y+Y )=X Bzu. Pages. COM

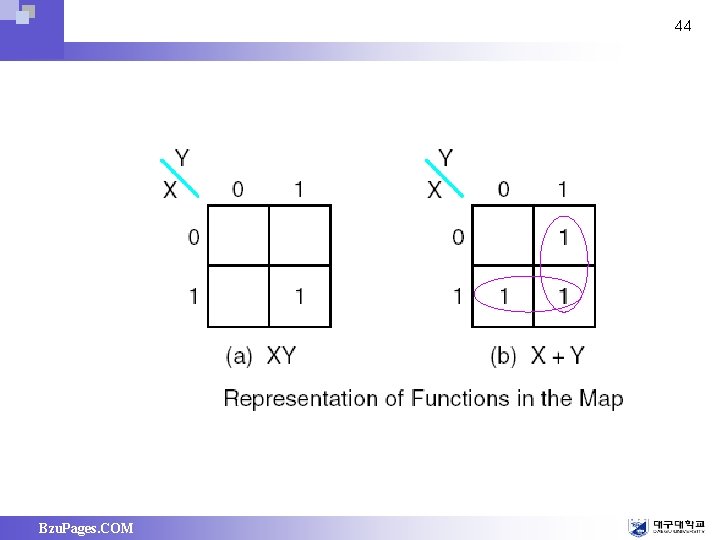
44 Bzu. Pages. COM

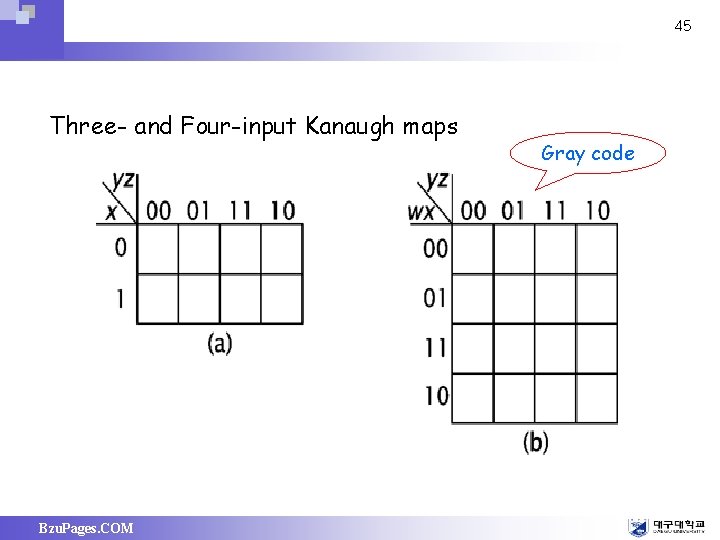
45 Three- and Four-input Kanaugh maps Bzu. Pages. COM Gray code

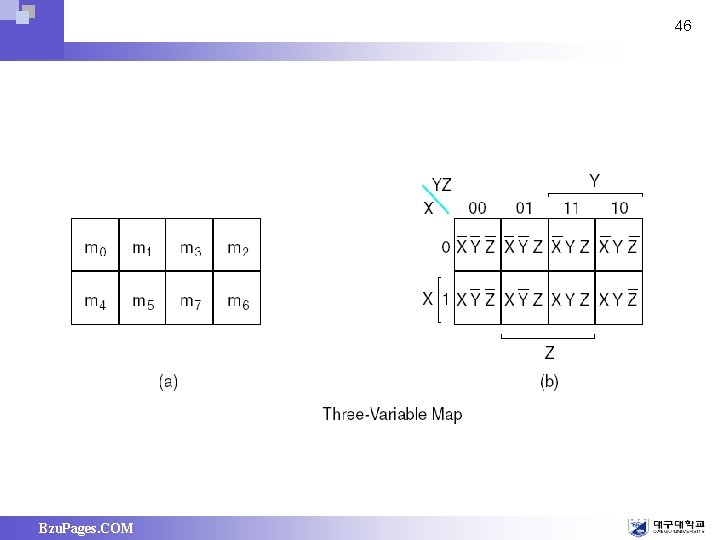
46 Bzu. Pages. COM

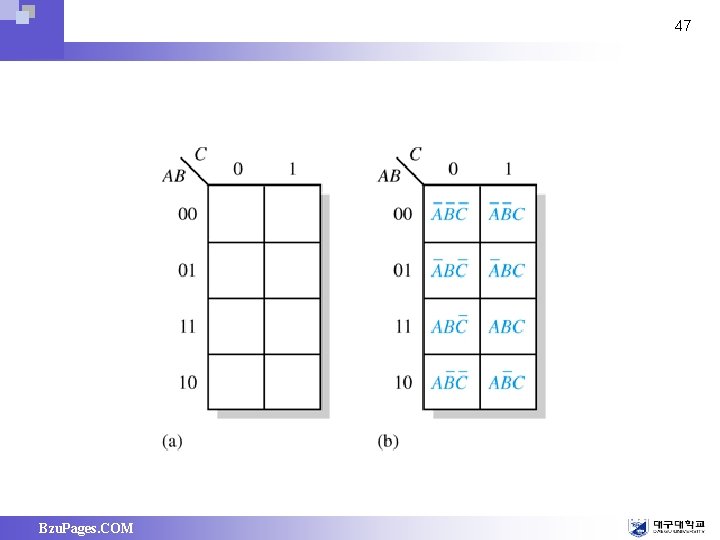
47 Bzu. Pages. COM

48 F(X, Y, Z)= m(0, 1, 2, 6) =(XY +YZ) =X’Y’ + YZ’ Bzu. Pages. COM

49 Example) F(X, Y, Z)= m(2, 3, 4, 5) =X Y+XY Bzu. Pages. COM 0 1 3 2 4 5 7 6

50 Four-Variable Map 16 minterms : m 0 ~ m 15 Rectangle group – 2 -squares(minterms) : 3 -literals product term – 4 -squares : 2 -literals product term – 8 -squares : 1 -literals product term – 16 -squares : logic 1 Bzu. Pages. COM

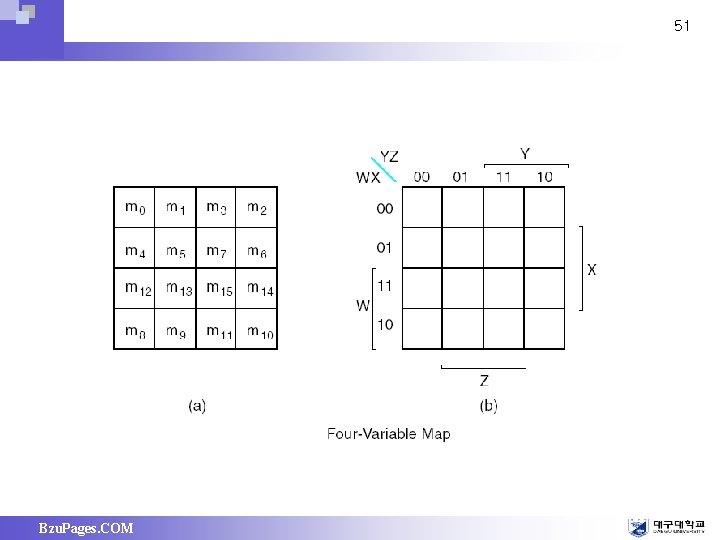
51 Bzu. Pages. COM

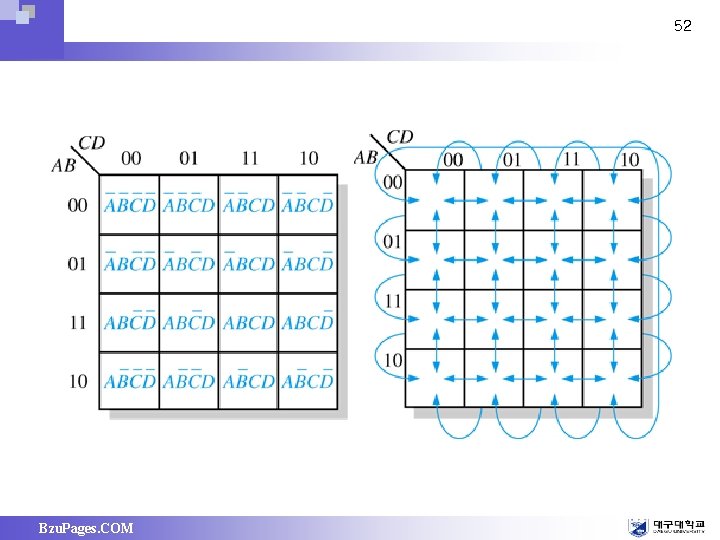
52 Bzu. Pages. COM

53 F(W, X, Y, Z)= m(0, 2, 7, 8, 9, 10, 11) = WX’ + X’Z’ + W’XYZ Bzu. Pages. COM

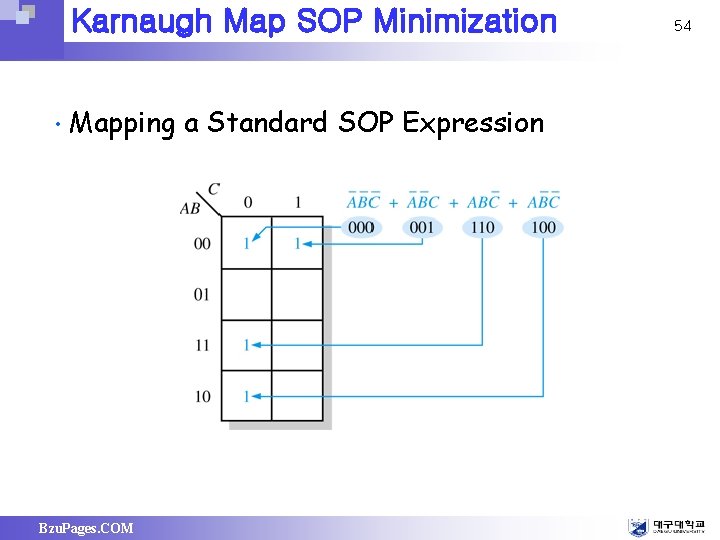
Karnaugh Map SOP Minimization • Mapping a Standard SOP Expression Bzu. Pages. COM 54

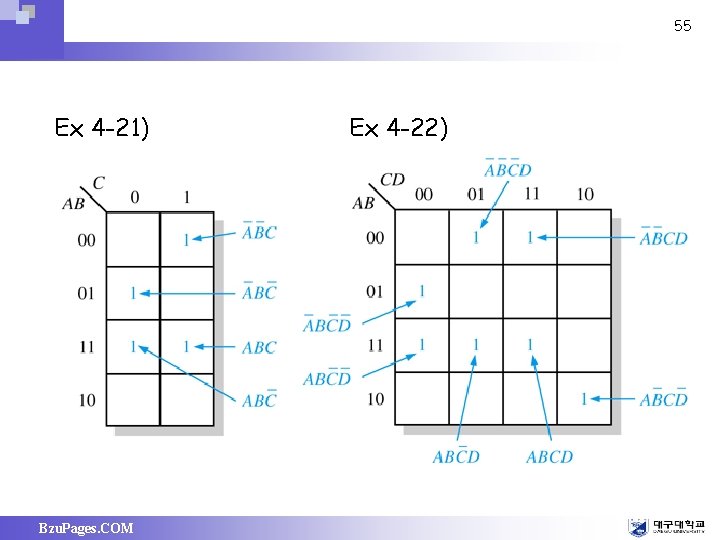
55 Ex 4 -21) Bzu. Pages. COM Ex 4 -22)

56 • Mapping a Nonstandard SOP Expression Numerical Expression of a Nonstandard Product Term Ex 4 -23) A’+ABC’ A’ ABC’ 000 110 001 101 010 011 – Bzu. Pages. COM

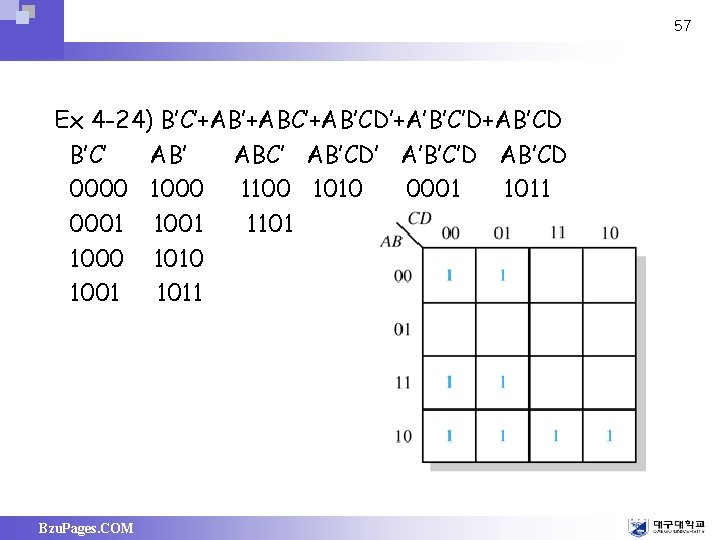
57 Ex 4 -24) B’C’+ABC’+AB’CD’+A’B’C’D+AB’CD B’C’ ABC’ AB’CD’ A’B’C’D AB’CD 0000 1100 1010 0001 1011 0001 1101 1000 1010 1001 1011 Bzu. Pages. COM

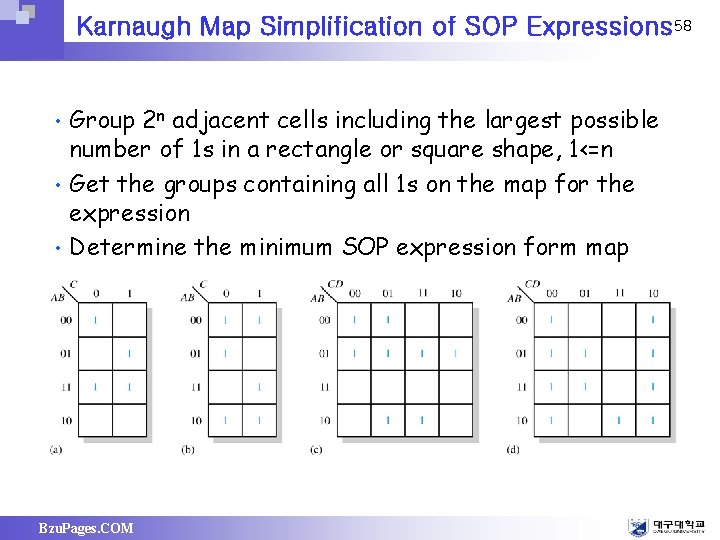
Karnaugh Map Simplification of SOP Expressions 58 • • • Group 2 n adjacent cells including the largest possible number of 1 s in a rectangle or square shape, 1<=n Get the groups containing all 1 s on the map for the expression Determine the minimum SOP expression form map Bzu. Pages. COM

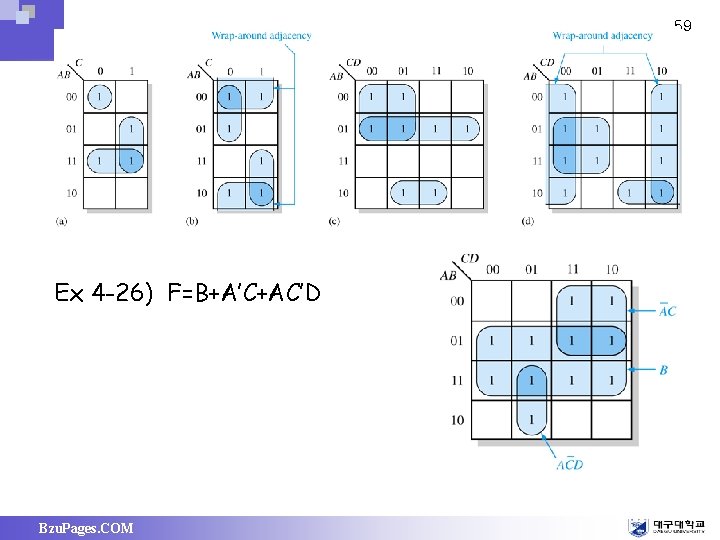
59 Ex 4 -26) F=B+A’C+AC’D Bzu. Pages. COM

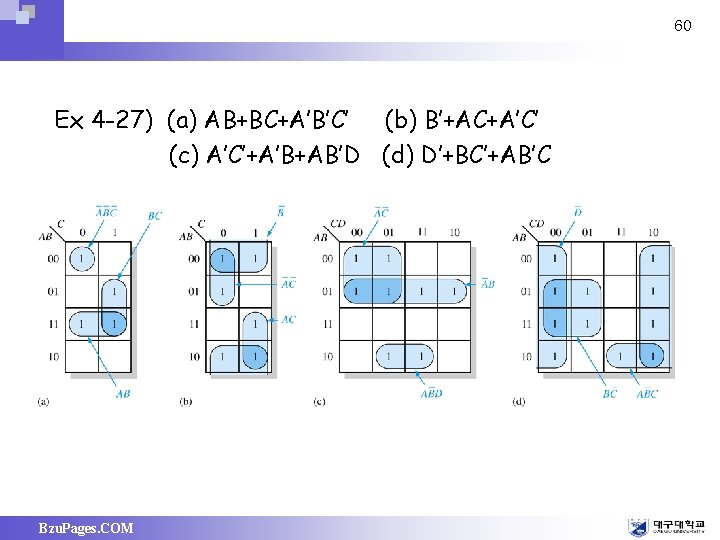
60 Ex 4 -27) (a) AB+BC+A’B’C’ (b) B’+AC+A’C’ (c) A’C’+A’B+AB’D (d) D’+BC’+AB’C Bzu. Pages. COM

61 Ex 4 -28) Minimize the following expression AB’C+A’B’C+A’B’C’+AB’C’ Sol) B’+A’C Bzu. Pages. COM

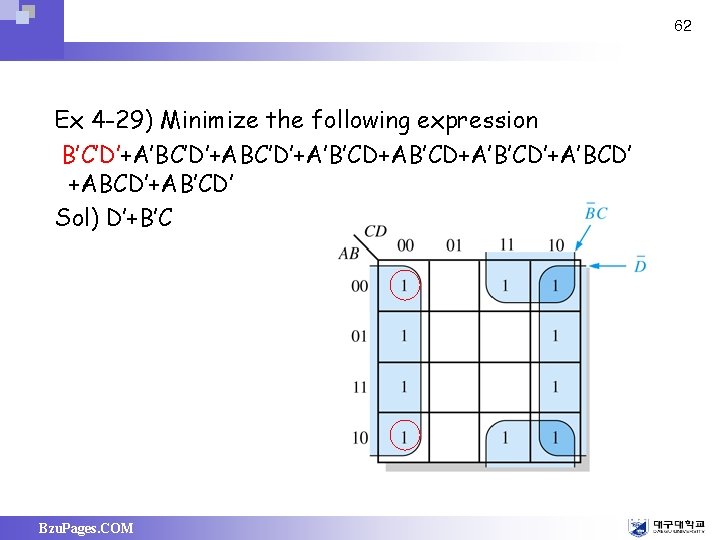
62 Ex 4 -29) Minimize the following expression B’C’D’+A’BC’D’+A’B’CD+A’B’CD’+A’BCD’ +ABCD’+AB’CD’ Sol) D’+B’C Bzu. Pages. COM

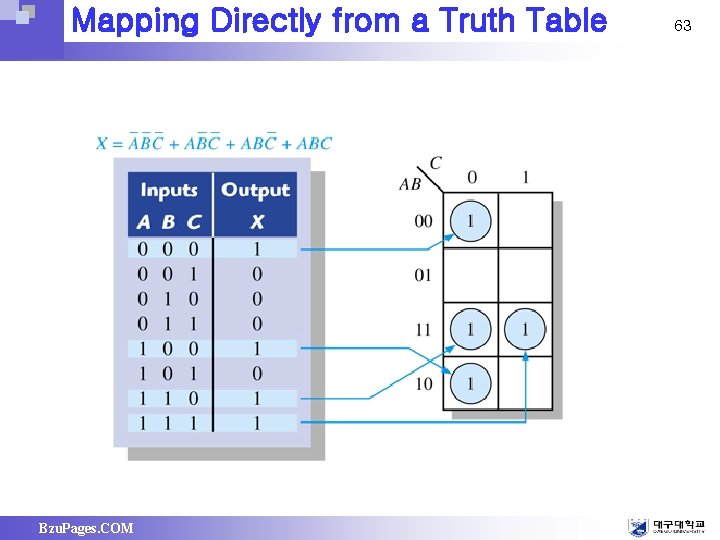
Mapping Directly from a Truth Table Bzu. Pages. COM 63

Don’t Care Conditions • it really does not matter since they will never occur(its output is either ‘ 0’ or ‘ 1’) • The don’t care terms can be used to advantage on the Karnaugh map Bzu. Pages. COM 64

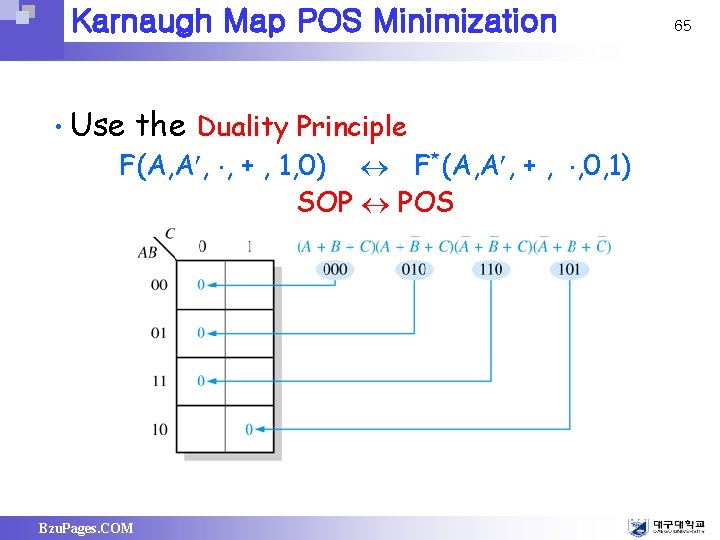
Karnaugh Map POS Minimization • Use the Duality Principle F(A, A , , + , 1, 0) F*(A, A , + , , 0, 1) SOP POS Bzu. Pages. COM 65

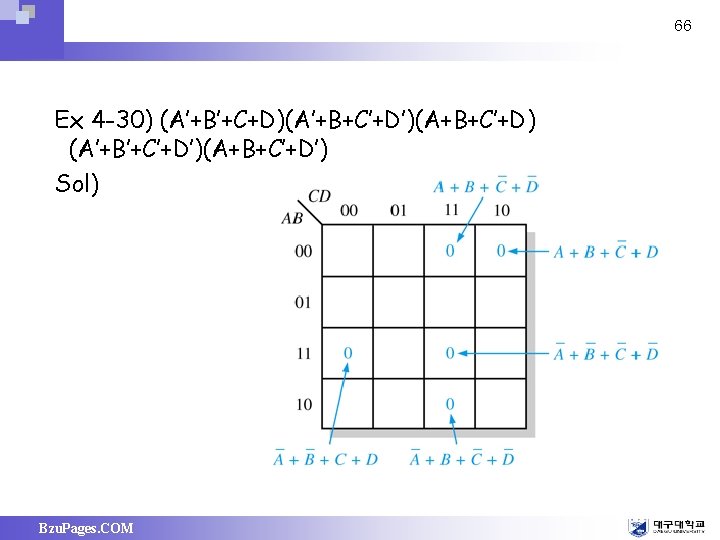
66 Ex 4 -30) (A’+B’+C+D)(A’+B+C’+D’)(A+B+C’+D) (A’+B’+C’+D’)(A+B+C’+D’) Sol) Bzu. Pages. COM

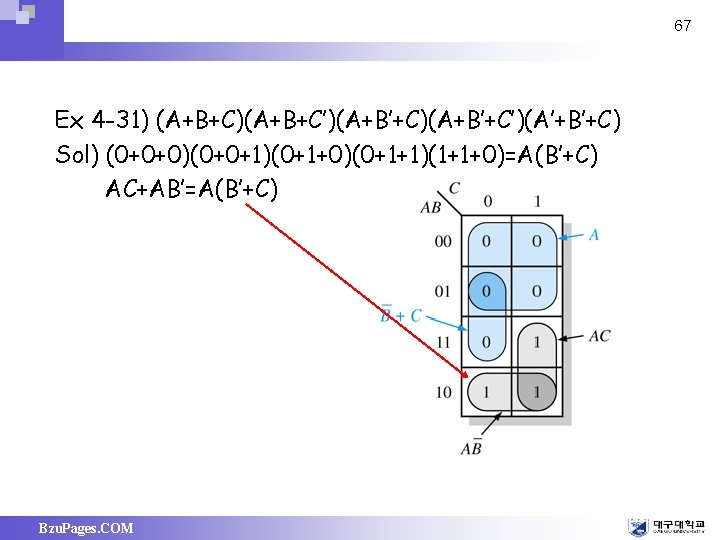
67 Ex 4 -31) (A+B+C)(A+B+C’)(A+B’+C’)(A’+B’+C) Sol) (0+0+0)(0+0+1)(0+1+0)(0+1+1)(1+1+0)=A(B’+C) AC+AB’=A(B’+C) Bzu. Pages. COM

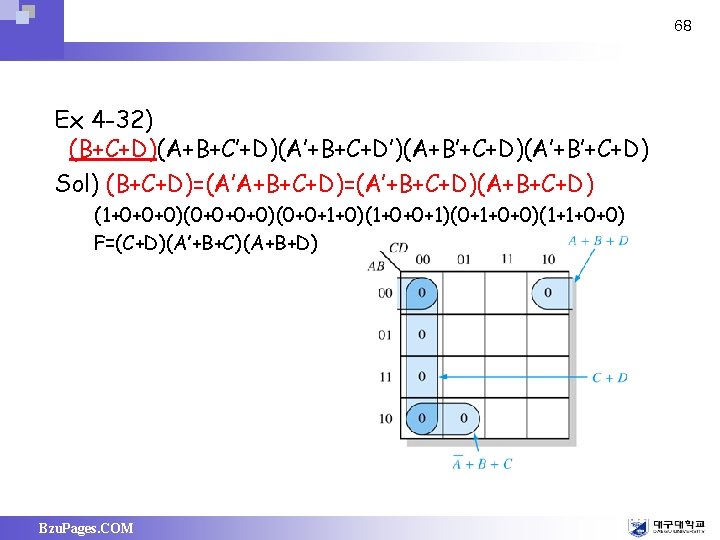
68 Ex 4 -32) (B+C+D)(A+B+C’+D)(A’+B+C+D’)(A+B’+C+D)(A’+B’+C+D) Sol) (B+C+D)=(A’A+B+C+D)=(A’+B+C+D)(A+B+C+D) (1+0+0+0)(0+0+1+0)(1+0+0+1)(0+1+0+0)(1+1+0+0) F=(C+D)(A’+B+C)(A+B+D) Bzu. Pages. COM

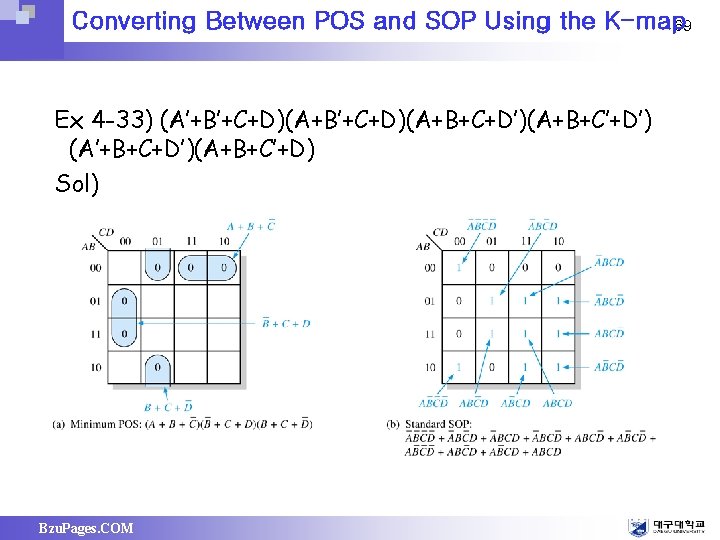
Converting Between POS and SOP Using the K-map 69 Ex 4 -33) (A’+B’+C+D)(A+B+C+D’)(A+B+C’+D’) (A’+B+C+D’)(A+B+C’+D) Sol) Bzu. Pages. COM

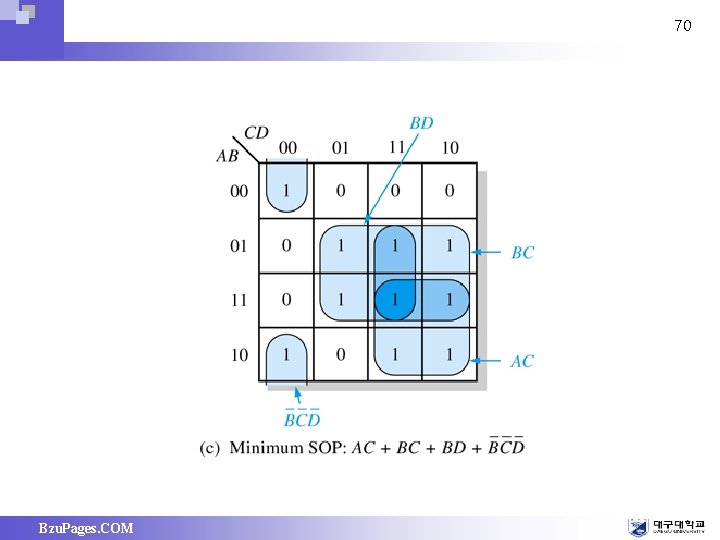
70 Bzu. Pages. COM

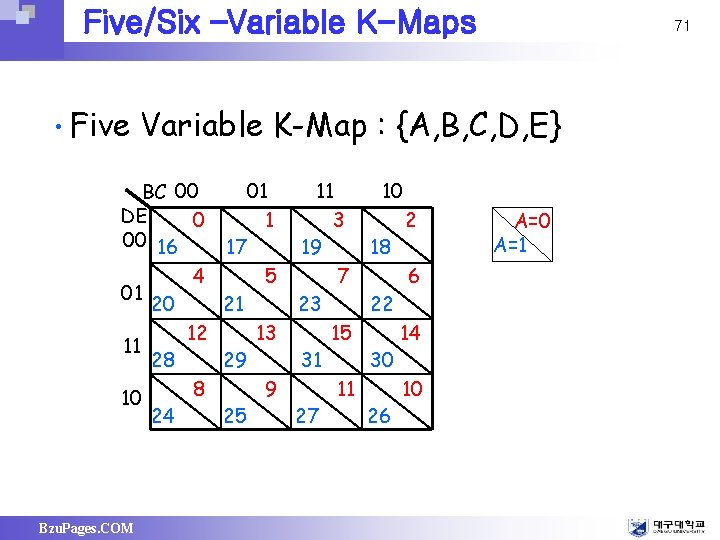
Five/Six –Variable K-Maps • Five Variable K-Map : {A, B, C, D, E} BC 00 DE 0 00 16 01 11 1 3 17 19 4 5 7 01 20 21 23 12 13 15 11 28 29 31 8 9 11 10 24 25 27 Bzu. Pages. COM 71 10 18 22 30 26 2 6 14 10 A=1

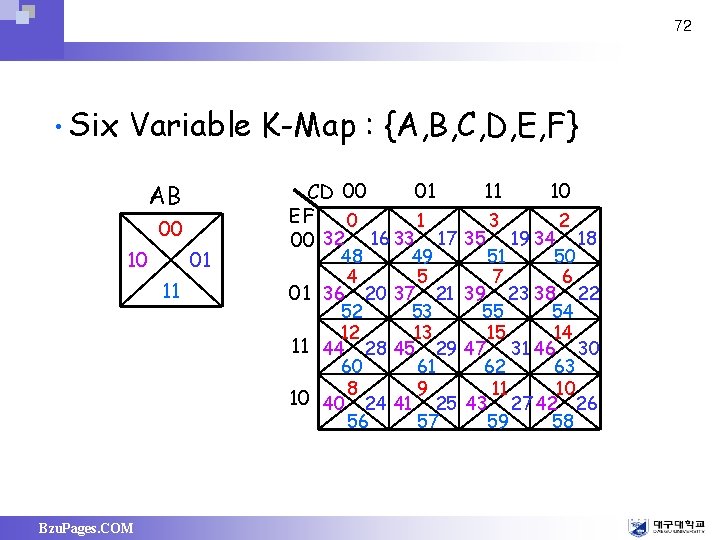
72 • Six Variable K-Map : {A, B, C, D, E, F} AB 00 10 01 11 Bzu. Pages. COM 01 11 10 CD 00 EF 0 1 3 2 00 32 16 33 17 35 19 34 18 48 49 51 50 4 5 7 6 01 36 20 37 21 39 23 38 22 52 53 55 54 12 13 15 14 11 44 28 45 29 47 31 46 30 60 61 62 63 8 9 11 10 10 40 24 41 25 43 27 42 26 56 57 59 58

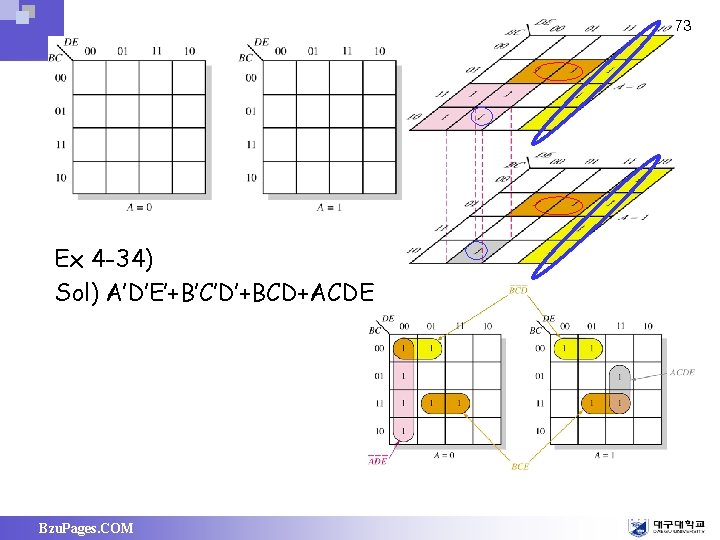
73 Ex 4 -34) Sol) A’D’E’+B’C’D’+BCD+ACDE Bzu. Pages. COM

Digital System Application : 7 -Segment LED Driver Seven-Segment LED driver Bzu. Pages. COM 74

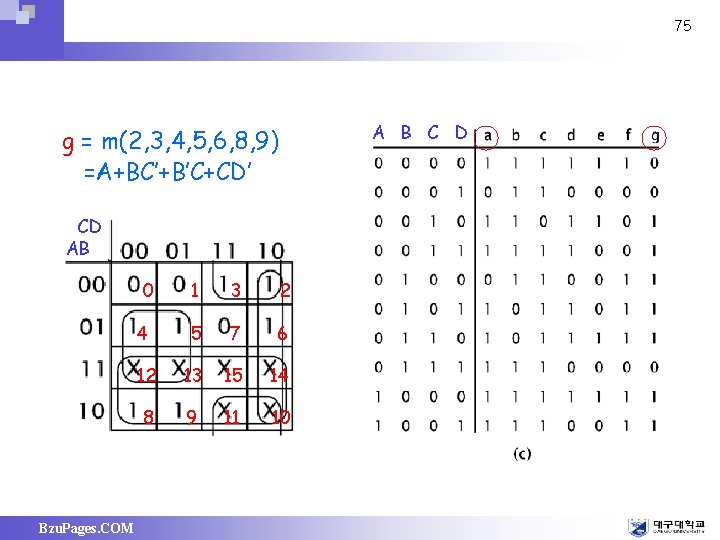
75 A B C D g = m(2, 3, 4, 5, 6, 8, 9) =A+BC’+B’C+CD’ CD AB Bzu. Pages. COM 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10

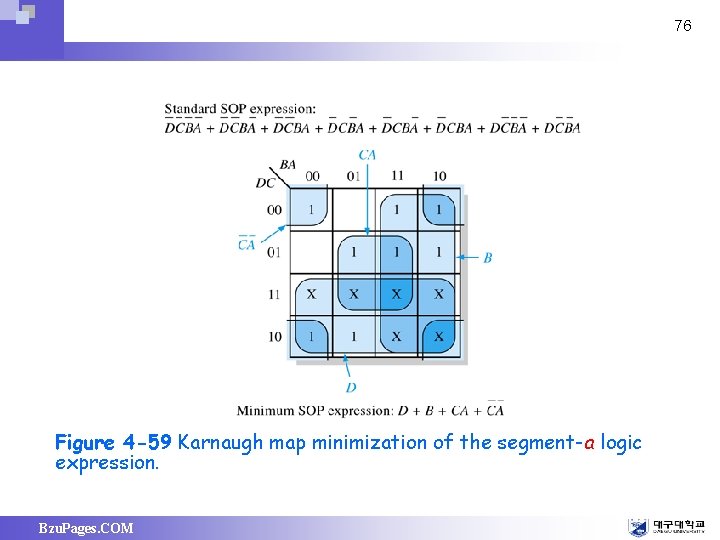
76 Figure 4 -59 Karnaugh map minimization of the segment-a logic expression. Bzu. Pages. COM

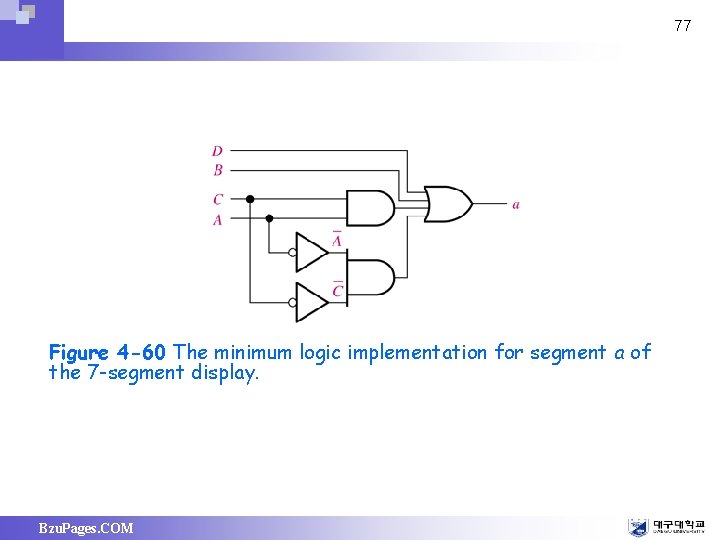
77 Figure 4 -60 The minimum logic implementation for segment a of the 7 -segment display. Bzu. Pages. COM

End of Ch. 4