Ch 3 Inference About Process Quality 1 Sampling

Ch 3 Inference About Process Quality 1. Sampling from a Normal distribution 2. Sampling from a Bernoulli distribution 3. （a）Point Sampling estimator from a Poisson distribution 4. （b）Interval Estimation of process parameterinterval） estimation（confidence 1

1. Sampling from a Normal distribution 假設 ，則 ～ ～ （ with , 其中 ，當 2 時， ）

其中U and V indep. ～ e. g. 其中 and ～ is the sample var. of i. i. d. 回上頁 3

2. Sampling from a Bernoulli distribution i. i. d. Bernoulli with success prob. = p 假設 令 ～ B（n , p） a discrete r. v. with range space 回上頁 4

3. Sampling from a Poisson distribution 假設 i. i. d. ～ a discrete r. v. with taking values 5

令 indep. （e. g. A unit of product can have m different types of defect, each modeled with a Poisson distribution with parameter ） 此稱為 demerit procedure, 若不全為 1, 則L一般未必為Poisson分佈。 回上頁 6

4. Estimation of process parameter （a）Point estimation： Important properties of an estimation （1）Unbiased （2）Minimum variance In general, and are unbiased estimators of the population mean and variance, respectively. 但 S 則一般並非 population standard deviation 的 unbiased estimator. e. g. Poisson ， Binomial 回上頁 7

（b）Interval estimation： [L, U]稱為 的 two sided confidence interval. 稱為 的 one sided confidence interval. 8

e. g. i. i. d. Two sided C. I. or Lower C. I. Upper C. I. 當variance unknown, 則以 S 取代 。 取代 ， two-sided C. I. On the variance 回上頁 9

1. C. I. on the difference in two means （a）Variance known （b）Variance unknown 2. C. I. on the ratio of the variance of two Normal distribution 10

3. C. I. on Binomial parameter （a）If n is large, and , use Normal. （b）If n is small, then use Binomial distribution. （c）If n is large, p is small, then use Poisson. C. I. on the difference of two binomial parameter 11 and .

Hypotheses Testing 1. Null hypotheses 2. Alternative hypotheses 3. Test statistic 4. Rejection region（or critical region） 12

=P(Type I error)=P(reject | is true) （在 Q. C. work, 有時亦可稱為 produce’s risk. ） =P(Type II error)=P(fail to reject | is false) （consumes’s risk） Power=1 - =P(Type II error)=P( reject | is false) Specify and design a test procedure maximize the power （ minimize , a function of sample size. ） p-value = The smallest level of significance that would lead to rejection of the null hypotheses. 13

1. Test on means of normal distribution, variance known v. s. Test statistic or 14

Tests on Means with Known Variance 15

2. Test Means of Normal Distribution, Variance Unknown 16

Test on Binomial Parameter v. s. if if Test on Poisson parameter v. s. 17

Probability of Type II error v. s. 18

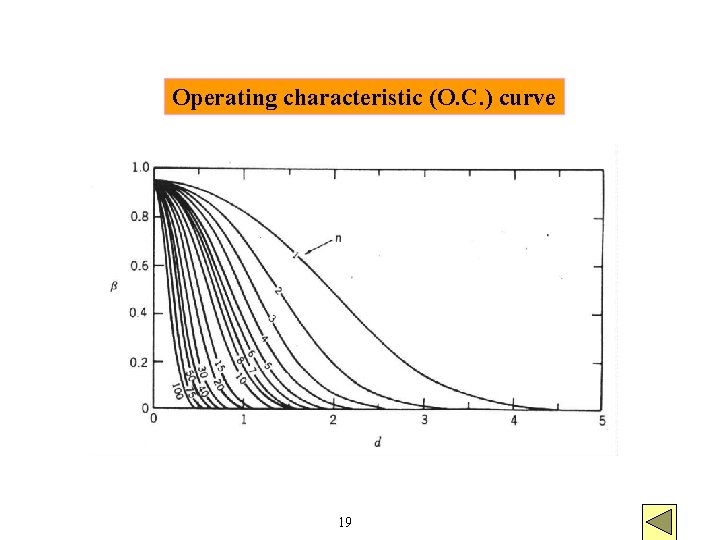
Operating characteristic (O. C. ) curve 19

Tests Means of Normal Distribution, Variance Unknown 3. Paired Data ～ 20

Test on variance of Normal distribution 21