Ch 3 Decision Tree Learning Decision trees Basic

Ch 3. Decision Tree Learning § Decision trees § Basic learning algorithm (ID 3) n Entropy, information gain § Hypothesis space § Inductive bias n Occam’s razor in general § Overfitting problem & extensions n n post-pruning real values, missing values, attribute costs, … 1

Decision Tree for Play. Tennis Outlook Sunny Humidity High No Overcast Rain Yes Normal Yes Wind Strong No Weak Yes 2

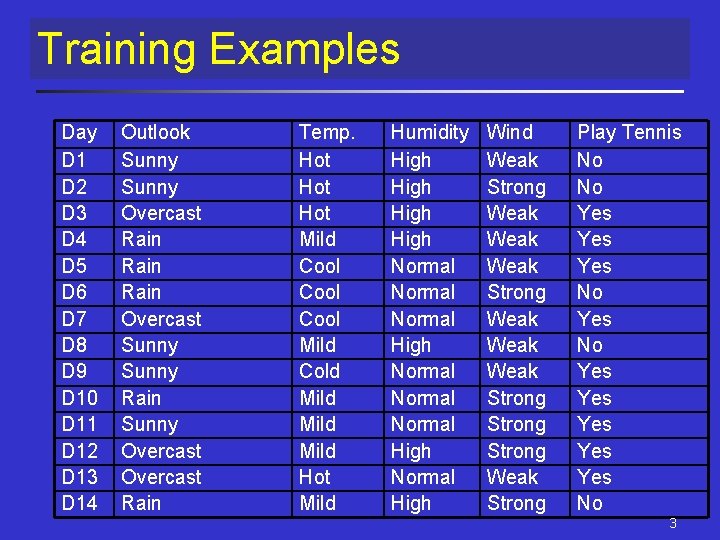
Training Examples Day D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 Outlook Sunny Overcast Rain Overcast Sunny Rain Sunny Overcast Rain Temp. Hot Hot Mild Cool Mild Cold Mild Hot Mild Humidity High Normal Normal High Wind Weak Strong Weak Weak Strong Weak Strong Play Tennis No No Yes Yes Yes No 3

Decision Tree Learning § Classify instances n n n sorting them down the tree to a leaf node containing the class (value) based on attributes of instances branch for each value § Widely used, practical method of approximating discrete-valued functions § Robust to noisy data !! § Capable of learning disjunctive expressions § Typical bias: prefer smaller trees 4

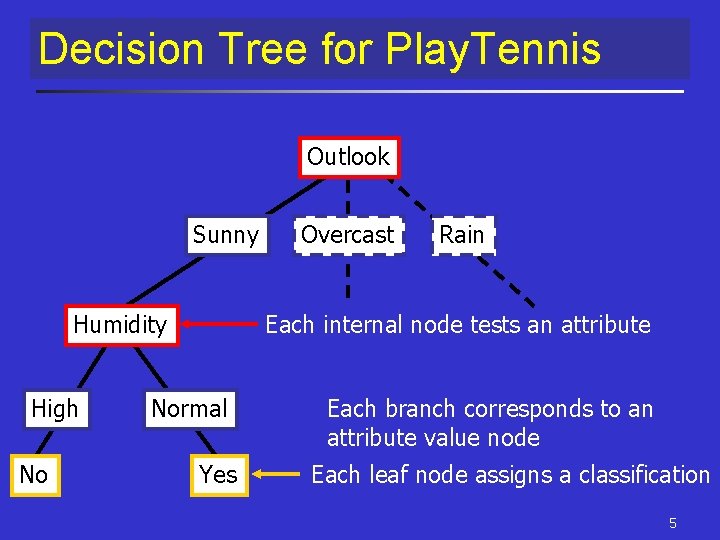
Decision Tree for Play. Tennis Outlook Sunny Humidity High No Overcast Rain Each internal node tests an attribute Normal Yes Each branch corresponds to an attribute value node Each leaf node assigns a classification 5

Decision Tree for Play. Tennis Outlook Temperature Humidity Wind Play. Tennis Sunny Hot High Weak ? No Outlook Sunny Humidity High No Overcast Rain Yes Normal Yes Wind Strong No Weak Yes 6

Decision Tree for Conjunction Outlook=Sunny Wind=Weak Outlook Sunny Wind Strong No Overcast No Rain No Weak Yes 7

Decision Tree for Disjunction Outlook=Sunny Wind=Weak Outlook Sunny Yes Overcast Rain Wind Strong No Wind Weak Yes Strong No Weak Yes 8

Decision Tree for XOR Outlook=Sunny XOR Wind=Weak Outlook Sunny Wind Strong Yes Overcast Rain Wind Weak No Strong No Wind Weak Yes Strong No Weak Yes 9

Decision Tree • decision trees represent disjunctions of conjunctions Outlook Sunny Humidity High No Overcast Rain Yes Normal Yes Wind Strong No Weak Yes (Outlook=Sunny Humidity=Normal) (Outlook=Overcast) (Outlook=Rain Wind=Weak) 10

When to use Decision Trees? § Instances presented as attribute-value pairs § Target function has discrete values n classification problems § Disjunctive descriptions required n disjunction of conjunctions of constraints on attribute values of instances § Training data may contain n n errors missing attribute values § Examples: n n n Medical diagnosis Credit risk analysis Object classification for robot manipulator 11

Top-Down Induction of Decision Trees - ID 3 1. A the “best” decision attribute for next 2. 3. 4. 5. node Assign A as decision attribute for node For each value of A create new descendant Sort training examples to leaf nodes according to the attribute value of the branch If all training examples are perfectly classified (same value of target attribute) stop, else iterate over new leaf nodes. 12

Which Attribute is ”best”? [29+, 35 -] A 1=? True [21+, 5 -] A 2=? [29+, 35 -] False [8+, 30 -] True [18+, 33 -] False [11+, 2 -] 13

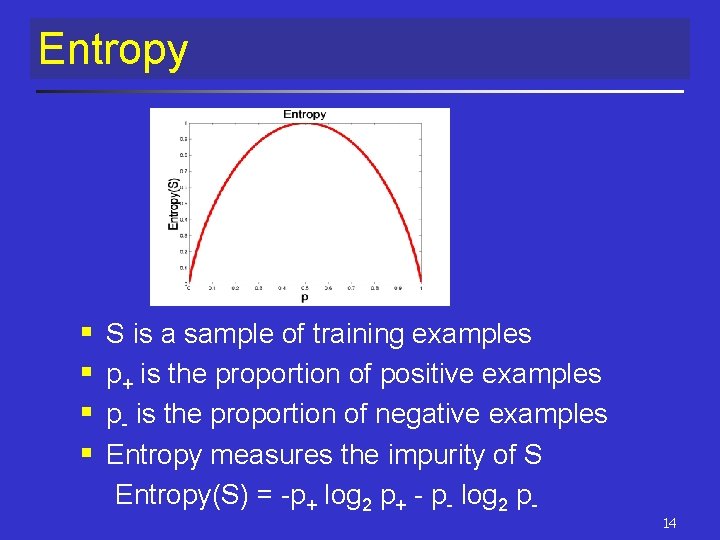
Entropy § § S is a sample of training examples p+ is the proportion of positive examples p- is the proportion of negative examples Entropy measures the impurity of S Entropy(S) = -p+ log 2 p+ - p- log 2 p- 14

Entropy § Entropy(S)= expected number of bits needed to encode class (+ or -) of randomly drawn members of S (under the optimal, shortest lengthcode) § Why? § Information theory optimal length code assign –log 2 p bits to messages having probability p. § So the expected number of bits to encode (+ or -) of random member of S: -p+ log 2 p+ - p- log 2 p 15

Information Gain § Gain(S, A): expected reduction in entropy due to sorting S on attribute A Gain(S, A)=Entropy(S) - v values(A) |Sv|/|S| Entropy(Sv) Entropy([29+, 35 -]) = -29/64 log 2 29/64 – 35/64 log 2 35/64 = 0. 99 [29+, 35 -] A 1=? True [21+, 5 -] A 2=? [29+, 35 -] False [8+, 30 -] True [18+, 33 -] False [11+, 2 -] 16

Information Gain Entropy([21+, 5 -]) = 0. 71 Entropy([8+, 30 -]) = 0. 74 Gain(S, A 1)=Entropy(S) -26/64*Entropy([21+, 5 -]) -38/64*Entropy([8+, 30 -]) =0. 27 Entropy([18+, 33 -]) = 0. 94 Entropy([8+, 30 -]) = 0. 62 Gain(S, A 2)=Entropy(S) -51/64*Entropy([18+, 33 -]) -13/64*Entropy([11+, 2 -]) =0. 12 [29+, 35 -] A 1=? True [21+, 5 -] A 2=? [29+, 35 -] False [8+, 30 -] True [18+, 33 -] False [11+, 2 -] 17

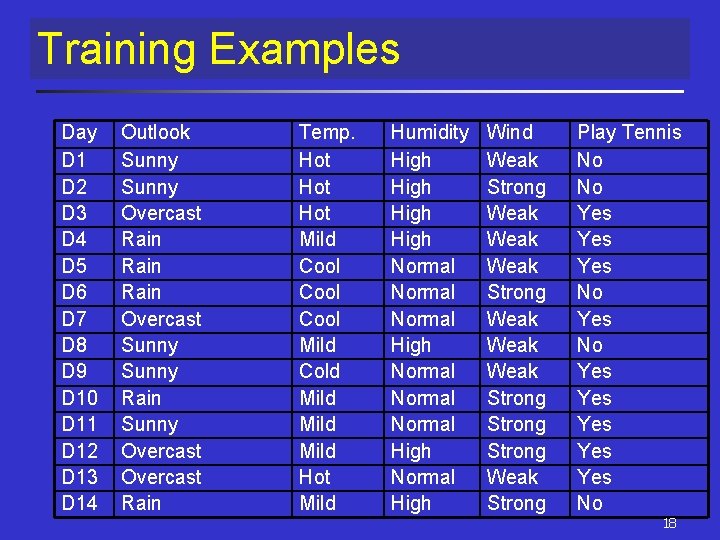
Training Examples Day D 1 D 2 D 3 D 4 D 5 D 6 D 7 D 8 D 9 D 10 D 11 D 12 D 13 D 14 Outlook Sunny Overcast Rain Overcast Sunny Rain Sunny Overcast Rain Temp. Hot Hot Mild Cool Mild Cold Mild Hot Mild Humidity High Normal Normal High Wind Weak Strong Weak Weak Strong Weak Strong Play Tennis No No Yes Yes Yes No 18

Selecting the Best Attribute S=[9+, 5 -] E=0. 940 Humidity Wind High [3+, 4 -] E=0. 985 Normal [6+, 1 -] E=0. 592 Gain(S, Humidity) =0. 940 -(7/14)*0. 985 – (7/14)*0. 592 =0. 151 Weak [6+, 2 -] Strong [3+, 3 -] E=0. 811 E=1. 0 Gain(S, Wind) =0. 940 -(8/14)*0. 811 – (6/14)*1. 0 =0. 048 19

Selecting the Best Attribute S=[9+, 5 -] E=0. 940 Outlook Sunny Over cast Rain [2+, 3 -] [4+, 0] [3+, 2 -] E=0. 971 E=0. 0 E=0. 971 Gain(S, Outlook) =0. 940 -(5/14)*0. 971 -(4/14)*0. 0 – (5/14)*0. 971 =0. 247 20

ID 3 Algorithm [D 1, D 2, …, D 14] [9+, 5 -] Outlook Sunny Overcast Rain Ssunny=[D 1, D 2, D 8, D 9, D 11] [D 3, D 7, D 12, D 13] [D 4, D 5, D 6, D 10, D 14] [2+, 3 -] [4+, 0 -] [3+, 2 -] ? Yes ? Gain(Ssunny , Humidity)=0. 970 -(3/5)0. 0 – 2/5(0. 0) = 0. 970 Gain(Ssunny , Temp. )=0. 970 -(2/5)0. 0 – 2/5(1. 0)-(1/5)0. 0 = 0. 570 Gain(Ssunny , Wind)=0. 970= -(2/5)1. 0 – 3/5(0. 918) = 0. 019 21

ID 3 Algorithm Outlook Sunny Humidity High No [D 1, D 2] Overcast Rain Yes [D 3, D 7, D 12, D 13] Normal Yes [D 8, D 9, D 11] Wind Strong Weak No Yes [D 6, D 14] [D 4, D 5, D 10] 22

Hypothesis Space Search ID 3 + - + A 2 A 1 + - + - + + - - - + A 2 - A 3 + - A 2 - + - + A 4 23

Hypothesis Space Search ID 3 § Hypothesis space is complete! Target function surely in there… Outputs a single hypothesis No backtracking on selected attributes (greedy search) n Local minimal (suboptimal splits) Statistically-based search choices n Robust to noisy data Inductive bias (search bias) n Prefer shorter trees over longer ones n Place high info. gain attributes close to the root n § § 24

Inductive Bias in ID 3 § H is the power set of instances X Unbiased ? § Preference for short trees, and for those with high information gain attributes near the root § Bias is a preference for some hypotheses, rather than a restriction of the hypothesis space H § Compare bias to C-E n n n ID 3: complete space, incomplete search --> bias from search strategy C-E: incomplete space, complete search --> bias from expressive power of H 25

Occam’s Razor § Why prefer short hypotheses? § Argument in favor: n n n Fewer short hypotheses than long hypotheses A short hypothesis that fits the data is unlikely to be a coincidence A long hypothesis that fits the data might be a coincidence § Argument against: n n n There are many ways to define small sets of hypotheses E. g. All trees with a prime number of nodes that use attributes beginning with ”Z” What is so special about small sets based on size of hypothesis? ? ? 26

Overfitting - definition § Consider error of hypothesis h over n n Training data: errortrain(h) Entire distribution D of data: error. D(h) § Hypothesis h H overfits training data if there is an alternative hypothesis h’ H such that errortrain(h) < errortrain(h’) and error. D(h) > error. D(h’) § Possible reasons: noise and small samples n n n coincidences possible with small samples noisy data creates a large tree h h’ not fitting it is likely to work better 27

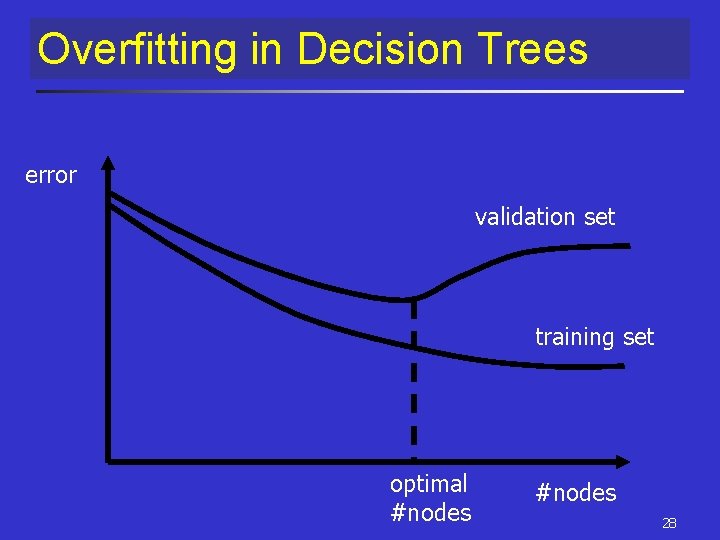
Overfitting in Decision Trees error validation set training set optimal #nodes 28

Avoid Overfitting How can we avoid overfitting? § Stop growing when data split not statistically significant § Grow full tree then post-prune n has been found more successful § Minimum description length (MDL): Minimize: size(tree) + size(misclassifications(tree)) 29

How to decide tree size? § What criterion to use n n n separate test set to evaluate the use of pruning use all data, apply statistical test to estimate if expanding/pruning is likely to produce improvement use an explicit complexity measure (coding length of data & tree), stop growth when minimized 30

Training/validation sets § Available data split n n n training set: apply learning to this validation set: evaluate result § accuracy § impact of pruning § ‘safety check’ against overfit common strategy: 2/3 for training 31

Reduced error pruning § Pruning n n make an inner node a leaf node assign it the most common class § Procedure Split data into training and validation set Do until further pruning is harmful: 1. Evaluate impact on validation set of pruning each possible node (plus those below it) 2. Greedily remove the one that most improves the validation set accuracy § Produces smallest version of most accurate subtreee 32

Rule Post-Pruning § Procedure (C 4. 5 uses a variant) n n n infer DT as usual (allow overfit) convert tree to rules (one per path) prune each rule independently § remove preconditions if result is more accurate n n sort rules by estimated accuracy into a desired sequence to use apply rules in this order in classification 33

Rule post-pruning… § Estimating the accuracy n n separate validation set training data & pessimistic estimates § data is too favorable for the rules § compute accuracy & standard deviation § take lower bound from given confidence level (e. g. 95%) as the measure § very close to observed one for large sets § not statistically valid but works 34

Why convert to rules? § Distinguishing different contexts in which a node is used n separate pruning decision for each path § No difference for root/inner n no bookkeeping on how to reorganize tree if root node is pruned § Improves readability 35

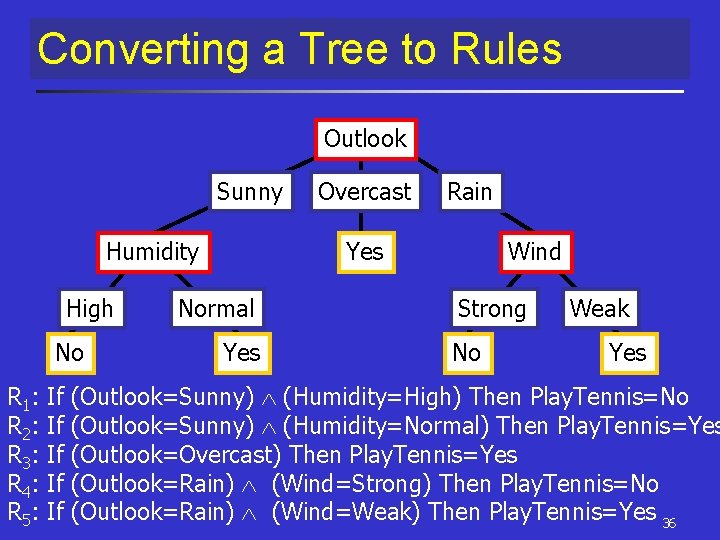
Converting a Tree to Rules Outlook Sunny Humidity High No R 1: R 2: R 3: R 4: R 5: If If If Overcast Rain Yes Normal Yes Wind Strong No Weak Yes (Outlook=Sunny) (Humidity=High) Then Play. Tennis=No (Outlook=Sunny) (Humidity=Normal) Then Play. Tennis=Yes (Outlook=Overcast) Then Play. Tennis=Yes (Outlook=Rain) (Wind=Strong) Then Play. Tennis=No (Outlook=Rain) (Wind=Weak) Then Play. Tennis=Yes 36

Continuous values § Define new discrete-valued attr n partition the continuous value into a discrete set of intervals § Ac = true iff A < c § How to select best c? (inf. gain) § Example case n n sort examples by continuous value identify borderlines Temperature 150 C 180 C 190 C 220 C 240 C 270 C Play. Tennis No Yes Yes No 37

Continuous values… § Fact n value maximizing inf. gain lies on such boundary § Evaluation n compute gain for each boundary § Extensions n n multiple values LTUs based on many attributes 38

Alternative selection measures § Information gain measure favors attributes with many values n n n separates data into small subsets high gain, poor prediction E. g. : Imagine using Date=xx. yy. zz as attribute § perfectly splits the data into subsets of size 1 § Use gain ratio instead of information gain!! n n penalize gain with split information sensitive to how broadly & uniformly attribute splits data § Entropy of S with respect to values of A n earlier: entropy of S w. r. t target values 39

Split information § Gain. Ratio(S, A) = Gain(S, A) / Split. Info (S, A) n n Split. Info(S, A) = - i=1. . c |Si|/|S| log 2 |Si|/|S| Where Si is the subset for which attribute A has the value vi § Discourages selection of attr with n n many uniformly distr. Values n values: log n, boolean: 1 § Better to apply heuristics to select attributes n n compute Gain first compute GR only when Gain large enough (above average) 40

Another alternative § Distance-based measure n n n define a metric between partitions of the data evaluate attributes: distance between created & perfect partition choose the attribute with closest one § Shown n not biased towards attr. with large value sets § Many alternatives like this in the literature. 41

Missing values § Estimate value n other examples with known value § Compute Gain(S, A), A(x) unknown n assign most common value in S most common with class c(x) assign probability for each value, distribute fractionals of x down § Similar techniques in classification 42

Attributes with differing costs § Measuring attribute costs something n n prefer cheap ones if possible use costly ones only if good gain introduce cost term in selection measure no guarantee in finding optimum, but give bias towards cheapest § Replace Gain by : Gain 2(S, A)/Cost(A) § Example applications n n robot & sonar: time required to position medical diagnosis: cost of a laboratory test 43

Summary § Decision-tree induction is a popular approach to classification that enables us to interpret the output hypothesis § Practical learning method n n § § § discrete-valued functions ID 3: top-down greedy algorithm Complete hypothesis space Preference bias - shorter trees preferred. Overfitting is an important issue n n Reduced error pruning Rule post-pruning § Techniques exist to deal with continuous attributes and missing attribute values. 44