CH 2 The Meaning of the Constitutive Equation

CH 2 The Meaning of the Constitutive Equation Prof. M. -S. Ju Dept. of Mechanical Eng. National Cheng Kung University

2. 1 Introduction Living system at cellular, tissue, organ and organism level sufficient to take Newton’s laws of motion as axiom The smallest volume considered contains a very large no. of atoms and molecules. The materials can be considered as a continuum Isomorphism between real number and material particles. Between any two material particles there is another material particle.

Continuum: in Euclidean space, between any two material particles there is another material particle, each material particle has a mass. Mass density of a continuum at a point P is defined as: P DV DM

Modification of definition Observation of living organisms at various levels of size: e. g. , naked eye, optical microscope, electrical microscope, scanning tunnel microscope or atomic force microscope

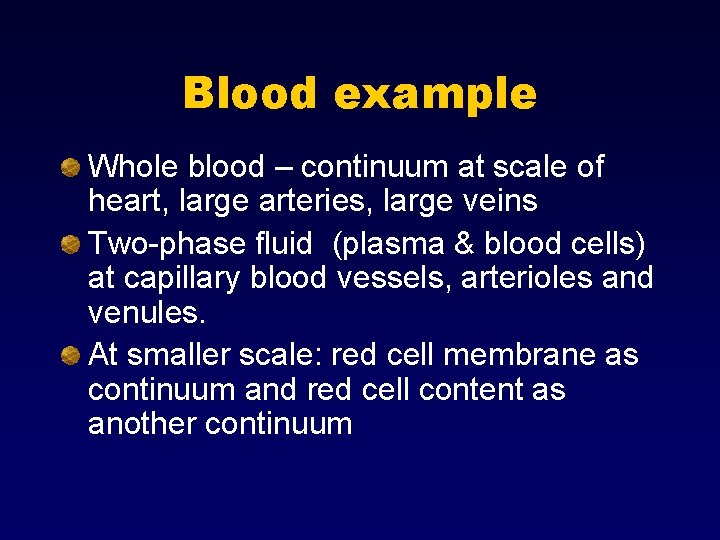
Blood example Whole blood – continuum at scale of heart, large arteries, large veins Two-phase fluid (plasma & blood cells) at capillary blood vessels, arterioles and venules. At smaller scale: red cell membrane as continuum and red cell content as another continuum

2. 2 Stress expresses the interaction of the material in one part of the body on another. Unit: 1 Pa = 1 N/m 2 1 psi = 6. 894 k. Pa 1 dyn/cm 2 = 0. 1 Pa 1 atmosphere = 1. 013 x 105 N/m 2 = 1. 013 bar

Assume that as DS tends to zero the ratio DF/DS tends to a definite limit, d. F/ds, and moment of the force acting on the surface DS tends to zero. DF Stress n x 3 DS S B o x 1 x 2

Let vector n be normal of DS Positive side: surface pointed by n Positive side exerts force DF on the negative side DF depends on location and size of DS and orientation of n When DS→ 0 moment of DF exerts on DS → 0 force per unit area acting on the surface

Components of stress x 3 t t 33 t 32 n tt t t 31 23 13 12 22 21 11 o x 1 ds x 2

Note: knowing components of a stress tensor one can write down the stress vector acting on any surface with unit outer normal vector n

(2) For a body in equilibrium we have Xi: components of body force (per unit volume) along ith axis Due to equilibrium of moments

(4) change of coordinate system t’km components of stress tensor in the new coordinate system tij components of stress tensor in theold coordinate system

2. 3 Strain Deformation of a solid described by strain Take one-dimensional problem as an example: elongation of a string, initial length L 0

Other definitions: Note: above strain measures are equal for infinitesimal elongation

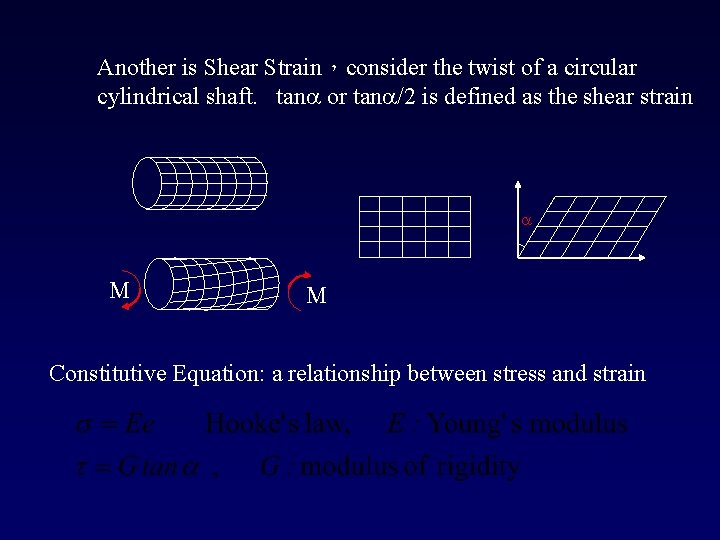
Another is Shear Strain，consider the twist of a circular cylindrical shaft. tana or tana/2 is defined as the shear strain a M M Constitutive Equation: a relationship between stress and strain

Deformation of living system is more complicated and require a general method. Let a body occupy a space S，let coordinate of a particle before deformation be (a 1, a 2, a 3)，coordinate after deformation(x 1, x 2, x 3)， a 3 , x 3 P’ P” P S a 1, x 1 u Q” Q’ Q (a 1, a 2, a 3) o Q: stretching and distortion of the body? a 2, x 2 (x 1, x 2, x 3)

After the deformation p and p’ displaced to Q and Q’，QQ’ distance d. S

Definition of strain tensors: Show that Eij and eij are symmetric

When ui is small eij reduces to Cauchy’s infinitesimal strain tensor: Cauchy strain tensor

or In the infinitesimal deformation, no distinction between Lagrangian and Eulerian strain tensors.

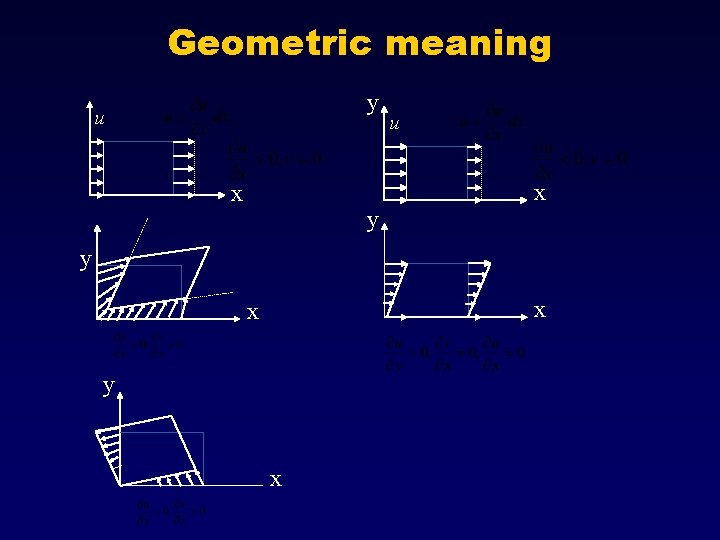
Geometric meaning y u x y x

2. 4 Strain rate For fluid motion, consider velocity field and rate of strain. At point (x, y, z) velocity vector For continuous flow, Vi : continuous and differentiable

Define strain rate tensor Vij Define vorticity tensor Wij

2. 5 Constitutive equations Properties of materials are specified by constitutive equations Non-viscous fluid, Newtonian viscous fluid and Hookean elastic solid are most widely models for engineering materials Most biological materials can not be described by above equations Constitutive equations are independent of any particular set of coordinates. A constitutive equation must be a tensor equation: every term in it be a tensor of same rank.

2. 6 The Nonviscous Fluid Stress tensor: D Kronecker delta, p: pressure (scalar) For ideal gas: equation of state For real gas: f (p, r, T) = 0 Incompressible fluid: r = constant

2. 7 Newtonian Viscous Fluid Shear stress is proportional to strain rate Stress-strain rate relationship sij : stress tensor, Vkl: strain rate tensor, p: static pressure • p= p(r, T) equation of state • Elements of Dijkl depend on temperature but stress or strain rate • Isotropic materials: a tensor has same array of components when frame of reference is rotated or reflected (isotropic tensor)

Coefficient of viscosity m Newton proposed Units: 1 poise= dyne. s /cm 2 = 0. 1 Ns/m 2 Viscosity of air: 1. 8 x 10 -4 poise Water: 0. 01 poise at 1 Atm. 20 deg C Glycerin: 8. 7 poise

2. 8 Hookean Elastic Solid Hooke’s law: stress tensor linearly proportional to strain tensor Note: elastic moduli are independent of stress or strain

Isotropic materials

Inverted form

E: Young’s modulus, G: shear modulus, n: Poisson’s ratio

2. 9 Effect of Temperature The constitutive equations are stated at a given temperature T 0 Dijkl, Cijkl, m depend on temperature If temperature is variable: Duhamel-Neumann form

For isotropic material a: linear expansion coefficient

2. 10 Materials with more complex mechanical behavior In limited ranges of temperature, stress and strain, some real materials may follow above constitutive equations Real materials have more complex behavior: l Non-Newtonian fluids: blood, paints and varnish, wet clay and mud, colloidal solutions l Hookean elastic solid: structural material within elastic limit, disobey Hooke’s law for yielding & fracture l Few biological tissues obey Hooke’s law

2. 11 Viscoelasticity Features: hysteresis, relaxation, creeping Stress Relaxation l Body is suddenly strained and maintained constant, the corresponding stress decreases with time Creep l Body is suddenly stressed and maintained constant, the body continues to deform Hysteresis l Body subjected to cyclic loading, the stress-strain relationship is different between loading cycle and unloading cycle.

Mechanical Models of Viscoelastic Materials Maxwell model (series) Voigt model (parallel) Kelvin model (standard linear solid) (series + parallel) Lumped mass model consisted of linear springs and dashpots spring constant: m viscous coefficient of dashpot: h

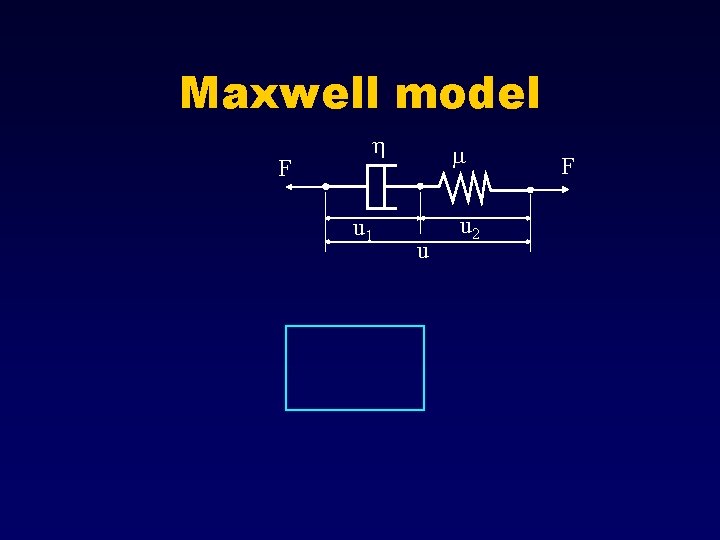
Maxwell model F h u 1 m u u 2 F

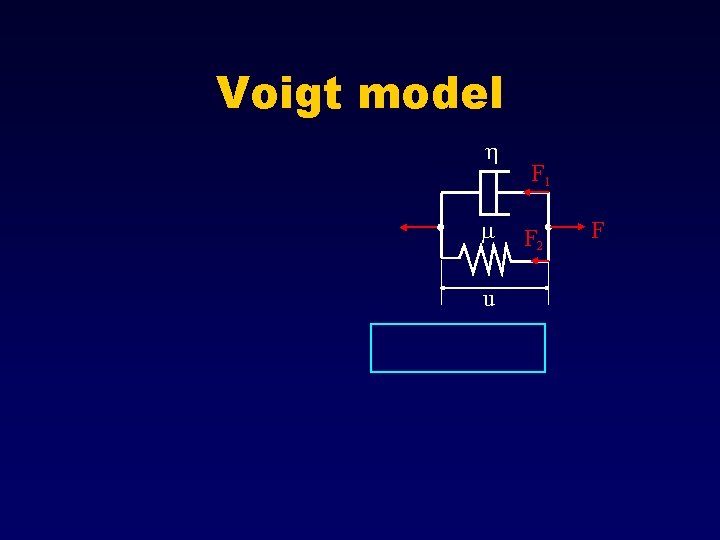
Voigt model h m u F 1 F 2 F

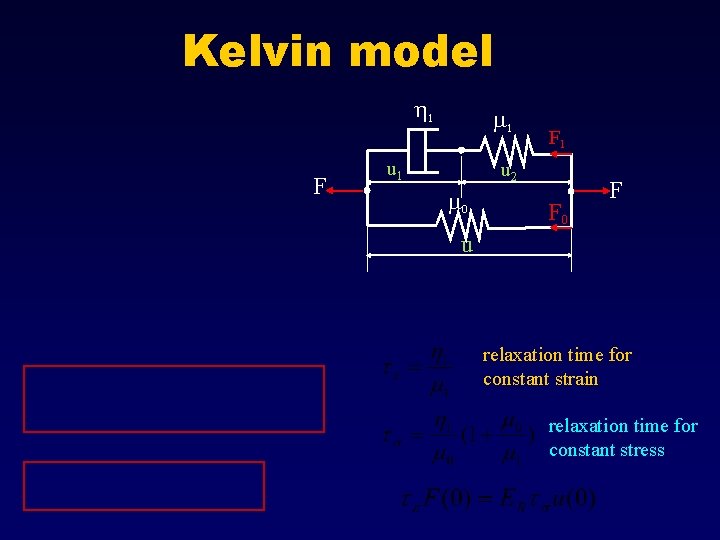
Kelvin model h 1 F m 1 u 1 F 1 u 2 m 0 F u relaxation time for constant strain relaxation time for constant stress

Creep function When F(t) is unit-step function, solutions of (1)(2)(3) unit-step function

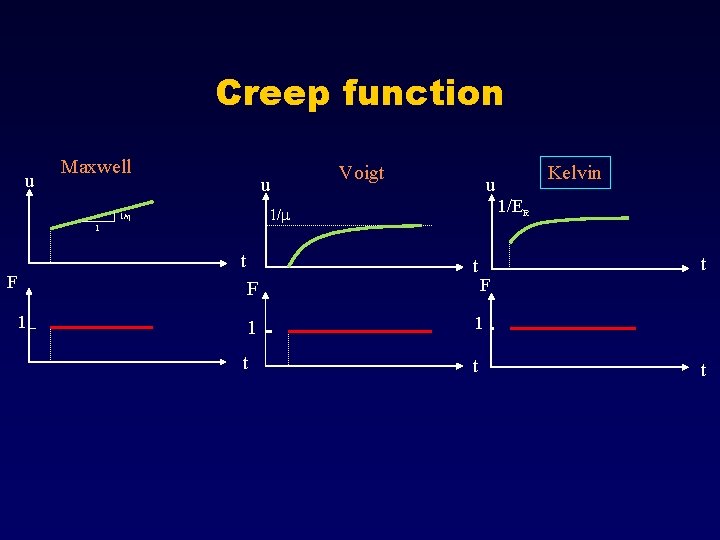
Creep function u Maxwell u 1 t 1 Kelvin u 1/ER 1/m 1/h F Voigt t t F F 1 1 t t t

Relaxation function When u(t) is a unit-step function, F(t)=k(t) d 1

Relaxation function m Maxwell F m Kelvin F hd(t-t 0) Voigt ER u u u 1 1 1 t 0 t

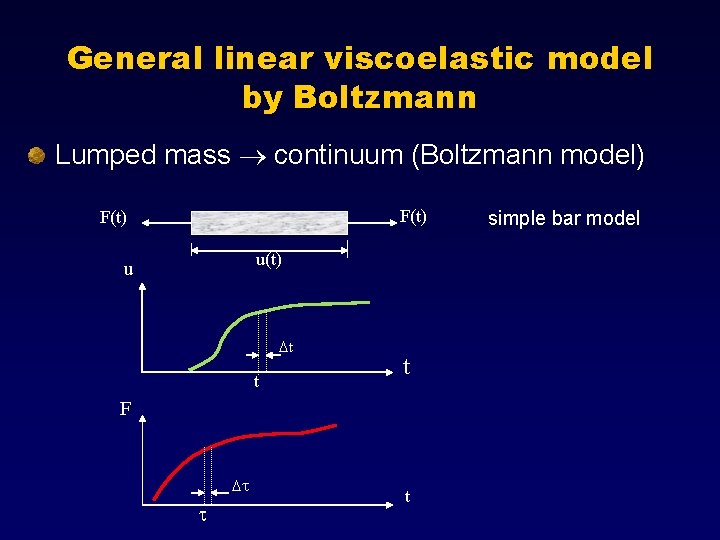
General linear viscoelastic model by Boltzmann Lumped mass continuum (Boltzmann model) F(t) u(t) u Dt t t F Dt t t simple bar model

Assumptions F(t) continuous & differentiable In dt, increment of F(t) = (d. F/dt)dt Increment of u(t) due to F(t): du(t), t > t Relationship between du(t) and F’(t)dt creep function convolution integral

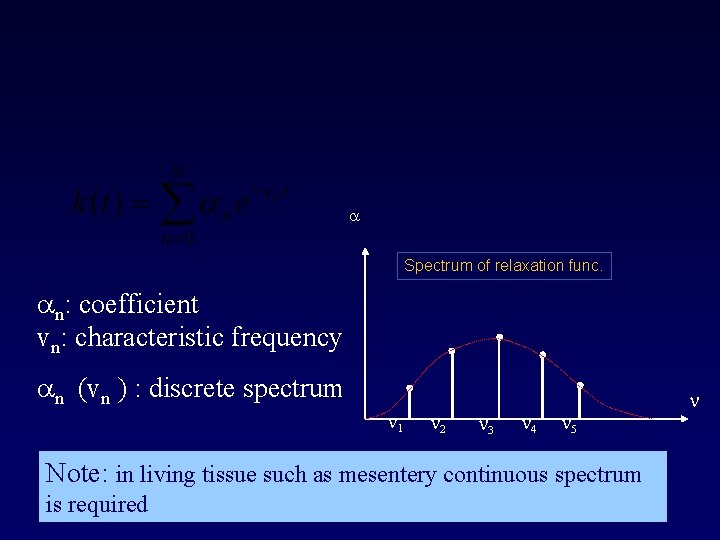
Similarly, we can define the relaxation function Notes: 1) Maxwell, Voigt & Kelvin models are special case of Boltzmann model 2) Relaxation function can be approximated by Fourier series

a Spectrum of relaxation func. an: coefficient vn: characteristic frequency an (vn ) : discrete spectrum n 1 n 2 n 3 n 4 n 5 Note: in living tissue such as mesentery continuous spectrum is required n

Generalization to viscoelastic materials Assumptions: small deformation, infinitesimal displacements, strains and velocities F , u e, c, k tensor

Initial condition Assume ij=eij=0, t<0 Note: the 1 st term is due to the initial disturbance (condition)

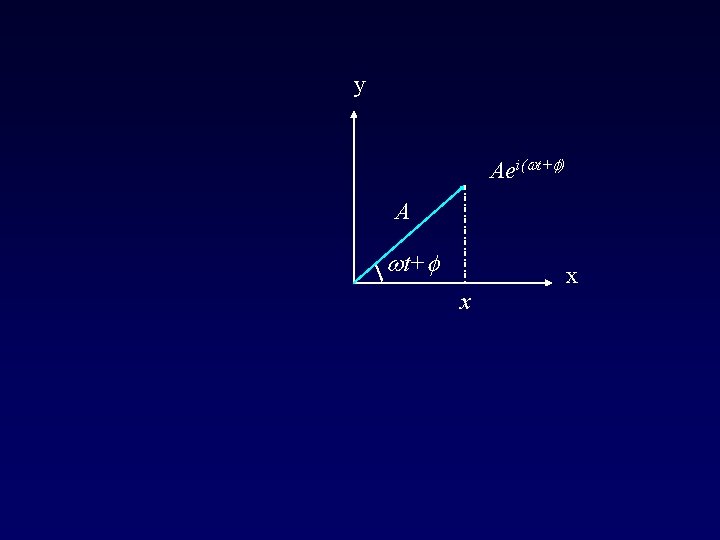
2. 12 Response of a viscoelastic body to harmonic excitation Most biological tissues ~ viscoelastic, periodic oscillation is a simple method Simple harmonic motion: x A: amplitude, f: phase angle x = projection of a rotating vector (phasor) on real axis

y Aei(wt+f) A wt+f x x

Response of Maxwell body to harmonic excitation Maxwell material

Maxwell material Substitute into above equation

Maxwell material

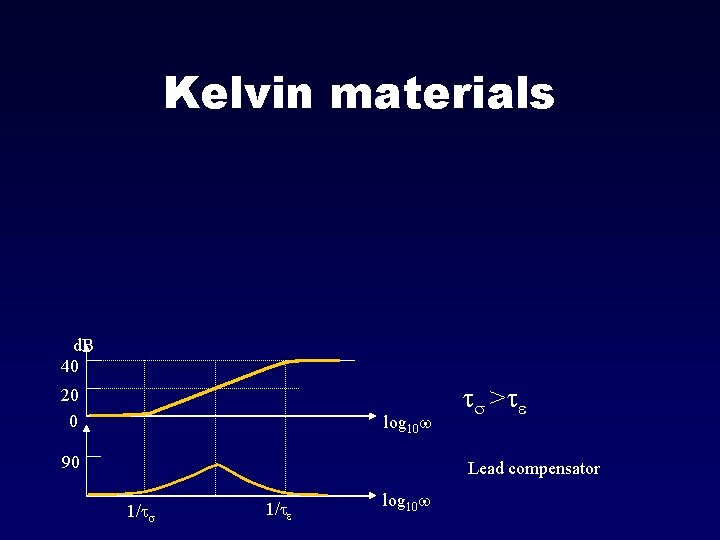
Kelvin materials

Kelvin materials d. B 40 20 0 log 10 w 90 t >te Lead compensator 1/te log 10 w

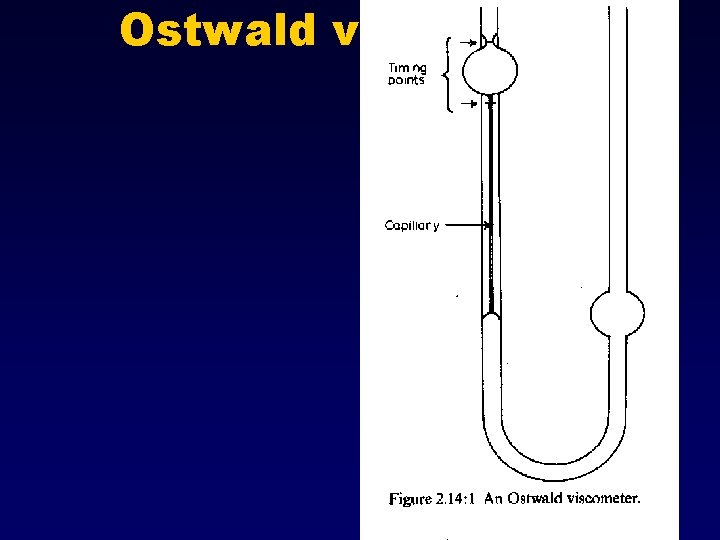
2. 14 Methods of Testing Different aspects of biological materials l Lack large samples of biological materials l Keep samples viable & close to in vivo condition l nonhomogeneous Viscometry (biofluids) l Ostwald viscometer l Couette viscometer l Cone-plate viscometer l Weissenberg’s rheogoniometer (general instrument) l Other types

Ostwald viscometer

Ostwald viscometer For Newtonian fluid in a laminar flow Unit: dyn. s/cm 2 or poise, (CGS) N. s/m 2 (MKS) 1 poise = 0. 1 N. s/m 2

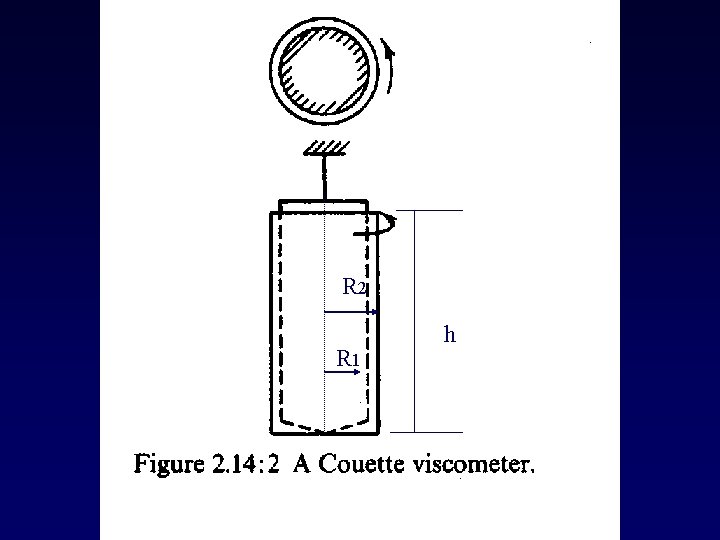
Couette Viscometer R 2 R 1 h

Couette Viscometer Flow between two coaxial cylinders Rotating outer cylinder (R 2), angular velocity w, inner cylinder (R 1) torque M, height of liquid h

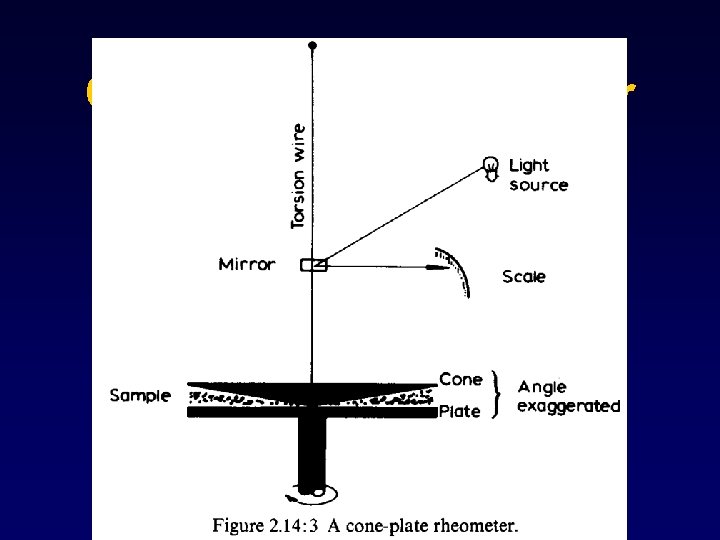
Cone-plate Viscometer

Cone-plate Viscometer Higher accuracy, cone gap yield constant shear rate operated in steady rotation or oscillatory or step change modes Complex modulus of viscoelastic materials

Weissenberg’s rheogoniometerr Weissenberg’s effect – uptrust or normal force occurs in some non. Newtonian fluids; in Couette flow the fluid will climb up inner cylinder Measure force at all angles

Others Vertical rod oscillated sinusoidally within a hollow cylinder containing the material Placed between a spherical bob and a concentric hemisphere cup Tuning fork to drive an oscillatory rod in fluid either in axial or lateral motion Falling or rising small sphere, a metal or plastic sphere falls or rises through a known distance and measure the time. For Newtonian flow, Reynold no. <<1

Biosolids Material testing machines Specimen is clamped and stretched or shortened at a specific rate while both the force and displacement are recorded. For biological materials, small size & need to keeping specimen viable!

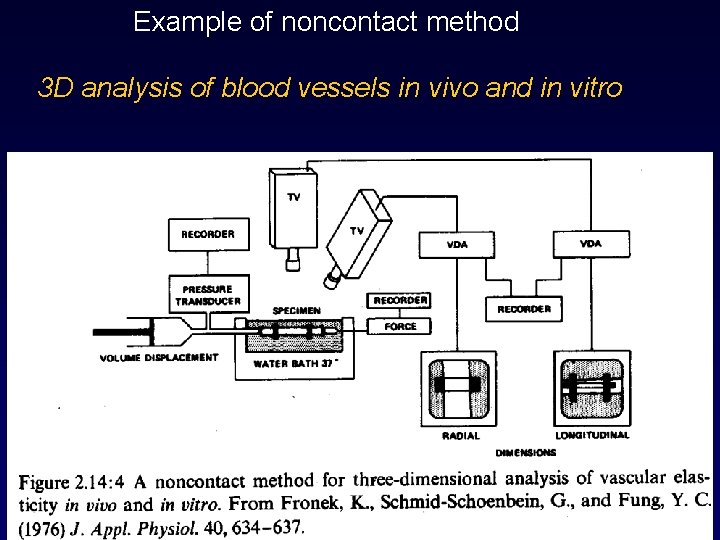
Example of noncontact method 3 D analysis of blood vessels in vivo and in vitro

2. 15 Mathematical Development of Constitutive Equations Nonviscous ideal fluid, Newtonian viscous fluid, Hookean elastic solid, linear viscoelastic (Maxwell, Voigt, Kelvin), Boltzmann Finite deformation, nonlinear between strain and deformation gradients: Cauchy, Green, St. Venant, Almansi & Hamel -> nonlinear constitutive equations for elastic, viscoplastic materials [Rivlin, Trusdell 50 s 60 s]

Nonlinear viscoelastic material, Green & Rivlin (’ 57) & Green, Rivlin & Spencer (’ 59), multiple integral constitutive equation, series solutions. Non-Newtonian fluid mechanics developed for polymer plastics industry (Bird et. al. ’ 77) Constitutive laws of most biological tissues were not known, can not formulate boundaryvalue problems, nor analysis, prediction. To give an account of mechanical properties of living tissues, consolidated in constitutive equations