Ch 2 Quarter TEST Review RELATION A correspondence















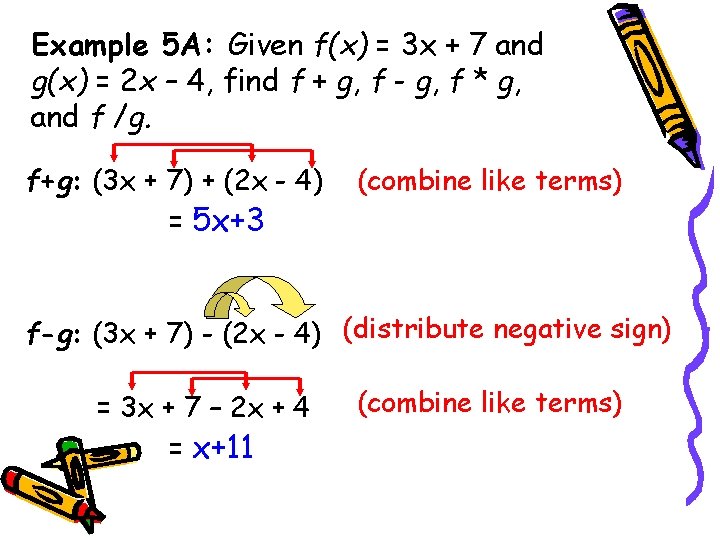














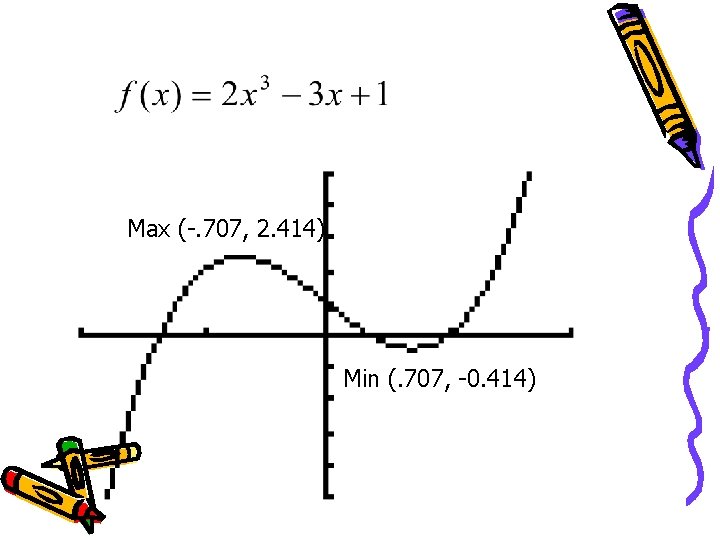

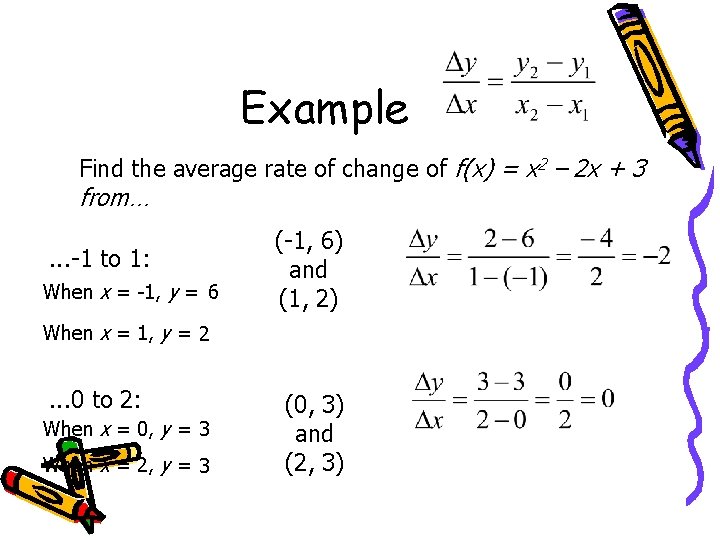











- Slides: 78

Ch 2 Quarter TEST Review

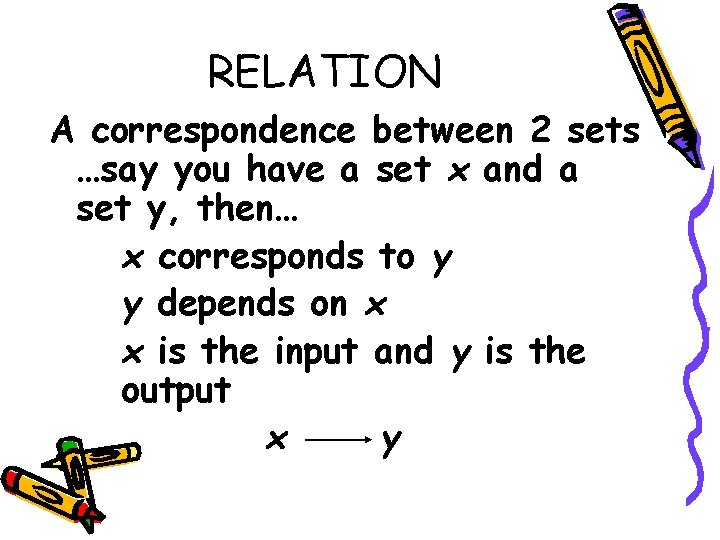
RELATION A correspondence between 2 sets …say you have a set x and a set y, then… x corresponds to y y depends on x x is the input and y is the output x y

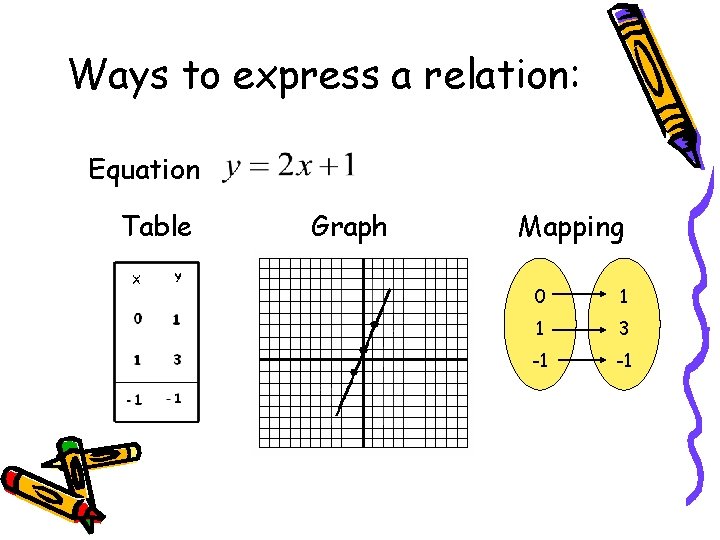
Ways to express a relation: Equation Table Graph Mapping 0 1 1 3 -1 -1

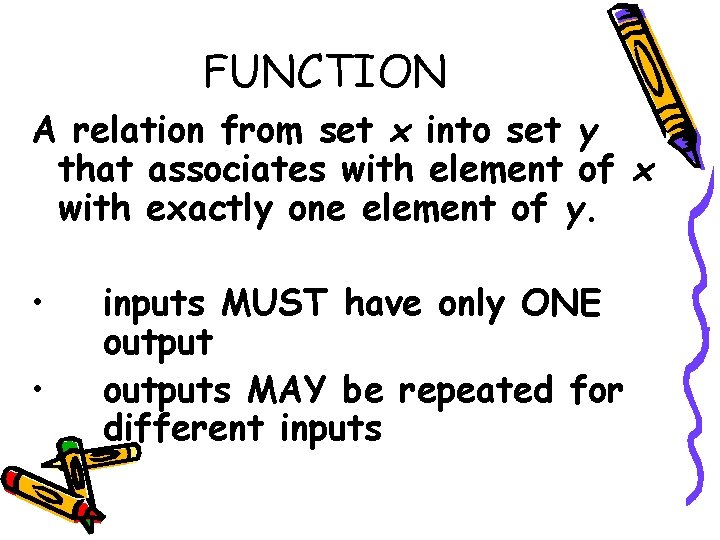
FUNCTION A relation from set x into set y that associates with element of x with exactly one element of y. • • inputs MUST have only ONE outputs MAY be repeated for different inputs

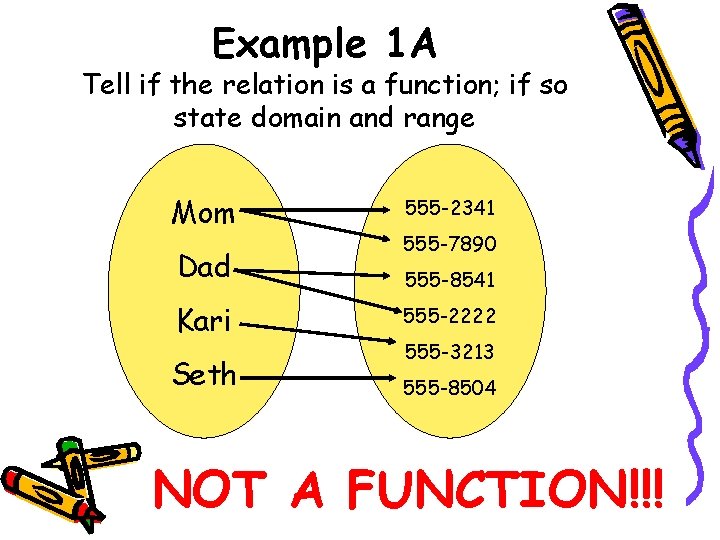
Example 1 A Tell if the relation is a function; if so state domain and range Mom Dad Kari Seth 555 -2341 555 -7890 555 -8541 555 -2222 555 -3213 555 -8504 NOT A FUNCTION!!!

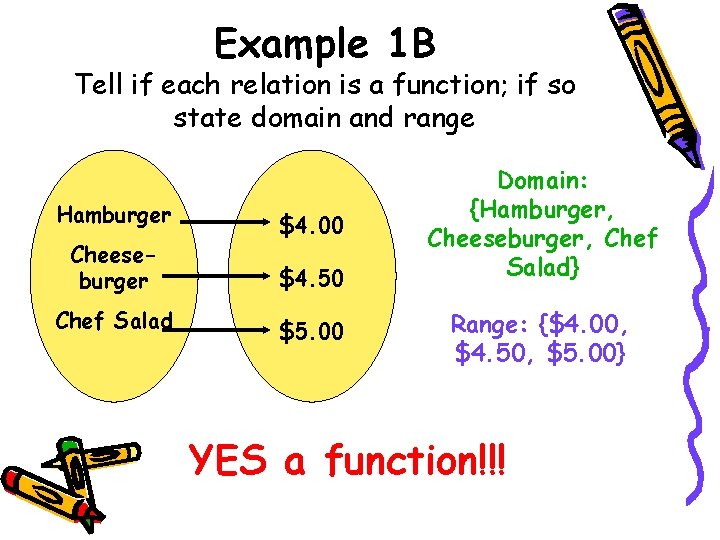
Example 1 B Tell if each relation is a function; if so state domain and range Hamburger Cheeseburger Chef Salad $4. 00 $4. 50 $5. 00 Domain: {Hamburger, Cheeseburger, Chef Salad} Range: {$4. 00, $4. 50, $5. 00} YES a function!!!

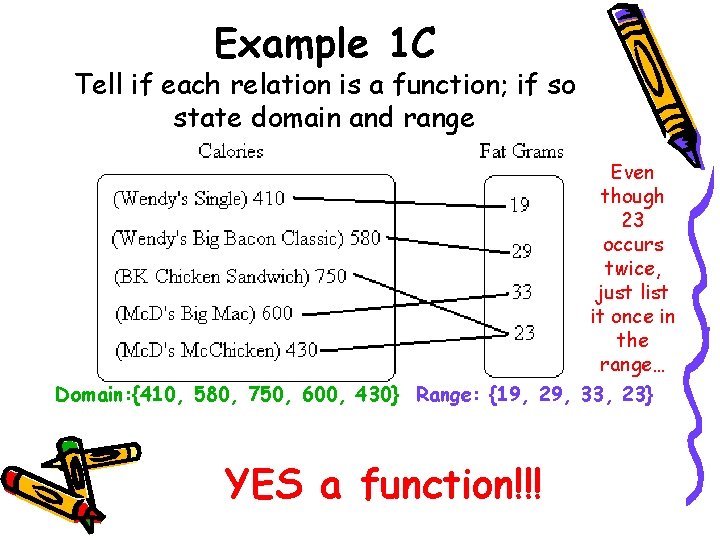
Example 1 C Tell if each relation is a function; if so state domain and range Even though 23 occurs twice, just list it once in the range… Domain: {410, 580, 750, 600, 430} Range: {19, 29, 33, 23} YES a function!!!

Example 1 D Tell if each relation is a function; if so state domain and range {(1, 4), (3, 5), (5, 7), (7, 9)} YES a function!! Domain: {1, 3, 5, 7} Range: {4, 5, 7, 9}

Example 1 E Tell if each relation is a function; if so state domain and range {(4, -2), (1, -1), (0, 0), (1, 1), (4, 2)} NOT a function!! Because the 4 and 1 in the domain each have more than one output!

Example 1 F Tell if each relation is a function; if so state domain and range {(-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)} YES a function!! Outputs CAN be repeated…just not elements of the domain! Domain: {-2, -1, 0, 1, 2} Range: {4, 1, 0}

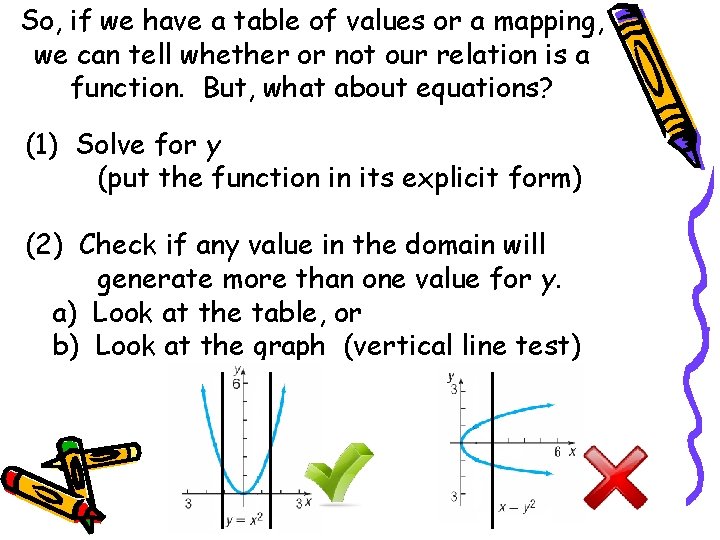
So, if we have a table of values or a mapping, we can tell whether or not our relation is a function. But, what about equations? (1) Solve for y (put the function in its explicit form) (2) Check if any value in the domain will generate more than one value for y. a) Look at the table, or b) Look at the graph (vertical line test)

Example 2 Determine whether the equation defines y as a function of x. Example B Example A +3 x Step 1: solve for y by adding 3 x to each side… -x 2 Step 1: solve for y by subtracting x 2 from both sides… Take the square root: Step 2: graph on calculator/look at table… Step 2: graph the two equations on calculator…

Finding Values of a Function • f(x) means “the value of f at the number x” • The independent variable is called the argument x is the input and f(x) is the output or value…

Example 3: Evaluate the following for the function, f, defined by Just plug it in & simplify! A. f(3) = 3(3)2 + 5(3) =42 B. f(x) + f(3) = f(x) + 42 Remember: f(3) = 42… …and f(x) is 3 x 2 + 5 x = 3 x 2 + 5 x + 42

Example 3 cont… C. f(-x) = 3(-x)2 + 5(-x) = 3 x 2 + 5(-x)2 =x 2 5(-x) = -5 x = 3 x 2 - 5 x D. - f(x) This means the opposite of f(x)… = - (3 x 2 + 5 x) …distribute the negative… = - (3 x 2 + 5 x) = -3 x 2 – 5 x

Example 3 cont… E. f(x + 3) = 3(x + 3)2 + 5(x + 3) 2 = (x + 3) = x 2 +6 x + 9 = 3(x 2 + 6 x + 9) + 5(x + 3) distribute the 3 and 5… = 3 x 2 + 18 x + 27 + 5 x + 15 …combine like terms = 3 x 2 + 23 x + 42

Example 3 cont… F. 1 st take care of f(x + h) = 3(x + h) 2 + 5(x + h) = 3(x 2 + 2 xh + h 2) + 5(x + h) distribute the 3 and 5… = 3 x 2 + 6 xh + 3 h 2 + 5 x + 5 h f(x + h) = 3 x 2 + 6 xh + 3 h 2 + 5 x + 5 h

Example 3 F cont… f(x + h) – f(x) = = 3 x 2 + 6 xh + 3 h 2 + 5 x + 5 h - (3 x 2 + 5 x) distribute the negative… = 3 x 2 + 6 xh + 3 h 2 + 5 x + 5 h - 3 x 2 - 5 x …combine like terms… …and factor. = 6 xh + 3 h 2 + 5 h = h (6 x + 3 h + 5) = 6 x + 3 h + 5

The Domain of a Function If an equation for a function, f, is given with no specified domain, it is agreed that the domain of f is the largest set of real numbers for which the value of f(x) is a real number. In other words: The domain is all inputs that make sense and give an answer for the equation…

Example 4: Find the domain of each function. What can x NOT be? ? Verify with a graph! A. all real numbers ny a e b an c x ! g n i th o B. er z a e ! v a m h o t t t o o n b Can the on x is undefined at -1 and 1

Example 4 continued: Find the domain of each function. the ke a t f o ann root o er! c b m You uare u sq tive n a neg C. +5 t …add 5 t to both sides… …divide both sides by 5… or

Operations on Functions can be added, subtracted, multiplied and divided: If f and g are functions, then. . .
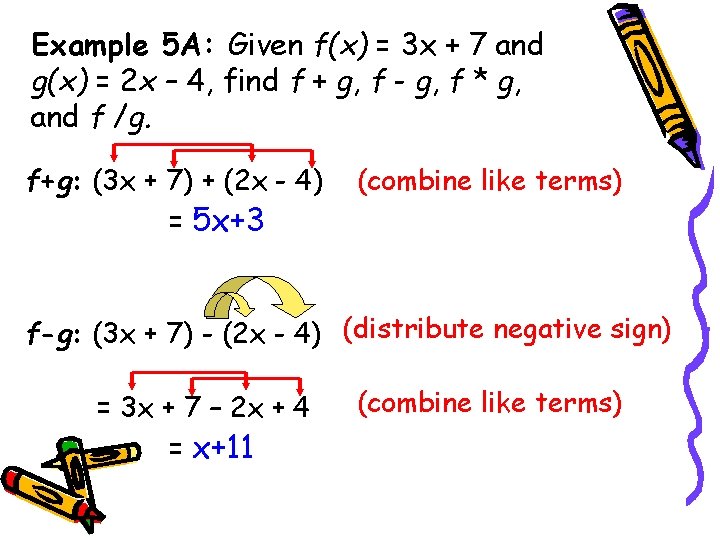
Example 5 A: Given f(x) = 3 x + 7 and g(x) = 2 x – 4, find f + g, f - g, f * g, and f /g. f+g: (3 x + 7) + (2 x - 4) = 5 x+3 (combine like terms) f-g: (3 x + 7) - (2 x - 4) (distribute negative sign) = 3 x + 7 – 2 x + 4 = x+11 (combine like terms)

Example 5 A continued: Given f(x) = 3 x + 7 and g(x) = 2 x – 4 f *g: (3 x + 7)(2 x - 4) (FOIL. . . multiply) = 6 x 2 – 12 x + 14 x – 28 (simplify) = 6 x 2 + 2 x - 28 f/g: (3 x + 7)/(2 x – 4) (There is nothing more to do!) = 3 x + 7 2 x - 4

Example 5 B: Given f(x) = 3/x and g(x) = 1/x, find f + g, f - g, f * g, and f /g. f+g: f-g: (must have a common denominator whenever adding or subtracting fractions)

Example 5 B continued: Given f(x) = 3/x and g(x) = 1/x f *g: (top x top bottom x bottom) f/g: (flip and multiply!)

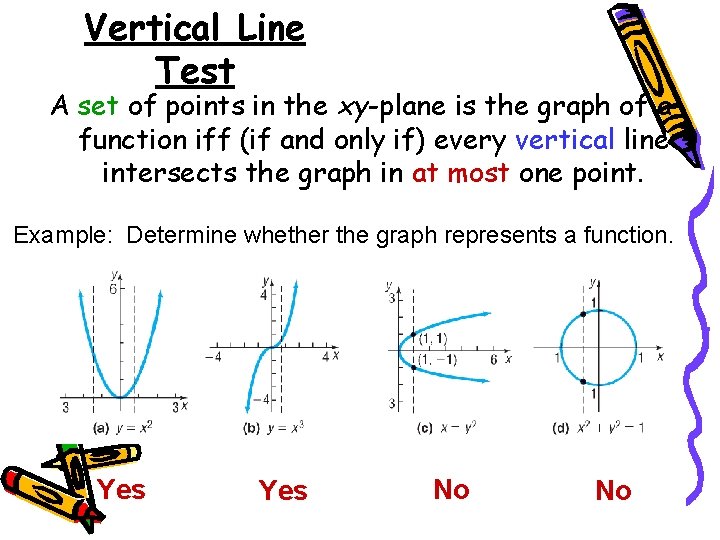
Vertical Line Test A set of points in the xy-plane is the graph of a function iff (if and only if) every vertical line intersects the graph in at most one point. Example: Determine whether the graph represents a function. Yes No No

Many things can be learned about a function from its graph, such as (but certainly not limited to) values of the function (f(x)) at various values of x, the domain and range, the intercepts (both x and y), the number of times a function is intersected by other functions, and values of x that generate different function values.

EXAMPLE (a) Is the point (1, ½) on the graph of f? (use table on calc. ) yes (b) If x = 2, what is f(x)? What point is on the graph of f? f(x)=⅔ (2, ⅔) (c) If f(x) = 2, what is x? What point is on the graph of f? x = -2 (-2, 2) (e) (d) Find any x-intercepts. (0, 0) (a) Find any y-intercepts. (0, 0)

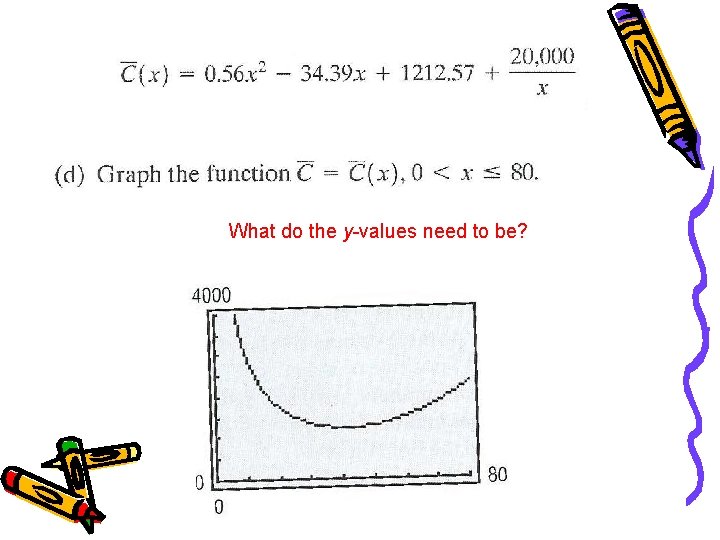
EXAMPLE The average cost C of manufacturing x computers per day is given by the function Determine the average cost of manufacturing: (a) 30 computers in a day $1351. 54 (b) 40 computers in a day $1232. 97 (c) 50 computers in a day $1293. 07

What do the y-values need to be?

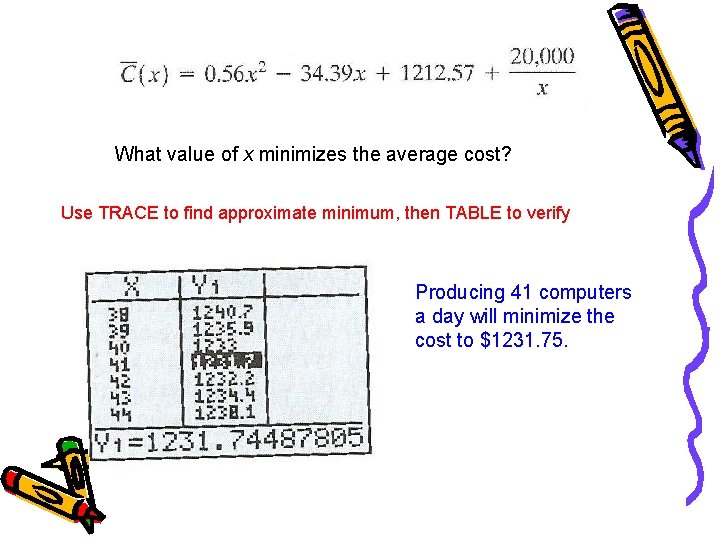
What value of x minimizes the average cost? Use TRACE to find approximate minimum, then TABLE to verify Producing 41 computers a day will minimize the cost to $1231. 75.

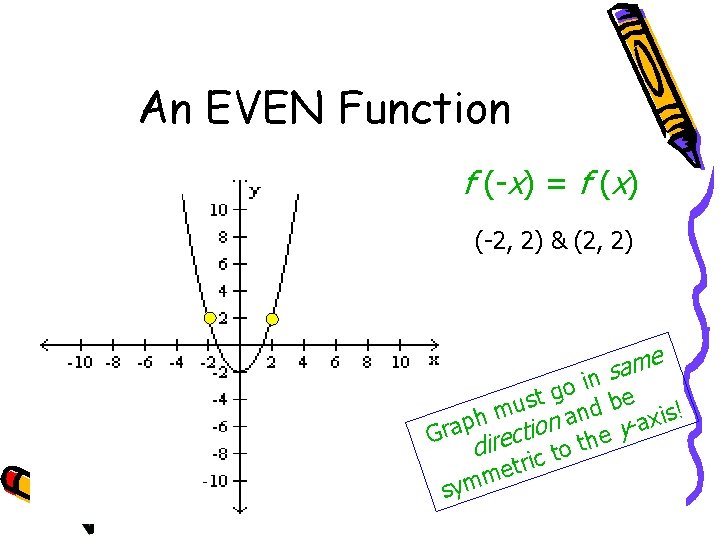
Determining Even and Odd Functions from the Graph A function, f, is even if for every number x in its domain the number –x is also in the domain and f(-x) = f(x). . . that is, if (x, y) is on the graph, then (-x, y) is too. Also, a function is even iff its graph is symmetric with respect to the y-axis. f (-x) = f (x)

An EVEN Function f (-x) = f (x) (-2, 2) & (2, 2) e m a in s go be t s u d ! m s n i a h x p a Gra irection the yd o t c i etr m sym

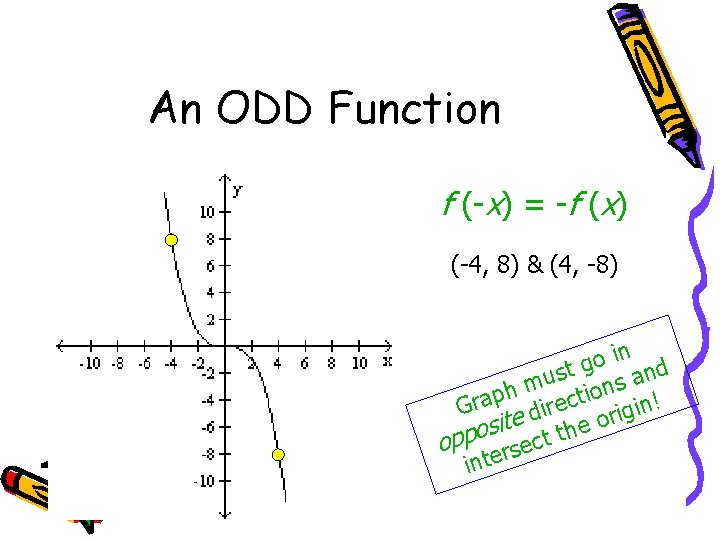
Determining Even and Odd Functions from the Graph A function, f, is odd if for every number x in its domain the number –x is also in the domain and f(-x) = f(x). . . that is, if (x, y) is on the graph, then (-x, -y) is too. Also, a function is odd iff its graph is symmetric with respect to the origin. f (-x) = -f (x)

An ODD Function f (-x) = -f (x) (-4, 8) & (4, -8) in o g d t s n a u m ns h o i p t a rec rigin! Gr i d te the o i s o opp ersect int

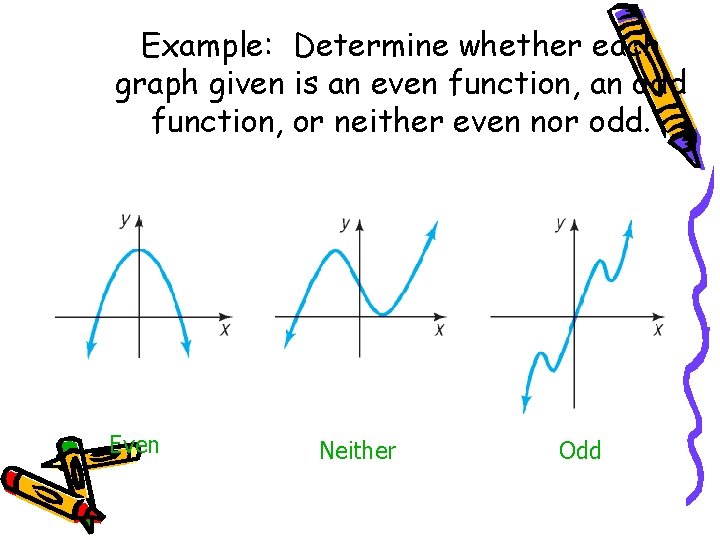
Example: Determine whether each graph given is an even function, an odd function, or neither even nor odd. Even Neither Odd

Identifying Even and Odd Functions Algebraically EXAMPLE Determine whether each function is even or odd. . . verify algebraically. A. Graph it…does it appear to be even or odd? To verify algebraically, you must prove that f(-x) = f(x) Since f(-x) = f(x), then it’s an EVEN function!

Identifying Even and Odd Functions Algebraically Graph it…does it appear to be even or odd? B. To verify algebraically, first prove that Therefore it is not even… So now prove that Not odd… Then it’s NEITHER even nor odd!

Identifying Even and Odd Functions Algebraically Graph it…does it appear to be even or odd? C. First find f(-x). . . Then find -f(x). . . Since f(-x) = -f(x), then it’s an ODD function!

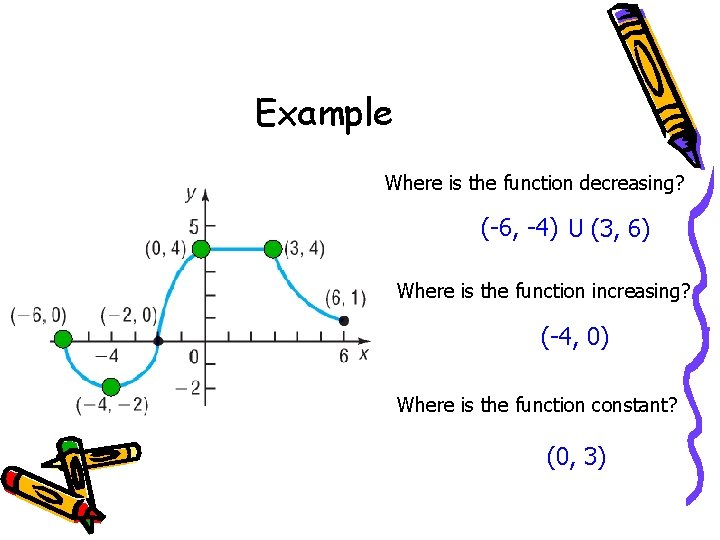
Determining Where a Function is Increasing, Decreasing, or Constant Look from left to right along a graph and find the parts of the graph that are rising (increasing), falling (decreasing), and horizontal (constant). REMEMBER: these are INTERVALS named by the x coordinates!

Example Where is the function decreasing? (-6, -4) U (3, 6) Where is the function increasing? (-4, 0) Where is the function constant? (0, 3)

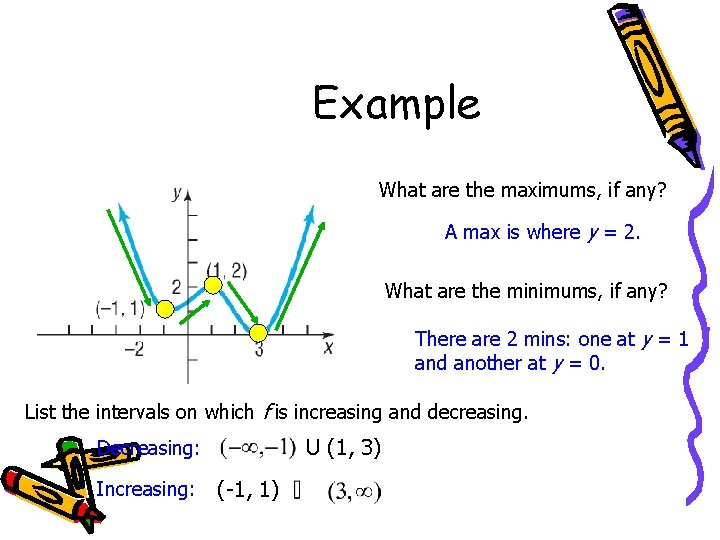
Finding Local Maximums and Local Minimums Maximums are the hills and minimums are the valleys. . . REMEMBER: these are named by the y coordinates! On your calculator: TRACE to the point, then 2 nd – calc – (3) minimum or (4) maximum

Example What are the maximums, if any? A max is where y = 2. What are the minimums, if any? There are 2 mins: one at y = 1 and another at y = 0. List the intervals on which f is increasing and decreasing. U (1, 3) Decreasing: Increasing: (-1, 1)

Example Use the graphing calculator to graph the function for. Find local maximums and minimums and determine the intervals of increase and decrease. NOTE: Always sketch your graph and fill in the points!
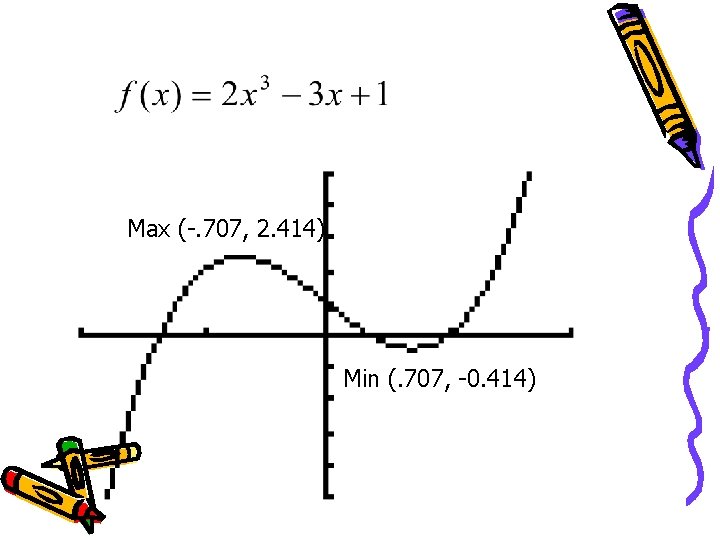
Max (-. 707, 2. 414) Min (. 707, -0. 414)

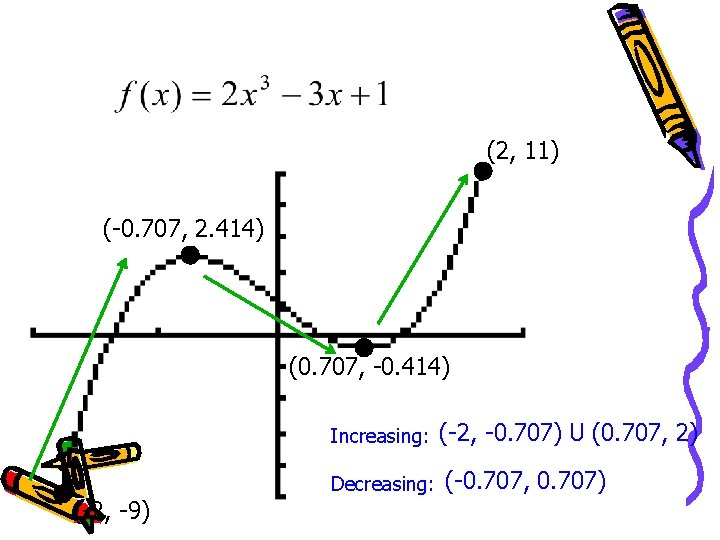
(2, 11) (-0. 707, 2. 414) (0. 707, -0. 414) (-2, -9) Increasing: (-2, -0. 707) U (0. 707, 2) Decreasing: (-0. 707, 0. 707)

Average Rate of Change of a Function If c is in the domain of a function, f, the average rate of change of f from c to x is defined: , where This is just calculating the slope between two points!! (In calculus, this expression is called the difference quotient of f at c. )
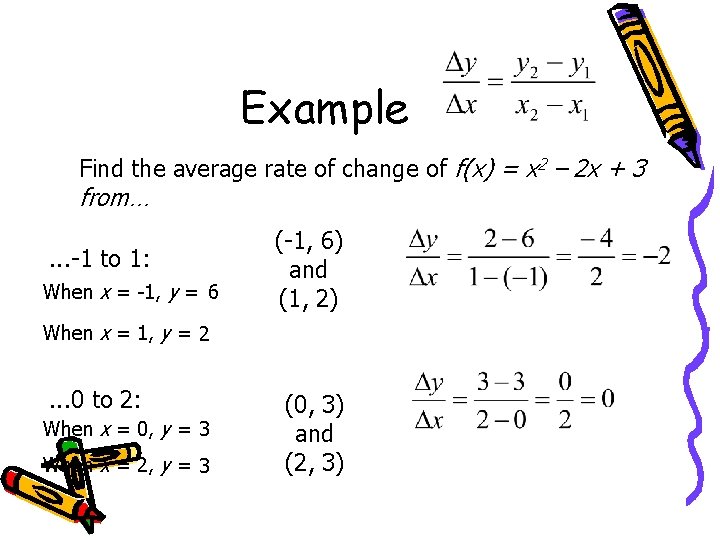
Example Find the average rate of change of f(x) = x 2 – 2 x + 3 from… . . . -1 to 1: When x = -1, y = 6 (-1, 6) and (1, 2) When x = 1, y = 2 . . . 0 to 2: When x = 0, y = 3 When x = 2, y = 3 (0, 3) and (2, 3)

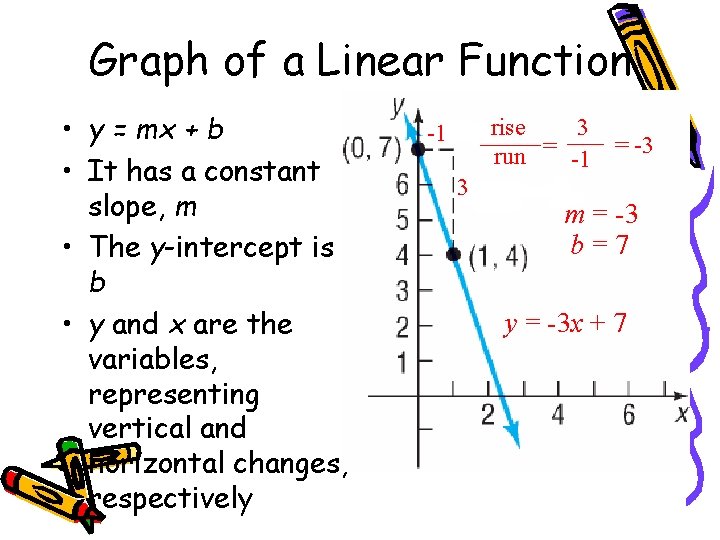
Graph of a Linear Function • y = mx + b • It has a constant slope, m • The y-intercept is b • y and x are the variables, representing vertical and horizontal changes, respectively 3 rise run = -1 = -3 -1 3 m = -3 b=7 y = -3 x + 7

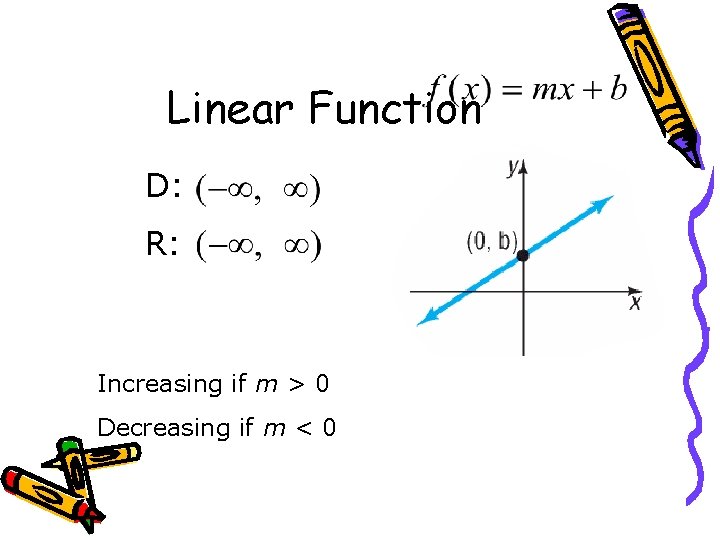
Linear Function D: R: Increasing if m > 0 Decreasing if m < 0

Constant Function D: R: b m=0 A special linear function. . . an even function.

Identity Function D: R: m=1 b=0 A special linear function where x = y An odd function Increasing from

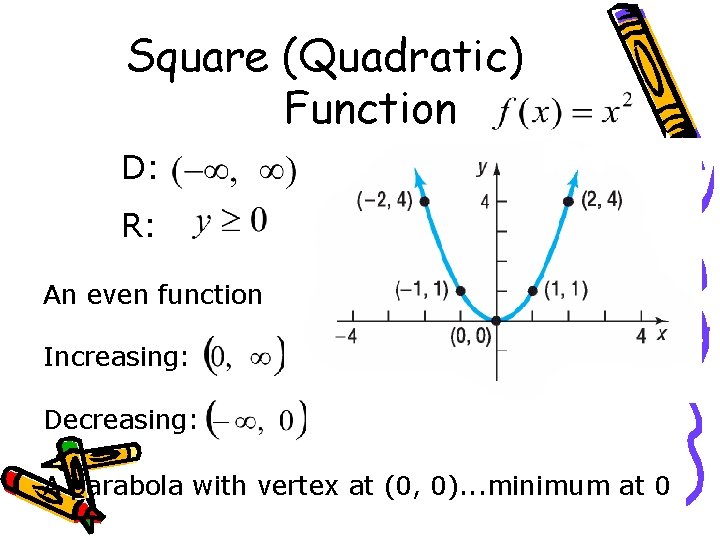
Square (Quadratic) Function D: R: An even function Increasing: Decreasing: A parabola with vertex at (0, 0). . . minimum at 0

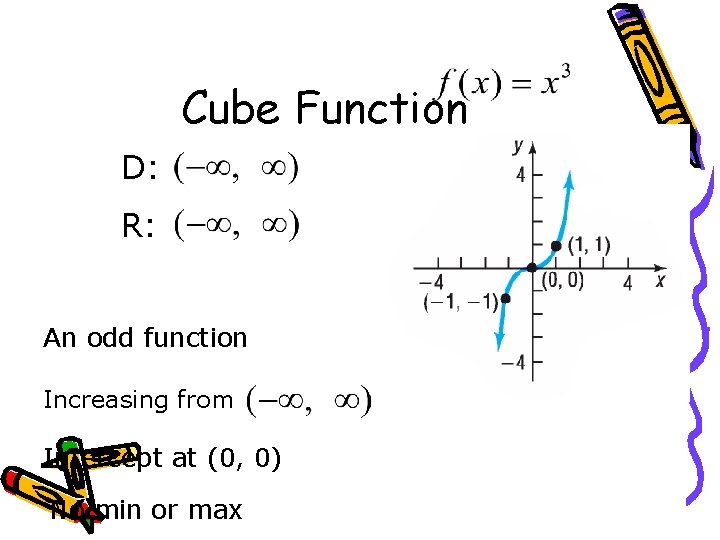
Cube Function D: R: An odd function Increasing from Intercept at (0, 0) No min or max

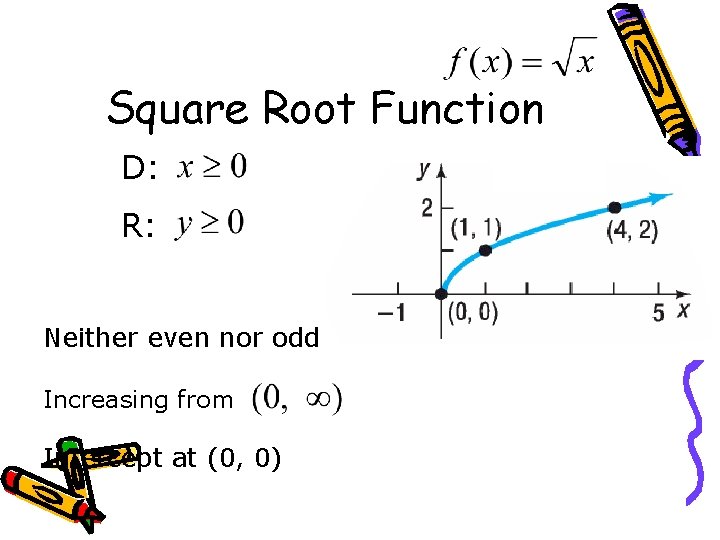
Square Root Function D: R: Neither even nor odd Increasing from Intercept at (0, 0)

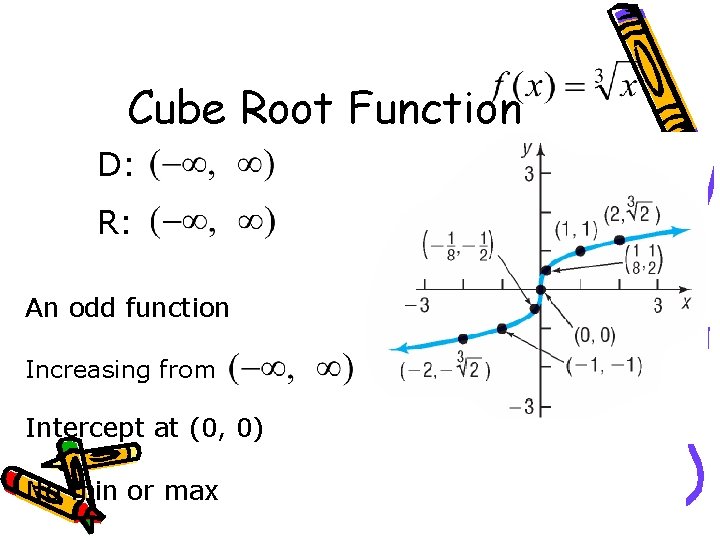
Cube Root Function D: R: An odd function Increasing from Intercept at (0, 0) No min or max

Reciprocal (Inverse) Function D: R: Has a vertical and horizontal asymptote An odd function No intercepts No min or max Decreasing from Is discontinuous

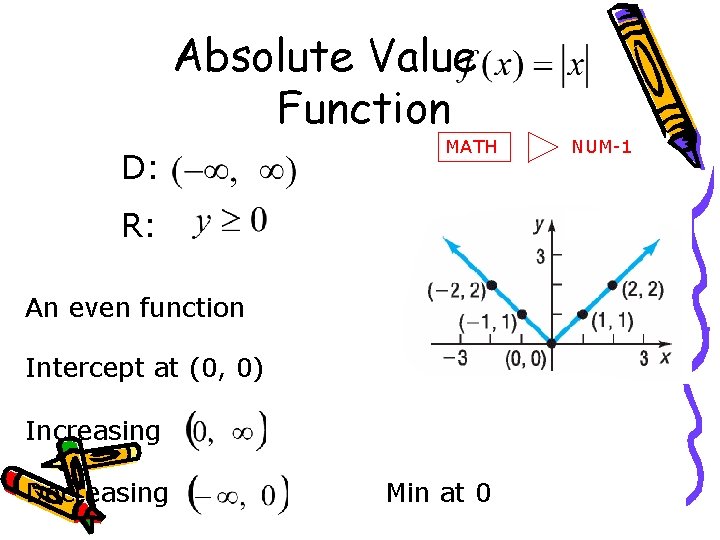
Absolute Value Function D: MATH R: An even function Intercept at (0, 0) Increasing Decreasing Min at 0 NUM-1

Greatest Integer (Step) Function The largest integer less than or equal to x. D: R: integers Neither even nor odd x-intercept at [0, 1) discontinuous MATH NUM-5

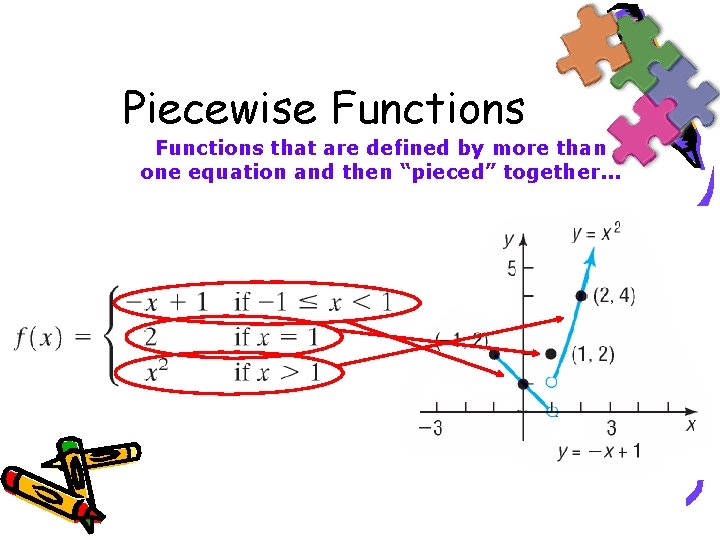
Piecewise Functions that are defined by more than one equation and then “pieced” together. . .

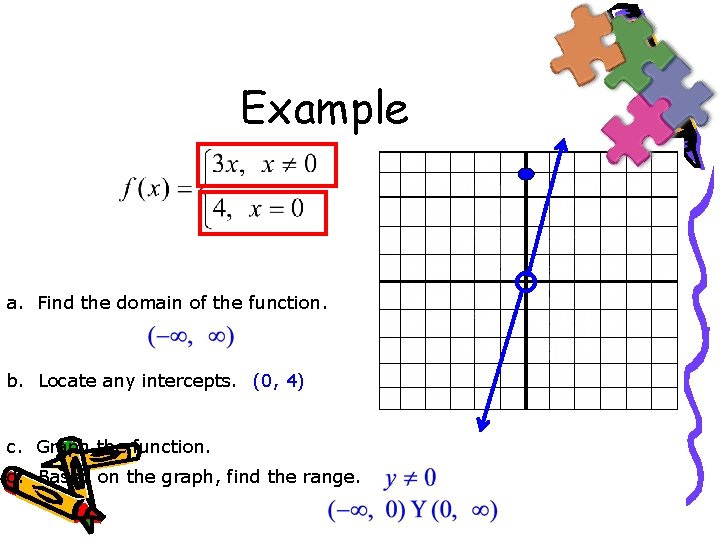
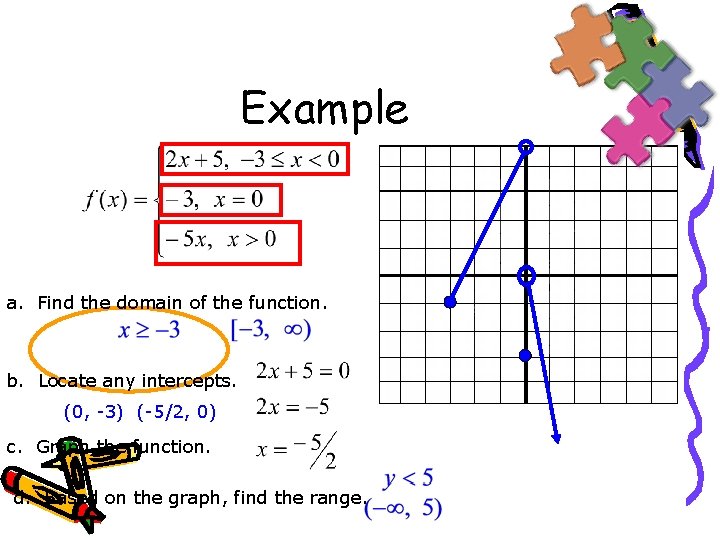
Example a. Find the domain of the function. b. Locate any intercepts. (0, 4) c. Graph the function. d. Based on the graph, find the range.

Example a. Find the domain of the function. b. Locate any intercepts. (0, -3) (-5/2, 0) c. Graph the function. d. Based on the graph, find the range.

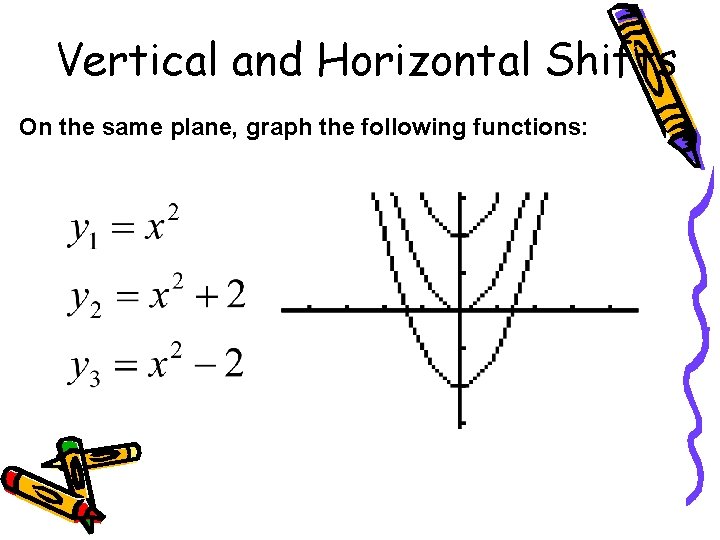
Vertical and Horizontal Shifts On the same plane, graph the following functions:

up 2 (x, y + 2) down 2 (x, y - 2) Conclusion: A vertical shift occurs whenever a number is added or subtracted to the whole function. It shifts up if a number is added; it shifts down if a number is subtracted. y = f(x) + k y = f(x) - k

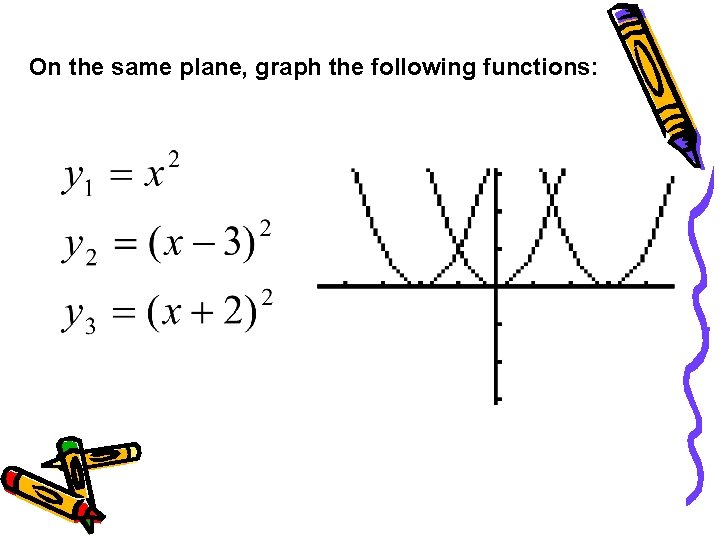
On the same plane, graph the following functions:

right 3 left 2 (x + 3, y) (x - 2, y) NOTE: Always the OPPOSITE effect with x’s!!! Conclusion: A horizontal shift occurs whenever a number is added or subtracted from the x part of a function. It shifts left if a number is added; it shifts right if a number is subtracted. y = f(x + h) y = f(x – h)

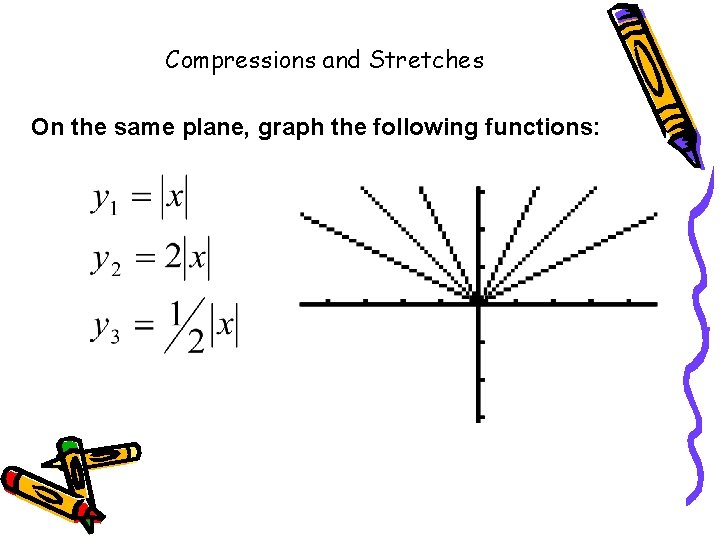
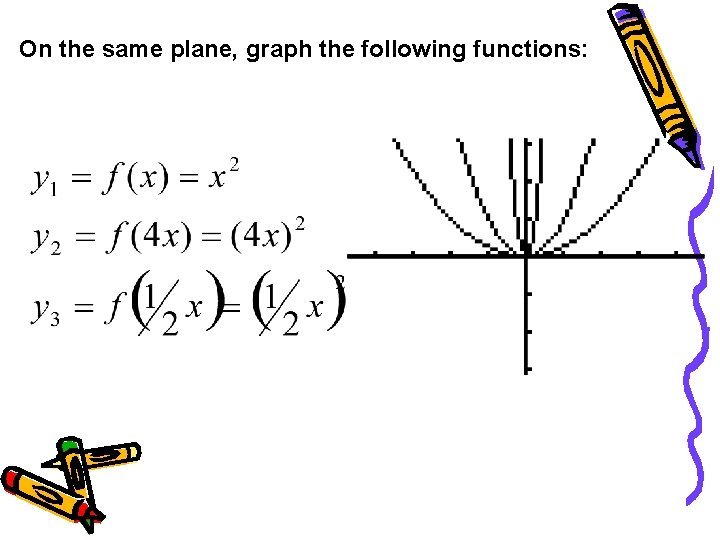
Compressions and Stretches On the same plane, graph the following functions:

narrower wider (x, 2 y) (x, ½y) vertical stretch by factor 2 vertical compression by factor ½ Conclusion: A vertical stretch/compression occurs whenever the whole function is multiplied by a number. A vertical stretch occurs if the number is greater than 1; a vertical shrink occurs if the number is 0<n<1. y = af(x)

On the same plane, graph the following functions:

narrower wider (1/4 x, y) horizontal compression by factor 1/4 horizontal (2 x, y) stretch by factor 2 NOTE: Always the OPPOSITE effect with x’s!!! Multiply by the RECIPROCAL! A horizontal compression is like a vertical stretch and a horizontal stretch is like a vertical compression. . .

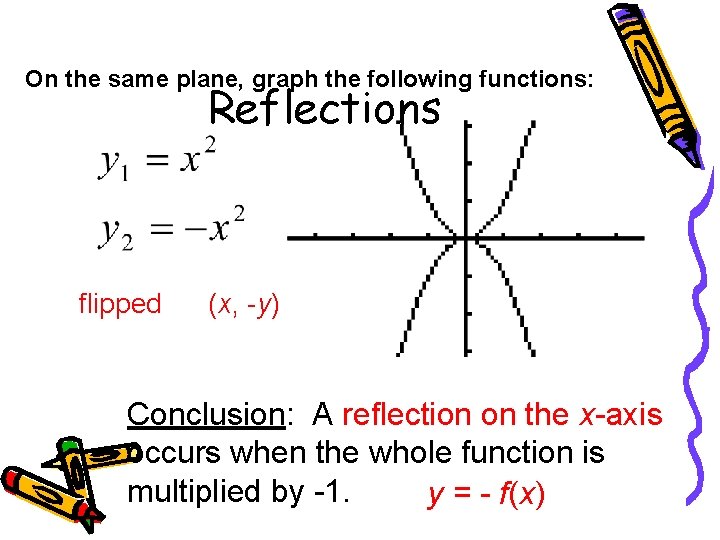
On the same plane, graph the following functions: Reflections flipped (x, -y) Conclusion: A reflection on the x-axis occurs when the whole function is multiplied by -1. y = - f(x)

On the same plane, graph the following functions: flipped (-x, y) Conclusion: A reflection on the y-axis occurs when the x part of a function is multiplied by -1. y = f(- x)

Summary of Graphing Techniques (x, y + k) (x, y - k) (x + h, y) (x - h, y) (x, ay) (1/ax, y) (x, -y) (-x, y)

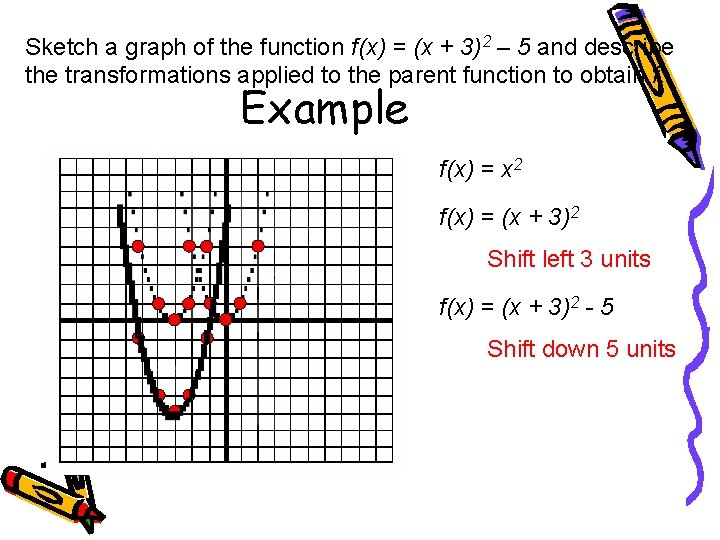
Sketch a graph of the function f(x) = (x + 3)2 – 5 and describe the transformations applied to the parent function to obtain f. Example f(x) = x 2 f(x) = (x + 3)2 Shift left 3 units f(x) = (x + 3)2 - 5 Shift down 5 units

Example Find the function that is graphed after the following transformations are applied to f(x) = |x|. . . (-1, 1) (0, 0) (1, 1) 1) shift left 2 units |x + 2| (-3, 1) (-2, 0) (-1, 1) 2) shift up 3 units |x + 2| + 3 (-3, 4) (-2, 3) (-1, 4) subtract 2 from x add 3 to y 3) reflect on y-axis |-x + 2| + 3 (3, 4) (2, 3) (1, 4) opposite of x Check ordered pairs. . . (-x + 2, y + 3) f(x) = |-x + 2| + 3

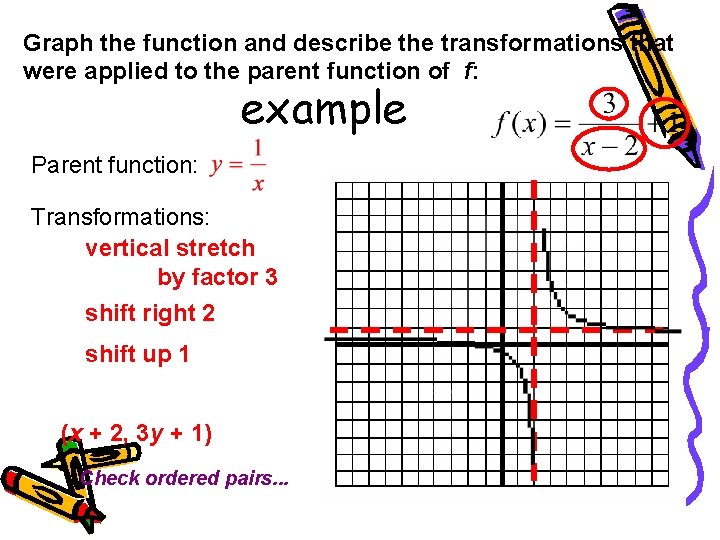
Graph the function and describe the transformations that were applied to the parent function of f: example Parent function: Transformations: vertical stretch by factor 3 shift right 2 shift up 1 (x + 2, 3 y + 1) Check ordered pairs. . .

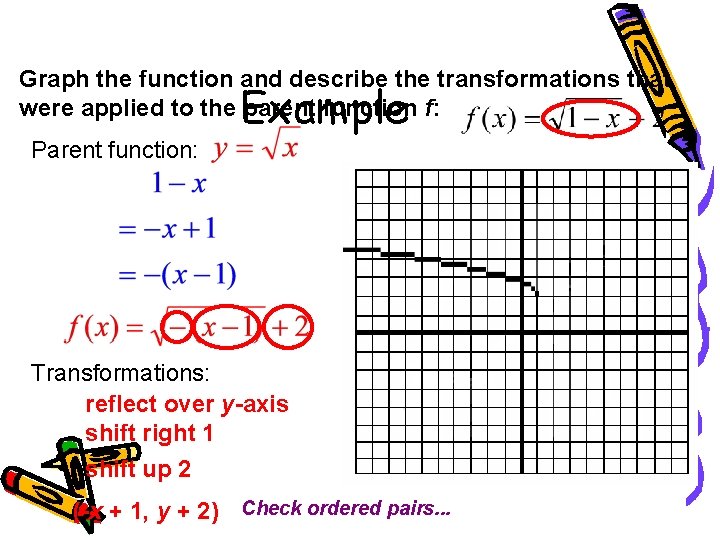
Graph the function and describe the transformations that were applied to the parent function f: Parent function: Example Transformations: reflect over y-axis shift right 1 shift up 2 (-x + 1, y + 2) Check ordered pairs. . .