Ch 2 Graphs y axis Quadrant II Quadrant

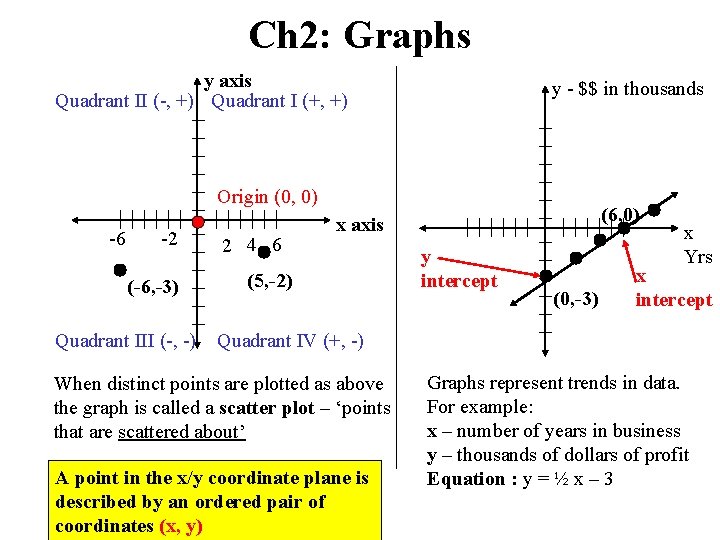
Ch 2: Graphs y axis Quadrant II (-, +) Quadrant I (+, +) y - $$ in thousands Origin (0, 0) -6 -2 (-6, -3) Quadrant III (-, -) 2 4 6 (6, 0) x axis (5, -2) y intercept (0, -3) x Yrs x intercept Quadrant IV (+, -) When distinct points are plotted as above the graph is called a scatter plot – ‘points that are scattered about’ A point in the x/y coordinate plane is described by an ordered pair of coordinates (x, y) Graphs represent trends in data. For example: x – number of years in business y – thousands of dollars of profit Equation : y = ½ x – 3

2. 1 Distance & Midpoint y Things to know: 1. Find distance or midpoint given 2 points 2. Given midpoint and 1 point, find the other point 3. Given distance and 1 point, find the other point Origin (0, 0) -6 A point in the x/y coordinate plane is described by an ordered pair of coordinates (x, y) The Distance Formula To find the distance between 2 points (x 1, y 1) and (x 2, y 2) d = (x 2 – x 1)2 + (y 2 – y 1)2 -2 2 4 6 (-6, -3) x (5, -2) The Midpoint Formula To find the coordinates of the midpoint (M) of a segment given segment endpoints of (x 1, y 1) and (x 2, y 2) M x 1 + x 2, y 1 + y 2 2 2

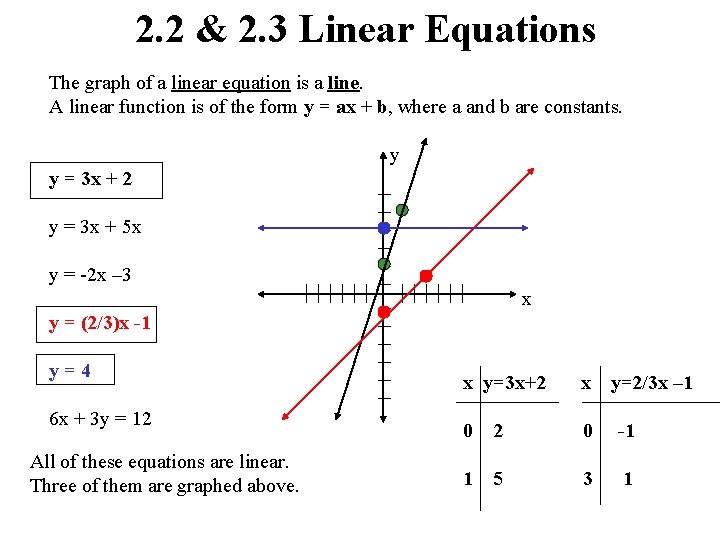
2. 2 & 2. 3 Linear Equations The graph of a linear equation is a line. A linear function is of the form y = ax + b, where a and b are constants. y y = 3 x + 2 y = 3 x + 5 x y = -2 x – 3 x y = (2/3)x -1 y=4 6 x + 3 y = 12 All of these equations are linear. Three of them are graphed above. x y=3 x+2 x y=2/3 x – 1 0 2 0 -1 1 5 3 1

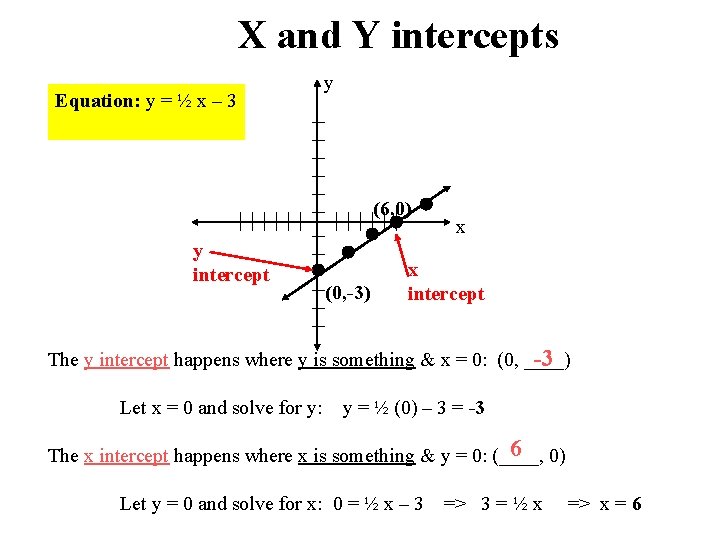
X and Y intercepts Equation: y = ½ x – 3 y (6, 0) y intercept (0, -3) x x intercept -3 The y intercept happens where y is something & x = 0: (0, ____) Let x = 0 and solve for y: y = ½ (0) – 3 = -3 6 0) The x intercept happens where x is something & y = 0: (____, Let y = 0 and solve for x: 0 = ½ x – 3 => 3 = ½ x => x = 6

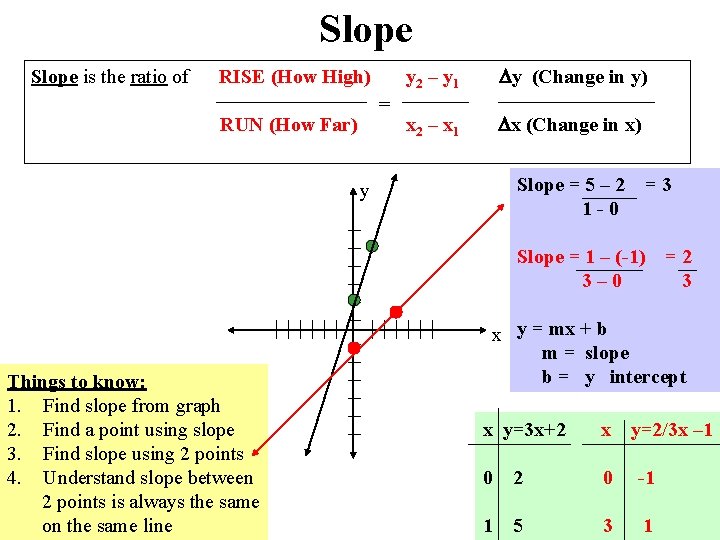
Slope is the ratio of RISE (How High) = RUN (How Far) y 2 – y 1 y (Change in y) x 2 – x 1 x (Change in x) Slope = 5 – 2 1 -0 y =3 Slope = 1 – (-1) 3– 0 Things to know: 1. Find slope from graph 2. Find a point using slope 3. Find slope using 2 points 4. Understand slope between 2 points is always the same on the same line =2 3 x y = mx + b m = slope b = y intercept x y=3 x+2 x y=2/3 x – 1 0 2 0 -1 1 5 3 1

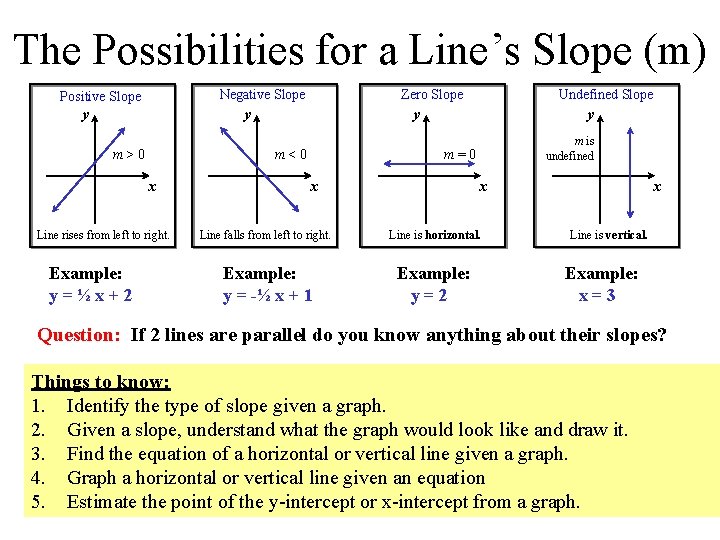
The Possibilities for a Line’s Slope (m) Negative Slope Positive Slope y y m>0 Line rises from left to right. Example: y=½x+2 y y m<0 x Undefined Slope Zero Slope m is undefined m=0 x x x Line falls from left to right. Line is horizontal. Example: y = -½ x + 1 Example: y=2 Line is vertical. Example: x=3 Question: If 2 lines are parallel do you know anything about their slopes? Things to know: 1. Identify the type of slope given a graph. 2. Given a slope, understand what the graph would look like and draw it. 3. Find the equation of a horizontal or vertical line given a graph. 4. Graph a horizontal or vertical line given an equation 5. Estimate the point of the y-intercept or x-intercept from a graph.

Linear Equation Forms (2 Vars) Standard Form Ax + By = C Things to know: 1. Graph using x/y chart 2. Know this makes a line graph. Example: 6 x + 3 y = 12 Slope Intercept Form Example: y = - ½ x - 2 Point Slope Form A, B, C are real numbers. A & B are not both 0. y = mx + b m is the slope b is the y intercept Things to know: 1. Find Slope & y-intercept 2. Graph using slope & y-intercept y – y 1 = m(x – x 1) Example: Write the linear equation through point P(-1, 4) with slope 3 y – y 1 = m(x – x 1) Things to know: y – 4 = 3(x - - 1) 1. Change from point slope to/from other forms. y – 4 = 3(x + 1) 2. Find the x or y-intercept of any linear equation

Parallel and Perpendicular Lines & Slopes Things to know: 1. Identify parallel/non-parallel lines. PARALLEL • Vertical lines are parallel • Non-vertical lines are parallel if and only if they have the same slope y=¾x+2 y = ¾ x -8 PERPENDICULAR Same Slope Things to know: 1. Identify (non) perpendicular lines. 2. Find the equation of a line parallel or perpendicular to another line through a point or through a y-intercept. • Any horizontal line and vertical line are perpendicular • If the slopes of 2 lines have a product of – 1 and/or are negative reciprocals of each other then the lines are perpendicular. y= ¾ x+2 Negative reciprocal slopes y = - 4/3 x - 5 3 • -4 = 4 3 -12 = -1 12 Product is -1

Practice Problems 1. Find the slope of a line passing through (-1, 2) and (3, 8) 2. Graph the line passing through (1, 2) with slope of - ½ 3. Is the point (2, -1) on the line specified by: y = -2(x-1) + 3 ? 4. Parallel, Perpendicular or Neither? 3 y = 9 x + 3 and 6 y + 2 x = 6 5. Find the equation of a line parallel to y = 4 x + 2 through the point (-1, 5) 6. Find the equation of a line perpendicular to y = - ¾ x – 8 through point (2, 7) 7. 8. Find a line parallel to x = 7; Find a line perpendicular to x = 7 Find a line parallel to y = 2; Find a line perpendicular to y = 2 9. 8. Graph (using an x/y chart – plotting points) and find intercepts of 10. any equation such as: y = 2 x + 5 or y = x 2 – 4

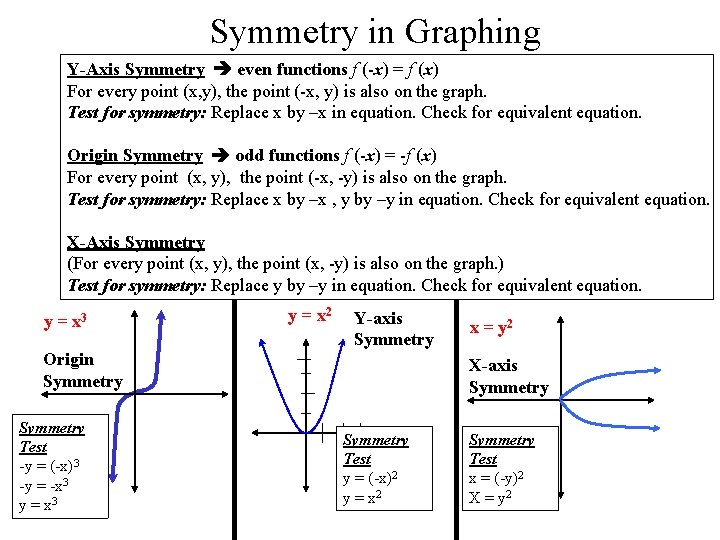
Symmetry in Graphing Y-Axis Symmetry even functions f (-x) = f (x) For every point (x, y), the point (-x, y) is also on the graph. Test for symmetry: Replace x by –x in equation. Check for equivalent equation. Origin Symmetry odd functions f (-x) = -f (x) For every point (x, y), the point (-x, -y) is also on the graph. Test for symmetry: Replace x by –x , y by –y in equation. Check for equivalent equation. X-Axis Symmetry (For every point (x, y), the point (x, -y) is also on the graph. ) Test for symmetry: Replace y by –y in equation. Check for equivalent equation. y = x 3 Origin Symmetry Test -y = (-x)3 -y = -x 3 y = x 2 Y-axis Symmetry x = y 2 X-axis Symmetry Test y = (-x)2 y = x 2 Symmetry Test x = (-y)2 X = y 2

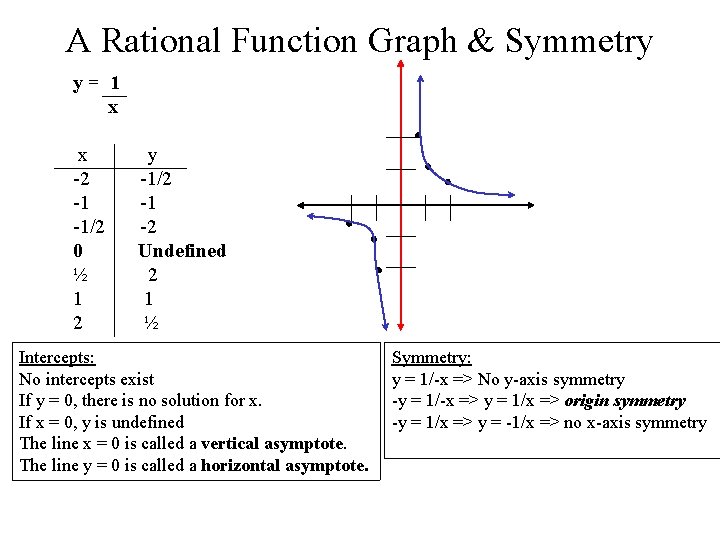
A Rational Function Graph & Symmetry y= 1 x x -2 -1 -1/2 0 ½ 1 2 y -1/2 -1 -2 Undefined 2 1 ½ Intercepts: No intercepts exist If y = 0, there is no solution for x. If x = 0, y is undefined The line x = 0 is called a vertical asymptote. The line y = 0 is called a horizontal asymptote. Symmetry: y = 1/-x => No y-axis symmetry -y = 1/-x => y = 1/x => origin symmetry -y = 1/x => y = -1/x => no x-axis symmetry

Application: Solar Energy • The solar electric generating systems at Kramer Junction, California, use parabolic troughs to heat a heat-transfer fluid to a high temperature. This fluid is used to generate steam that drives a power conversion system to produce electricity. For troughs, 7. 5 feet wide, an equation for the cross-section is: 16 y 2 = 120 x – 225 • (a) Find the intercepts of the graph of the equation • (b) Test for symmetry with respect to the x-axis, y-axis, and origin

Application: Cigarette Use A study by the Partnership for a Drug-Free America indicated that, in 1998, 42% of teens in grades 7 through 12 had recently used cigarettes. A similar study in 2005 indicated that 22% of such teens had recently used cigarettes. (a) Write a linear equation that relates the percent of teens y to the number of years after 1998, x. (a) Find the intercepts of the graph of your equation. (b) Do the intercepts have any meaningful interpretation? (c) Use your equation to predict the percent for the year 2019. Is this result reasonable?

2. 5 Proportions & Variation Proportion equality of 2 ratios. Proportions are used to solve problems in everyday life. 1. If someone earns $100 per day, then how many dollars can the person earn in 5 days? 100 x (x)(1) = (100)(5) = 5 1 x = 500 2. If a car goes 210 miles on 10 gallons of gas, the car can go 420 miles on X gallons 210 10 3. = 420 x (210)(x) = (420)(10) (210)(x) = 4200 x = 4200 / 210 = 20 gallons If a person walks a mile in 16 min. , that person can walk a half mile in x min. 16 1 = x ½ (x)(1) = ½(16) x = 8 minutes

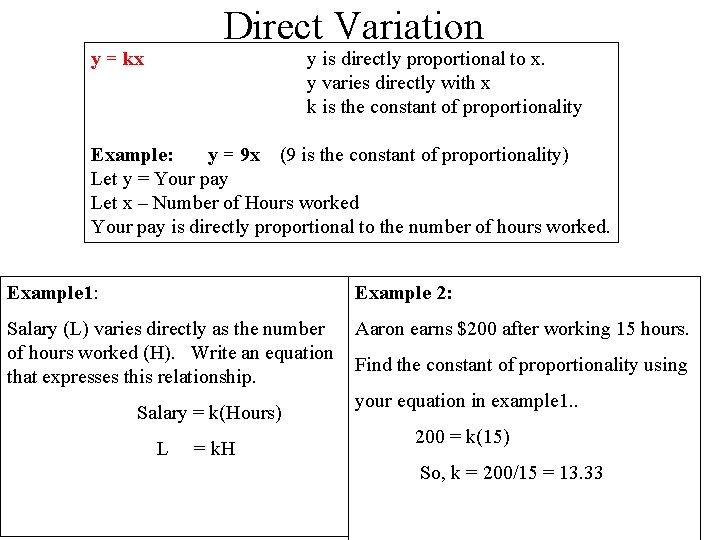
Direct Variation y = kx y is directly proportional to x. y varies directly with x k is the constant of proportionality Example: y = 9 x (9 is the constant of proportionality) Let y = Your pay Let x – Number of Hours worked Your pay is directly proportional to the number of hours worked. Example 1: Example 2: Salary (L) varies directly as the number of hours worked (H). Write an equation that expresses this relationship. Aaron earns $200 after working 15 hours. Salary = k(Hours) L = k. H Find the constant of proportionality using your equation in example 1. . 200 = k(15) So, k = 200/15 = 13. 33

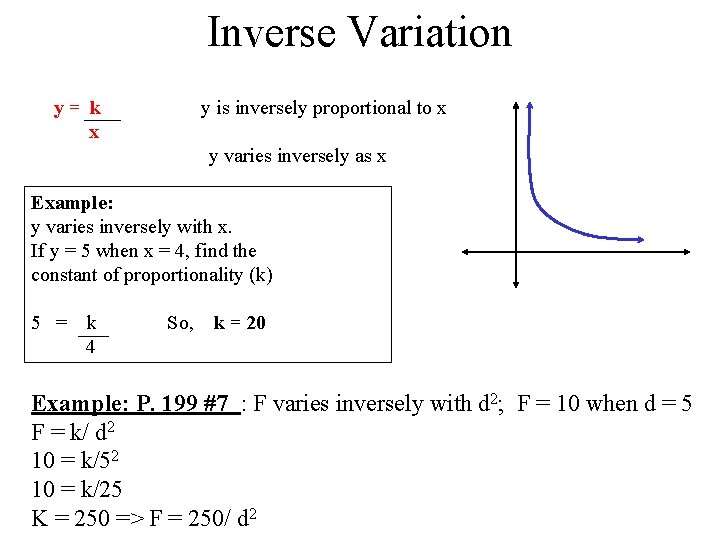
Inverse Variation y= k x y is inversely proportional to x y varies inversely as x Example: y varies inversely with x. If y = 5 when x = 4, find the constant of proportionality (k) 5 = k 4 So, k = 20 Example: P. 199 #7 : F varies inversely with d 2; F = 10 when d = 5 F = k/ d 2 10 = k/52 10 = k/25 K = 250 => F = 250/ d 2

Another Example (Inverse Variation) y= k x y is inversely proportional to x y varies inversely as x P. 197: Example 2: The maximum weight W that can be safely supported by a 2 -inch by 4 -inch piece of point varies inversely with its length L. Experimenters indicate that the maximum weight that a 10 foot long 2 x 4 Piece of pine can support is 500 lbs. Write a general formula relating the Maximum weight W that can be safely supported by a length of 25 feet. W = k/L So, 500 = k/10 => k = 5000 Thus, W = 5000/L So, Maximum weight safely supported for Length of 25 ft is: W = 5000/25 = 200 lbs.

Direct Variation with Power y = kxn y is directly proportional to the nth power of x Example: Distance varies directly as the square of the time (t) Distance = kt 2 D = kt 2 Joint Variation y = kxp • y varies jointly as x and p

Example: (Joint Variation) y = kxp • y varies jointly as x and p P. 198 Example 4: The force F of the wind on a flat surface positioned at a right angle To the direction of the wind varies jointly with the area A of the Surface and the square of the speed v of the wind. A wind of 30 miles per hour blowing on a window measuring 4 ft By 5 ft has a force of 150 lbs. What is the force on a window measuring 3 ft by 4 ft caused by a wind of 50 mph? F = k. Av 2 A = 4 x 5 = 20 v = 30 150 = k (20)(900) 150 = 18000 k K = 150/18000 = 1/120 F = (1/120)Av 2 , so, when wind = 50 mph on 3 x 4 (A = 12), F = (1/120)(12)(2500) = 250 lbs

Example: Combined Variation P. 199 S#13 The square of T varies directly with the cube of A and Inversely with the square of D T = 2 when A = 2 and D = 4. Write a general formula to describe each variation T 2 = k. A 3 D 2 Thus, T 2 = 8 A 3 D 2 4 = k(8) 16 8 k = 64 k = 8