Ch 2 3 Real life applications of parabolas

Ch 2. 3

Real life applications of parabolas • What do you know about satellite dishes? • How do they work? • The essential piece is that the satellite dish is an antenna that receives electromagnetic signals from an orbiting satellite. The shape of the satellite dish is parabolic.

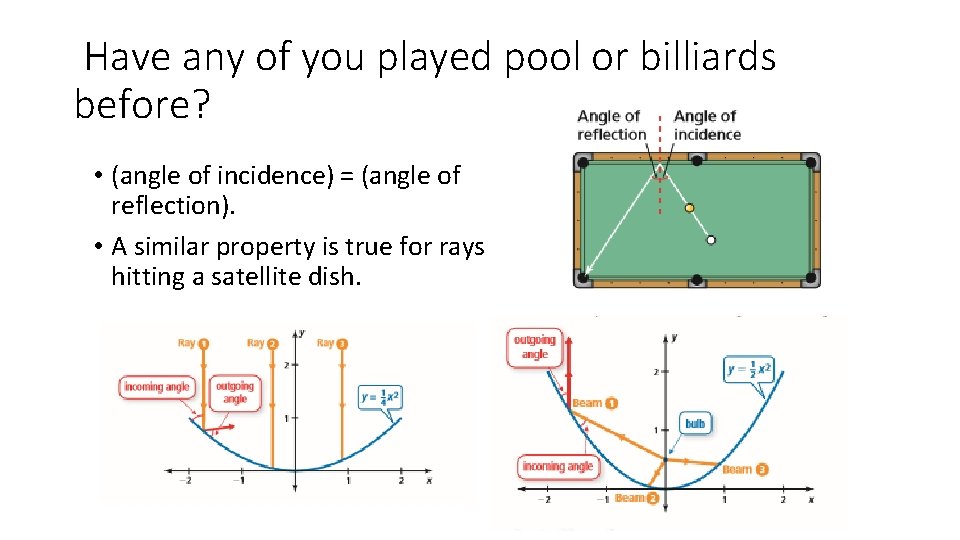
Have any of you played pool or billiards before? • (angle of incidence) = (angle of reflection). • A similar property is true for rays hitting a satellite dish.

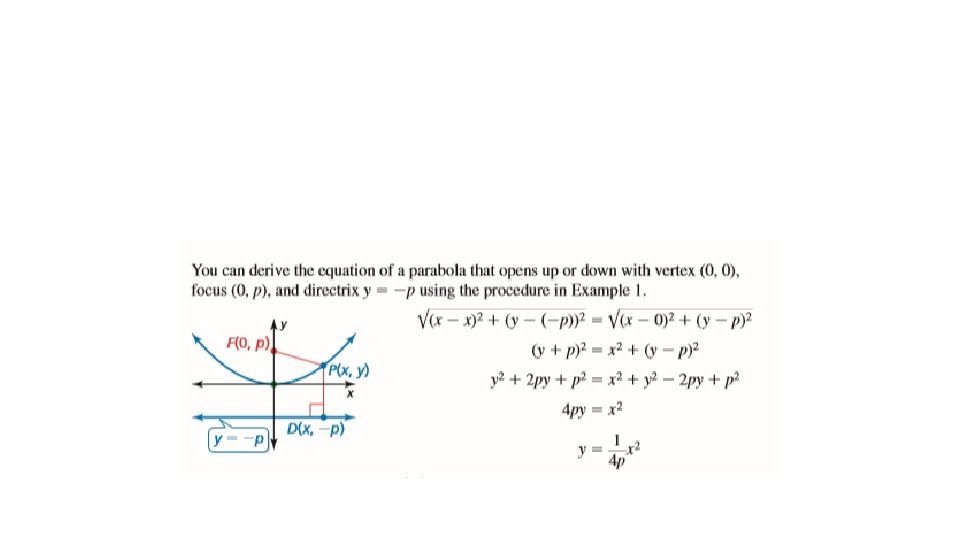
How else can a parabola be defined? • Previously, you learned that the graph of a quadratic function is a parabola that opens up or down. • A parabola can also be defined as the set of all points (x, y) in a plane that are equidistant from a fixed point called the focus and a fixed line called the directrix.

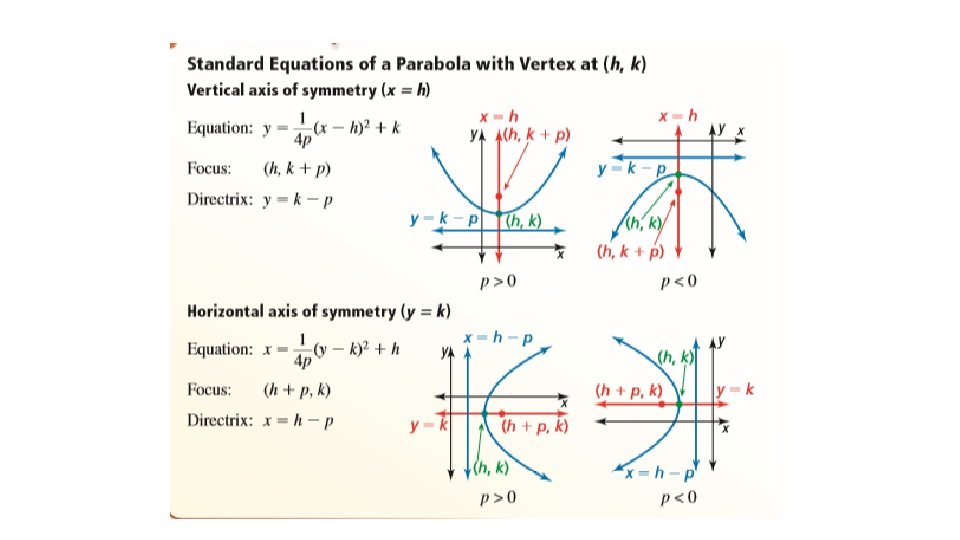
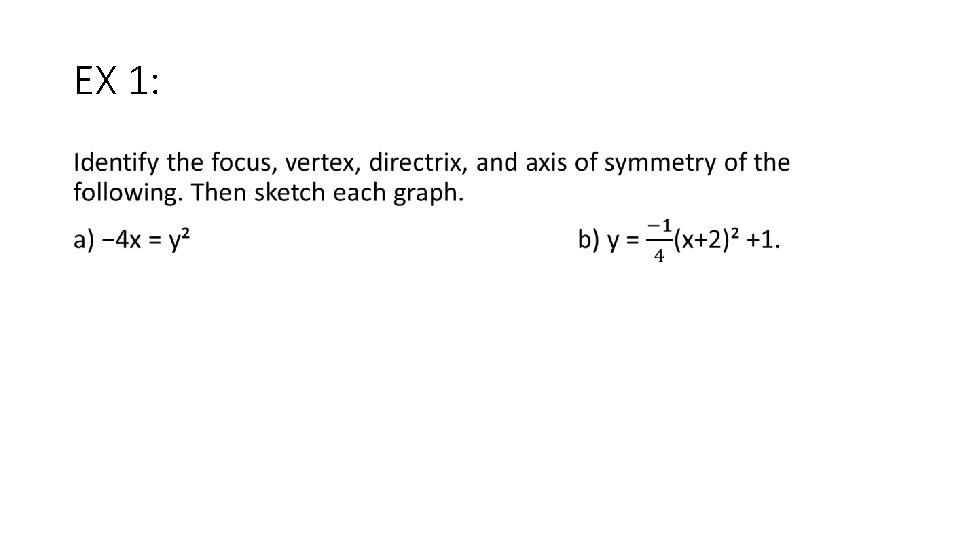
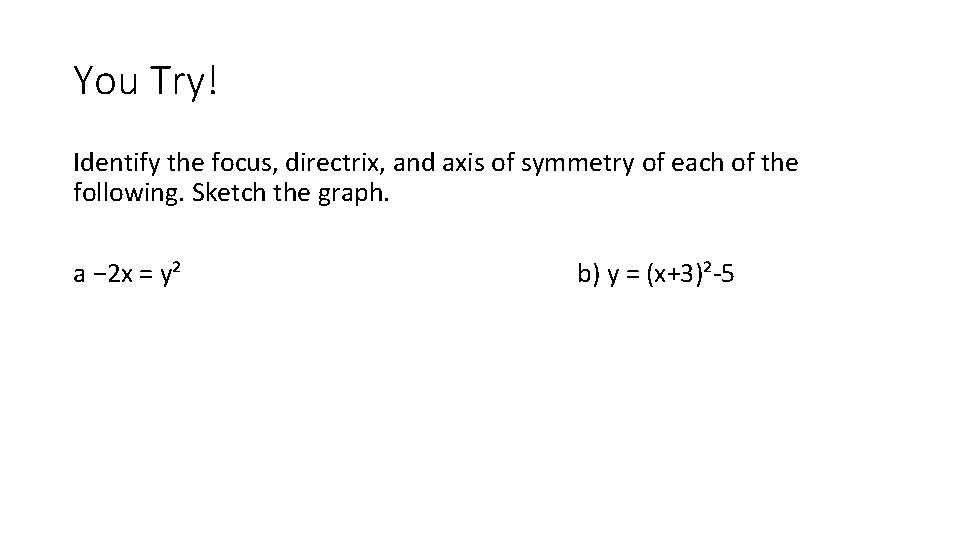
You Try! Identify the focus, directrix, and axis of symmetry of each of the following. Sketch the graph. a − 2 x = y² b) y = (x+3)²-5

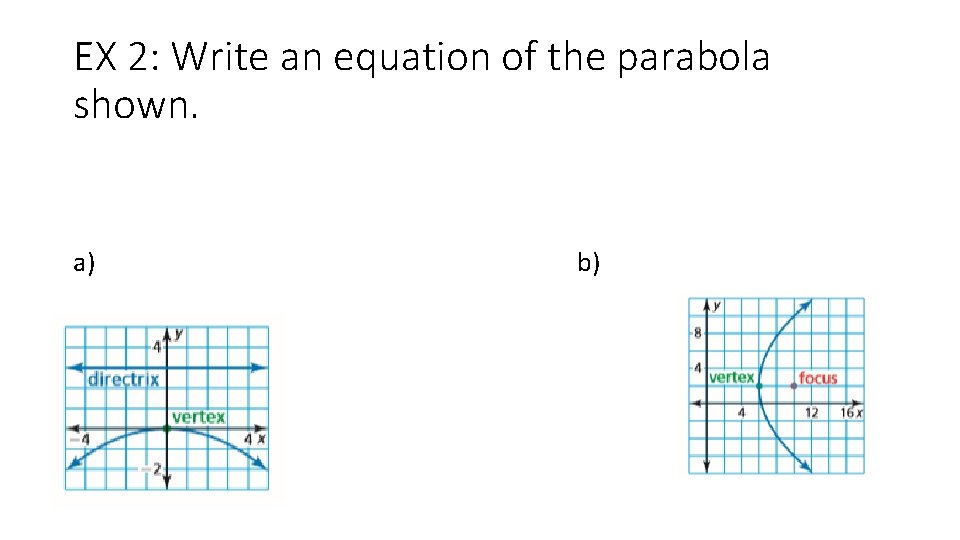
EX 2: Write an equation of the parabola shown. a) b)

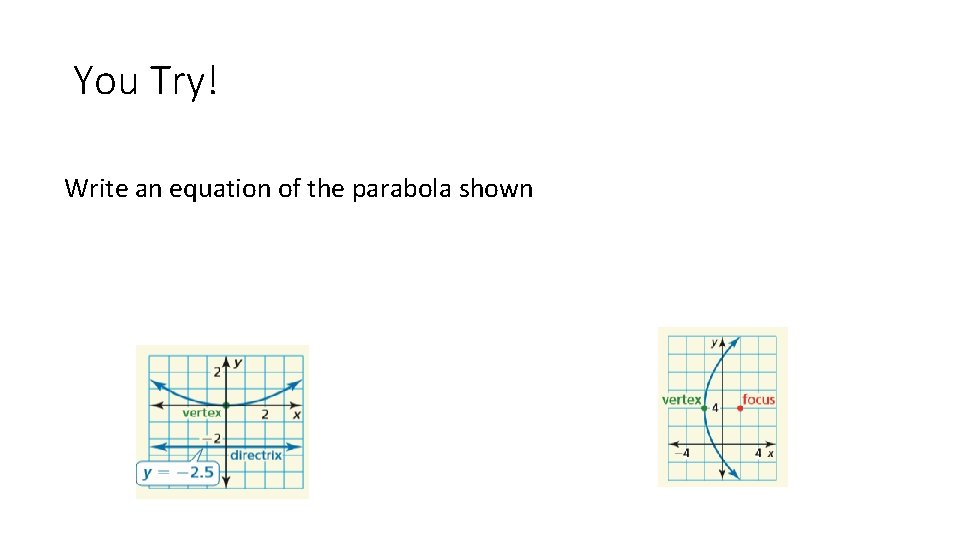
You Try! Write an equation of the parabola shown

EX 3: Modeling with parabolas and the focus An electricity-generating dish uses a parabolic reflector to concentrate sunlight onto a high-frequency engine located at the focus of the reflector. (The sunlight heats helium to 650°C to power the engine. ) Write an equation that represents the cross section of the dish shown with its vertex at (0, 0). What is the depth of the dish?

You Try! An archway in front of a school is in the shape of a parabola. The top of the arch is the vertex (0, 0). The school seal is at the focus, 2. 5 feet below the vertex, and the arch is 18 feet wide at the ground. Write an equation that represents a cross section of the arch. What is the height from the top of the arch to the ground?

Pg 72 #11, 12, 13, 17, 23, 25, -31 odd, 37, 41, 43, 49