Ch 19 Harmonic Motion 19 1 Harmonic Motion

Ch. 19 Harmonic Motion

19. 1 – Harmonic Motion • Linear motion is shown by a bicycle moving in a straight line. • Harmonic motion is motion that repeats. Ex: pedaling a bike, swinging on a swing, etc. • A cycle is a unit of motion that repeats over and over. Ex: a full turn of a wheel, a full back-and-forth swing

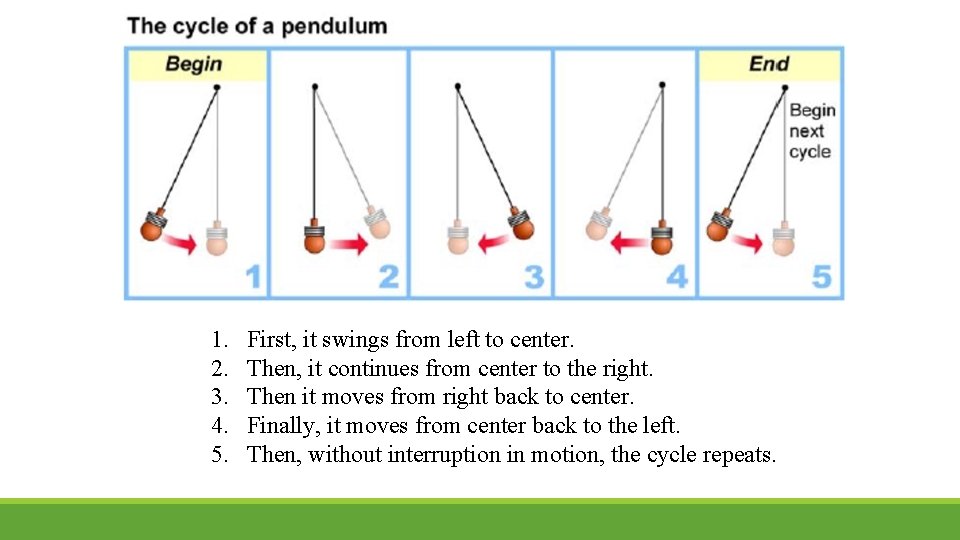
1. 2. 3. 4. 5. First, it swings from left to center. Then, it continues from center to the right. Then it moves from right back to center. Finally, it moves from center back to the left. Then, without interruption in motion, the cycle repeats.

• An oscillation is a motion that repeats regularly. • A system with harmonic motion is an oscillator. Ex: a pendulum, your heart, the solar system, an atom • Vibration is another term used for back and forth. • Earth is part of several oscillating systems: - The Earth-sun system’s cycle is a year. - The Earth-moon system’s cycle lasts ~28 days. - Earth rotates every 24 hours. - Earth’s axis wobbles in cycles of 22, 000 years.

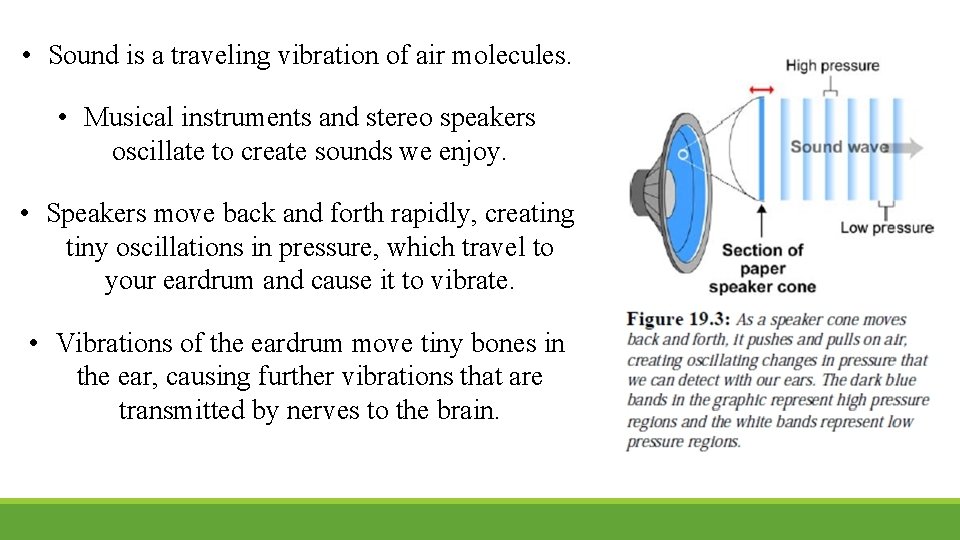
• Sound is a traveling vibration of air molecules. • Musical instruments and stereo speakers oscillate to create sounds we enjoy. • Speakers move back and forth rapidly, creating tiny oscillations in pressure, which travel to your eardrum and cause it to vibrate. • Vibrations of the eardrum move tiny bones in the ear, causing further vibrations that are transmitted by nerves to the brain.

• Light is the result of harmonic motion of electric and magnetic fields. • The picture’s colors come from the vibration of electrons in the molecules of paint. Each paint color contains molecules that oscillate with different cycles to create the various colors of light you see.

• Modern communication technology relies on harmonic motion. • The electronic technology in a cell phone uses an oscillator that makes more than 100 million cycles each second! • When tuning into a station at 101 on the FM dial, you actually set the radio’s oscillator to 101, 000 cycles per second!

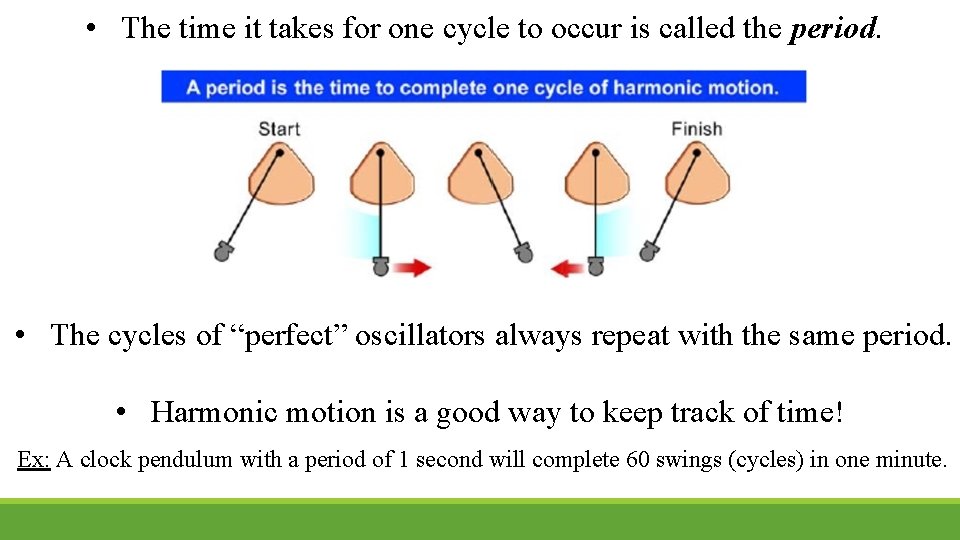
• The time it takes for one cycle to occur is called the period. • The cycles of “perfect” oscillators always repeat with the same period. • Harmonic motion is a good way to keep track of time! Ex: A clock pendulum with a period of 1 second will complete 60 swings (cycles) in one minute.

• The term frequency means the number of cycles per second. • The unit for frequency: Hertz (Hz); 1 Hz = 1 cycle per second • FM (frequency modulation) radio frequencies: 95 – 107 million Hz • Your heartbeat’s frequency: ½ – 2 Hz • The musical note A’s frequency: 440 Hz • The human voice’s frequency range: mainly 100 – 2, 000 Hz

• A radio station dial set to 101 FM receives music broadcast at a frequency of 101, 000 Hz (101 megahertz). • The human ear can hear sound frequencies ranging from 20 Hz to between 15, 000 and 20, 000 Hz! • The Hz is a unit that is the same in both English and metric systems.

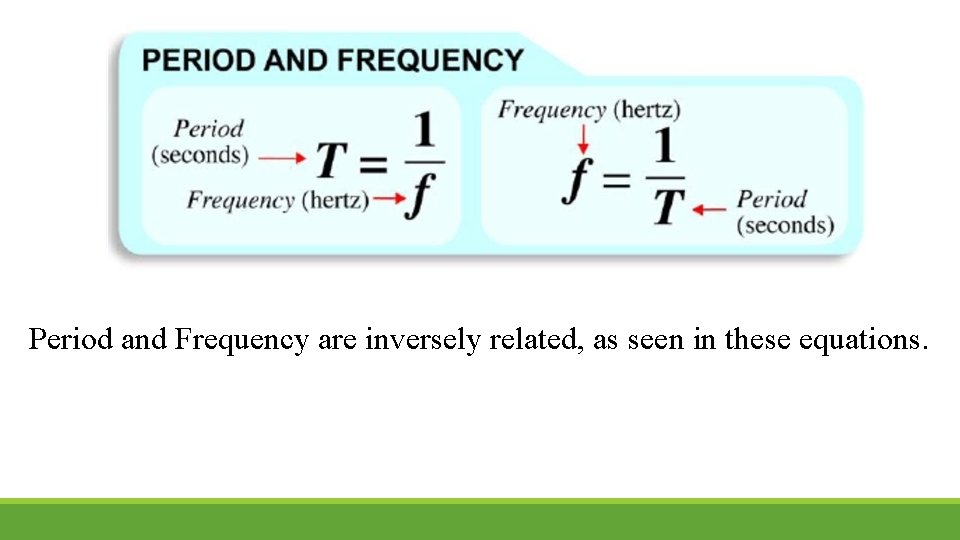
• Frequency and period are inversely related. • Period: the time it takes for one cycle • Frequency: the number of cycles per unit time. • Ex: If the period of a pendulum is 2 seconds, the frequency is ½ Hz. Explanation: It takes 2 seconds for the pendulum to swing back and forth 1 cycle. Therefore it only swings ½ a cycle per second.

Period and Frequency are inversely related, as seen in these equations.

Amplitude: • describes the “size” of a cycle • Is the maximum distance the oscillator moves away from its equilibrium position • can be measured in distances or angles • can also be voltage or pressure, depending on the oscillation • is measured in units appropriate to the system

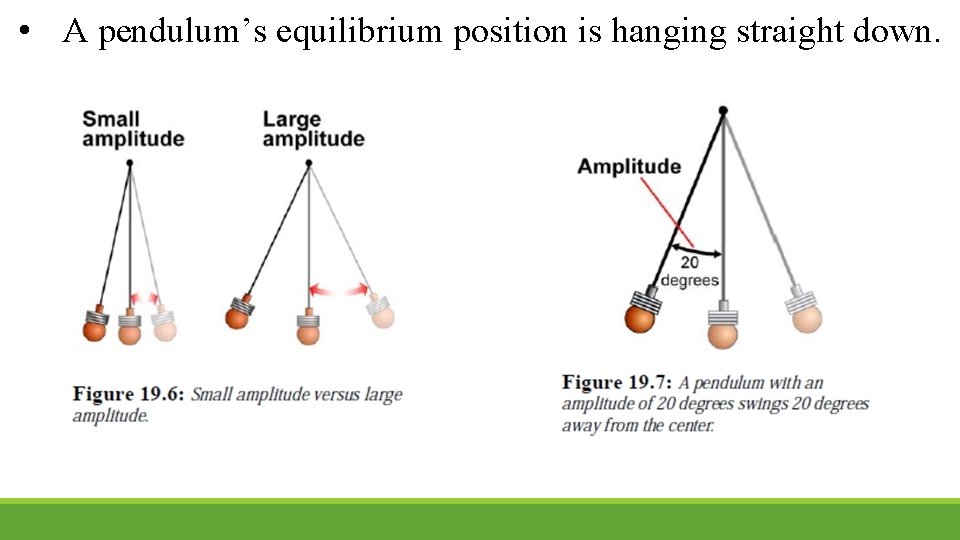
• A pendulum’s equilibrium position is hanging straight down.

• Friction slows down a pendulum, as it does all oscillators. • The pendulum slows until it hangs straight down, motionless. • Dampening is the gradual loss of amplitude of an oscillator. • Clocks using pendulums have to take dampening into account and add energy to counteract it.

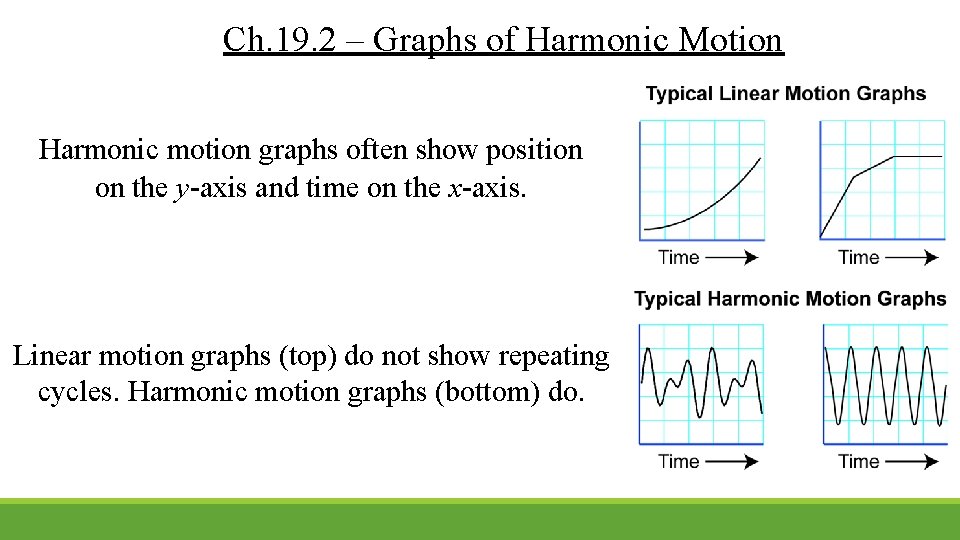
Ch. 19. 2 – Graphs of Harmonic Motion Harmonic motion graphs often show position on the y-axis and time on the x-axis. Linear motion graphs (top) do not show repeating cycles. Harmonic motion graphs (bottom) do.

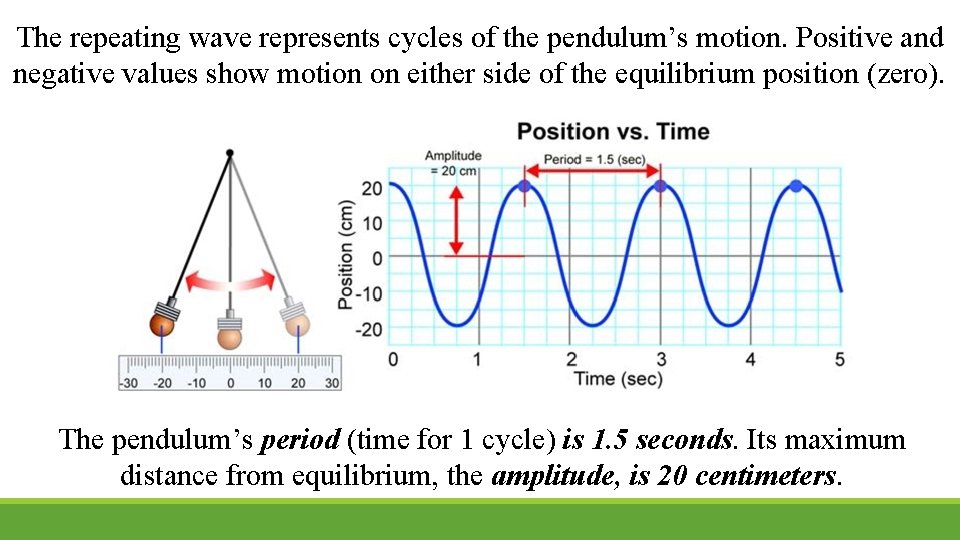
The repeating wave represents cycles of the pendulum’s motion. Positive and negative values show motion on either side of the equilibrium position (zero). The pendulum’s period (time for 1 cycle) is 1. 5 seconds. Its maximum distance from equilibrium, the amplitude, is 20 centimeters.

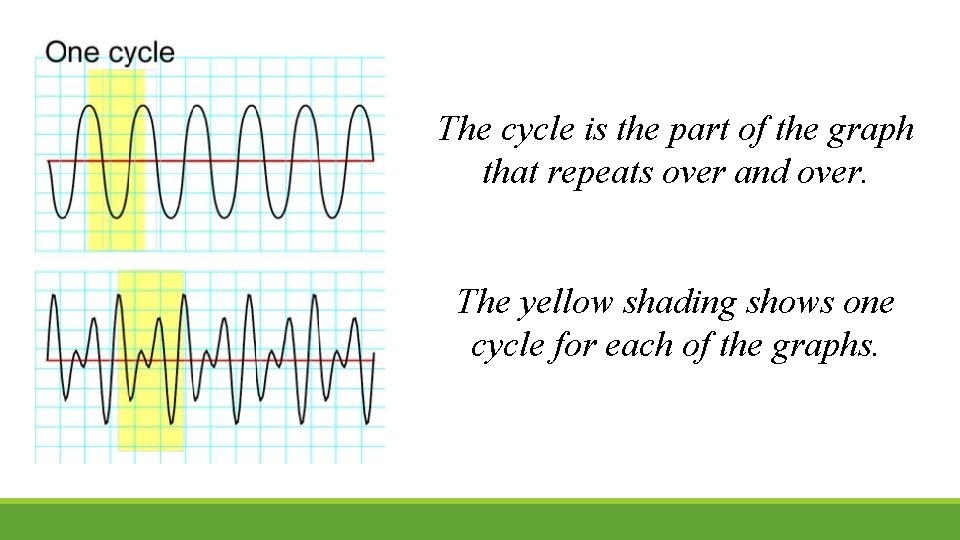
The cycle is the part of the graph that repeats over and over. The yellow shading shows one cycle for each of the graphs.

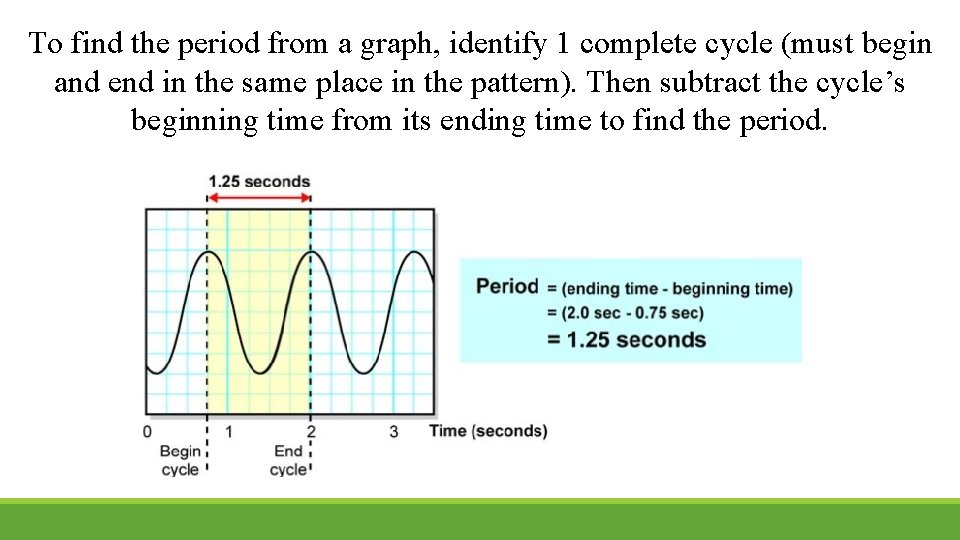
To find the period from a graph, identify 1 complete cycle (must begin and end in the same place in the pattern). Then subtract the cycle’s beginning time from its ending time to find the period.

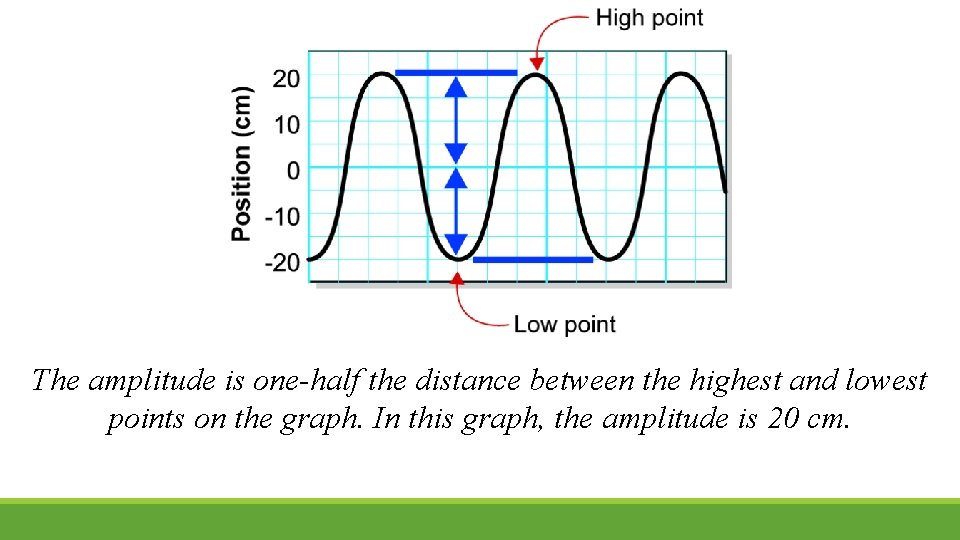
The amplitude is one-half the distance between the highest and lowest points on the graph. In this graph, the amplitude is 20 cm.

In equation form, Amplitude is:

Phase: - describes where an oscillator is in its cycle - is measured relative to the whole cycle - is independent of amplitude or period - is useful when comparing 2 or more oscillators - is measured in degrees (complete cycle = 360 )

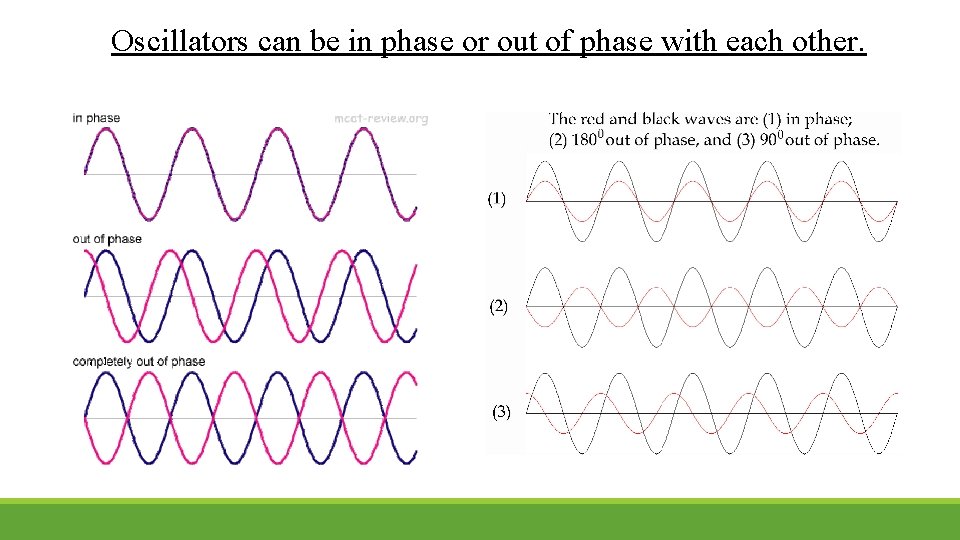
Oscillators can be in phase or out of phase with each other.

• Harmonic motion of a rotating turntable is shown by the back-and-forth motion of the peg’s shadow • Circular motion is harmonic because rotation is a pattern of repeating cycles that measure 360. • Repetitive cycles can be compared to circular motion, so we use degrees to measure phase.

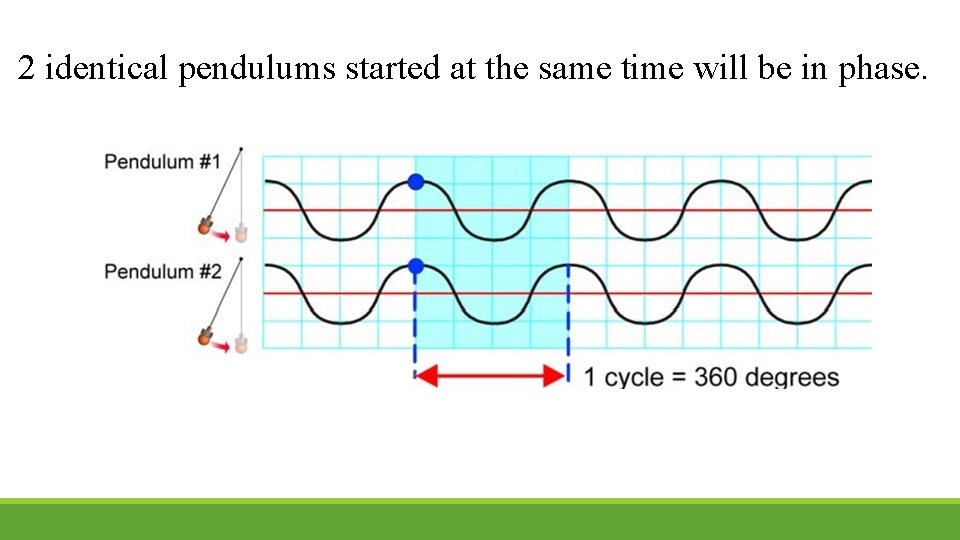
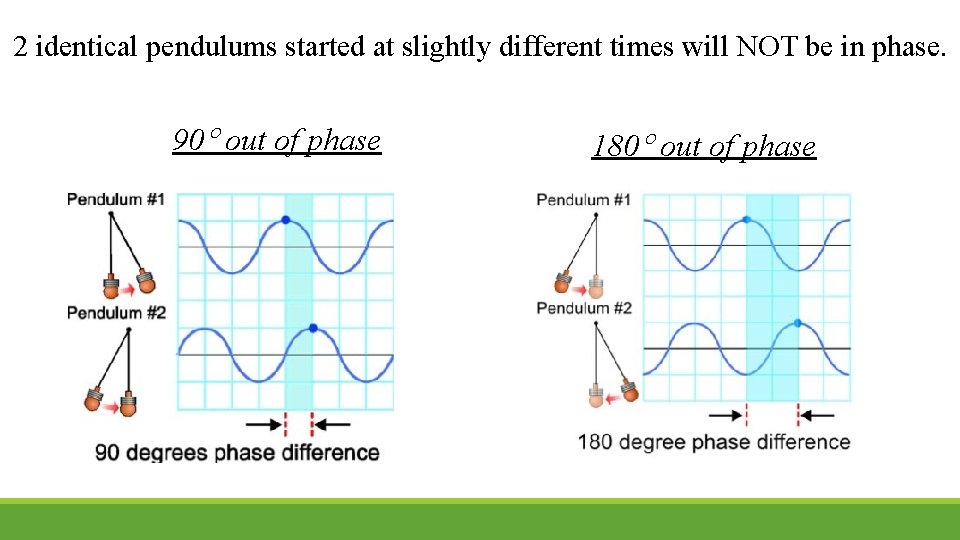
2 identical pendulums started at the same time will be in phase.

2 identical pendulums started at slightly different times will NOT be in phase. 90 out of phase 180 out of phase

https: //www. youtube. com/watch? v=y. Vkdf. J 9 Pk. RQ

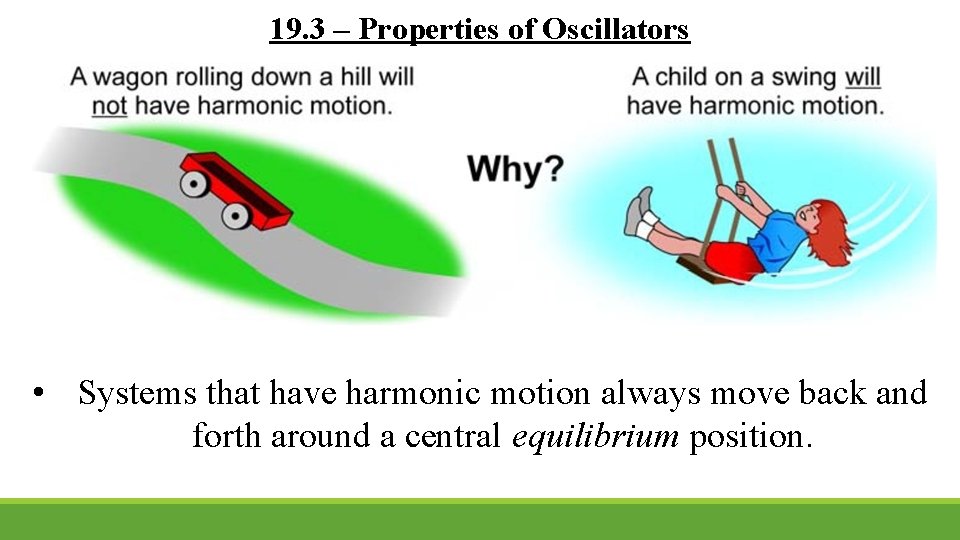
19. 3 – Properties of Oscillators • Systems that have harmonic motion always move back and forth around a central equilibrium position.

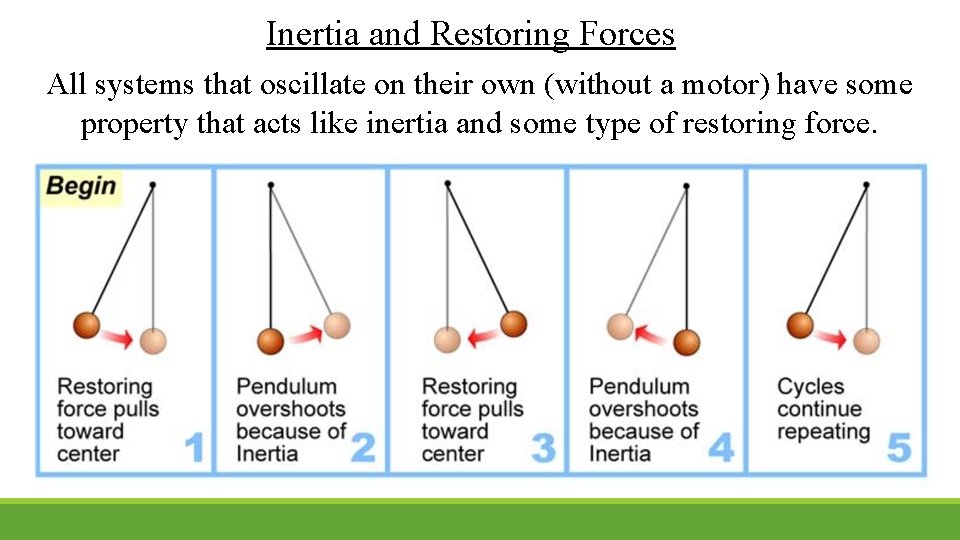
Restoring forces: • always pull a system back toward equilibrium • keep a pendulum swinging • are related to weight and the lift force (or tension) of the string of a pendulum

Inertia and Restoring Forces All systems that oscillate on their own (without a motor) have some property that acts like inertia and some type of restoring force.

You can make a simple oscillator with 2 rubber bands and a washer. What happens to the oscillator’s period if you add more washers? The rubber band’s restoring force hasn’t changed, so increasing the mass will decrease acceleration and make the period longer.

• Changing a pendulum’s mass does NOT affect its period, but changing its length does! • Gravity is the pendulum’s restoring force, so adding mass increases inertia by an amount exactly equal to the added force from gravity. • The heavier pendulum’s acceleration stays the same, so its period doesn’t change. • Changing an oscillator’s mass will only change its period when the restoring force is NOT due to gravity!

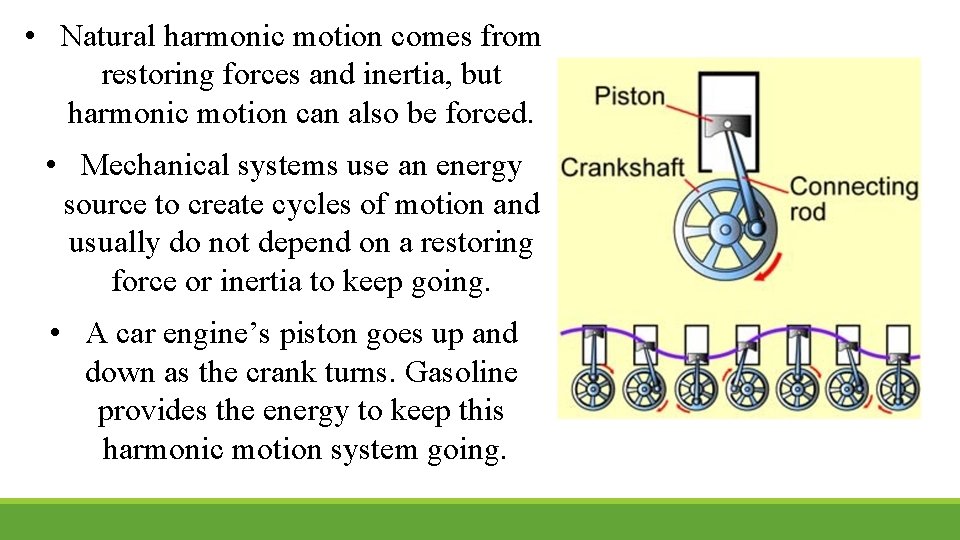
• Natural harmonic motion comes from restoring forces and inertia, but harmonic motion can also be forced. • Mechanical systems use an energy source to create cycles of motion and usually do not depend on a restoring force or inertia to keep going. • A car engine’s piston goes up and down as the crank turns. Gasoline provides the energy to keep this harmonic motion system going.

• Every oscillating system (anything that vibrates) has a natural frequency. • Most oscillate in multiple ways, so they have several natural frequencies. Natural frequency: - is the frequency at which a system naturally oscillates - depends on the balance of restoring forces and inertia (mass) - can be changed if the balance of restoring forces and inertia is changed

A guitar uses the natural frequency of strings to make musical notes. For the musical note A, the string vibrates at 440 hertz.

Periodic force: - is repeated over and over (Ex: pushing a swing) - has cycles with amplitudes, frequencies, and periods - is required to supply energy to an oscillator - produces resonance when it matches the oscillator’s natural frequency Resonance occurs when: 1. ) There is a system in harmonic motion. 2. ) There is a periodic force. 3. ) The force’s frequency matches the system’s natural frequency.

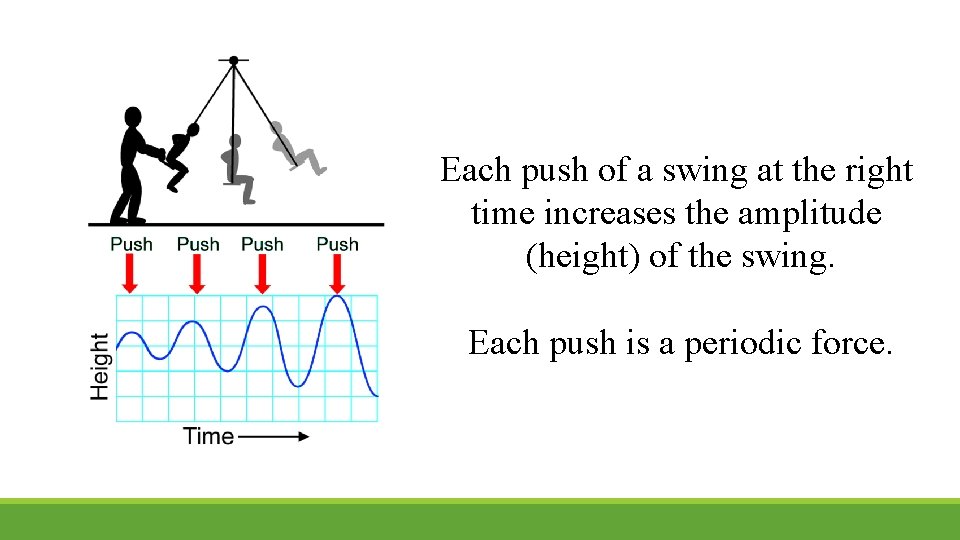
Each push of a swing at the right time increases the amplitude (height) of the swing. Each push is a periodic force.

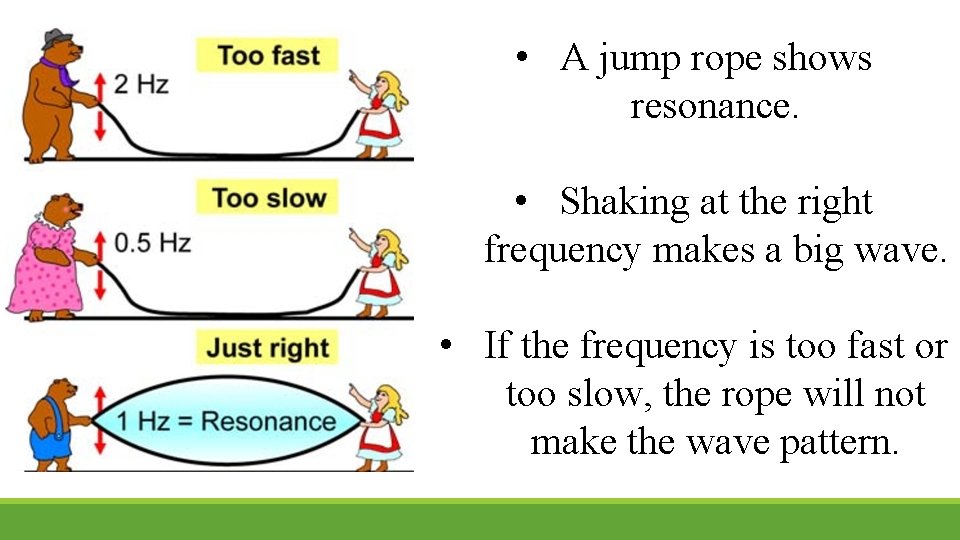
• A jump rope shows resonance. • Shaking at the right frequency makes a big wave. • If the frequency is too fast or too slow, the rope will not make the wave pattern.

When you push someone on a swing, you are using resonance. Small or big pushes at the right time in a swing’s motion will make a person swing higher. If the periodic force (the push) is applied at the wrong time, the swing does not swing at all.

• A mass on a spring is an oscillating system. • The push-pull of the spring is a restoring force. • The mass supplies the inertia. • When compressed, the spring pushes back on the mass to return to equilibrium. • When extended, the spring pulls the mass back toward equilibrium.

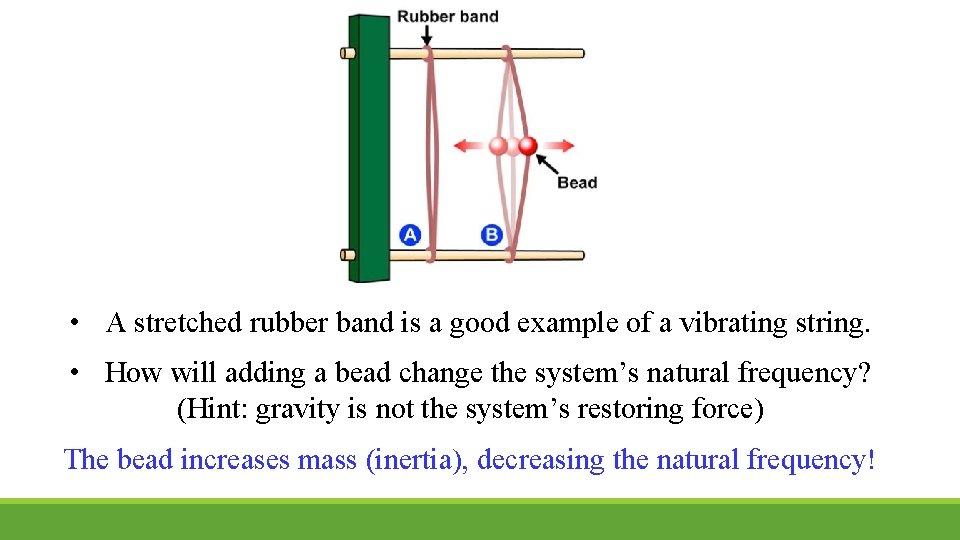
• A stretched rubber band is a good example of a vibrating string. • How will adding a bead change the system’s natural frequency? (Hint: gravity is not the system’s restoring force) The bead increases mass (inertia), decreasing the natural frequency!