CH 160 General Chemistry II Lecture Presentation Solubility

CH 160 General Chemistry II Lecture Presentation Solubility Equilibria Chapter 17 6/12/2021 Chapter 17 1

Why Study Solubility Equilibria? Many natural processes involve precipitation or dissolution of salts. A few examples: Dissolving of underground limestone deposits (Ca. CO 3) forms caves Note: Limestone is water “insoluble” (How can this be? ) Precipitation of limestone (Ca. CO 3) forms stalactites and stalagmites in underground caverns Precipitation of insoluble Ca 3(PO 4)2 and/or Ca. C 2 O 4 in the kidneys forms kidney stones Dissolving of tooth enamel, Ca 5(PO 4)3 OH, leads to tooth decay (ouch!) Precipitation of sodium urate, Na 2 C 5 H 2 N 4 O 2, in joints results in gouty arthritis. 6/12/2021 Chapter 17 2

Why Study Solubility Equilibria? Many chemical and industrial processes involve precipitation or dissolution of salts. A few examples: Production/synthesis of many inorganic compounds involves their precipitation reactions from aqueous solution Separation of metals from their ores often involves dissolution Qualitative analysis, i. e. identification of chemical species in solution, involves characteristic precipitation and dissolution reactions of salts Water treatment/purification often involves precipitation of metals as insoluble inorganic salts Toxic Pb 2+, Hg 2+, Cd 2+ removed as their insoluble sulfide (S 2 -) salts PO 43 - removed as insoluble calcium salts Precipitation of gelatinous insoluble Al(OH)3 removes suspended matter in water 6/12/2021 Chapter 17 3

Why Study Solubility Equilibria? To understand precipitation/dissolution processes in nature, and how to exploit precipitation/dissolution processes for useful purposes, we need to look at the quantitative aspects of solubility and solubility equilibria. 6/12/2021 Chapter 17 4

Solubility of Ionic Compounds Solubility Rules general rules for predicting the solubility of ionic compounds strictly qualitative 6/12/2021 Chapter 17 5

Solubility of Ionic Compounds Solubility Rule Examples All alkali metal compounds are soluble Most hydroxide compounds are insoluble. The exceptions are the alkali metals, Ba 2+, and Ca 2+ Most compounds containing chloride are soluble. The exceptions are those with Ag+, Pb 2+, and Hg 22+ All chromates are insoluble, except those of the alkali metals and the NH 4+ ion 6/12/2021 Chapter 17 6

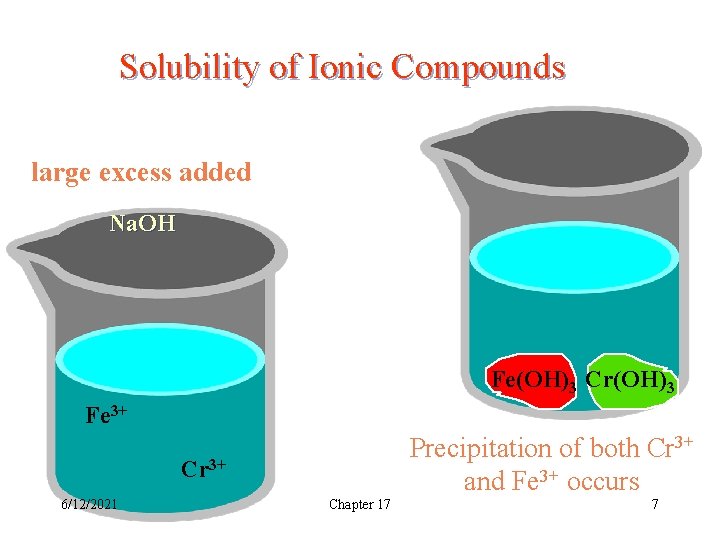
Solubility of Ionic Compounds large excess added + Na. OH Fe(OH)3 Cr(OH)3 Fe 3+ Precipitation of both Cr 3+ and Fe 3+ occurs Cr 3+ 6/12/2021 Chapter 17 7

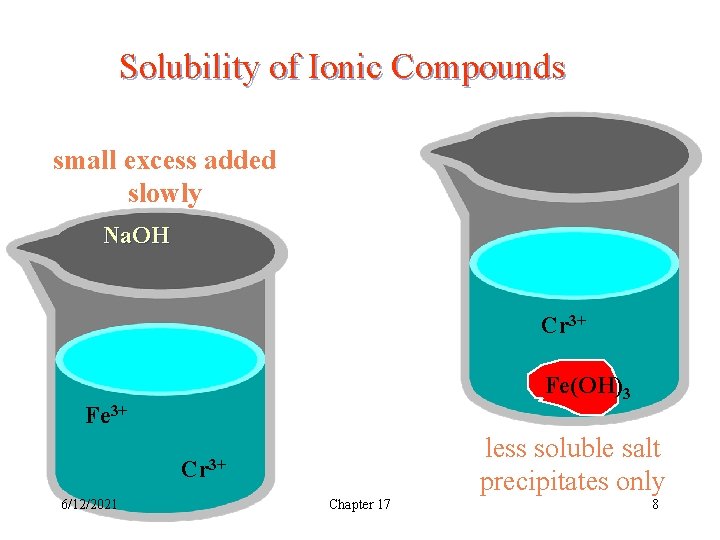
Solubility of Ionic Compounds small excess added slowly + Na. OH Cr 3+ Fe(OH)3 Fe 3+ less soluble salt precipitates only Cr 3+ 6/12/2021 Chapter 17 8

Solubility of Ionic Compounds Solubility Rules general rules for predicting the solubility of ionic compounds strictly qualitative Do not tell “how” soluble Not quantitative 6/12/2021 Chapter 17 9

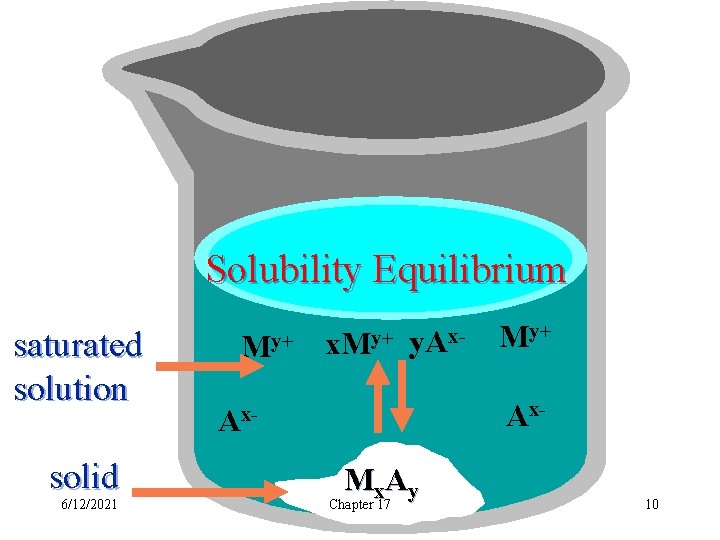
Solubility Equilibrium saturated solution solid 6/12/2021 My+ x. My+ y. Ax- My+ Ax- Ax. Mx. Ay Chapter 17 10

Solubility of Ionic Compounds Solubility Equilibrium Mx. Ay(s) <=> x. My+(aq) + y. Ax-(aq) The equilibrium constant for this reaction is the solubility product, Ksp: Ksp = [My+]x[Ax-]y 6/12/2021 Chapter 17 11

Solubility Product, Ksp is related to molar solubility 6/12/2021 Chapter 17 12

Solubility Product, Ksp is related to molar solubility qualitative comparisons 6/12/2021 Chapter 17 13

Solubility Product, Ksp used to compare relative solubilities smaller Ksp = less soluble larger Ksp= more soluble 6/12/2021 Chapter 17 14

Solubility Product, Ksp is related to molar solubility qualitative comparisons quantitative calculations 6/12/2021 Chapter 17 15

Calculations with Ksp Basic steps for solving solubility equilibrium problems Write the balanced chemical equation for the solubility equilibrium and the expression for Ksp Derive the mathematical relationship between Ksp and molar solubility (x) Make an ICE table Substitute equilibrium concentrations of ions into Ksp expression Using Ksp, solve for x or visa versa, depending on what is wanted and the information provided 6/12/2021 Chapter 17 16

Example 1 (1 on Example Problems Handout) Calculate the Ksp for Mg. F 2 if the molar solubility of this salt is 2. 7 x 10 -3 M. (ans. : 7. 9 x 10 -8) 6/12/2021 Chapter 17 17

Example 2 (2 on Example Problems Handout) Calculate the Ksp for Ca 3(PO 4)2 (FW = 310. 2) if the solubility of this salt is 8. 1 x 10 -4 g/L. (ans. : 1. 3 x 10 -26) 6/12/2021 Chapter 17 18

Example 3 (4 on Example Problems Handout) The Ksp for Ca. F 2 (FW = 78 g/mol) is 4. 0 x 10 -11. What is the molar solubility of Ca. F 2 in water? What is the solubility of Ca. F 2 in water in g/L? (ans. : 2. 2 x 10 -4 M, 0. 017 g/L) 6/12/2021 Chapter 17 19

Precipitation reaction exchange reaction one product is insoluble Example Overall: Ca. Cl 2(aq) + Na 2 CO 3(aq) --> Ca. CO 3(s) + 2 Na. Cl(aq) 6/12/2021 Chapter 17 20

Precipitation reaction exchange reaction one product is insoluble Example Overall: Ca. Cl 2(aq) + Na 2 CO 3(aq) --> Ca. CO 3(s) + 2 Na. Cl(aq) Na+ and Ca 2+ “exchange” anions 6/12/2021 Chapter 17 21

Precipitation reaction exchange reaction one product is insoluble Example Overall: Ca. Cl 2(aq) + Na 2 CO 3(aq) --> Ca. CO 3(s) + 2 Na. Cl(aq) Net Ionic: Ca 2+(aq) + CO 32 -(aq) <=> Ca. CO 3(s) 6/12/2021 Chapter 17 22

Precipitation Compare precipitation to solubility equilibrium Ca 2+(aq) + CO 32 -(aq) <=> Ca. CO 3(s) prec. vs Ca. CO 3(s) <=> Ca 2+(aq) + CO 32 -(aq) sol. Equil. saturated solution 6/12/2021 Chapter 17 23

Precipitation Compare precipitation to solubility equilibrium: Ca 2+(aq) + CO 32 -(aq) <=> Ca. CO 3(s) vs Ca. CO 3(s) <=> Ca 2+(aq) + CO 32 -(aq) saturated solution Precipitation occurs until solubility equilibrium is established. 6/12/2021 Chapter 17 24

Precipitation Ca 2+(aq) + CO 32 -(aq) <=> Ca. CO 3(s) vs Ca. CO 3(s) <=> Ca 2+(aq) + CO 32 -(aq) saturated solution Key to forming ionic precipitates: Mix ions so concentrations exceed those in saturated solution (supersaturated solution) 6/12/2021 Chapter 17 25

Predicting Precipitation To determine if solution is supersaturated: Compare ion product (Q or IP) to Ksp For Mx. Ay(s) <=> x. My+(aq) + y. Ax-(aq) u. Q = [My+]x[Ax-]y u Q calculated for initial conditions Q > Ksp supersaturated solution, precipitation occurs, solubility equilibrium established (Q = Ksp) = Ksp saturated solution, no precipitation u Q < Ksp unsaturated solution, no precipitation u. Q 6/12/2021 Chapter 17 26

Predicting Precipitation Basic Steps for Predicting Precipitation Consult solubility rules (if necessary) to determine what ionic compound might precipitate Write the solubility equilibrium for this substance Pay close attention to the stoichiometry Calculate the moles of each ion involved before mixing moles = M x L or moles = mass/FW Calculate the concentration of each ion involved after mixing assuming no reaction Calculate Q and compare to Ksp 6/12/2021 Chapter 17 27

Example 4 (7 and 8 on Example Problems Handout) Will a precipitate form if (a) 500. 0 m. L of 0. 0030 M lead nitrate, Pb(NO 3)2, and 800. 0 m. L of 0. 0040 M sodium fluoride, Na. F, are mixed, and (b) 500. 0 m. L of 0. 0030 M Pb(NO 3)2 and 800. 0 m. L of 0. 040 M Na. F are mixed? (ans. : (a) No, Q = 7. 5 x 10 -9; (b) Yes, Q = 7. 5 x 10 -7) 6/12/2021 Chapter 17 28

Solubility of Ionic Compounds Solubility Rules All alkali metal compounds are soluble The nitrates of all metals are soluble in water. Most compounds containing chloride are soluble. The exceptions are those with Ag+, Pb 2+, and Hg 22+ Most compounds containing fluoride are soluble. The exceptions are those with Mg 2+, Ca 2+, Sr 2+, Ba 2+, and Pb 2+ Ex. 4: Possible precipitate = Pb. F 2 (Ksp = 4. 1 x 10 -8) 6/12/2021 Chapter 17 29

Example 5 (10 on Example Problem Handout) A student carefully adds solid silver nitrate, Ag. NO 3, to a 0. 0030 M solution of sodium sulfate, Na 2 SO 4. What [Ag+] in the solution is needed to just initiate precipitation of silver sulfate, Ag 2 SO 4 (Ksp = 1. 4 x 10 -5)? (ans. : 0. 068 M) 6/12/2021 Chapter 17 30

Factors that Affect Solubility Common Ion Effect p. H Complex-Ion Formation 6/12/2021 Chapter 17 32

Factors that Affect Solubility Common Ion Effect p. H Complex-Ion Formation 6/12/2021 Chapter 17 These sure sound familiar. Where have I seen them before? 33

Common Ion Effect and Solubility Consider the solubility equilibrium of Ag. Cl(s) <=> Ag+(aq) + Cl-(aq) How does adding excess Na. Cl affect the solubility equilibrium? Na. Cl(s) Na+(aq) + Cl-(aq) 6/12/2021 Chapter 17 34

Common Ion Effect and Solubility Consider the solubility equilibrium of Ag. Cl(s) <=> Ag+(aq) + Cl-(aq) How does adding excess Na. Cl affect the solubility equilibrium? Na. Cl(s) Na+(aq) + Cl-(aq) 2 sources of Cl. Cl- is common ion 6/12/2021 Chapter 17 35

Example 6 (11 on Example Problem Handout) What is the molar solubility of Ag. Cl (Ksp = 1. 8 x 10 -10) in a 0. 020 M Na. Cl solution? What is the molar solubility of Ag. Cl in pure water? (ans. : 8. 5 x 10 -9, 1. 3 x 10 -5) 6/12/2021 Chapter 17 36

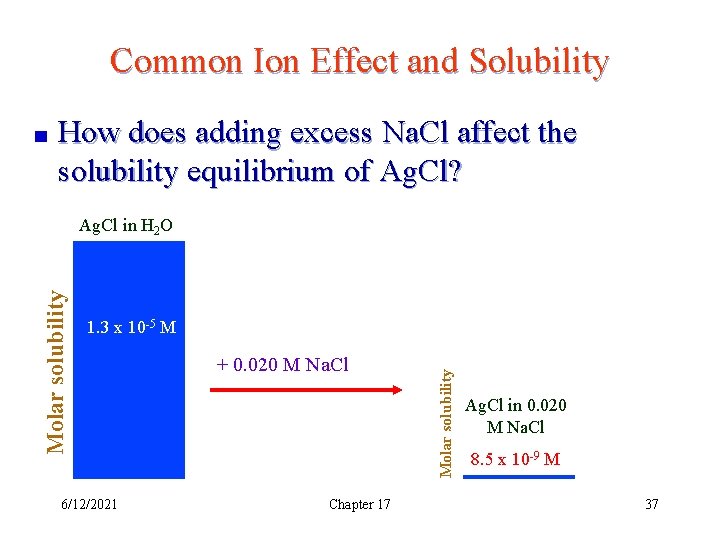
Common Ion Effect and Solubility How does adding excess Na. Cl affect the solubility equilibrium of Ag. Cl? 1. 3 x 10 -5 M 6/12/2021 + 0. 020 M Na. Cl Chapter 17 Molar solubility Ag. Cl in H 2 O Ag. Cl in 0. 020 M Na. Cl 8. 5 x 10 -9 M 37

Common Ion Effect and Solubility Why does the molar solubility of Ag. Cl decrease after adding Na. Cl? Understood in terms of Le. Chatelier’s principle: Na. Cl(s) --> Na+ + Cl- 6/12/2021 Chapter 17 38

Common Ion Effect and Solubility Why does the molar solubility of Ag. Cl decrease after adding Na. Cl? Understood in terms of Le. Chatelier’s principle: Na. Cl(s) --> Na+ + Cl. Ag. Cl(s) <=> Ag+ + Cl- 6/12/2021 Chapter 17 39

Common Ion Effect and Solubility Why does the molar solubility of Ag. Cl decrease after adding Na. Cl? Understood in terms of Le. Chatelier’s principle: Na. Cl(s) --> Na+ + Cl. Ag. Cl(s) <=> Ag+ + Cl. Common-Ion Effect 6/12/2021 Chapter 17 44

p. H and Solubility How can p. H influence solubility? Solubility of “insoluble” salts will be affected by p. H changes if the anion of the salt is at least moderately basic Solubility increases as p. H decreases Solubility decreases as p. H increases 6/12/2021 Chapter 17 45

p. H and Solubility Salts contain either basic or neutral anions: basic anions Strong bases: OH-, O 2 Weak bases (conjugate bases of weak molecular acids): F -, S 2 -, CH COO-, CO 2 -, PO 3 -, C O 2 -, Cr. O 2 -, etc. 3 3 4 2 4 4 Solubility affected by p. H changes neutral anions (conjugate bases of strong monoprotic acids) Cl-, Br-, I-, NO 3 -, Cl. O 4 Solubility not affected by p. H changes 6/12/2021 Chapter 17 46

p. H and Solubility Example: Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 6/12/2021 Chapter 17 47

p. H and Solubility Example: Fe(OH)2 -Add acid Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 6/12/2021 Chapter 17 48

p. H and Solubility Example: Fe(OH)2 -Add acid Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 2 H 3 O+(aq) + 2 OH-(aq) 4 H 2 O 6/12/2021 Chapter 17 49

p. H and Solubility Example: Fe(OH)2 -Add acid Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 2 H 3 O+(aq) + 2 OH-(aq) 4 H 2 O Which way does this reaction shift the solubility equilibrium? Why? Understood in terms of Le. Chatlier’s principle 6/12/2021 Chapter 17 50

p. H and Solubility Example: Fe(OH)2 -Add acid More Fe(OH)2 dissolves in response Solubility increases Decrease = stress Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) Stress relief = increase [OH-] 2 H 3 O+(aq) + 2 OH-(aq) 4 H 2 O 6/12/2021 Chapter 17 51

p. H and Solubility Example: Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 2 H 3 O+(aq) + 2 OH-(aq) 4 H 2 O(l) overall Fe(OH)2(s) + 2 H 3 O+(aq) <=> Fe 2+(aq) + 4 H 2 O(l) 6/12/2021 Chapter 17 52

p. H and Solubility Example: Fe(OH)2(s) <=> Fe 2+(aq) + 2 OH-(aq) 2 H 3 O+(aq) + 2 OH-(aq) 4 H 2 O(l) overall Fe(OH)2(s) + 2 H 3 O+(aq) <=> Fe 2+(aq) + 4 H 2 O(l) decrease p. H increase p. H 6/12/2021 solubility increases solubility decreases Chapter 17 53

p. H, Solubility, and Tooth Decay Enamel (hydroxyapatite) = Ca 10(PO 4)6(OH)2 (insoluble ionic compound) Ca 10(PO 4)6(OH)2 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 OH-(aq) 6/12/2021 Chapter 17 54

p. H, Solubility, and Tooth Decay Enamel (hydroxyapatite) = Ca 10(PO 4)6(OH)2 (insoluble ionic compound) weak base strong base Ca 10(PO 4)6(OH)2 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 OH-(aq) 6/12/2021 Chapter 17 55

p. H, Solubility, and Tooth Decay + food metabolism (Yummy) organic acids (H 3 O+) bacteria in mouth 6/12/2021 Chapter 17 56

p. H, Solubility, and Tooth Decay Ca 10(PO 4)6(OH)2(s) 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 OH-(aq) + H 3 O+(aq) 2 H 2 O(l) PO 43 -(aq) + H 3 O+(aq) HPO 43 -(aq) + H 2 O(l) 6/12/2021 Chapter 17 57

p. H, Solubility, and Tooth Decay Solubility increases Leads to tooth decay Decrease = stress More Ca 10(PO 4)6(OH)2 dissolves in response Decrease = stress Ca 10(PO 4)6(OH)2(s) 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 OH-(aq) + H 3 O+(aq) 2 H 2 O(l) PO 43 -(aq) + H 3 O+(aq) HPO 43 -(aq) + H 2 O(l) 6/12/2021 Chapter 17 58

Tooth Decay 6/12/2021 Chapter 17 59

p. H, Solubility, and Tooth Decay Why fluoridation? F- replaces OH- in enamel Ca 10(PO 4)6(F)2(s) 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 F-(aq) fluorapatite 6/12/2021 Chapter 17 60

p. H, Solubility, and Tooth Decay Why fluoridation? F- replaces OH- in enamel Ca 10(PO 4)6(F)2(s) 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 F-(aq) Less soluble (has lower Ksp) than Ca 10(PO 4)6(OH)2 weaker base than OHmore resistant to acid attack Factors together fight tooth decay! 6/12/2021 Chapter 17 61

p. H, Solubility, and Tooth Decay Why fluoridation? F- replaces OH- in enamel Ca 10(PO 4)6(F)2(s) 10 Ca 2+(aq) + 6 PO 43 -(aq) + 2 F-(aq) F- added to drinking water as Na. F or Na 2 Si. F 6 1 ppm = 1 mg/L F- added to toothpastes as Sn. F 2, Na. F, or Na 2 PO 3 F 0. 1 - 0. 15 % w/w 6/12/2021 Chapter 17 62

Complex Ion Formation and Solubility Metals act as Lewis acids (see Chapter 15) Example Fe 3+(aq) + 6 H 2 O(l) Fe(H 2 O)63+(aq) Lewis acid 6/12/2021 Lewis base Chapter 17 63

Complex Ion Formation and Solubility Metals act as Lewis acids (see Chapter 15) Example Fe 3+(aq) + 6 H 2 O(l) Fe(H 2 O)63+(aq) Complex ion/complex contains central metal ion bonded to one or more molecules or anions called ligands Lewis acid = metal Lewis base = ligand 6/12/2021 Chapter 17 64

Complex Ion Formation and Solubility Metals act as Lewis acids (see Chapter 15) Example Fe 3+(aq) + 6 H 2 O(l) Fe(H 2 O)63+(aq) Complex ions are often water soluble Ligands often bond strongly with metals Kf >> 1: Equilibrium lies very far to right. 6/12/2021 Chapter 17 65

Complex Ion Formation and Solubility Metals act as Lewis acids (see Chapter 15) Other Lewis bases react with metals also Examples Fe 3+(aq) + 6 CN-(aq) Fe(CN)63 -(aq) Lewis acid Lewis base Complex ion Ni 2+(aq) + 6 NH 3(aq) Ni(NH 3)62+(aq) Lewis acid Lewis base Complex ion Ag+(aq) + 2 S 2 O 32 -(aq) Ag(S 2 O 3)23 -(aq) Lewis acid 6/12/2021 Lewis base Chapter 17 Complex ion 66

Complex-Ion Formation and Solubility How does complex ion formation influence solubility? Solubility of “insoluble” salts increases with addition of Lewis bases if the metal ion forms a complex with the base. 6/12/2021 Chapter 17 67

Complex-Ion Formation and Solubility Example Ag. Cl(s) Ag+(aq) + Cl-(aq) 6/12/2021 Chapter 17 68

Complex-Ion Formation and Solubility Example Ag. Cl-Add NH 3 Ag. Cl(s) Ag+(aq) + Cl-(aq) Ag+(aq) + 2 NH 3(aq) Ag(NH 3)2+(aq) 6/12/2021 Chapter 17 69

Complex-Ion Formation and Solubility Example Ag. Cl-Add NH 3 Ag. Cl(s) Ag+(aq) + Cl-(aq) Ag+(aq) + 2 NH 3(aq) Ag(NH 3)2+(aq) Which way does this reaction shift the solubility equilibrium? Why? 6/12/2021 Chapter 17 70

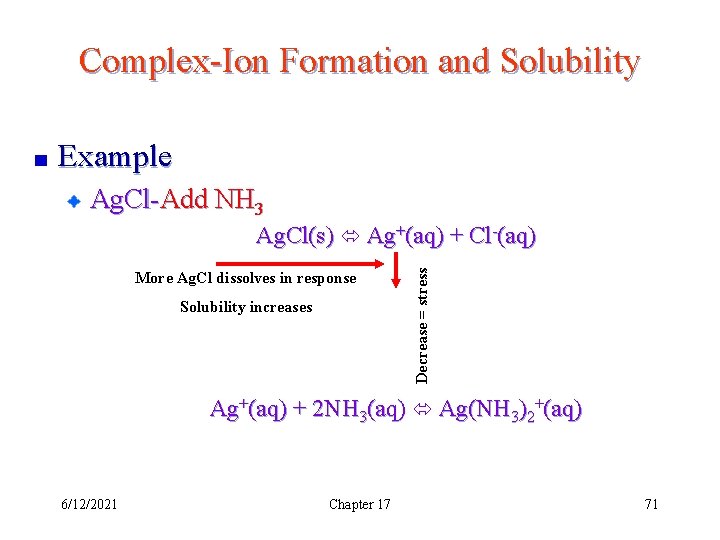
Complex-Ion Formation and Solubility Example Ag. Cl-Add NH 3 More Ag. Cl dissolves in response Solubility increases Decrease = stress Ag. Cl(s) Ag+(aq) + Cl-(aq) Ag+(aq) + 2 NH 3(aq) Ag(NH 3)2+(aq) 6/12/2021 Chapter 17 71

Complex-Ion Formation and Solubility Example Ag. Cl overall Ag. Cl(s) Ag+(aq) + Cl-(aq) Ag+(aq) + 2 NH 3(aq) Ag(NH 3)2+(aq) Ag. Cl(s) + 2 NH 3(aq) Ag(NH 3)2+(aq) + Cl-(aq) Addition of ligand solubility increases 6/12/2021 Chapter 17 72

Summary: Factors that Influence Solubility Common Ion Effect Decreases solubility p. H decreases Increases solubility p. H increases Decreases solubility Salt must have basic anion Complex-Ion Formation Increases solubility 6/12/2021 Chapter 17 73

End of Presentation 6/12/2021 Chapter 17 74