CH 15 CONDITIONAL PROBABILITY AND INDEPENDENCE PART 1

CH 15 CONDITIONAL PROBABILITY AND INDEPENDENCE PART 1 Agenda Objective 1. Review Ch 14 2. Ch 14 Partner Quiz 3. Notes on Ch 15 part 1 • We will review conditional probability, then we will learn how to test for independence, and calculate probabilities for events that draw without replacement.

CONDITIONAL PROBABILITY • The probability that one event happens or that another event happens. • Apply the General Addition Rule P(A U B) = P(A) + P(B) - P(A∩B)

EXAMPLE Police report that 78% of drivers stopped on suspicion of drunk driving are given a breath test, 36% a blood test, and 22% both tests. What is the probability that a randomly selected DWI suspect is given… A test? A blood test or a breath test, but not both? Neither test?

CONDITIONAL PROBABILITY • The probability that one event happens given that another event is already known. • Apply the General Multiplication Rule P(A∩B) = P(A) ∙ P(B│A) … • Without replacement.

EXAMPLE. . MRS. KENNEDY HAS A BAG OF STARBURSTS. THERE ARE 10 RED, 12 ORANGE, 8 YELLOW, AND 6 PINK. Scenario 1: Your favorite flavor is pink, what is the probability the you draw a pink? Scenario 2: Two people get to draw before you, one draws an orange the other draws a pink. What are your chances now of drawing a pink?

EXAMPLE: STANDARD DECK OF CARDS Scenario 1: What is the probability of drawing three face cards in a row, with replacement? Scenario 2: What is the probability of drawing three face cards in a row, WITHOUT replacement?


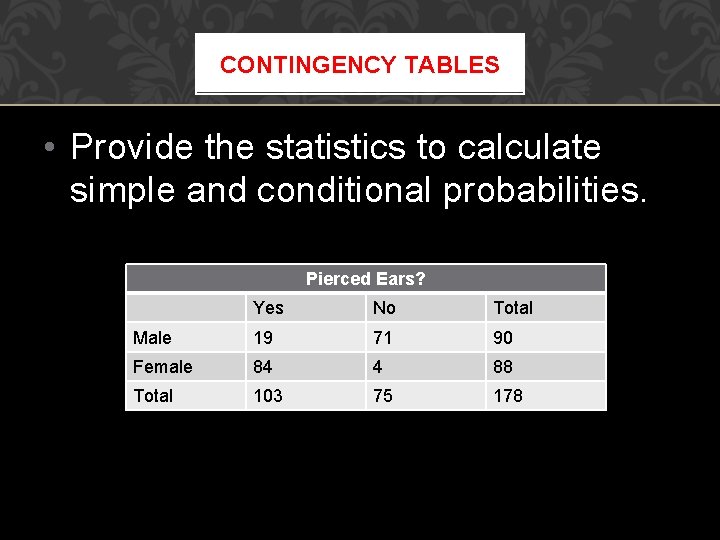
CONTINGENCY TABLES • Provide the statistics to calculate simple and conditional probabilities. Pierced Ears? Yes No Total Male 19 71 90 Female 84 4 88 Total 103 75 178

Pierced Ears? Male Yes No CONTINGENCY TABLES Total 19 71 90 Female 84 4 88 Total 103 75 178 1. What is the probability that a student picked at random is male? 2. What is the probability that a student picked at random is pierced? 3. What is the probability that a student picked at random is a pierced male? 4. What is the probability that a student picked at random is pierced or male?

Pierced Ears? Male Yes No CONTINGENCY TABLES Total 19 71 90 Female 84 4 88 Total 103 75 178 1. What is the probability that a student is male given the student is pierced? 2. What is the probability that a student picked at random is pierced given he is male? 3. What is the probability that a student picked at random is a pierced given the student is female? 4. What is the probability that a student picked at random is female given she is pierced?

CONDITIONAL PROBABILITY

Pierced Ears? CONTINGENCY Yes No TABLES Total Male 19 71 90 Female 84 4 88 Total 103 75 178 What is the probability that a student is male given he is pierced? What is the probability that a student is pierced given the student is female?

Grade Level School A B CONTINGENCY TABLES Below B Liberal Arts 2142 1890 2268 Engineering 368 423 800 Health 882 630 588 1. What is the probability that a student received below a B? 2. What is the probability that a student is in engineering given he has below a B? 3. What is the probability that a student picked at random has lower than a B, given he is in engineering? 4. Which of these conditional probabilities tells you whether this college’s Engineering students tend to earn low grades than liberal arts or Health?

INDEPENDENCE? ? • IF P(A∩B) = P(A) X P(B) when independent and …. . • P(A∩B) = P(B) X P(B│A) as a general rule. • By substitution…. • P(B│A) = P(B) independence. confirms

INDEPENDENCE? ?
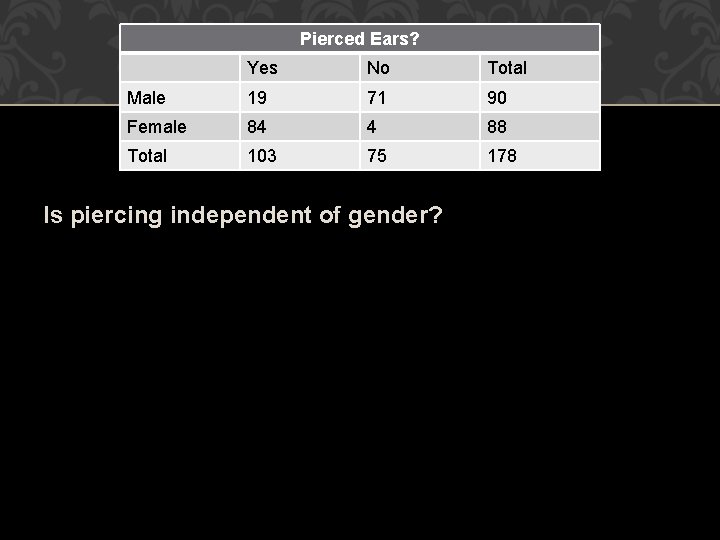
Pierced Ears? CONTINGENCY Yes No TABLES Total Male 19 71 90 Female 84 4 88 Total 103 75 178 Is piercing independent of gender?

GENERAL ADDITION RULE P(A U B) = P(A) + P(B) – P(A ∩ B)

GENERAL ADDITION RULE Example: Police report that 78% of drivers stopped on suspicion of drunk driving are given a breath test, 36% a blood test, and 22% both tests. What is the probability that a randomly selected DWI suspect is given…. a) A test? b) A blood test or a breath test, but not both? c) Neither test?

GENERAL ADDITION RULE Example: Suppose the probability that a U. S. resident has traveled to Canada is 0. 18, to Mexico is 0. 09, and to both countries is 0. 04. What’s the probability that an American chosen at random has…. a) Traveled to Canada but not Mexico? b) Traveled to either Canada or Mexico? c) Not traveled to either country?

INDEPENDENT VS. DISJOINT • Disjoint events do • Independent not share any events are events in occurrences, which the occurrence therefore there is no of one event does not intersection of events. affect the other. • Use Addition Rule • Use Multiplication Rule • OR P(A U B) • AND P(A ∩ B) • P(A) + P(B) • P(A) X P(B)

DISJOINT OR INDEPENDENT? • What is the probability a card drawn is an ace or red?

DISJOINT OR INDEPENDENT? • Two cards are drawn without replacement. What is the probability they are both aces?

DISJOINT OR INDEPENDENT? • Are a “red card” and “spade independent or mutually exclusive?

DISJOINT OR INDEPENDENT? • Are “red card” and “ace” independent? Mutually exclusive?

DISJOINT OR INDEPENDENT? • Are “face card” and “king” independent? Mutually exclusive?

INDEPENDENCE? ? Jeans Other Total Male 12 5 17 Female 8 11 19 Total 20 16 36 What is the probability that a male wears jeans?

INDEPENDENCE? ? Jeans Other Total Male 12 5 17 Female 8 11 19 Total 20 16 36 What is the probability that someone wearing jeans is a m

INDEPENDENCE? ? Jeans Other Total Male 12 5 17 Female 8 11 19 Total 20 16 36 Are being male and wearing jeans disjoint? Are sex and attire independent?
- Slides: 29