Ch 13 Sequential Data Pattern Recognition and Machine
















- Slides: 18

Ch 13. Sequential Data Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Summarized by B. -W. Ku Biointelligence Laboratory, Seoul National University http: //bi. snu. ac. kr/ 1

Contents l 13. 3. Linear Dynamical Systems ¨ 13. 3. 1 Inference in LDS ¨ 13. 3. 2 Learning in LDS ¨ 13. 3. 3 Extensions of LDS ¨ 13. 3. 4 Particle filters (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 2

A Stochastic Linear Dynamical System Fig. 13. 15 (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 3

13. 3. 1 Inference in LDS (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 4

Inference Problem l Finding the marginal distributions for the latent variables conditional on the observation sequence. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 5

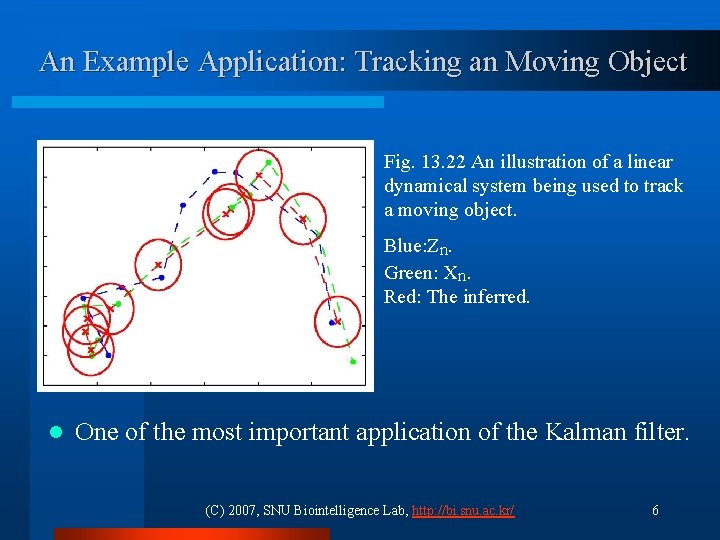
An Example Application: Tracking an Moving Object Fig. 13. 22 An illustration of a linear dynamical system being used to track a moving object. Blue: Zn. Green: Xn. Red: The inferred. l One of the most important application of the Kalman filter. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 6

Mean and Variance of p(zn|x 1, …, xn) l Kalman filter equations (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 7

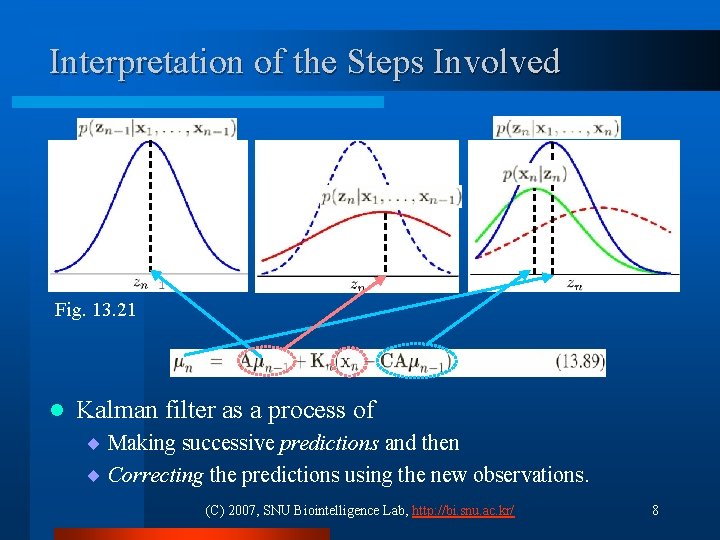
Interpretation of the Steps Involved Fig. 13. 21 l Kalman filter as a process of ¨ Making successive predictions and then ¨ Correcting the predictions using the new observations. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 8

Derivation of Eq. 13. 89, 13. 90, 13. 94, 13. 95 (13. 85), (13. 59) forward recursion (13. 84) (13. 87) (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 9

Mean and Variance of p(zn|x 1, …, xn+1, …, x. N) (13. 84) l Kalman smoother equations. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 10

Derivation of Eq. 13. 100, 13. 101 (13. 62) backward recursion the forward-backward algorithm (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 11

13. 3. 2 Learning in LDS (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 12

Learning Problem l Determining the parameters θ = {A, Γ, C, Σ, μ 0, V 0} using the EM algorithm. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 13

Expectation of Log Likelihood Function l The complete data ({X, Z}) log likelihood function (13. 108) l The expectation of the log likelihood function with respect to p(Z | X, θ old) (13. 109) (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 14

Maximizing the Expectation l Maximizing each term with respect to the parameters. (Section 2. 3. 4) (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 15

Evaluated θ new (13. 105) (13. 106) (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ (13. 107) 16

13. 3. 3 Extensions of LDS l Problem: Beyond the linear-Gaussian assumption. ¨ Considerable interest in extending the basic linear dynamical system in order to increase its capabilities. ¨ Gaussian p(zn |xn) – A significant limitation. l Some extensions ¨ Gaussian mixture p(zn). ¨ Gaussian mixture p(xn |zn) – Impractical. ¨ The extended Kalman filter. ¨ The switching state space model / the switching hidden Markov model. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 17

13. 3. 4 Particle filters l Non-Gaussian emission density p(xn |zn) non-Gaussian p(zn | x 1, …, xn) mathematically intractable integral l Sampling-importanceresampling Fig. 13. 21 A schematic illustration of the operation of particle filter. (C) 2007, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 18