CH 13 Kernel Machines A Support Vector Machine



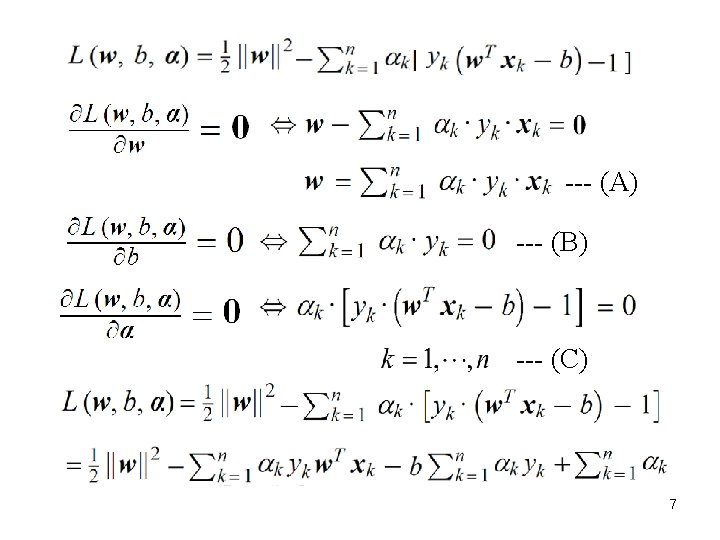
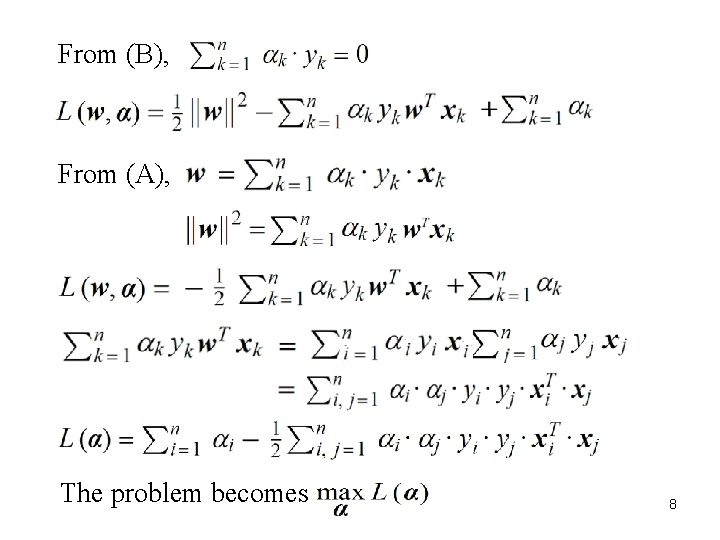











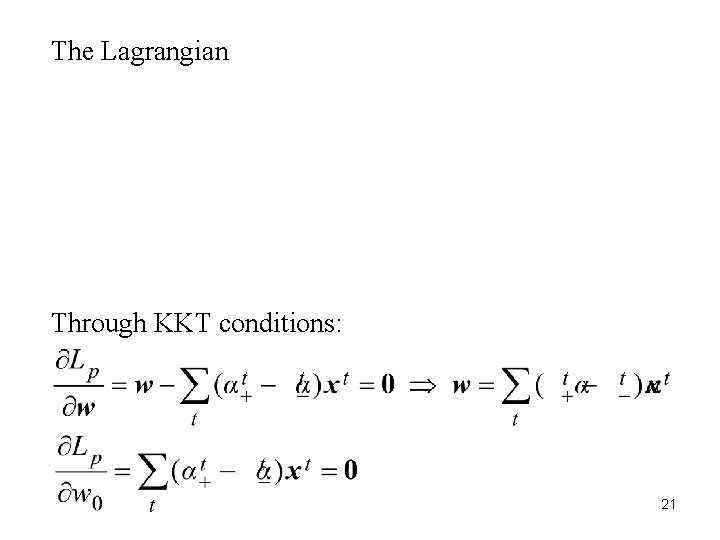
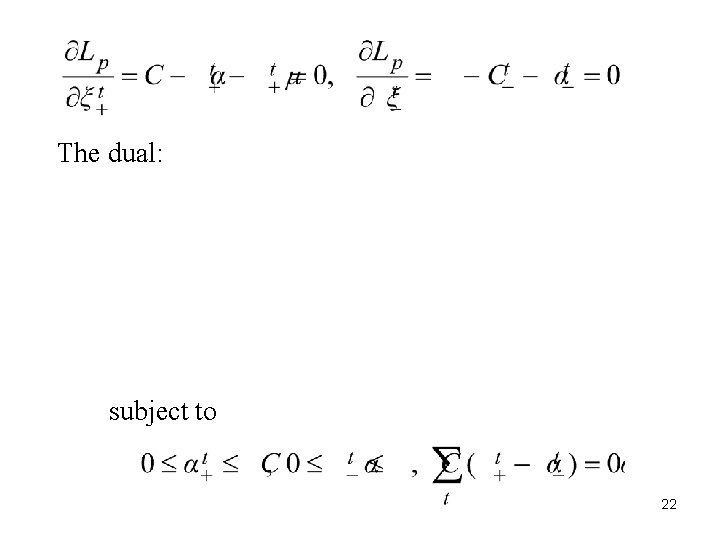


- Slides: 24

CH. 13: Kernel Machines (A) Support Vector Machine (SVM) -- classifier, forward neural network, supervised learning Difficulties with SVM: i) binary classifier, ii) linearly separable patterns 1

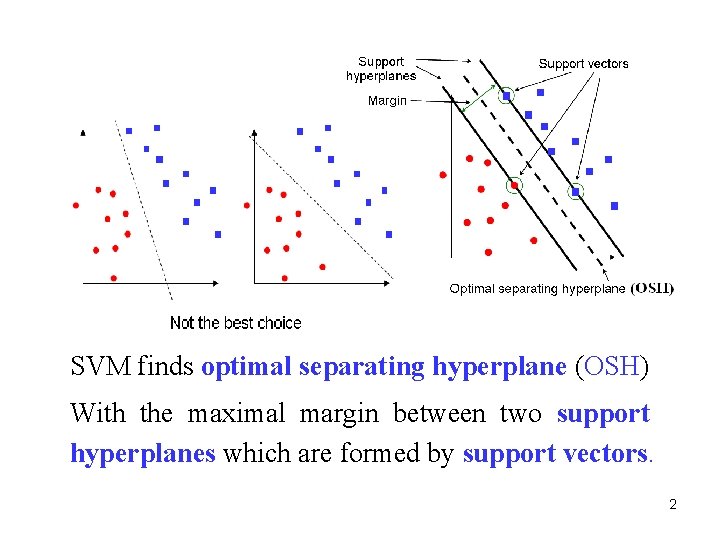
SVM finds optimal separating hyperplane (OSH) With the maximal margin between two support hyperplanes which are formed by support vectors. 2

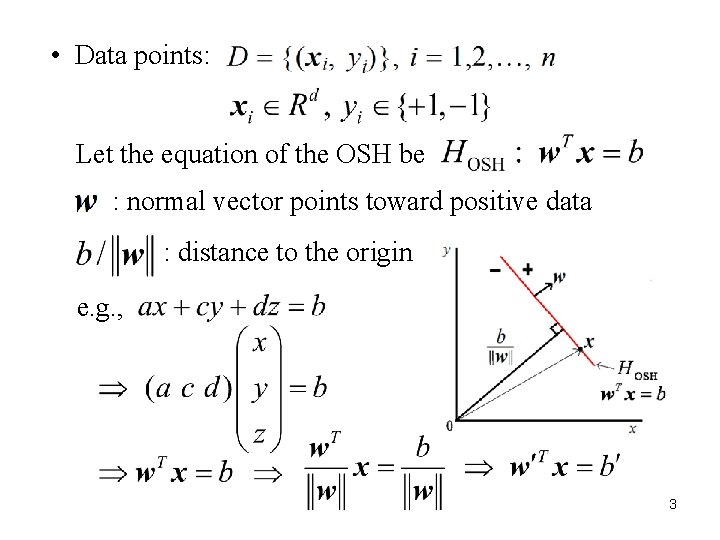
• Data points: Let the equation of the OSH be : normal vector points toward positive data : distance to the origin e. g. , 3

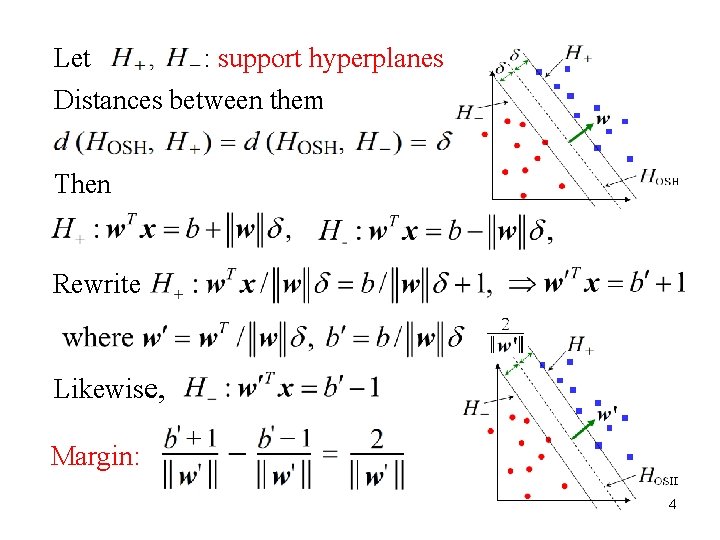
Let : support hyperplanes Distances between them Then Rewrite Likewise, Margin: 4

Replace Maximizing margin Minimizing subject to ( ) satisfying are called support vectors Lagrange Multiplier Method – converts a constrained to an unconstrained problem. 5

The objective function: The optimal solution is given by the saddle point of , which is minimized w. r. t. w and b, while maximized w. r. t. i. e. , . Through Karush–Kuhn–Tucker (KKT) conditions, L defined in the primal space of w, b, is translated to the dual space of 6
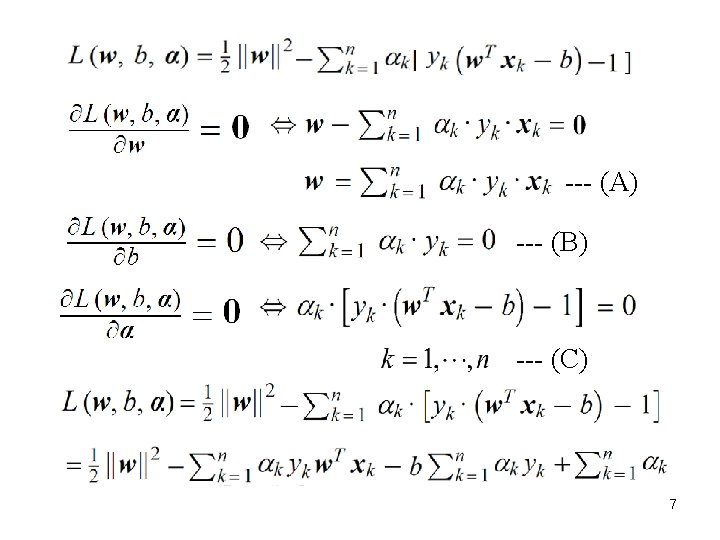
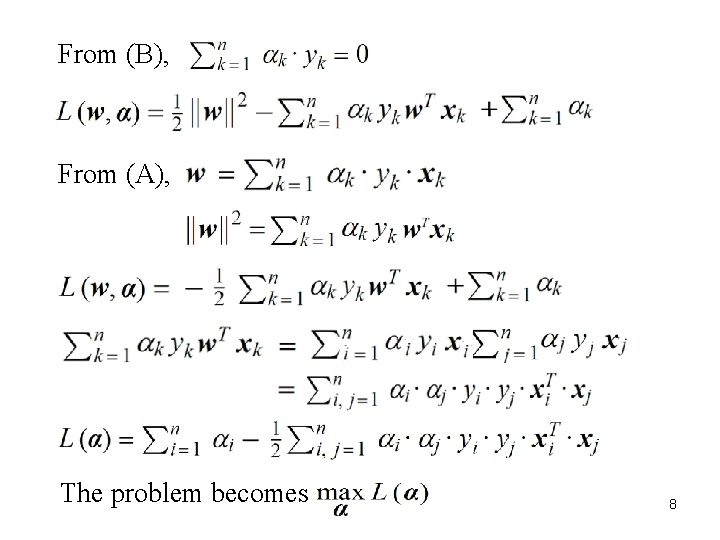
From (B), From (A), The problem becomes 8

After solving by letting find w by (A) . For non-support vectors, From (C), Support vectors are those whose Determine b using any support vector. Consider any support vector : # support vectors 9

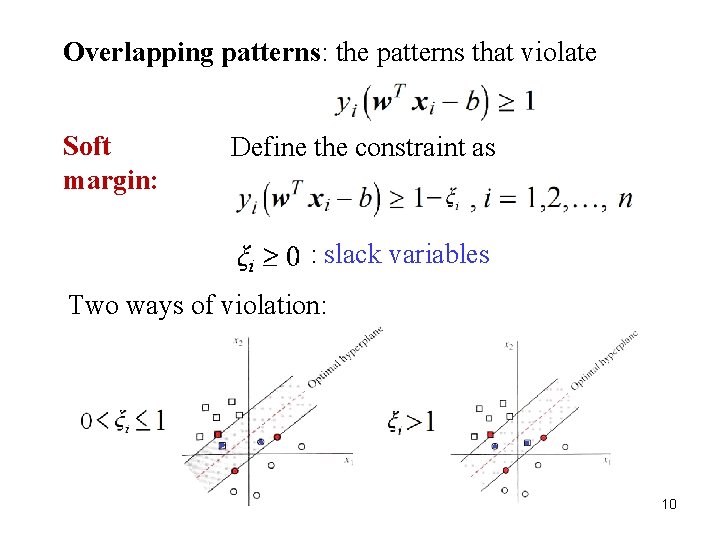
Overlapping patterns: the patterns that violate Soft margin: Define the constraint as : slack variables Two ways of violation: 10

Problem: Find a separating hyperplane for which (i) minimal (ii) (iii) minimal (soft error) Lagrange objective function in the primal space, C: penalty factor 11

Through KKT conditions, Dual space: the space of subject to Different from the separable case in that 12

(B) Kernel Machines 13. 5 Kernel Trick Cover’s theorem: Make nonlinearly separable data linearly separable by mapping them from low to high dimensional space e. g. , 2 D 3 D x : a vector in the original N-D space 13

: a set of functions that transform x to a space of infinite dimensionality. Let The OSH in the new space where 14

Substitute (2), (3) into (1), Let : kernel function 15

A kernel function can be considered as a a measure of similarity between data points. • Mercer conditions: requirements of a kernel function 1. Symmetric 2. 3. 4. 16

13. 6 Examples of Kernel Functions i) Linear kernel: ii) Polynomial kernel with degree d : e. g. , d = 2 17

iii) Perceptron kernel: iv) Sigmoidal kernel: v) Radial basis function kernel: 13. 8 Multiple Kernel Learning A new kernel can be constructed by combining simpler kernels, e. g. , 18

13. 9 Multiclass Kernel Machines (K > 2 classes) 1. Train K 2 -classifiers , each one distinguishing one class from all other classes combined. During testing, 2. Train K(K-1)/2 pairwise classifiers 3. Train a single multiclassifier 19

13. 10 Kernel Machines for Regression • Consider a linear model Define constraints: : slack variables Problem: subject to constraints 20
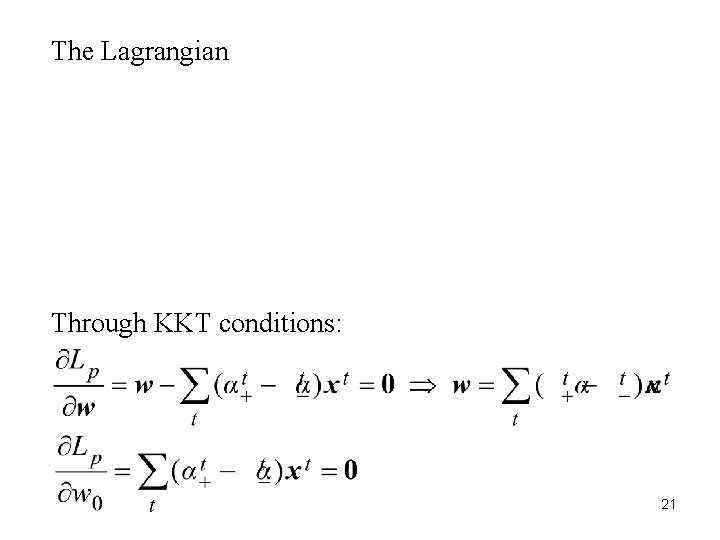
The Lagrangian Through KKT conditions: 21
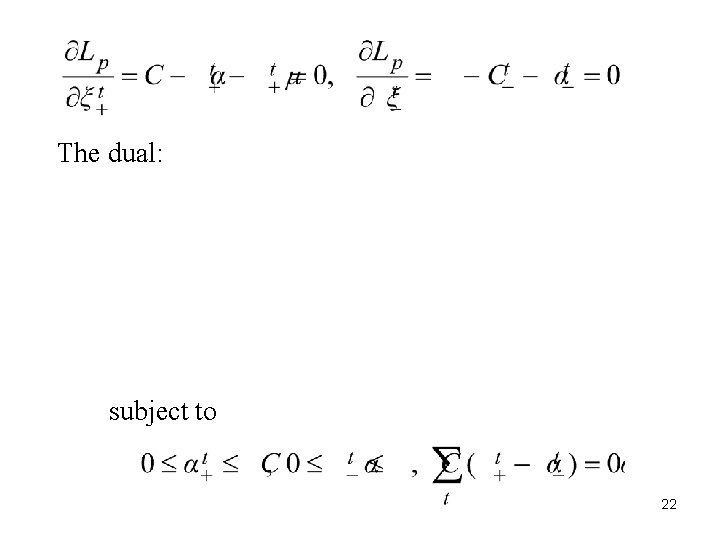
The dual: subject to 22

(a) The examples that fall in the tube have (b) The support vectors satisfy 23

The fitted line kernel function 24