Ch 13 Backtracking BranchandBound There are two principal

Ch 13 – Backtracking + Branch-and-Bound There are two principal approaches to tackling NP-hard problems or other “intractable” problems: • Use a strategy that guarantees solving the problem exactly but doesn’t guarantee to find a solution in polynomial time • Use an approximation algorithm that can find an approximate (sub-optimal) solution in polynomial time 1

Exact solutions The exact solution approach includes: • exhaustive search (brute force) – useful only for small instances • backtracking – eliminates some cases from consideration • branch-and-bound – further cuts down on the search – fast solutions for most instances – worst case is still exponential 2

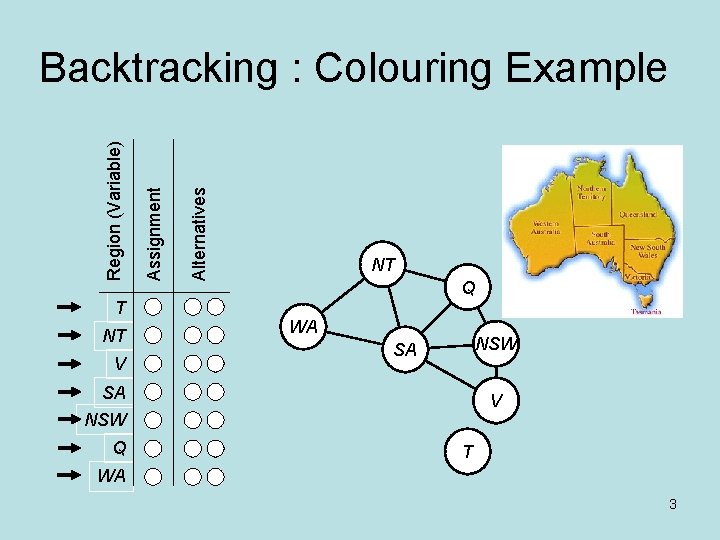
T NT V Alternatives Assignment Region (Variable) Backtracking : Colouring Example NT Q WA NSW SA SA V NSW Q T WA 3

Backtracking • Construct the state space tree: – nodes: partial solutions – edges: choices in completing solutions • Explore the state space tree using depth-first search • “Prune” non-promising nodes – DFS stops exploring subtree rooted at nodes leading to no solutions and. . . – “backtracks” to its parent node 4

Example: n-Queen problem • Place n queens on an n by n chess board so that no two of them are on the same row, column, or diagonal 5

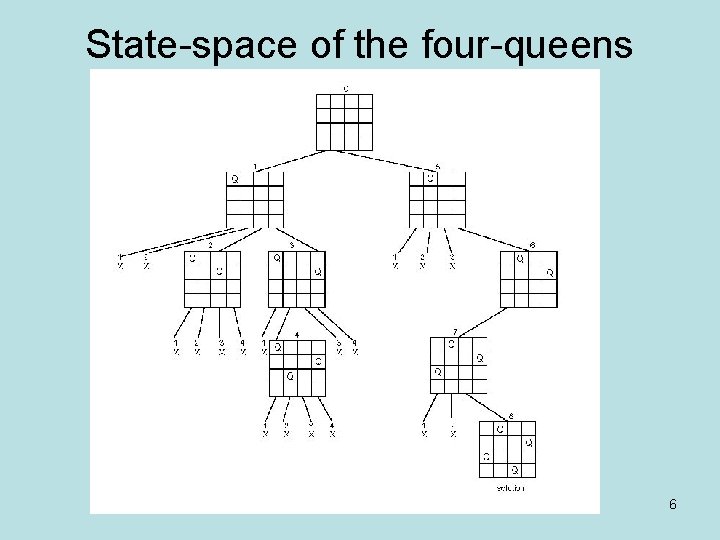
State-space of the four-queens problem 6

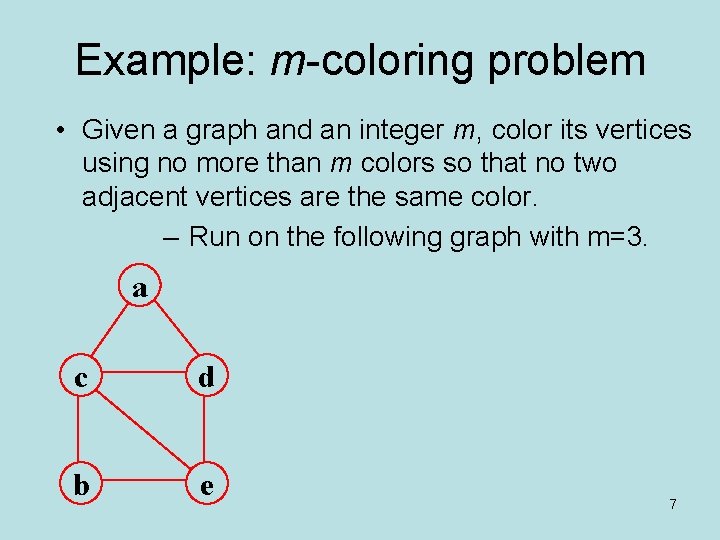
Example: m-coloring problem • Given a graph and an integer m, color its vertices using no more than m colors so that no two adjacent vertices are the same color. – Run on the following graph with m=3. a c d b e 7

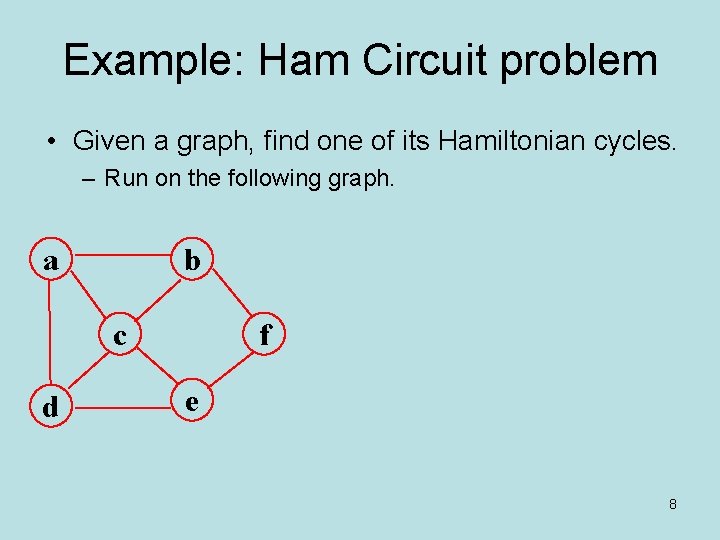
Example: Ham Circuit problem • Given a graph, find one of its Hamiltonian cycles. – Run on the following graph. a b c d f e 8

Example: Subset-Sum problem • Find a subset of a given set S = {s 1, s 2, …, sn} whose sum is equal to a given integer d. – Run on S = {3, 5, 6, 7} and d =15. 9

Branch and Bound • An enhancement of backtracking • Applicable to optimization problems • Uses a lower/upper bound for the value of the objective function for each node (partial solution) so as to: – guide the search through state-space – rule out certain branches as “unpromising” • Lower bound for minimization problems • Upper bound for maximization problems 10

Example: The job-employee assignment problem Select 1 element in each row of the cost matrix C : • no 2 selected elements are in the same col; • and the sum is minimized For example: Job 1 Job 2 Job 3 Job 4 Person a 9 2 7 8 Person b 6 4 3 7 Person c 5 8 1 8 Person d 7 6 9 4 Lower bound: Any solution to this problem will have total cost of at least: 2 + 3 + 1 + 4 = 10. 11

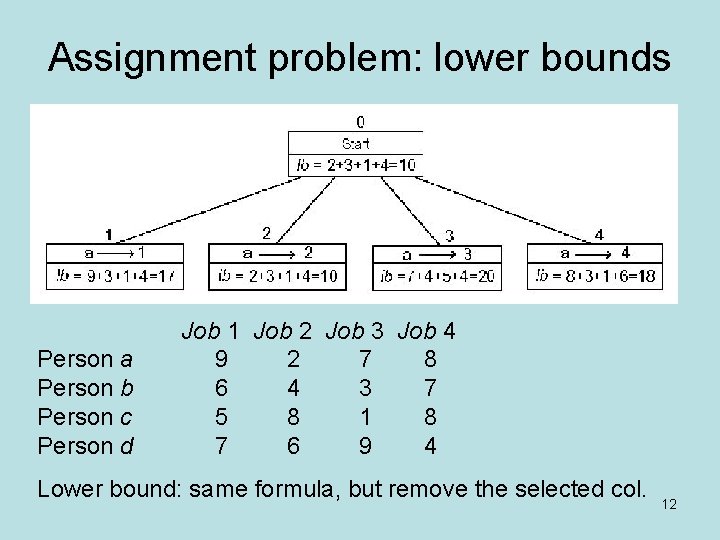
Assignment problem: lower bounds Person a Person b Person c Person d Job 1 Job 2 Job 3 Job 4 9 2 7 8 6 4 3 7 5 8 1 8 7 6 9 4 Lower bound: same formula, but remove the selected col. 12

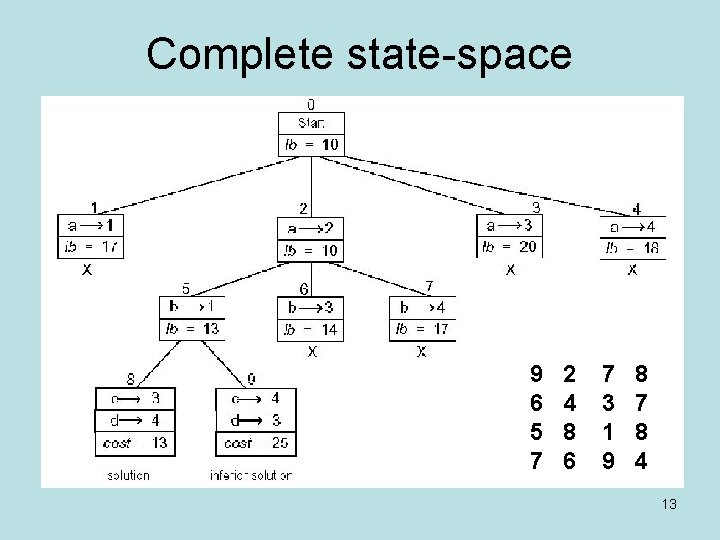
Complete state-space 9 6 5 7 2 4 8 6 7 3 1 9 8 7 8 4 13

Knapsack problem • Run BB algorithm on the following data: – W = 10 (max weight) – Elements (weight, benefit): (4, 40), (7, 42), (5, 25), (3, 12) • Upper bound is calculated as – ub = v + (W-w)(vi+1/wi+1) • v = value of already selected items • w = weight of already selected items 14

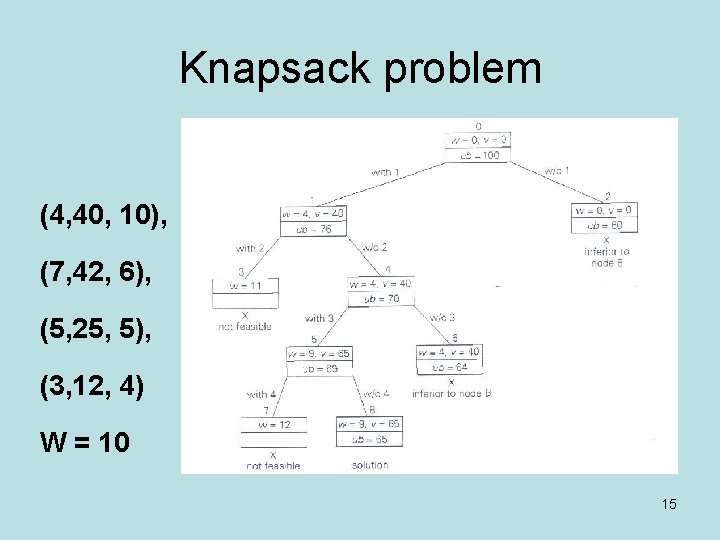
Knapsack problem (4, 40, 10), (7, 42, 6), (5, 25, 5), (3, 12, 4) W = 10 15

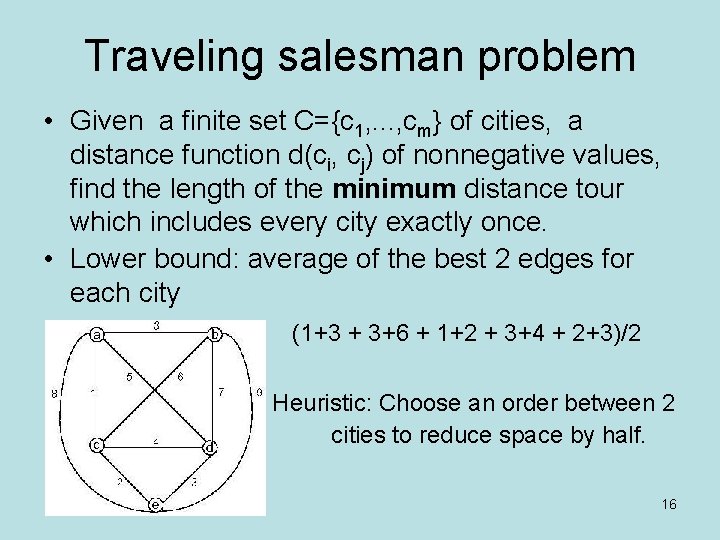
Traveling salesman problem • Given a finite set C={c 1, . . . , cm} of cities, a distance function d(ci, cj) of nonnegative values, find the length of the minimum distance tour which includes every city exactly once. • Lower bound: average of the best 2 edges for each city (1+3 + 3+6 + 1+2 + 3+4 + 2+3)/2 Heuristic: Choose an order between 2 cities to reduce space by half. 16

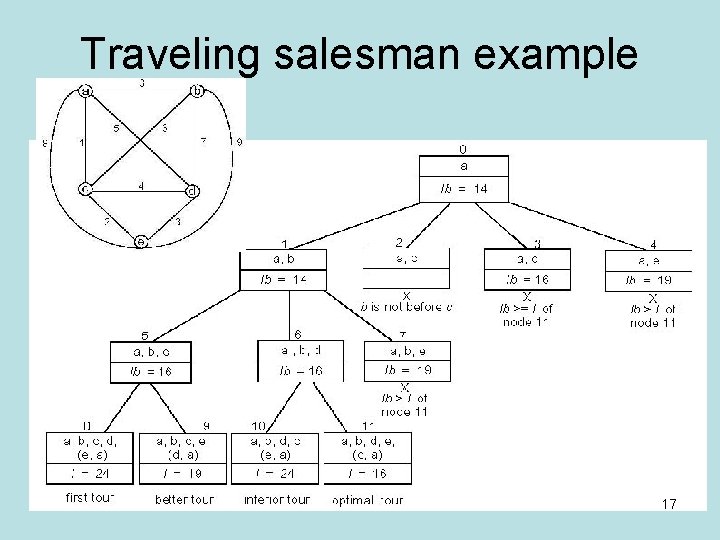
Traveling salesman example 17

Summary • Backtracking consists of doing a DFS of the state space tree, checking whether each node is promising and if the node is nonpromising backtracking to the its parent. • Branch and Bound employs lower bounds for minimization problems, and upper bounds for maximization problems. • It prunes branches that will lead to inferior solutions (than the ones already found). 18