Ch 12 Numerical Solutions to Partial Differential Equations

Ch 12. Numerical Solutions to Partial Differential Equations Applied mathematics. Korea University. Department of Mathematics

Index Ch 12. 1 Elliptic Partial Differential Equations Ch 12. 2 Parabolic Partial Differential Equations Ch 12. 3 Hyperbolic Partial Differential Equations Ch 12. 4 An Introduction to the Finite-Element Mothod Department of Mathematics

§ Elliptic Partial Differential Equations : poisson equation § Parabolic Partial Differential Equations : Heat, diffusion equation § Hyperbolic Partial Differential Equations : wave equation Department of Mathematics

Ch 12. 1 Elliptic Partial Differential Eqeations § Poisson equation Department of Mathematics

Using Taylor series in the variable about Department of Mathematics

Poisson equation at the points Boundary condition Department of Mathematics

Finite – Difference method with truncation error of order Boundary condition Department of Mathematics

Department of Mathematics

Ch 12. 2 Parabolic Partial Differential Eqeations § Parabolic partial differential equation : boundary condition : initial condition Department of Mathematics

Using Taylor series in Department of Mathematics

: local truncation error initial condition boundary condition Department of Mathematics

let : initial condition : Forward Difference method Department of Mathematics

If is made in representing the initial data At n-th time step the error in is . The method is stable The Forward Difference method is therefore stable only if Department of Mathematics

: eigenvalues of A or The Forward Difference method is conditionally stable with rate of convergence Department of Mathematics

To obtain a method that is unconditionally stable : Backward-Difference method where Department of Mathematics

The matrix representation Department of Mathematics

: eigenvalues of A At n-th time step the error in is . The Backward-Difference method is unconditionally stable method. The local truncation error for method is of order. Richardson’s method Department of Mathematics

Crank-Nicolson method : Forward-Difference method at j-th step in : local truncation error : Backward-Difference method at (j+1)th step in : local truncation error Assume that average – difference method Department of Mathematics

The matrix representation where Department of Mathematics

Ch 12. 3 Hyperbolic Partial Differential Eqeations § Hyperbolic partial differential equation Department of Mathematics

Using centered-difference quotient Department of Mathematics

Department of Mathematics

Department of Mathematics

Department of Mathematics

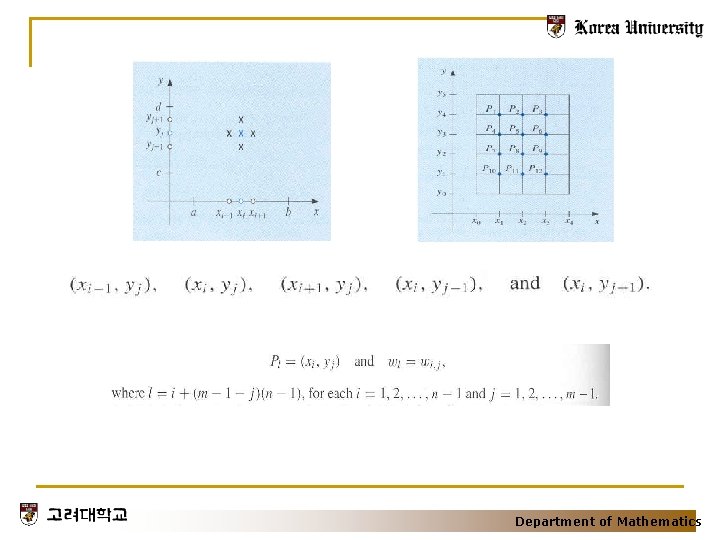
Ch 12. 4 An Introduction to Finite- Element Method boundary condition Department of Mathematics

Polynomials of linear type in and Department of Mathematics

Department of Mathematics

Department of Mathematics

linear system Department of Mathematics

Department of Mathematics

Department of Mathematics

Department of Mathematics