Ch 10 NPcompleteness Tractable and intractable problems DecisionOptimization

Ch 10 - NP-completeness • • • Tractable and intractable problems Decision/Optimization problems Deterministic/Non. Deterministic algorithms Classes P and NP Polynomial reductions NP-complete problems – Cook-Levin theorem – CLIQUE (via SAT CLIQUE reduction) – TSP (via HC TSP reduction) 1

Classifying problems • Classify problems as tractable or intractable. • Problem is tractable if there exists at least one polynomial bound algorithm to solve it. • An algorithm is polynomial bound if its worst case growth rate can be bound by a polynomial p(n) in the size n of the problem 2

Intractable problems • Problem is intractable if it is not tractable. • All algorithms that solve such a problem are not polynomial bound. • It has a worst case growth rate f(n) which cannot be bound by a polynomial p(n) in the size n of the problem. • For intractable problems the bounds are: 3

Why is this classification useful? • If problem is intractable, no point in trying to find an efficient algorithm • All algorithms will be too slow for large inputs. 4

Hard practical problems • There are many practical problems for which no one has yet found a polynomial bound algorithm. • Examples: traveling salesperson, 0/1 knapsack, graph coloring, bin packing etc. • Most design automation problems such as testing and routing. • Many networks, database and graph problems. 5

The theory of NP completeness • The theory of NP-completeness enables showing that these problems are at least as hard as NP-complete problems • Practical implication of knowing problem is NP-complete is that it is probably intractable ( whether it is or not has not been proved yet) • So any algorithm that solves it will probably be very slow for large inputs 6

Decision Problems vs. Optimization Problems • Decision Problem: Yes/no answer • Optimization Problem: Maximization or minimization of a certain quantity • When studying NP-Completeness, it is easier to deal with decision problems than optimization problems 7

Element Uniqueness Problem • Decision Problem: Element Uniqueness – Input: A sequence of integers S – Question: Are there two elements in S that are equal? • Optimization Problem: Element Count – Input: A sequence of integers S – Output: An element in S of highest frequency • What is the algorithm to solve this problem? How much does it cost? 8

Coloring a Graph • Decision Problem: Coloring – Input: G=(V, E) undirected graph and k , k > 0. – Question: Is G k-colorable? • Optimization Problem: Chromatic Number – Input: G=(V, E) undirected graph – Output: The chromatic number of G, (G) • i. e. the minimum number (G) of colors needed to color a graph in such a way that no two adjacent vertices have the same color. 9

Traveling Salesman • Given a finite set C={c 1, . . . , cm} of cities, a distance function d(ci, cj) of nonnegative numbers and a bound B • Decision Problem – Is there a tour of all the cities (in which each city is visited exactly once) with total length at most B? • Optimization Problem – Find the length of the minimum distance tour which includes every city exactly once 10

Cliques • Definition: A clique of size k in G, for some +ve integer k, is a complete subgraph of G with k vertices. • Decision Problem – Input: – Question: • Optimization Problem – Input: – Output: 11

The relation between • If we have a solution to the optimization problem we can compare the solution to the bound answer “yes” or “no”. • Therefore if the optimization problem is tractable so is the decision problem • If the decision problem is “hard” the optimization problem is also “hard” – If the optimization was easy then the decision problem is easy. 12

Deterministic Algorithms • Definition: Let A be an algorithm to solve problem . A is called deterministic if, when presented with an instance of the problem , it has only one choice in each step throughout its execution. – If we run A again and again, is there a possibility that the output may change? • What type of algorithms did we have so far? 13

The Class P • Definition: The class of decision problems P consists of those whose yes/no solution can be obtained using a deterministic algorithm that runs in polynomial time of steps, i. e. O(nk), where k is a non-negative integer and n is the input size. 14

Examples • Sorting: Given n integers, are they sorted in non-decreasing order? • Set Disjointness: Given two sets of integers, are they disjoint? • Shortest path: • 2 -coloring: – Theorem: A graph G is 2 -colorable if and only if G is bipartite if and only if G has no odd length cycle 15

Non-Deterministic Algorithms • A non-deterministic algorithm A on input x consists of two phases: – Guessing: An arbitrary “string of characters y” is (called certificate) generated. • It may or may not correspond to a solution • Not be in proper format of a solution • Differ from one run to another – Verification: A deterministic algorithm verifies • The generated “string of characters y” is a solution 16

Non-Deterministic Algorithms • Definition: Let A be a nondeterministic algorithm for a problem . We say that A accepts an instance I of if and only if on input I, there exists a guess that leads to a yes answer. – Does it mean that if an algorithm A on a given input I leads to an answer of no for a certain guess, that it does not accept it? 17

The Class NP • Definition: The class of decision problems NP consists of those decision problems for which there exists a nondeterministic algorithm that runs in polynomial time. – The running time of a nondeterministic algorithm, is the sum of the running times of the guessing and verification phases. – Both phases need run in polynomial time. – In particular, the verification phase. 18

Example - TSP • Show that the traveling salesman problem belongs to the class of NP problems • Given a problem instance x for TSP and a certificate y – Check that y is indeed a cycle that includes every vertex exactly once – Verify that the length of the cycle is at most B • Is the verification algorithm polynomial? 19

P and NP Problems • What is the difference between P problems and NP Problems? • We can solve problems in P using deterministic algorithms that run in polynomial time • We can check or verify the solution of NP problems in polynomial time using a deterministic algorithm • What is the set relationship between the classes P and NP? 20

Summary: P and NP • Summary so far: – P = problems that can be solved in poly time – NP = problems for which a solution can be verified in polynomial time – P NP – Unknown whether P = NP (most suspect not) • We’ve seen problems that belong to NP that may not belong to P – Hamiltonian path/cycle, TSP problems are in NP – Cannot solve in polynomial time – Easy to verify solution in polynomial time 21

NP-Complete Problems • We will see that NP-Complete problems are the “hardest” problems in NP: – If any one NP-Complete problem can be solved in polynomial time… – …then every NP-Complete problem can be solved in polynomial time… – …and in fact every problem in NP can be solved in polynomial time (showing P = NP) – Thus: solve hamiltonian-cycle in O(n 100) time, you’ve proved that P = NP. Retire rich & famous. 22

Reduction • The crux of NP-Completeness is reducibility – Informally, a problem A can be reduced to another problem B if any instance of A can be “easily rephrased” as an instance of B , the solution to which provides a solution to the instance of A • This rephrasing is called transformation – Intuitively: If A reduces to B, A is “no harder to solve” than B • Total cost: cost of transformation + cost to solve B 23

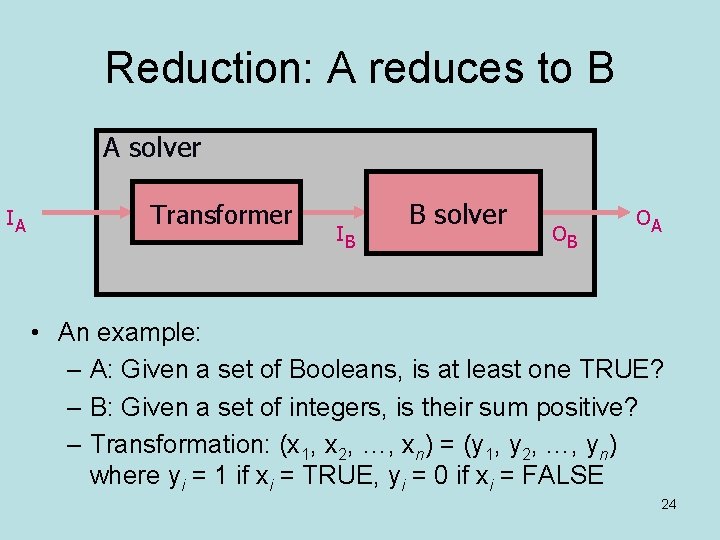
Reduction: A reduces to B A solver IA Transformer IB B solver OB OA • An example: – A: Given a set of Booleans, is at least one TRUE? – B: Given a set of integers, is their sum positive? – Transformation: (x 1, x 2, …, xn) = (y 1, y 2, …, yn) where yi = 1 if xi = TRUE, yi = 0 if xi = FALSE 24

NP-Hard and NP-Complete • If A is polynomial-time reducible to B, we denote this A p B • Definition of NP-Hard and NP-Complete: – If all problems X NP are reducible to A, then A is NP-Hard – We say A is NP-Complete if A is NP-Hard and A NP • If A p B and A is NP-Complete, B is also NP-Complete 25

Why Prove NP-Completeness? • Though nobody has proven that P ≠ NP, if you prove a problem NP-Complete, most people accept that it is probably intractable • Therefore it can be important to prove that a problem is NP-Complete – Don’t need to come up with an efficient algorithm – Can instead work on approximation algorithms 26

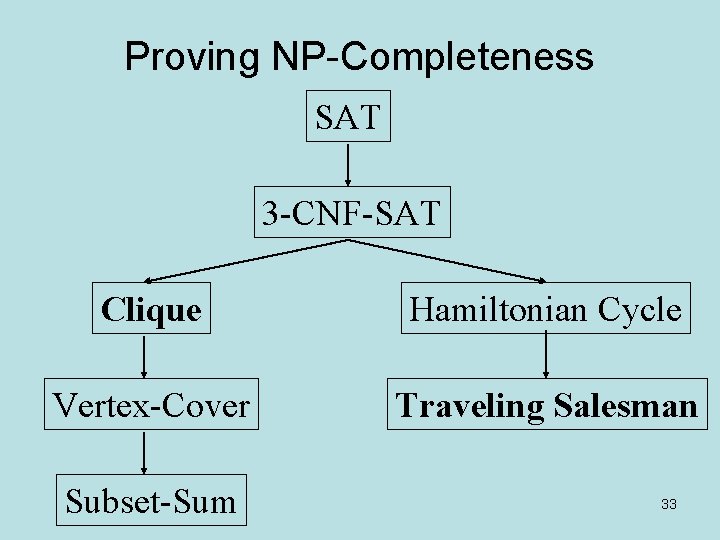
Proving NP-Completeness • What steps do we have to take to prove a problem A is NP-Complete? – Pick a known NP-Complete problem B – Reduce B to A • Describe a transformation that maps instances of B to instances of A, s. t. “yes” for A = “yes” for B • Prove the transformation works • Prove it runs in polynomial time – Oh yeah, prove A NP 27

Examples of NP-Complete problems • Cook’s theorem – Satisfiability is NP-complete • This was the first problem shown to be NPcomplete • Other problems – Graph coloring (= register allocation) – Hamiltonian path – Traveling salesman – Knapsack 28

Conjunctive Normal Form (CNF) • A logical (Boolean) variable is a variable that may be assigned the value true or false (p, q, r and s are Boolean variables) • A literal is a logical variable or the negation of a logical variable (p and Øq are literals) • A clause is a disjunction of literals ( (pÚqÚs) and (Øq Ú r) are clauses) 29

Conjunctive Normal Form (CNF) • A logical (Boolean) expression is in Conjunctive Normal Form if it is a conjunction of clauses. • The following expression is in conjunctive normal form: (pÚqÚs) Ù(Øq Ú r) Ù(Øp Ú r) Ù(Ør Ú s) Ù(ØpÚØsÚØq) 30

The Satisfiability problem • Is there a truth assignment to the n variables of a logical expression in Conjunctive Normal Form which makes the value of the expression true? – For the answer to be “yes”, all clauses must evaluate to true – Otherwise the answer is “no” • p=T, q=F, r=T and s=T is a truth assignment for: (pÚqÚs) Ù(Øq Ú r) Ù(Øp Ú r) Ù(Ør Ú s) Ù(ØpÚØsÚØq) 31

The Satisfiability problem • Theorem: Satisfiability is an NP-Complete problem. • Proof: – Satisfiability NP: Given a truth assignment of a Boolean formula consisting of n literals, it is clear that we can evaluate it in poly time. – Satisfiability NP-Hard: The proof involves reducing every problem in NP to Satisfiability in polynomial time. See Garey & Johnson. 32

Proving NP-Completeness SAT 3 -CNF-SAT Clique Hamiltonian Cycle Vertex-Cover Traveling Salesman Subset-Sum 33

NP completeness of CLIQUE • SAT reduces to CLIQUE – Given any input to SAT, we create a corresponding input to CLIQUE that will help us solve the original SAT problem – Specifically, for a SAT formula with K clauses, we construct a CLIQUE input that has a clique of size K if and only if the original Boolean formula is satisfiable 34

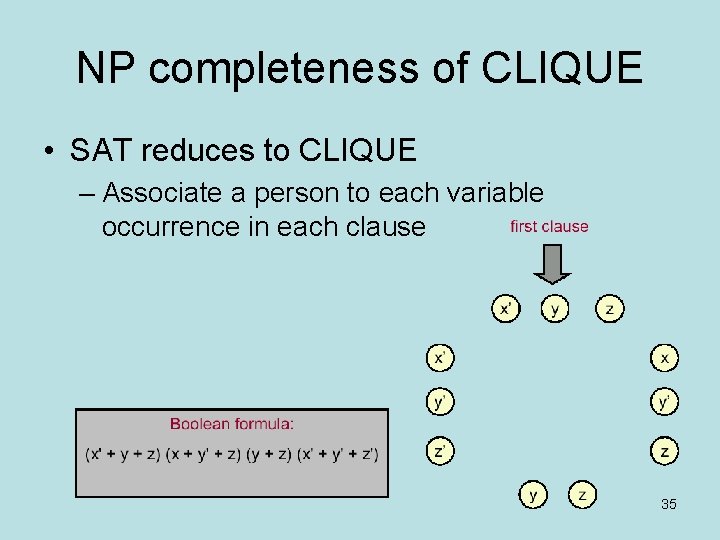
NP completeness of CLIQUE • SAT reduces to CLIQUE – Associate a person to each variable occurrence in each clause 35

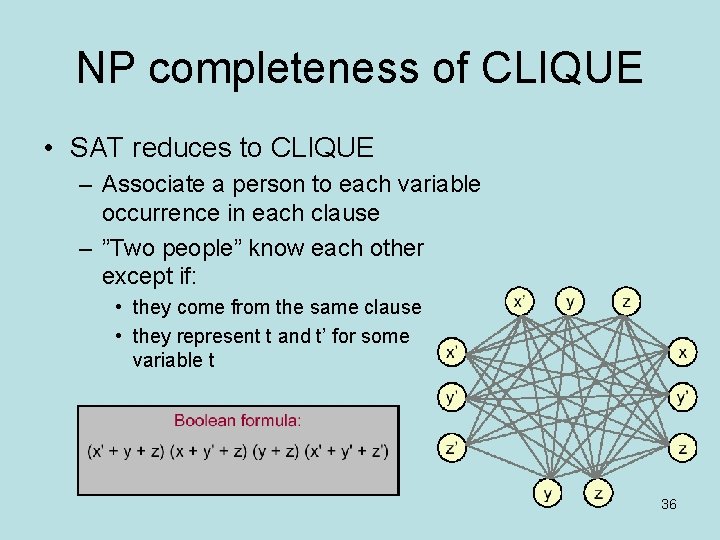
NP completeness of CLIQUE • SAT reduces to CLIQUE – Associate a person to each variable occurrence in each clause – ”Two people” know each other except if: • they come from the same clause • they represent t and t’ for some variable t 36

NP completeness of CLIQUE • SAT reduces to CLIQUE – Two people know each other except if: • they come from the same clause • they represent t and t’ for some variable t – Clique of size 4 Þ satisfiable assignment • set variable in clique to ”true” • (x, y, z) = (true, false) 37

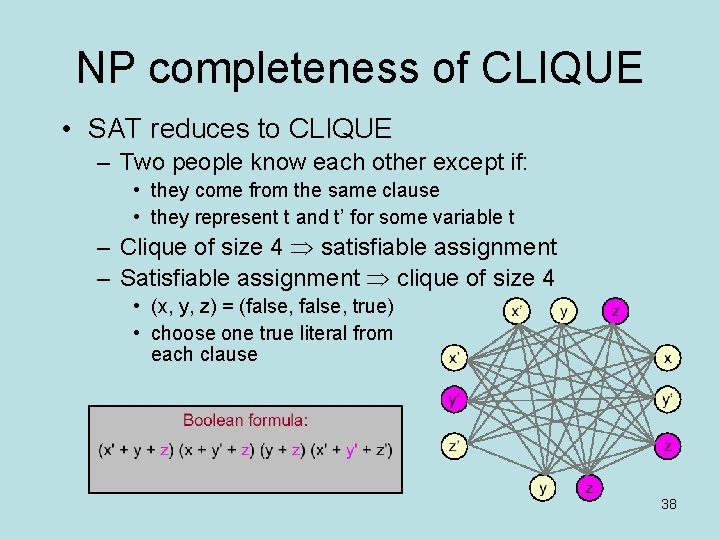
NP completeness of CLIQUE • SAT reduces to CLIQUE – Two people know each other except if: • they come from the same clause • they represent t and t’ for some variable t – Clique of size 4 Þ satisfiable assignment – Satisfiable assignment Þ clique of size 4 • (x, y, z) = (false, true) • choose one true literal from each clause 38

CLIQUE is NP-complete • CLIQUE is NP-complete – CLIQUE is in NP – SAT is in NP-complete – SAT reduces to CLIQUE • Hundreds of problems can be shown to be NP-complete that way… 39

NP completeness of CLIQUE • Show that the traveling salesman problem is NP -complete, assuming that the Hamiltonian cycle problem is NP-complete. – Prove that TSP NP (already done) • Guess: a sequence of cities • Verify: that it is a tour of cost less than B – Reduce the undirected Hamiltonian cycle problem to the TSP • So if we had a TSP-solver, we could use it to solve the Hamilitonian cycle problem in polynomial time 40

Ham. Cycle p TSP? • Transform input for Ham. Cycle into input for TSP – Ham. Cycle: Given unweighted graph G 1, does it have a Hamiltonian cycle? – TSP: Given weighted graph G 2 and B, is there a Hamiltonian cycle with total cost less than B? • Must convert unweighted graph to weighted 41

Ham. Cycle p TSP? • Convert unweighted graph to weighted – Add edges to G 1 to make a complete graph G 2 – Add weights as follows: • wt(i, j) is 0 if edge i, j is in G 1 (original graph for Ham. Cycle) • wt(i, j) is 1 if edge i, j is not in G 1 • G 1 has ham. cycle iff G 2 has TSP with B=0 – Can you see why? – Is this transformation polynomial? 42

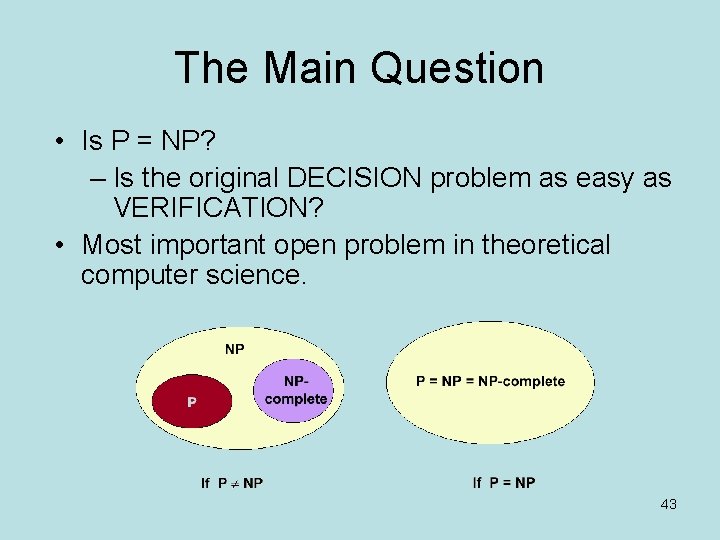
The Main Question • Is P = NP? – Is the original DECISION problem as easy as VERIFICATION? • Most important open problem in theoretical computer science. 43

The Big Picture • Summarizing: it is not known whether NP problems are tractable or intractable • But, there exist provably intractable problems – Even worse – there exist problems with running times unimaginably worse than exponential! • More bad news: there are provably noncomputable (undecidable) problems – There are no (and there will not ever be!) algorithms to solve these problems 44