Ch 1 Introduction Pattern Recognition and Machine Learning












- Slides: 23

Ch 1. Introduction Pattern Recognition and Machine Learning, C. M. Bishop, 2006. Summarized by K. I. Kim Biointelligence Laboratory, Seoul National University http: //bi. snu. ac. kr/ 1

Contents 1. 1 Example: Polynomial Curve Fitting l 1. 2 Probability Theory l ¨ 1. 2. 1 Probability densities ¨ 1. 2. 2 Expectations and covariance ¨ 1. 2. 3 Bayesian probabilities ¨ 1. 2. 4 The Gaussian distribution ¨ 1. 2. 5 Curve fitting re-visited ¨ 1. 2. 6 Bayesian curve fitting l 1. 3 Model Selection (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 2

Pattern Recognition Training set, l Target vector, l Training (learning) phase l ¨ Determine l Generalization ¨ Test set l Preprocessing ¨ Feature selection (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 3

Supervised, Unsupervised and Reinforcement Learning l Supervised Learning: with target vector ¨ Classification ¨ Regression l Unsupervised learning: w/o target vector ¨ Clustering ¨ Density estimation ¨ Visualization l Reinforcement learning: maximize a reward ¨ Trade-off between exploration & exploitation (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 4

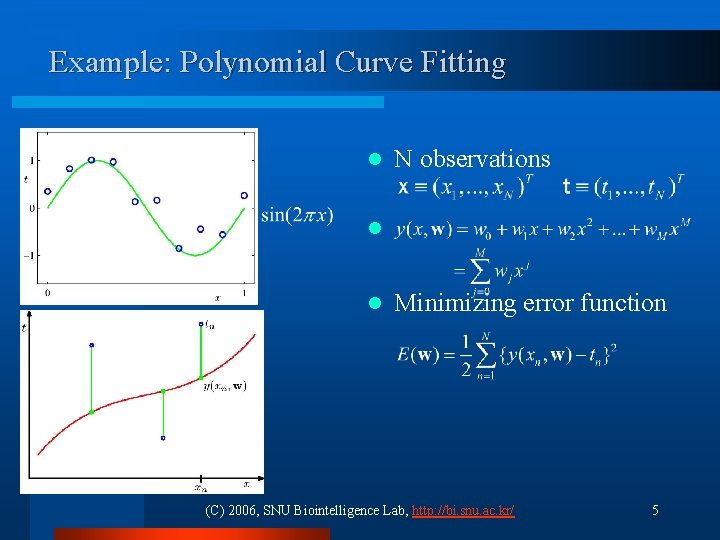
Example: Polynomial Curve Fitting l N observations l l Minimizing error function (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 5

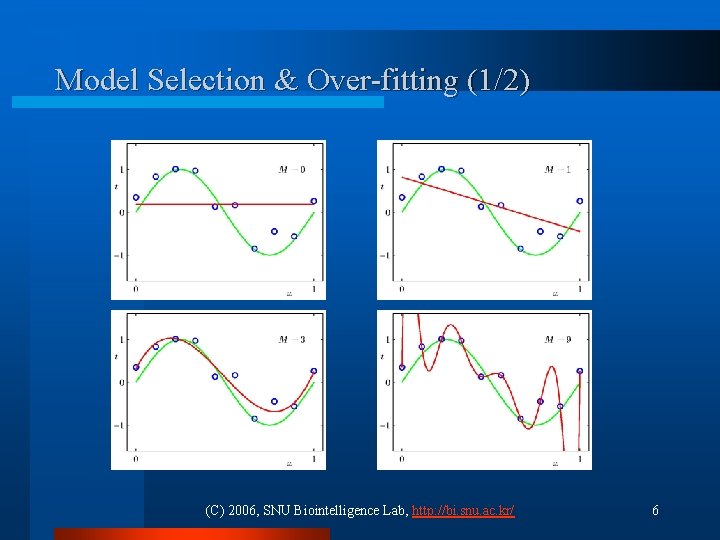
Model Selection & Over-fitting (1/2) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 6

Model Selection & Over-fitting (2/2) l RMS(Root-Mean-Square) Error Too large → Over-fitting l The more data, the better generalization l Over-fitting is a general property of maximum likelihood l (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 7

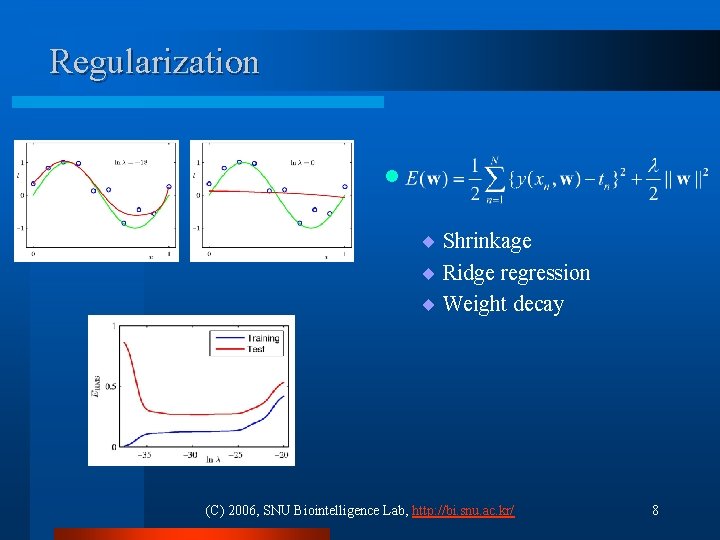
Regularization l ¨ Shrinkage ¨ Ridge regression ¨ Weight decay (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 8

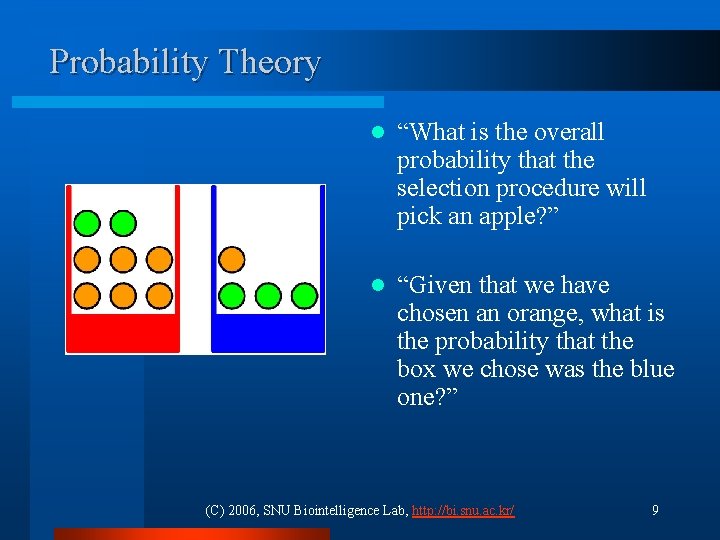
Probability Theory l “What is the overall probability that the selection procedure will pick an apple? ” l “Given that we have chosen an orange, what is the probability that the box we chose was the blue one? ” (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 9

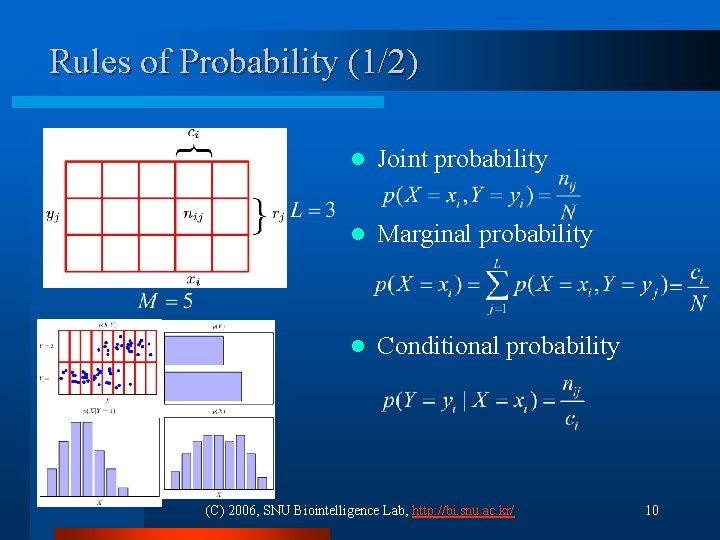
Rules of Probability (1/2) l Joint probability l Marginal probability l Conditional probability (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 10

Rules of Probability (2/2) l Sum rule l Production rule l Bayes’ theorem Likelihood Prior Posterior Normalizing constant (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 11

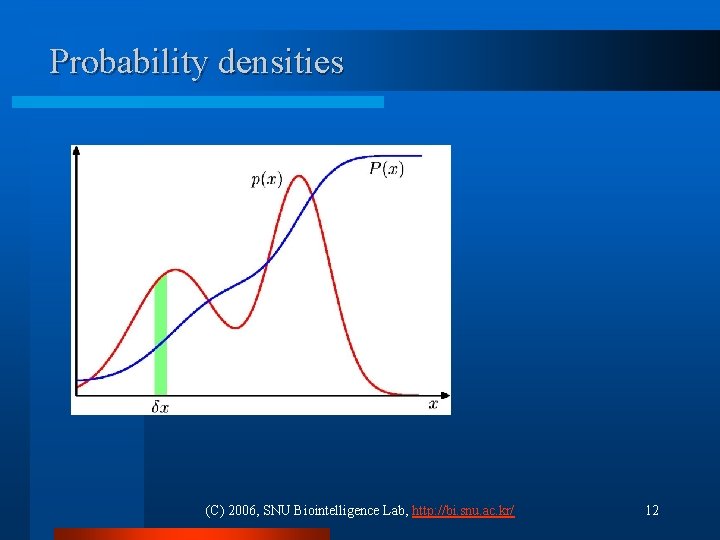
Probability densities (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 12

Expectations and Covariances l Expectation l Variance l Covariance (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 13

Bayesian Probabilities -Frequantist vs. Bayesian l l Likelihood: Frequantist ¨ w: a fixed parameter determined by 'estimator‘ < Maximum likelihood: Error function = < Error bars: Obtained by the distribution of possible data sets – Bootstrap l Bayesian ¨ a single data set ¨ a probability distribution w: the uncertainty in the parameters ¨ Prior knowledge < noninformative prior (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 14

Bayesian Probabilities -Expansion of Bayesian Application l Limited application of full Bayesian procedure ¨ from 18 th century ¨ Marginalize over the whole of parameter space l Markov chain Monte Carlo ¨ Small-scale problem l Highly efficient deterministic approximation schemes ¨ e. g. variational Bayes, expectation propagation ¨ Large-scale problem (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 15

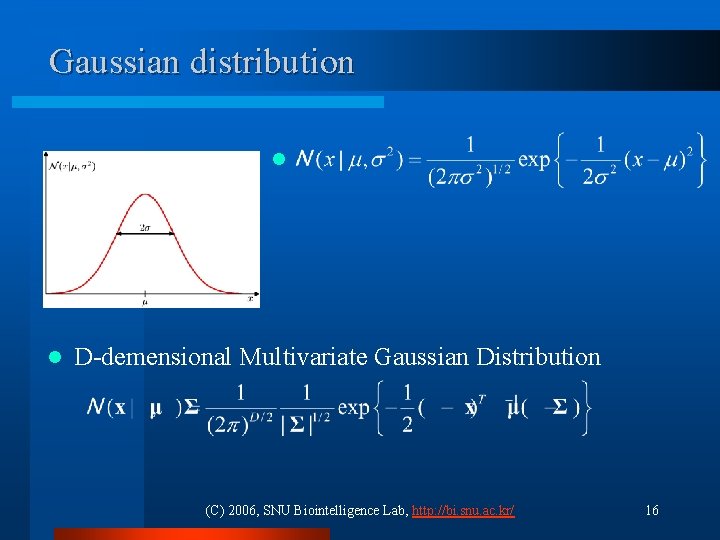
Gaussian distribution l l D-demensional Multivariate Gaussian Distribution (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 16

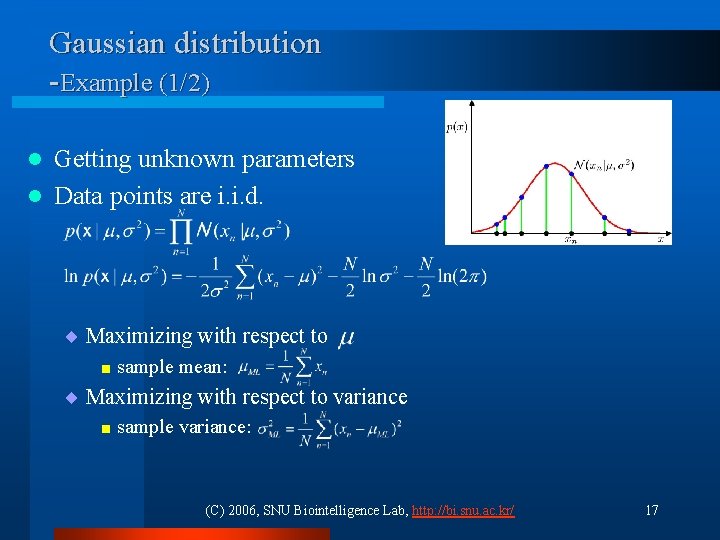
Gaussian distribution -Example (1/2) Getting unknown parameters l Data points are i. i. d. l ¨ Maximizing with respect to < sample mean: ¨ Maximizing with respect to variance < sample variance: (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 17

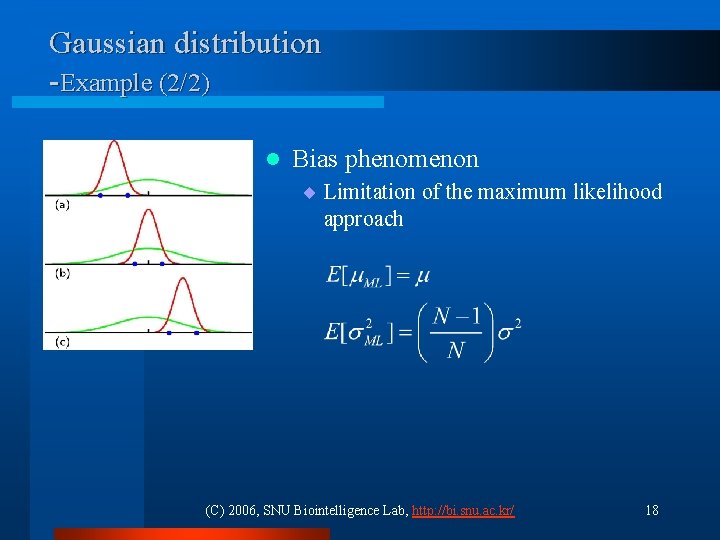
Gaussian distribution -Example (2/2) l Bias phenomenon ¨ Limitation of the maximum likelihood approach (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 18

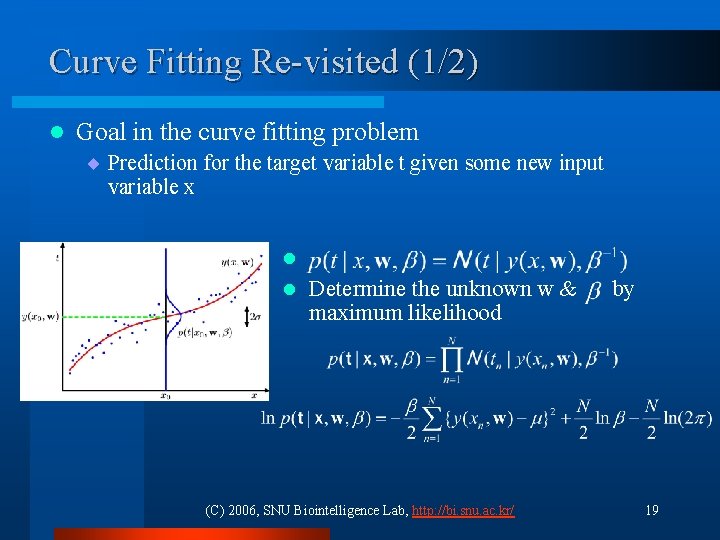
Curve Fitting Re-visited (1/2) l Goal in the curve fitting problem ¨ Prediction for the target variable t given some new input variable x l Determine the unknown w & by maximum likelihood l (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 19

Curve Fitting Re-visited (2/2) l ¨ maximizing likelihood = minimizing the sum-of-squares error function l l Predictive distribution (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 20

Maximum Posterior (MAP) l Add prior probability ¨ : hyperparameter ¨ Minimum of equals (1. 4) ¨ (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 21

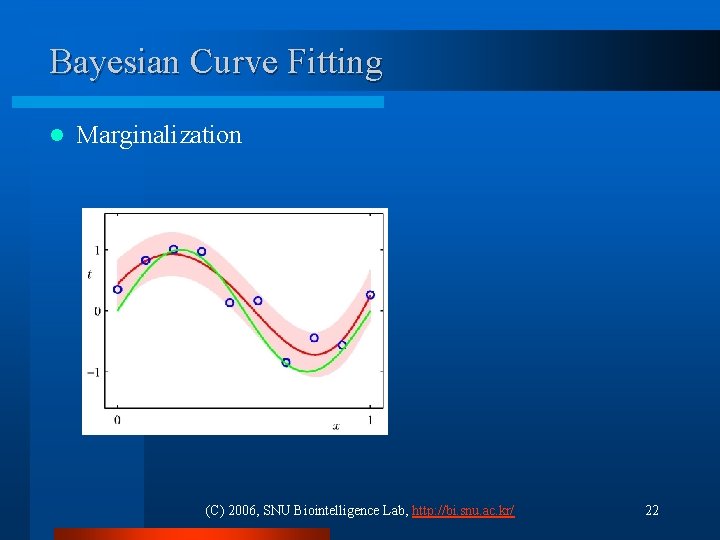
Bayesian Curve Fitting l Marginalization (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 22

Model Selection Proper model complexity → Good generalization & best model l Measuring the generalization performance l ¨ If data are plentiful, divide into training, validation & test set ¨ Otherwise, cross-validate < Leave-one-out technique < Drawbacks – Expensive computation – Using separate data → multiple complexity parameters ¨ New measures of performance < e. g. Akaike information criterion(AIC), Bayesian information criterion(BIC) (C) 2006, SNU Biointelligence Lab, http: //bi. snu. ac. kr/ 23