Ch 09 2 Approximation algorithm 2010617 1 NPComplete

Ch 09 _2 Approximation algorithm 2010/6/17 1

NP-Complete Problem � Enumeration � Branch an Bound � Greedy � Approximation ◦ PTAS ◦ K-Approximation ◦ No Approximation 2

Polynomial-Time Approximation Schemes �A problem L has a polynomial-time approximation scheme (PTAS) if it has a polynomial-time (1+ε)-approximation algorithm, for any fixed ε >0 (this value can appear in the running time). � For example, there is a PTAS for finding the maximum independent set problem on planar graphs. 3

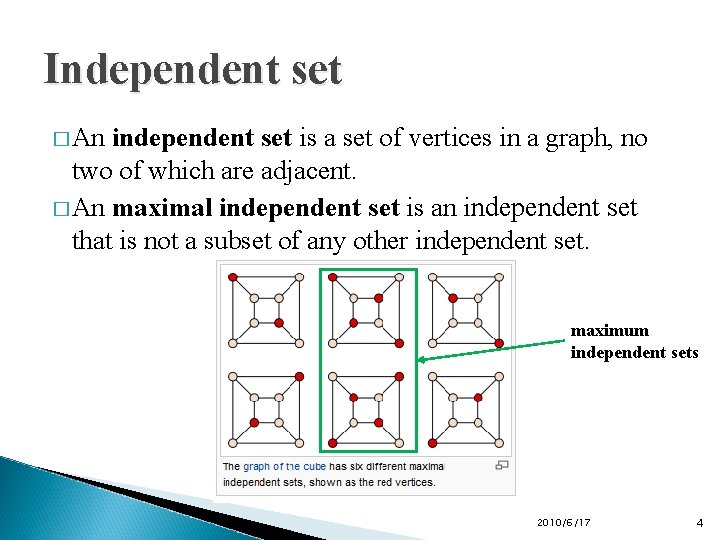
Independent set � An independent set is a set of vertices in a graph, no two of which are adjacent. � An maximal independent set is an independent set that is not a subset of any other independent set. maximum independent sets 2010/6/17 4

Finding the maximum independent set problem � The input is an undirected graph, and the output is a maximum independent set in the graph. � It is a NP-hard problem and it is also hard to approximate, and the decision problem is NP-Complete. there is a PTAS for finding the maximum independent set problem on planar graphs. � Fortunately, 2010/6/17 5

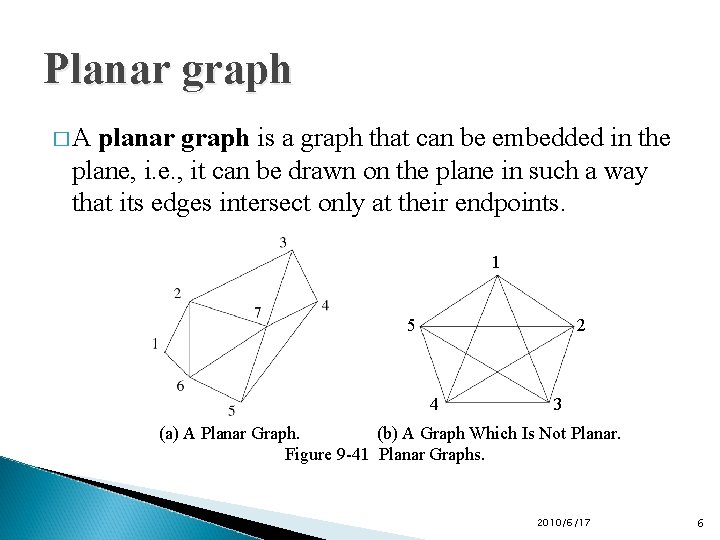
Planar graph �A planar graph is a graph that can be embedded in the plane, i. e. , it can be drawn on the plane in such a way that its edges intersect only at their endpoints. 1 5 2 4 3 (a) A Planar Graph. (b) A Graph Which Is Not Planar. Figure 9 -41 Planar Graphs. 2010/6/17 6

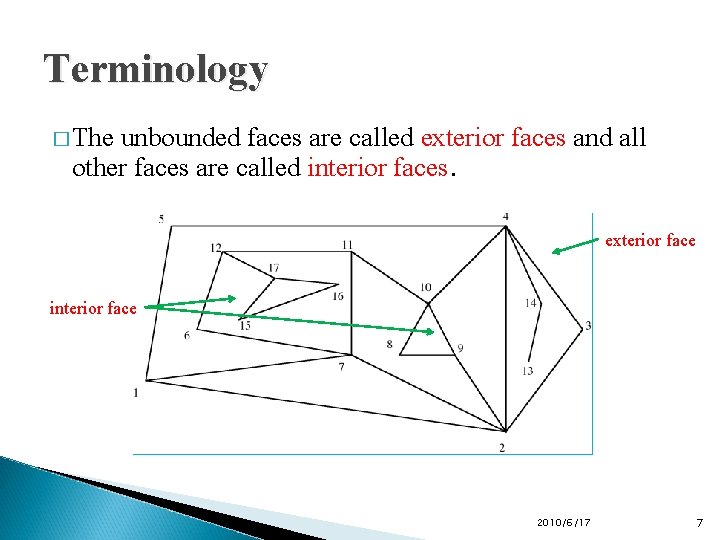
Terminology � The unbounded faces are called exterior faces and all other faces are called interior faces. exterior face interior face 2010/6/17 7

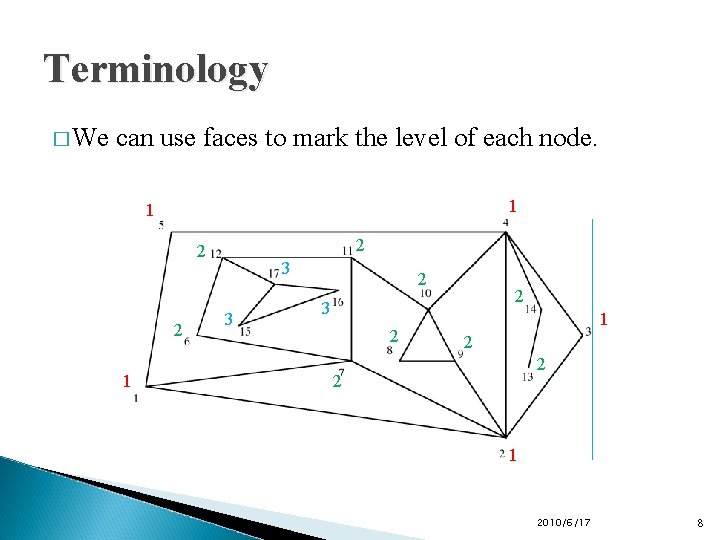
Terminology � We can use faces to mark the level of each node. 1 1 2 2 2 1 3 3 2 2 3 2 1 2 2 2 1 2010/6/17 8

Terminology �A graph is k-outerplanar if it has no nodes with level greater than k. Figure 9 -43 An Example of 2 -Outerplanar Graph. 2010/6/17 9

Property �Given an arbitrary planar graph G, we can decompose it into a set of k-outerplanar graphs. �For a k-outerplanar graph, an optimal solution for the maximum independent set problem can be found in O(8 kn) time through the dynamic programming approach where n is the number of vertices. 2010/6/17 10

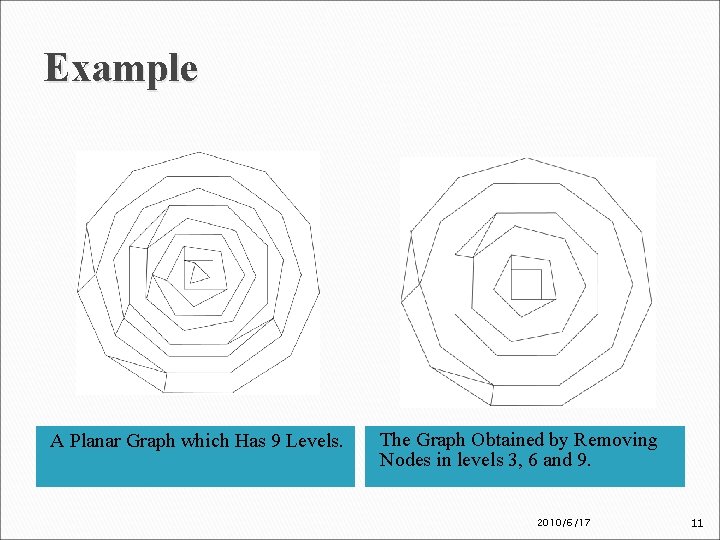
Example A Planar Graph which Has 9 Levels. The Graph Obtained by Removing Nodes in levels 3, 6 and 9. 2010/6/17 11

An Approximation Algorithm � Step 1. For all i = 0, 1, . . . , k, do ◦ (1. 1) Let Gi be the graph obtained by deleting all nodes with levels congruent to i (mod k + 1). The remaining subgraphs are all kouterplanar graphs. ◦ (1. 2) For each k-outerplanar graph, find its maximum independent set. Let Si denote the union of these solutions. � Step 2. Among S 0 , S 1 , . . . , Sk , choose the Sj with the maximum size and let it be our approximation solution SAPX. � The time-complexity of our approximation algorithm is obviously O(8 kkn). 2010/6/17 12

PTAS � Thus there is at least one r, such that at most of vertices in SOPT are at a level which is congruent to r (mod k + 1). � This means that the solution Sr obtained by deleting the nodes in class r from SOPT will have at least |SOPT| (1 )= |SOPT| nodes. 2010/6/17 13

PTAS � Therefore, |Sr| � According to our algorithm, ◦ |SAPX| |Sr| or �e = |SOPT| � Thus if we set k = -1, then the above formula becomes �e = E. 2010/6/17 14

Conclusion � This shows that for every given error bound E, we have a corresponding k to guarantee that the approximation solution differs from the optimum one within this error ratio. 2010/6/17 15