CFD 7 r Computer Fluid Dynamics 2181106 E

CFD 7 r Computer Fluid Dynamics 2181106 E 181107 Solvers, schemes SIMPLEx, upwind REDUCED lecture… Rudolf Žitný, Ústav procesní a zpracovatelské techniky ČVUT FS 2010

CFD 7 r FINITE VOLUME METHOD z y North y West Top E South x Bottom z x x FINITE CONTROL VOLUME x = Fluid element dx Finite size Infinitely small size

CFD 7 r A FVM diffusion problem 2 D W N P e E S Boundary conditions ØFirst kind (Dirichlet BC) ØSecond kind (Neumann BC) ØThird kind (Newton’s BC) Example: insulation q=0 Example: Finite thermal resistance (heat transfer coefficient )

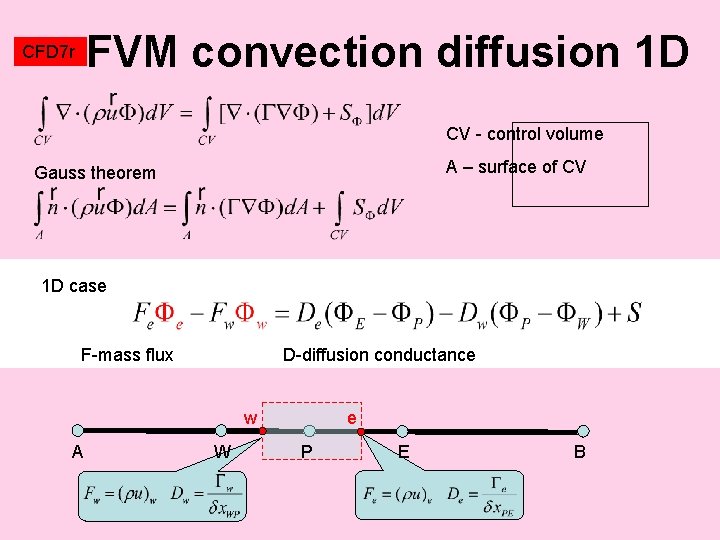
FVM convection diffusion 1 D CFD 7 r CV - control volume A – surface of CV Gauss theorem 1 D case F-mass flux D-diffusion conductance w A W e P E B

CFD 7 r FVM convection diffusion 1 D Relative importance of convective transport is characterised by Peclet number of cell (of control volume, because Pe depends upon size of cell) Prandt l Schmid t Thermal conductivity Binary diffusion coef

CFD 7 r FVM convection diffusion 1 D Methods differ in the way how the unknown transported values at the control volume faces ( w , e) are calculated (different interpolation techniques) Result can be always expressed in the form Properties of resulting schemes should be evaluated ØConservativeness ØBoundedness (positivity of coefficients anb) ØTransportivity (schemes should depend upon the Peclet number of cell)

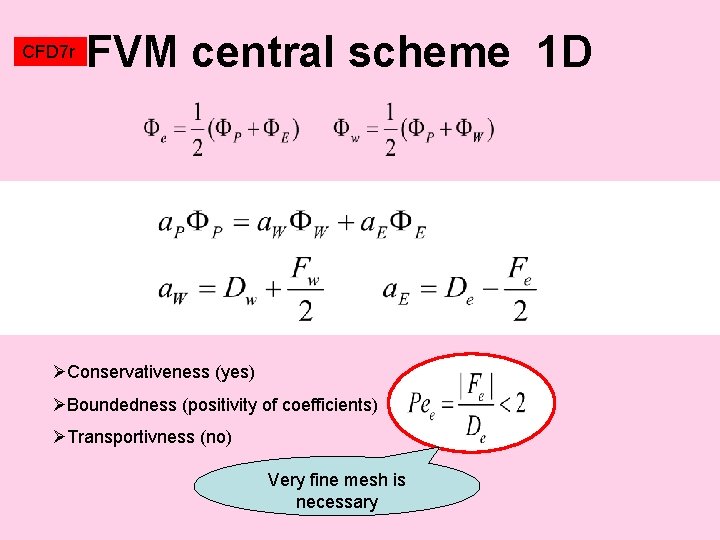
CFD 7 r FVM central scheme 1 D ØConservativeness (yes) ØBoundedness (positivity of coefficients) ØTransportivness (no) Very fine mesh is necessary

CFD 7 r FVM upwind 1 st order 1 D ØConservativeness (yes) ØBoundedness (positivity of coefficients) YES for any Pe ØTransportivness (YES) But at a prize of decreased order of accuracy (only 1 st order!!)

CFD 7 r FVM Upwind FLUENT Upwind of the first order Upwind of the second order f 0 1

CFD 7 r FVM exponential FLUENT Called power law model in Fluent ØExact solution of Projection of velocity to the direction r r 1 0 ØFor Pe<<1 the exponential profile is reduced to linear profile

CFD 7 r FVM dispersion / diffusion There are two basic errors caused by approximation of convective terms Numerical dispersion ØFalse diffusion (or numerical diffusion) – artificial smearing of jumps, discontinuities. Neglected terms in the Taylor series expansion of first derivatives (convective terms) represent in fact the terms with second derivatives (diffusion terms). So when using low order formula for convection terms (for example upwind of the first order), their inaccuracy is manifested by the artificial increase of diffusive terms (e. g. by increase of viscosity). The false diffusion effect is important first of all in the case when the flow direction is not aligned with mesh, see example ØDispersion (or aliasing) – causing overshoots, artificial oscillations. Dispersion means that different components of Fourier expansion (of numerical solution) move with different velocities, for example shorter wavelengths move slower than the velocity of flow. Numerical diffusion 1 u=v 0 - boundary condition, all values are zero in the right triangle (without diffusion)

CFD 7 r FVM Navier Stokes equations Different methods are used for numerical solution of Navier Stokes equations at Compressible flows (finite speed of sound, existence of velocity discontinuities at shocks) Explicit methods (e. g. Mac. Cormax) but also implicit methods (Beam-Warming scheme) are used. These methods will not be discussed here. Incompressible flows (infinite speed of sound) Vorticity and stream function methods (pressure is eliminated from NS equations). These methods are suitable especially for 2 D flows. Primitive variable approach (formulation in terms of velocities and pressure). Pressure represents a continuity equation constraint. Only these methods (pressure corrections methods SIMPLE, SIMPLER, SIMPLEC and PISO) using staggered and collocated grid will be discussed in this lecture. Beckman

CFD 7 r FVM Navier Stokes equations Example: Steady state and 2 D (velocities u, v and pressure p are unknown functions) This is equation for u This is equation for v This is equation for p? But pressure p is not in the continuity equation! Solution of this problem is in SIMPLE methods, described later

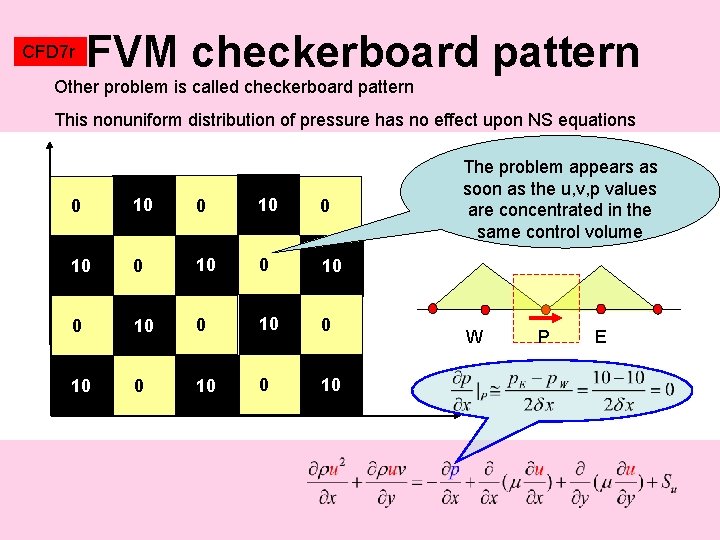
CFD 7 r FVM checkerboard pattern Other problem is called checkerboard pattern This nonuniform distribution of pressure has no effect upon NS equations 0 10 0 10 0 10 The problem appears as soon as the u, v, p values are concentrated in the same control volume W P E

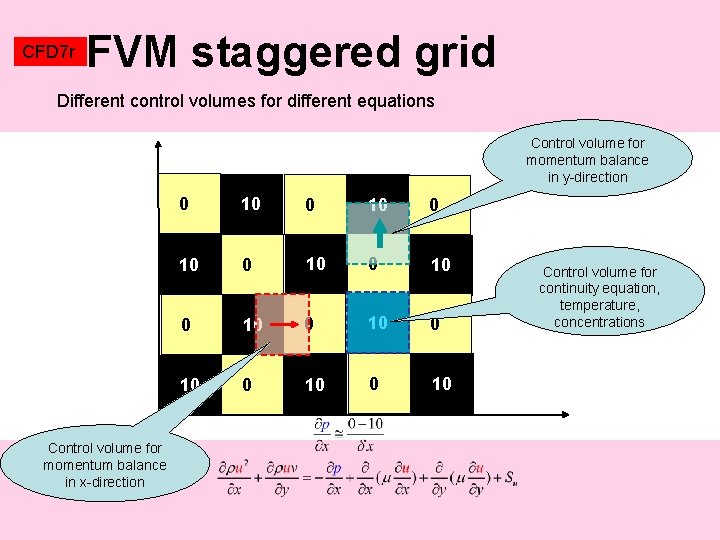
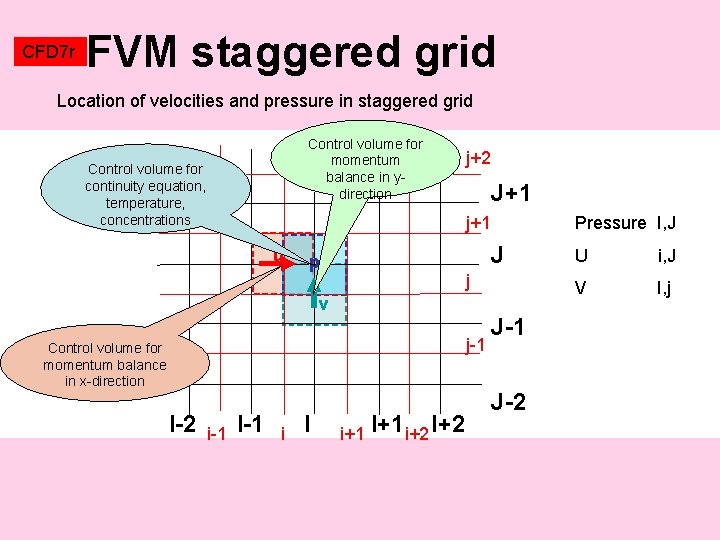
CFD 7 r FVM staggered grid Different control volumes for different equations Control volume for momentum balance in y-direction Control volume for momentum balance in x-direction 0 10 0 10 0 10 Control volume for continuity equation, temperature, concentrations

CFD 7 r FVM staggered grid Location of velocities and pressure in staggered grid Control volume for momentum balance in ydirection Control volume for continuity equation, temperature, concentrations j+2 J+1 j+1 u J p j v j-1 Control volume for momentum balance in x-direction I-2 i-1 I-1 i I Pressure I, J i+1 I+1 i+2 I+2 J-1 J-2 U i, J V I, j

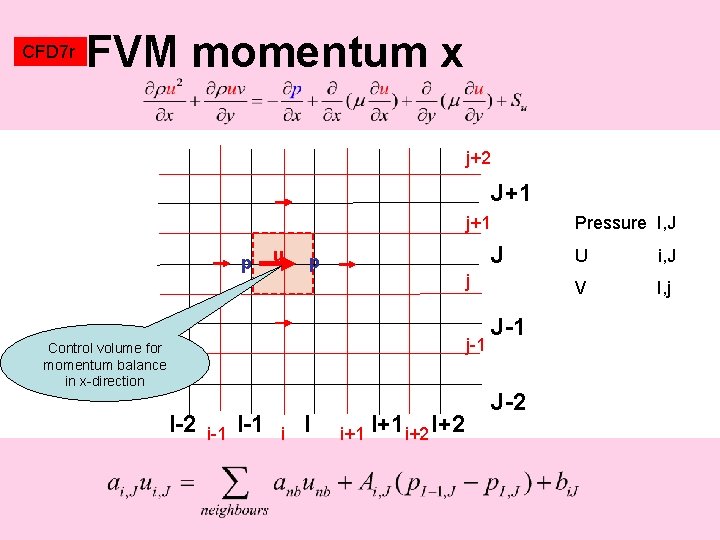
CFD 7 r FVM momentum x j+2 J+1 j+1 p u J p j j-1 Control volume for momentum balance in x-direction I-2 i-1 I-1 i I Pressure I, J i+1 I+1 i+2 I+2 J-1 J-2 U i, J V I, j

CFD 7 r FVM SIMPLE step 1 (velocities) Input: Approximation of pressure p*

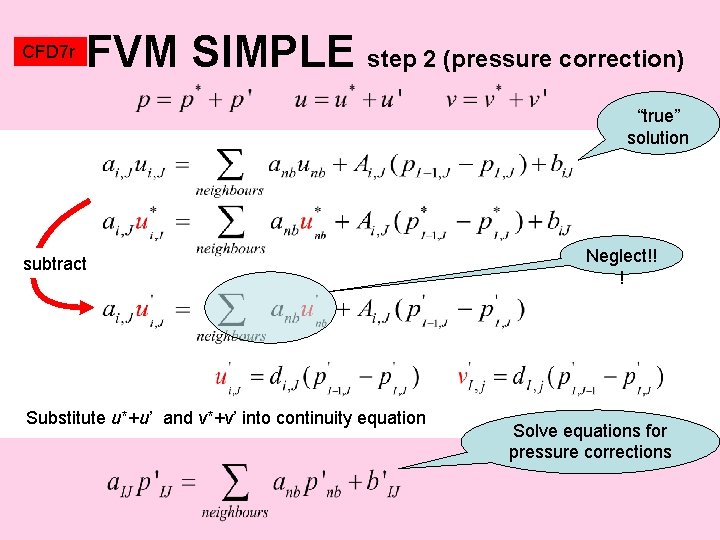
CFD 7 r FVM SIMPLE step 2 (pressure correction) “true” solution subtract Substitute u*+u’ and v*+v’ into continuity equation Neglect!! ! Solve equations for pressure corrections

CFD 7 r FVM SIMPLE step 3 (update p, u, v) Only these new pressures are necessary for next iteration Continue with the improved pressures to the step 1

CFD 7 r FVM SIMPLER (SIMPLE Revised) Idea: calculate pressure distribution directly from the Poisson’s equation

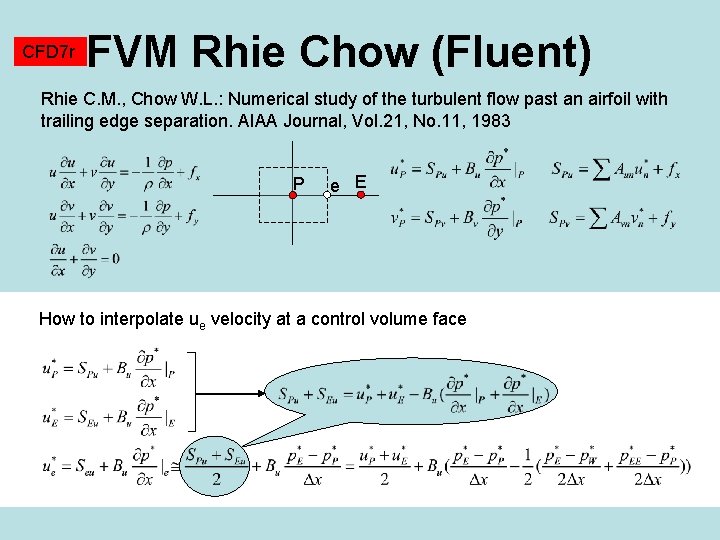
CFD 7 r FVM Rhie Chow (Fluent) The way how to avoid staggering (difficult implementation in unstructured meshes) was suggested in the paper Rhie C. M. , Chow W. L. : Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA Journal, Vol. 21, No. 11, 1983 This technique is called Rhie-Chow interpolation.

CFD 7 r FVM Rhie Chow (Fluent) Rhie C. M. , Chow W. L. : Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA Journal, Vol. 21, No. 11, 1983 P e E How to interpolate ue velocity at a control volume face

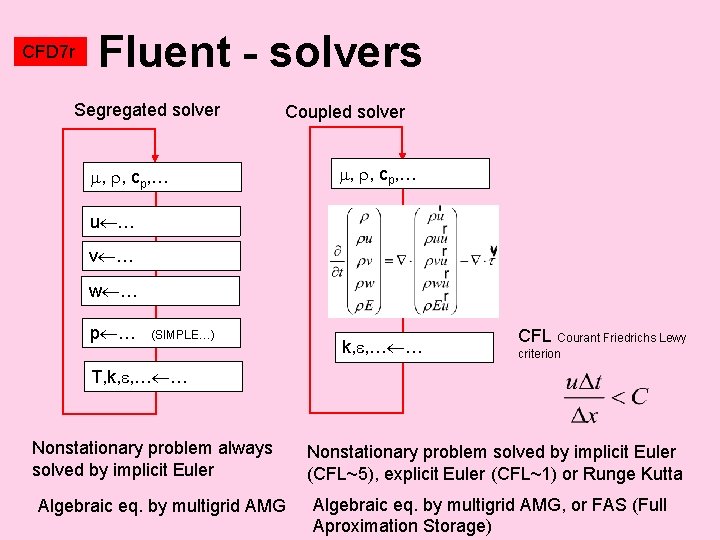
CFD 7 r Fluent - solvers Segregated solver Coupled solver , , cp, … u … v … w … p … (SIMPLE…) k, , … … CFL Courant Friedrichs Lewy criterion T, k, , … … Nonstationary problem always solved by implicit Euler Algebraic eq. by multigrid AMG Nonstationary problem solved by implicit Euler (CFL~5), explicit Euler (CFL~1) or Runge Kutta Algebraic eq. by multigrid AMG, or FAS (Full Aproximation Storage)

CFD 7 r FVM solvers Dalí

CFD 7 r FVM solvers Solution of linear algebraic equation system Ax=b ØTDMA – Gauss elimination tridiagonal matrix (obvious choice for 1 D problems, but suitable for 2 D and 3 D problems too, iteratively along the x, y, z grid lines – method of alternating directions ADI) ØPDMA – pentadiagonal matrix (suitable for QUICK), Fortran version ØCGM – Conjugated Gradient Method (iterative method: each iteration calculates increment of vector in the direction of gradient of minimised function – square of residual vector) ØMultigrid method (Fluent)

CFD 7 r Solver TDMA tridiagonal system MATLAB function x = TDMAsolver(a, b, c, d) %a, b, c, and d are the column vectors for the compressed tridiagonal matrix n = length(b); % n is the number of rows % Modify the first-row coefficients c(1) = c(1) / b(1); % Division by zero risk. d(1) = d(1) / b(1); % Division by zero would imply a singular matrix. for i = 2: n id = 1 / (b(i) - c(i-1) * a(i)); % Division by zero risk. c(i) = c(i)* id; % Last value calculated is redundant. d(i) = (d(i) - d(i-1) * a(i)) * id; end Forward step (elimination % Now back substitute. entries bellow diagonal) x(n) = d(n); for i = n-1: 1 x(i) = d(i) - c(i) * x(i + 1); end

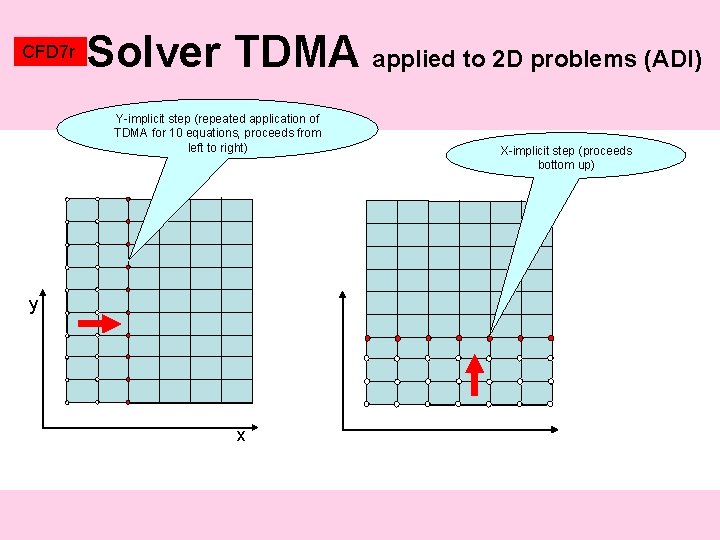
CFD 7 r Solver TDMA applied to 2 D problems (ADI) Y-implicit step (repeated application of TDMA for 10 equations, proceeds from left to right) y x X-implicit step (proceeds bottom up)

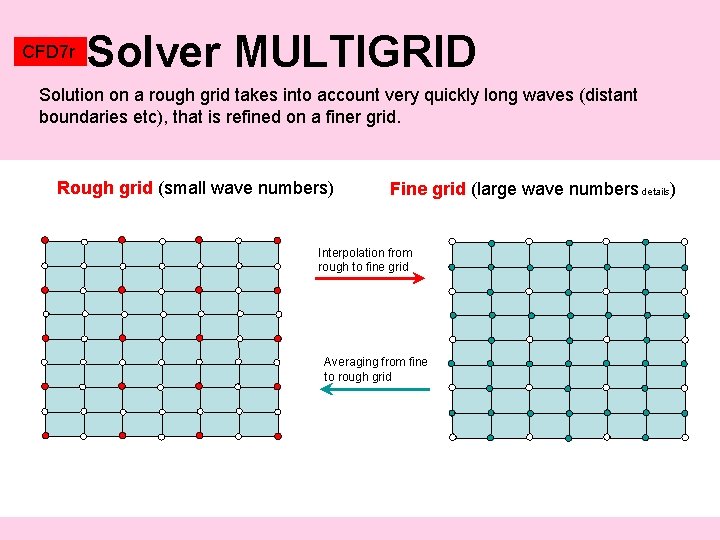
CFD 7 r Solver MULTIGRID Solution on a rough grid takes into account very quickly long waves (distant boundaries etc), that is refined on a finer grid. Rough grid (small wave numbers) Fine grid (large wave numbers details) Interpolation from rough to fine grid Averaging from fine to rough grid

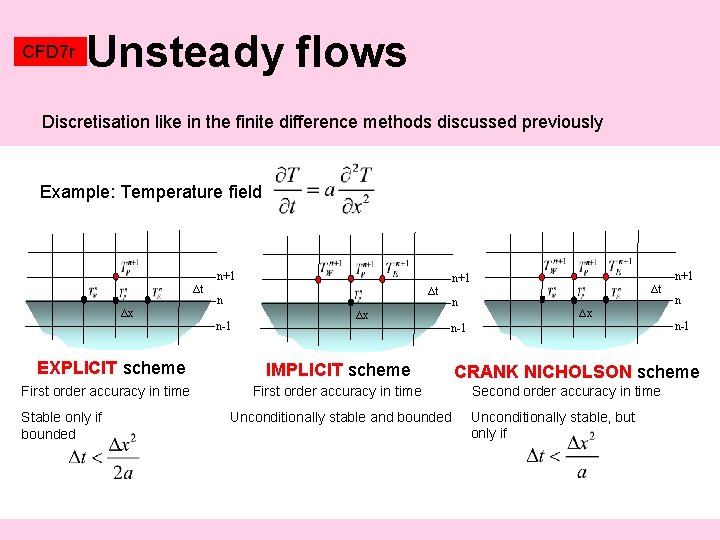
CFD 7 r Unsteady flows Discretisation like in the finite difference methods discussed previously Example: Temperature field ∆t ∆x n+1 ∆t n n-1 EXPLICIT scheme First order accuracy in time Stable only if bounded ∆x n+1 n ∆t ∆x First order accuracy in time Unconditionally stable and bounded n n-1 IMPLICIT scheme n+1 CRANK NICHOLSON scheme Second order accuracy in time Unconditionally stable, but only if

CFD 7 r FVM Boundary conditions are specified at faces of cells (not at grid points) ØINLET specified u, v, w, T, k, (but not pressure!) ØOUTLET nothing is specified (p is calculated from continuity eq. ) ØPRESSURE only pressure is specified (not velocities) ØWALL zero velocities, k. P, P calculated from the law of wall P y. P Recommended combinations for several outlets INLET OUTLET PRESSURE INLET PRESSURE OUTLET Forbidden combinations for several outlets PRESSURE OUTLET there is no unique solution because no flowrate is specified

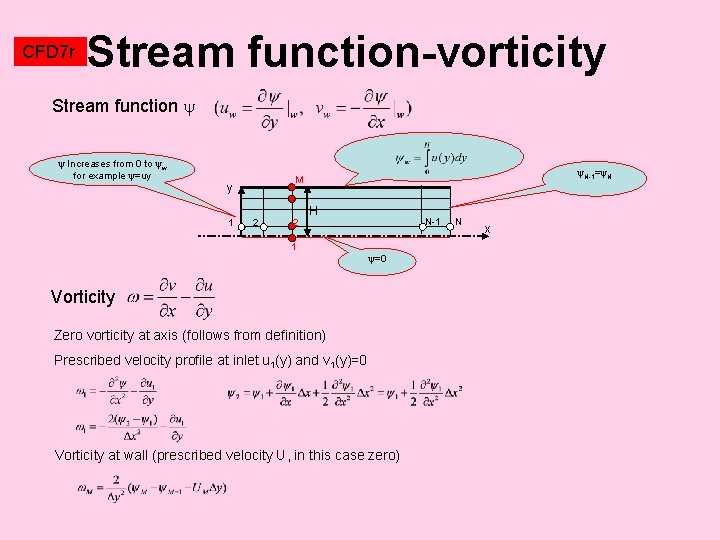
CFD 7 r Stream function-vorticity Introducing stream function and vorticity instead of primitive variables (velocities and pressure) eliminates the problem with the checkerboard pattern. Continuity equation is exactly satisfied. However the technique is used mostly for 2 D problems (it is sufficient to solve only 2 equations), because in 3 D problems 3 components of vorticity and 3 components of vector potential must be solved (comparing with only 4 equations when using primitive variable formulation of NS equations). Ghirlandaio

CFD 7 r Stream function-vorticity The best method for solution of 2 D problems of incompressible flows Pressure elimination Introduction vorticity (z-component of vorticity vector) Velocities expressed in terms of scalar stream function Vorticity expressed in terms of stream function

CFD 7 r Stream function-vorticity Three equations for u, v, p are replaced by two equations for , . Advantage: continuity equation is exactly satisfied. Vorticity transport is parabolic equation, Poisson equaion for stream function is eliptic. Lines of constant are streamlines (at wall =const). The no-slip condition at wall (prescribed velocities) must be reflected by boundary condition for vorticity How to do it, is shown in the next slide on example of flow in a channel

CFD 7 r Stream function-vorticity Stream function Increases from 0 to w for example =uy 1 N-1= N M y 2 2 H 1 N-1 =0 Vorticity Zero vorticity at axis (follows from definition) Prescribed velocity profile at inlet u 1(y) and v 1(y)=0 Vorticity at wall (prescribed velocity U, in this case zero) N x

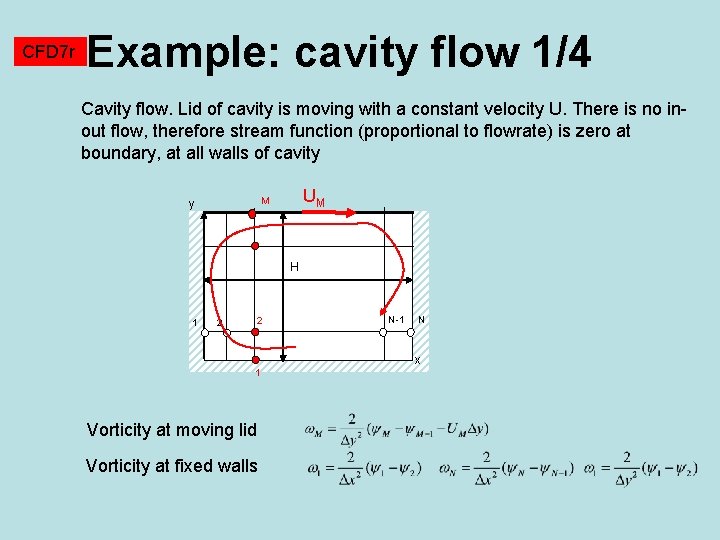
CFD 7 r Example: cavity flow 1/4 Cavity flow. Lid of cavity is moving with a constant velocity U. There is no inout flow, therefore stream function (proportional to flowrate) is zero at boundary, at all walls of cavity UM M y H 1 2 2 N-1 N x 1 Vorticity at moving lid Vorticity at fixed walls

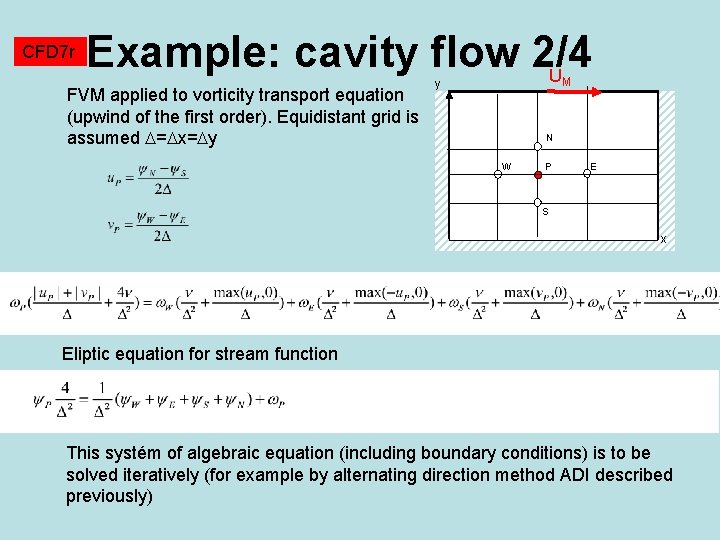
CFD 7 r Example: cavity flow 2/4 U FVM applied to vorticity transport equation (upwind of the first order). Equidistant grid is assumed = x= y M y N W P E S x Eliptic equation for stream function This systém of algebraic equation (including boundary conditions) is to be solved iteratively (for example by alternating direction method ADI described previously)

CFD 7 r Matlab Example: cavity flow 3/4 % tok v dutině. metoda vířivosti a pokutové funkice. Upwind. Metoda % střídavých směrů. h=0. 01; um=0. 0001; visc=1 e-6; % parametry site, a casovy krok relax=0. 5; n=21; d=h/(n-1); d 2=d^2; niter=50; psi=zeros(n, n); omega=zeros(n, n); u=zeros(n, n); v=zeros(n, n); a=zeros(n, 1); b=ones(n, 1); c=zeros(n, 1); r=zeros(n, 1); for iter=1: niter for i=1: n u(i, n)=um; end for i=2: n-1 for j=2: n-1 u(i, j)=(psi(i, j+1)-psi(i, j-1))/(2*d); v(i, j)=(psi(i-1, j)-psi(i+1, j))/(2*d); end %stream function x-implicit for j=2: n-1 for i=2: n-1 a(i)=-1/d 2; b(i)=4/d 2; c(i)=-1/d 2; r(i)=(psi(i, j-1)+psi(i, j+1))/d 2+ omega(i, j); end r(1)=0; r(n)=0; ps=tridag(a, b, c, r, n); for i=2: n-1 psi(i, j)=(1 -relax)*psi(i, j)+relax*ps(i); end %stream function y-implicit for i=2: n-1 for j=2: n-1 a(j)=-1/d 2; b(j)=4/d 2; c(j)=-1/d 2; r(j)=(psi(i-1, j)+psi(i+1, j))/d 2+ omega(i, j); end r(1)=0; r(n)=0; ps=tridag(a, b, c, r, n); for j=2: n-1 psi(i, j)=(1 -relax)*psi(i, j)+relax*ps(j); end % vorticity boundary conditions for i=1: n omega(i, n)=relax*omega(i, n)+(1 -relax)*2/d 2* (psi(i, n)-psi(i, n -1)-um*d); omega(i, 1)=relax*omega(i, 1)+(1 -relax)*2* (psi(i, 1)psi(i, 2))/d 2; omega(1, i)=relax*omega(1, i)+(1 -relax)*2*(psi(1, i)psi(2, i))/d 2; omega(n, i)=relax*omega(n, i)+(1 -relax)*2*(psi(n, i)-psi(n 1, i))/d 2; end %vorticity x-implicit for j=2: n-1 for i=2: n-1 up=u(i, j); vp=v(i, j); a(i)=-visc/d 2 -max(up, 0)/d; b(i)=4*visc/d 2+(abs(up)+abs(vp))/d; c(i)=-visc/d 2 -max(-up, 0)/d; r(i)=omega(i, j-1)*(visc/d 2+max(vp, 0)/d)+ omega(i, j+1)*(visc/d 2+max(-vp, 0)/d); end r(1)=omega(1, j); r(n)=omega(n, j); ps=tridag(a, b, c, r, n); for i=2: n-1 omega(i, j)=(1 -relax)*omega(i, j)+relax*ps(i); end %vorticity y-implicit for i=2: n-1 for j=2: n-1 up=u(i, j); vp=v(i, j); a(j)=-visc/d 2 -max(vp, 0)/d; b(i)=4*visc/d 2+(abs(up)+abs(vp))/d; c(j)=-visc/d 2 -max(-vp, 0)/d; r(j)=omega(i-, j)*(visc/d 2+max(up, 0)/d)+ omega(i+1, j)* (visc/d 2+max(-up, 0)/d); end r(1)=omega(i, 1); r(n)=omega(i, n); ps=tridag(a, b, c, r, n); for j=2: n-1 omega(i, j)=(1 -relax)*omega(i, j)+relax*ps(j); end end

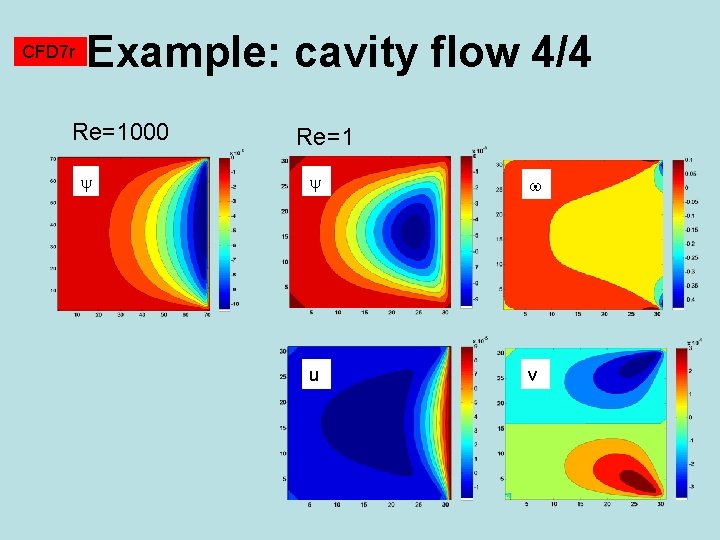
CFD 7 r Example: cavity flow 4/4 Re=1000 Re=1 u v

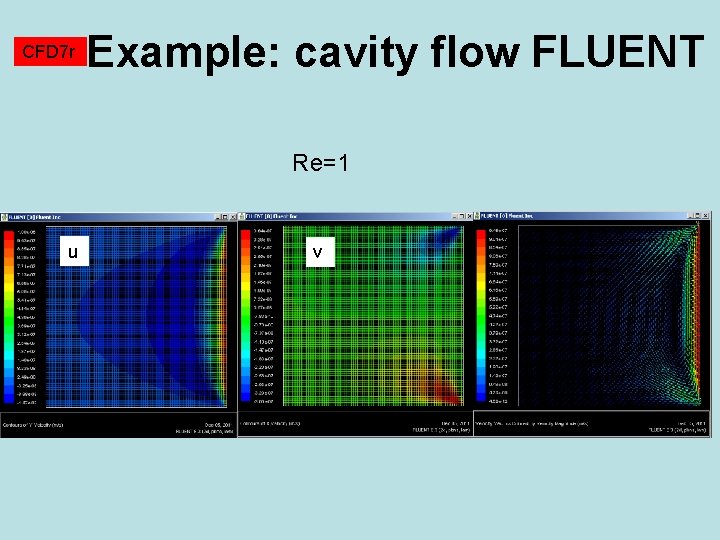
CFD 7 r Example: cavity flow FLUENT Re=1 u v