Certified Randomness from Quantum Supremacy 110100001101001 1110110110001010010011 010001111101111

Certified Randomness from Quantum Supremacy 110100001101001 1110110110001010010011 010001111101111 0100 Scott Aaronson (UT Austin) Beyond Crypto, Santa Barbara, CA, August 19, 2018 With a special bonus on: A connection between gentle measurement and differential privacy (joint work with Guy Rothblum)

Sampling-Based Quantum Supremacy Theoretical foundations: Terhal-Di. Vincenzo 2004, Bremner et al. 2011, A. -Arkhipov 2011, A. -Chen 2017. . . Showed that sampling the output distributions of various quantum systems is classically intractable under plausible assumptions… My previous line: Exciting because Google et al. might be able to do this in O(1) years, and because it will refute Oded Goldreich & Gil Kalai. Obviously, useless in itself… 110100001101001111011011001100010100100

Certified Random Bits: Who Needs ‘Em? For private use: Cryptographic keys (a big one!) For public use: Election auditing, lotteries, parameters for cryptosystems, zero-knowledge protocols, proofof-stake cryptocurrencies… Trivial Quantum Randomness Solution! |0 H Problem: What if your quantum hardware was backdoored by the NSA? (Like the DUAL_EC_DRBG pseudorandom generator was? ) Want to trust a deterministic classical computer only

Earlier Approach: Bell-Certified Randomness Generation Colbeck and Renner, Pironio et al. , Vazirani and Vidick, Coudron and Yuen, Miller and Shi… Upside: Doesn’t need a QC; uses only “current technology” (though loophole-free Bell violations are only ~2 years old) Downside: If you’re getting the random bits over the Internet, how do you know Alice and Bob were separated?

CHALLENGES New Approach: Randomness from SEED Quantum Supremacy Key Insight: A QC can solve certain sampling problems quickly —but under plausible hardness assumptions, it can only do so by sampling (and hence, generating real entropy) Upsides: Requires just a single device—perfect for remote use. Ideally suited to near-term QCs Caveats: Requires hardness assumptions and initial seed randomness. Verification (with my scheme) takes exp(n)

INHERENTLY REQUIRES QM Why? Because a classical server could always replace its randomness source by a pseudorandom one without the client being able to detect it Indeed, our protocol requires certain tasks (e. g. , finding heavy outputs of a quantum circuit) to be easy for QCs, and other tasks (e. g. , finding the same heavy outputs every time) to be hard for QCs!

The protocol does require pseudorandom challenges, but: Even if the pseudorandom generator is broken later, the truly random bits will remain safe (“forward secrecy”) Even if the seed was public, the random bits can be private The random bits demonstrably weren’t known to anyone, even the QC, before it received a challenge (freshness)

The Protocol 1. The classical client generates n-qubit quantum circuits C 1, …, CT pseudorandomly (mimicking a random ensemble) 2. For each t, the client sends Ct to the server, then demands a response St within a very short time In the “honest” case, the response is a list of k samples from the output distribution of Ct|0 n 3. The client picks O(1) random iterations t, and for each one, checks whether St solves “HOG” (Heavy Output Generation) 4. If these checks pass, then the client feeds S= S 1, …, ST into a classical randomness extractor, such as GUV (Guruswami. Umans-Vadhan), to get nearly pure random bits

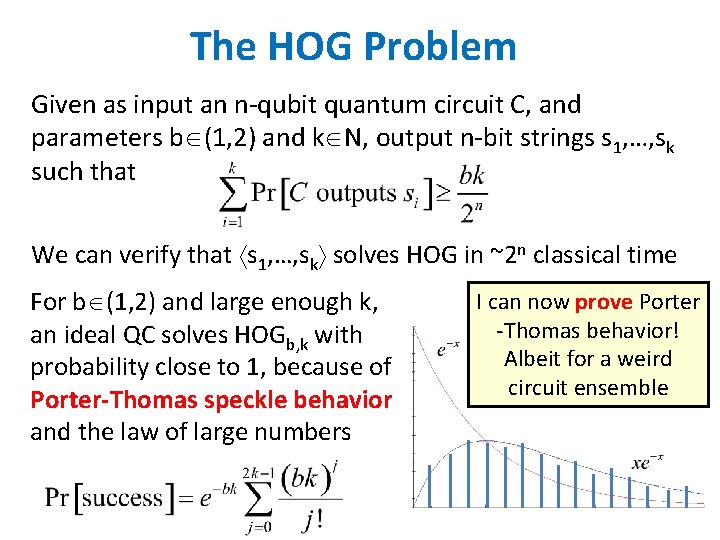
The HOG Problem Given as input an n-qubit quantum circuit C, and parameters b (1, 2) and k N, output n-bit strings s 1, …, sk such that We can verify that s 1, …, sk solves HOG in ~2 n classical time For b (1, 2) and large enough k, an ideal QC solves HOGb, k with probability close to 1, because of Porter-Thomas speckle behavior and the law of large numbers I can now prove Porter -Thomas behavior! Albeit for a weird circuit ensemble

Long List Hardness Assumption (LLHA) Arthur is given random access to a list of random n-qubit quantum circuits C 1, …, CM, as well as n-bit strings s 1, …, s. M, where (say) M=23 n. He’s promised that either (1) the si’s were drawn uniformly at random, or (2) each si was drawn from the output distribution of Ci. Then there’s no AM protocol wherein Arthur sends Merlin an n. O(1)-bit classical challenge, then Merlin sends back an n. O(1)-bit reply that convinces Arthur it’s case (2). Even if Arthur can do the verification using a 20. 49 n-time quantum computation, with 20. 49 n qubits of quantum advice.

Basic Theorem: Suppose LLHA holds. Let Q be a polynomial-time quantum algorithm that solves HOGb, k(C) with success probability at least q, averaged over all C. Then Q’s output distribution has at least of its mass (again, averaged over all circuits C) on outputs with probability at most 2 -0. 49 n Proof Idea: Using a “low-entropy” quantum algorithm Q to solve HOG, we design an AM protocol, based on Stockmeyer approximate counting, that violates LLHA— one where Merlin points Arthur to various highprobability outputs of Q to convince him he’s in case (2)

Pseudorandom Function Assumption (PRFA) There’s a family of efficiently-computable Boolean functions, gk: {0, 1}n {0, 1}, parameterized by an O(n)-bit seed k, such that for every 3 n-time quantum algorithm Q, Moreover, this is true even if Q is a PDQP algorithm (A. et al. 2014): a quantum algorithm that can contain both ordinary measurements and “non-collapsing” measurements LLHA and PRFA are strong assumptions, though both can be shown to hold in the random oracle model

Main Result Suppose LLHA and PRFA both hold, and that the server does at most n. O(1) quantum computation per iteration. Suppose also that we run the protocol, for T 2 n steps, and the client accepts with probability >½. Then conditioned on the client accepting, the output bits S are 1/exp(n (1))-close in variation distance to a distribution with min-entropy (Tn). Which means: the extractor will output (Tn) bits that are exponentially close to uniform Hard part: show accumulation of min-entropy across the T iterations. E. g. , rule out that the samples are correlated

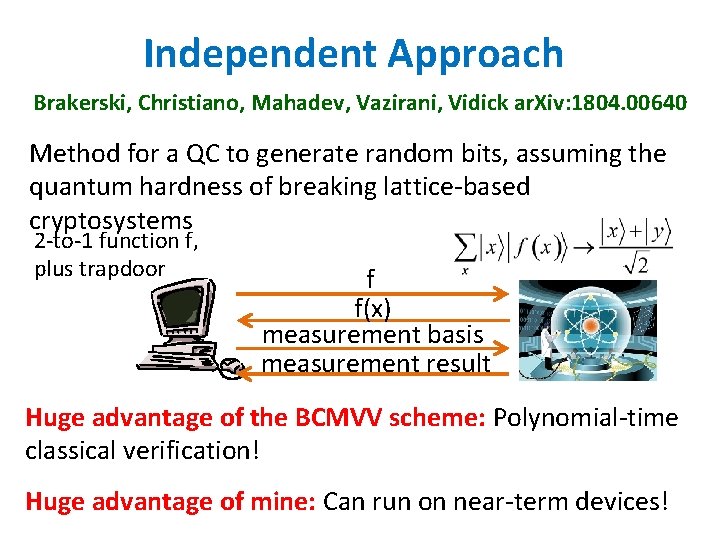
Independent Approach Brakerski, Christiano, Mahadev, Vazirani, Vidick ar. Xiv: 1804. 00640 Method for a QC to generate random bits, assuming the quantum hardness of breaking lattice-based cryptosystems 2 -to-1 function f, plus trapdoor f f(x) measurement basis measurement result Huge advantage of the BCMVV scheme: Polynomial-time classical verification! Huge advantage of mine: Can run on near-term devices!

Open Problems Can we get polynomial-time classical verification and near-term implementability at the same time? Can we get more and more certified randomness by sampling with the same circuit C over and over? Would Certifiedthe randomness generation: the for most greatly improve bit rate, remove the need a PRF plausible application for near-term QCs? Can we prove our scheme sound under less boutique All the weaknesses(without of sampling-based quantum complexity assumptions the quantum advice, supremacy experiments have strengths! non-collapsing measurements, long become list of circuits…)? What about soundness against adversaries that are entangled with the QC?

Gentle Measurement Bonus Measurements in QM are destructive … but not always! Given a quantum measurement M on n registers, we call M -gentle if for every product state = 1 n, and every possible outcome y of M, Example: Measuring the total Hamming weight of n unentangled qubits could be highly destructive But measuring the Hamming weight plus noise of order >> n is much safer!

Quantum Differential Privacy “Protecting the Privacy Rights of Quantum States” Given a quantum measurement M on n registers, we call M -DP if for every product state = 1 n, every ’ that differs from on only 1 register, and every possible outcome y of M, Example: Measuring the total Hamming weight of n unentangled qubits plus a noise term Hmmmm….

Our DP Gentleness Theorem (1) M is -gentle M is O( )-DP (2) M is -DP, and consists of a classical algorithm applied to the results of separate measurements on each register M can be implemented in a way that’s O( n)-gentle Could be seen as a quantum analogue of the known connection between DP and adaptive Notes: data analysis (Dwork et al. ) Both directions are asymptotically tight Restriction to product states is essential for part (2) (without it we only get O( n)-gentleness) Part (2) preserves efficiency, as long as the DP algorithm’s output distribution can be efficiently QSampled

Application: Shadow Tomography Theorem (A. , STOC’ 2018): Let be an unknown Ddimensional mixed state, and let E 1, …, EM be known 2 outcome measurements. Suppose we want to estimate Pr[Ei accepts ] to within for all i [M] w. h. p. We can do this given k where Using a quantum version of the Private Multiplicative Weights algorithm (Hardt-Rothblum 2010), together with our DP gentleness theorem, we can now get via a procedure that’s also online and gentle

Open Problems Prove a fully general DP gentleness theorem? In shadow tomography, does the number of copies of need to have any dependence on log D? Best lower bound we can show: k= ( -2 log M). But for gentle shadow tomography, can use known lower bounds from DP to show that k= ( (log D)) is needed Use quantum to say something new about classical DP?