Central Section or Projection Slice Theorem If Ffx

Central Section or Projection Slice Theorem If F{f(x, y)} = F(u, v) or F( , ) then F( , ) = F{ g (R) } The Fourier Transform of a projection at angle is a line in the Fourier transform of the image at the same angle. The Central Section Theorem is also referred to as the projectionslice theorem.

CT Reconstruction Methods - Filtered Back Projection π ∞ 0 -∞ ∫ d ∫ F-1{F{g (R) } • |p| } ( x cos + y sin - R) d. R Each projection is filtered to account for oversampling of lower spatial frequencies before back projection. Here filtering is done in the frequency domain

π ∞ 0 -∞ ∫ d ∫ [ g (R) * • c (R) ] ( x cos + y sin - R) d. R Same idea as filtered back projection, but filtering is done in projection domain. Here each projection is convolved with c (R) and then back projected. Describe c (R) C (p) = |p| c (R) = lim 2 ( 2 - 4π2 R 2) / ( 2 + 4π2 R 2)2 0

CT Artifacts: Beam Hardening I = I 0 e - ∫ dl I 0 (x, y) ln (I 0 / I) = ∫ dl Assumptions - zero width pencil beam - monoenergetic Bone • P Look at horizontal and vertical projection measure of attenuation at point P. How will bone affect the vertical projection?

Should get same answer for each projection. Normal emitted energy spectrum How does beam look after moving through bone tissue? Relative Intensity E Bone attenuates Cupping artifact Soft tissue cannot demonstrate its attenuation no photons to show it

First Generation CT Scanner From Webb, Physics of Medical Imaging

Physics of Medical Physics, Editor. Webb

Interpolation during Back Projection

Second Generation CT Scanner From Webb, Physics of Medical Imaging

rd 3 th 4 and Generation Scanners From Webb, Physics of Medical Imaging

Electron Beam CT

Krestel. Imaging Systems for Medical Diagnosis

Krestel. Imaging Systems for Medical Diagnosis

Sampling Requirements in CT • How many angles must we acquire? • Samples acquired by each projection are shown below as they fill the F(u, v) space. v u F(u, v)

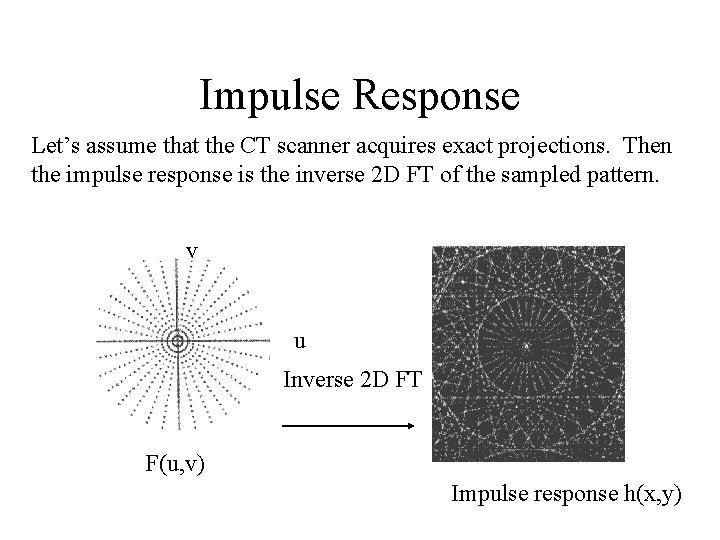
Impulse Response Let’s assume that the CT scanner acquires exact projections. Then the impulse response is the inverse 2 D FT of the sampled pattern. v u Inverse 2 D FT F(u, v) Impulse response h(x, y)

Impulse response • Bright white line points to correctly imaged impulse. • Inside of White circle shows region that is correctly imaged • Region outside of white circle suffers streak artifacts. • How big is the white circle? – How does it relate to the Impulse response h(x, y) number of angles? – Easier to think of in frequency domain

Recall: Band limiting and Aliasing F{g(x)} = G(u) is band limited to uc, (cutoff frequency) Thus G(u) = 0 for |u| > uc. uc To avoid overlap (aliasing) with a sampling interval X, uc Nyquist Condition: Sampling rate must be greater than twice the frequency component.

Apply to Imaging F{g(x, y)}= G(u, v) g(x, y) G(u, v) If we sample g(x, y) at intervals of X in x and y, then G(u, v) replicates v 1/X ^ G(u, v) u 1/X

Sampling in Frequency Domain If we sample in the frequency domain, then the image will replicate at 1/frequency sampling interval. DF G(u, v) Intersections depict sampling points. Let sampling interval in frequency domain be equal in each direction and be DF. Then we expect the images to replicate every 1/ DF

1/ DF = FOV

How many angles do we need? … D DF Three angles acquired from a CT exam are shown, each acquired D apart. Data acquisition is shown in the Fourier space using the Central Section Theorem. The radial spacing, DF , is the separation between the vertical hash marks on the horizontal projection. If we consider what the horizontal projection will look like as it is back projected, we can appreciate that 1/ DF = Field of View.

How many angles do we need? … D DF To avoid aliasing of any spatial frequencies, the spacing of the points in all directions must be no larger than DF . The largest spacing between points will come along the circumference. If we scale the radius of the circle so it has radius 1, the circumference will be 2 p. However, we only need projections to sample a distance of p since one projection will provide two points on the circle.

How many angles do we need? … D DF To avoid aliasing of any spatial frequencies, the spacing of the points in all directions must be no larger than DF . The largest spacing between points will come along the circumference. If we scale the radius of the circle so it has radius 1, the circumference will be 2 p. However, we only need projections to sample a distance of p since one projection will provide two points on the circle.

How many angles do we need? … D For a radius of 1 or diameter of 2, DF = 2/N where N is the number of detectors. That is, there are N hash marks ( samples) on the projection above. The spacing of points on the circumference will then be p/M where M is the number of projections. So the azimuthal spacing on the circumference, p/M, must be equal or smaller to the radial spacing 2/N. Solving for M gives M= p/2 * N

Azimuthal Sampling requires M angles = π/2 Ndetector elements Azimuthal Undersampling a) Sampling Pattern - frequency space or projections acquired b) Plot of one line of 2 D impulse response c) 2 D impulse response with undersampling d) Image of a Square e) What causes artifacts? Where do artifacts appear?