Central Force Motion Chapter 8 Introduction The 2

Central Force Motion Chapter 8 Introduction • The “ 2 body” Central Force problem! – We want to describe the motion of 2 bodies interacting through a central force. • Central Force A force between 2 bodies which is directed along the line between them. • A very important problem! Can it solve exactly! – Planetary motion & Kepler’s Laws. – Nuclear forces – Atomic physics (H atom), but we need the quantum mechanical version for this!

Center of Mass & Relative Coordinates, Reduced Mass Section 8. 2 & Outside Sources • Consider the general 3 dimensional, 2 body problem. 2 masses m 1 & m 2 Need 6 coordinates to describe the system. Use the components of the 2 position vectors r 1 & r 2 (with respect to an arbitrary origin, as in the figure).

• Now, specialize to the 2 body problem with conservative Central Forces only. The 2 bodies interact with a force F = F(r), which depends only on the distance r = |r 1 - r 2| between m 1 & m 2 (no angular dependences!). • F = F(r) is a conservative force A PE exists: U = U(r) F(r) = - U(r) r = -(d. U/dr) r The Lagrangian is: L = (½)[m 1|r 1|2 + m 2|r 2|2] - U(r)

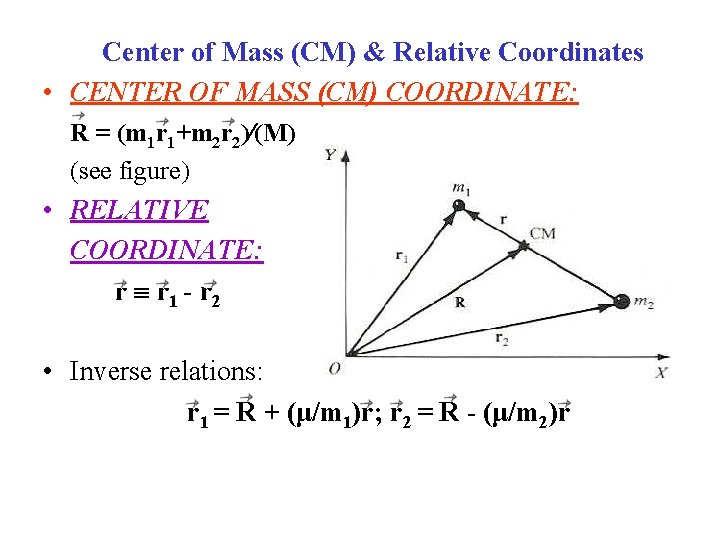
• Instead of the 6 components of the 2 vectors r 1 & r 2, Its usually much more convenient to transform to the (6 components of) the Center of Mass (CM) & Relative Coordinate systems. • CENTER OF MASS COORDINATE is defined as: R (m 1 r 1 +m 2 r 2) (m 1+m 2) Or: R = (m 1 r 1+m 2 r 2) (M) M (m 1+m 2) = total mass • RELATIVE COORDINATE is defined: r r 1 - r 2 • Its also convenient to define the Reduced Mass: μ (m 1 m 2) (m 1+m 2) A useful relation is: (1/μ) (1/m 1) +(1/m 2) • Algebra (student exercise!) gives inverse coordinate relations: r 1 = R + (μ/m 1)r; r 2 = R - (μ/m 2)r

Center of Mass (CM) & Relative Coordinates • CENTER OF MASS (CM) COORDINATE: R = (m 1 r 1+m 2 r 2) (M) (see figure) • RELATIVE COORDINATE: r r 1 - r 2 • Inverse relations: r 1 = R + (μ/m 1)r; r 2 = R - (μ/m 2)r

• The velocities [vi = ri, V = R, v = r] are related by v 1 = V + (μ/m 1)v; v 2 = V - (μ /m 2)v (1) • The Lagrangian is L = (½)[m 1|v 1|2 + m 2|v 2|2] - U(r) (2) • Combining (1) & (2) + algebra (student exercise!) gives the Lagrangian in terms of V, r, v: L = (½)M|V|2 + (½)μ|v|2 - U(r) Or: L = LCM + Lrel Where: LCM (½)M|V|2 & Lrel (½)μ|v|2 - U(r)

For the 2 body, Central Force Problem, the motion separates into 2 distinct parts! 1. The Center of Mass Motion, governed by: LCM (½)M|V|2 2. The Relative Motion, governed by Lrel (½)μ|v|2 - U(r)

For the 2 body, Central Force Problem, the motion separates into 2 distinct parts! 1. The center of mass motion: LCM (½)M|V|2 2. The relative motion: Lrel (½)μ|v|2 - U(r) Lagrange’s Equations for the 3 components of the CM coordinate vector R clearly gives equations of motion independent of r. Lagrange’s Equations for the 3 components of the relative coordinate vector r clearly gives equations of motion independent of R. • By transforming coordinates from (r 1, r 2) to (R, r): The 2 body problem has been separated into 2 INDEPENDENT one body problems!

Center of Mass (CM) Motion • The motion of the CM is governed by LCM (½)M|V|2 (assuming no external forces). • Let R = (X, Y, Z) 3 Lagrange Equations. Each looks like: ( [LCM]/ X) - (d/dt)( [LCM]/ X) = 0 [LCM]/ X = 0 (d/dt)( [LCM]/ X) = 0 X = 0, The CM acts like a free particle! • Solution: X = Vx 0 = constant. Determined by initial conditions! X(t) = X 0 + Vx 0 t , exactly like a free particle! • Similar eqtns for Y, Z: R(t) = R 0 + V 0 t , like a free particle! • The motion of the CM is identical to the trivial motion of a free particle. It corresponds to a uniform translation of the CM through space. Trivial & uninteresting!

We’ve transformed the 2 body, Central Force Problem, motion separates into 2 one body problems, ONE OF WHICH IS TRIVIAL! 1. The center of mass motion is governed by: LCM (½)M|V|2 As we’ve just seen, this motion is trivial! 2. The relative motion is governed by Lrel (½)μ|v|2 - U(r) • Clearly, all of the interesting physics is in the relative motion part! We now focus on it exclusively!

Relative Motion • The Relative Motion is governed by Lrel (½)μ|v|2 - U(r) – Assuming no external forces. – Henceforth Lrel L (drop the subscript) – For convenience, take the origin of coordinates at the CM: R = 0. See figure. r 1 = (μ/m 1)r & r 2 = - (μ/m 2)r μ (m 1 m 2) (m 1+m 2) (1/μ) (1/m 1) +(1/m 2)

• The 2 body, central force problem has been formally reduced to an EQUIVALENT ONE BODY PROBLEM in which the motion of a “particle” of mass μ in a potential U(r) is what is to be determined! – The full solution superimposes the uniform, free particlelike translation of the CM onto the relative motion solution! – If desired, if we get r(t), we can get r 1(t) & r 2(t) from the relations on the previous page. Usually, the relative motion (or orbit) only is wanted & we stop at r(t).

Conservation Theorems “First Integrals of the Motion” Section 8. 3 • Our System is effectively a “particle” of mass μ moving in a central force field described by a potential U(r). – Note: U(r) depends only on r = |r 1 - r 2| = distance of the “particle” from the force center. There is no orientation dependence! The system has spherical symmetry Rotation about any fixed axis cannot affect the equations of motion.

Angular Momentum • In Section 7. 9, it was shown: Spherical Symmetry Total Angular Momentum is conserved. That is: L = r p = const (magnitude & direction!) Angular Momentum Conservation! r & p always lie in a plane L, which is fixed in space (figure). The problem has now effectively been reduced from a 3 d to a 2 d problem (motion in a plane)!

• Remarkable enough to emphasize again! We started with a 6 d, 2 body problem. We reduced it to 2, 3 d 1 body problems, one (the CM motion) of which is trivial. Angular momentum conservation effectively reduces second 3 d problem (relative motion) from 3 d to 2 d (motion in a plane)! • The Lagrangian is: L = (½)μ|v|2 - U(r) • Motion in a plane Use plane polar coordinates to do the problem: L = (½)μ (r 2 + r 2θ 2) - U(r)

L = (½)μ (r 2 + r 2θ 2) - U(r) • The Lagrangian is cyclic in θ The corresponding generalized momentum pθ is conserved: pθ ( L/ θ) = μr 2θ; ( L/ θ) - (d/dt)[( L/ θ)]= 0 pθ = 0, pθ = constant = μr 2θ • PHYSICS: pθ = μr 2θ = The (magnitude of the) angular momentum about an axis to the plane of the motion. Conservation of angular momentum! • The problem symmetry has allowed us to integrate one equation of motion (the θ equation). pθ A “First Integral” of the motion. It is convenient to define: pθ = μr 2θ = constant.

L = (½)μ (r 2 + r 2θ 2) - U(r) • Using the angular momentum = μr 2θ = const, the Lagrangian is: L = (½)μr 2 + [( 2)/(2μr 2)] - U(r) • 2 nd Term: The KE due to the θ degree of freedom! • Symmetry & the resulting conservation of angular momentum has reduced the effective 2 d problem (2 degrees of freedom) to an effective (almost) 1 d problem! The only non-trivial equation of motion is for the single generalized coordinate r! • Could set up & solve the problem using the above Lagrangian. Instead, follow the authors & do it with energy.

Kepler’s 2 nd Law • First, more discussion of the consequences of the constant angular momentum = μr 2θ • Note that could be < 0 or > 0. • Geometric interpretation: = constant. See figure: • In describing the “particle” path r(t), in time dt, the radius vector sweeps out an area d. A = (½)r 2 dθ

• In dt, the radius vector sweeps out an area d. A = (½)r 2 dθ – Define AREAL VELOCITY (d. A/dt) = (½)r 2(dθ/dt) = (½)r 2θ (1) But = μr 2θ = constant θ = ( /μr 2) (2) • Combine (1) & (2): (d. A/dt) = (½)( /μ) = constant! The areal velocity is constant in time! The radius vector from the origin sweeps out equal areas in equal times Kepler’s 2 nd Law • Derived empirically by Kepler for planetary motion. A general result for central forces! Not limited to gravitational forces (r-2)

Momentum & Energy • The linear momentum of the system is conserved: – Linear momentum of the CM. Uninteresting free particle motion! • The total mechanical energy is E also conserved since we assumed that the central force is conservative: E = T + U = const = (½)μ(r 2 + r 2θ 2) + U(r) • Recall that the angular momentum is: μr 2θ= const θ = [ /(μr 2)] E = (½)μr 2 + [ 2 (2μr 2)] + U(r) = const A “second integral” of the motion