Centered Discrete Fractional Fourier Transform Linear Chirp Signals

Centered Discrete Fractional Fourier Transform & Linear Chirp Signals Balu Santhanam & Juan G. Vargas- Rubio SPCOM Laboratory, Department of E. C. E. University of New Mexico, Albuquerque Email: bsanthan, jvargas@ece. unm. edu 11 th DSP Workshop Taos Ski Valley, NM 2004 1

ABSTRACT n Centered discrete fractional Fourier transform (CDFRFT), based on the Grünbaum commutor produces a impulse-like transform for discrete linear chirp signals. n Relationship between chirp rate & angle of the transform approximated by a simple tangent function. n Multi-angle CDFRFT computed using the FFT & used to estimate the chirp rate of monocomponent & twocomponent chirps. 11 th DSP Workshop Taos Ski Valley, NM 2004 2

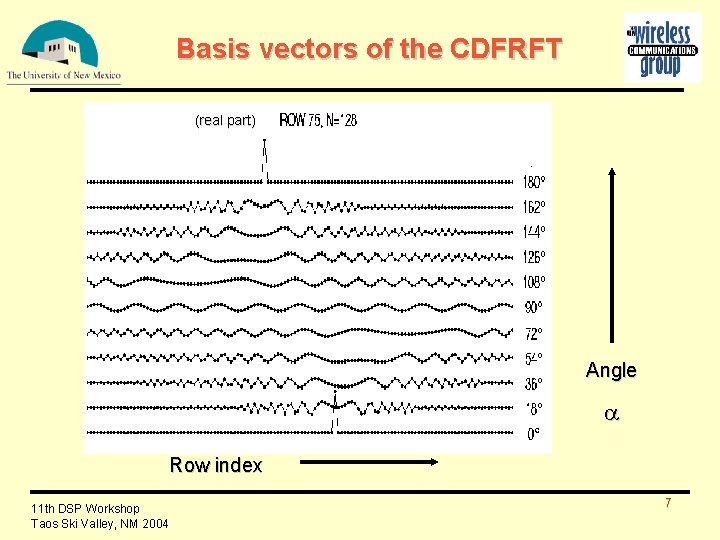
Why Grunbaum eigenvectors? n Grünbaum tridiagonal commutor converges to Hermite--Gauss differential operator as N ! 1 n Grünbaum commutor furnishes a full orthogonal basis of eigenvectors independent of N. n Grünbaum eigenvectors are better approximations to Hermite-Gauss functions. n Corresponding CDFRFT is efficient in concentrating a discrete linear chirp signal. 11 th DSP Workshop Taos Ski Valley, NM 2004 3

The Centered DFRFT n Define CDFRFT for parameter as: § VT matrix of Grünbaum eigenvectors. § L 2 / diagonal matrix with elements lk=e-jk. n CDFRFT in terms of the individual eigenvectors vk via single expression for N even or odd: 11 th DSP Workshop Taos Ski Valley, NM 2004 4

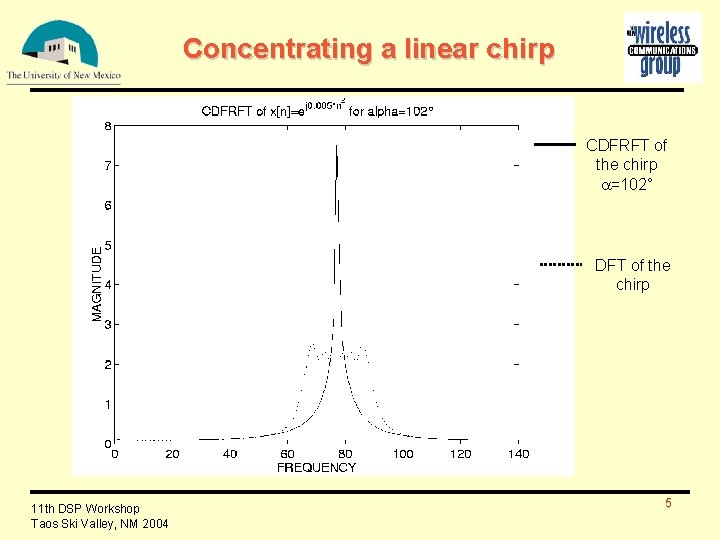
Concentrating a linear chirp CDFRFT of the chirp =102° DFT of the chirp 11 th DSP Workshop Taos Ski Valley, NM 2004 5

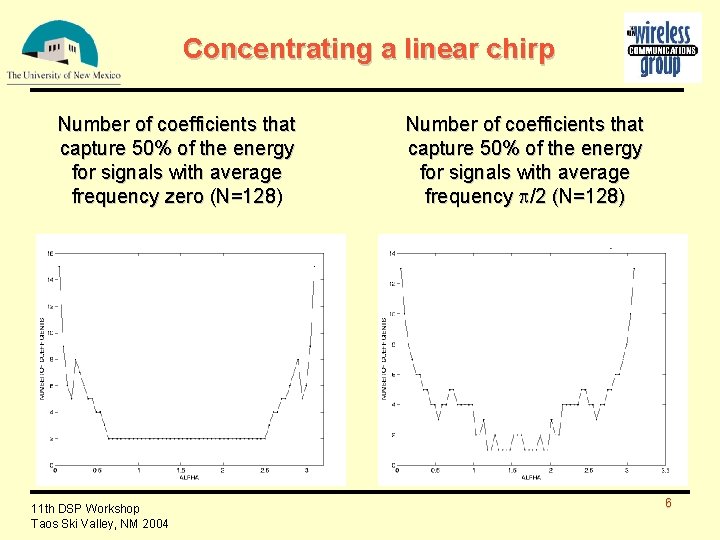
Concentrating a linear chirp Number of coefficients that capture 50% of the energy for signals with average frequency zero (N=128) 11 th DSP Workshop Taos Ski Valley, NM 2004 Number of coefficients that capture 50% of the energy for signals with average frequency /2 (N=128) 6

Basis vectors of the CDFRFT (real part) Angle Row index 11 th DSP Workshop Taos Ski Valley, NM 2004 7

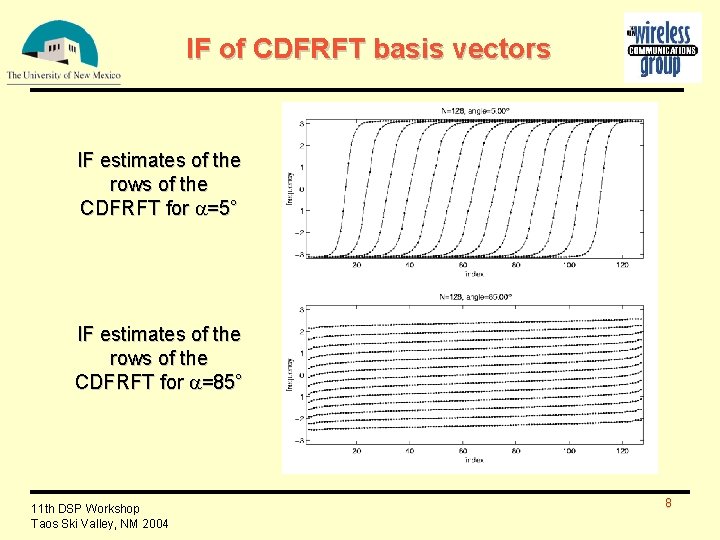
IF of CDFRFT basis vectors IF estimates of the rows of the CDFRFT for =5° IF estimates of the rows of the CDFRFT for =85° 11 th DSP Workshop Taos Ski Valley, NM 2004 8

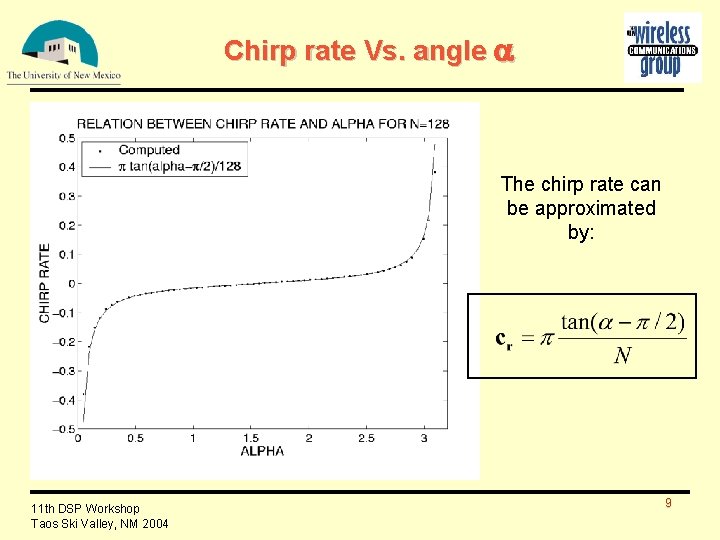
Chirp rate Vs. angle a The chirp rate can be approximated by: 11 th DSP Workshop Taos Ski Valley, NM 2004 9

Better accuracy for cr n The empirical relation: has an error slightly larger than 10%. n Restricting the angle to the range 45° to 135°: produces an error of less than 2% if we use the exact value of a at which the maximum occurs. 11 th DSP Workshop Taos Ski Valley, NM 2004 10

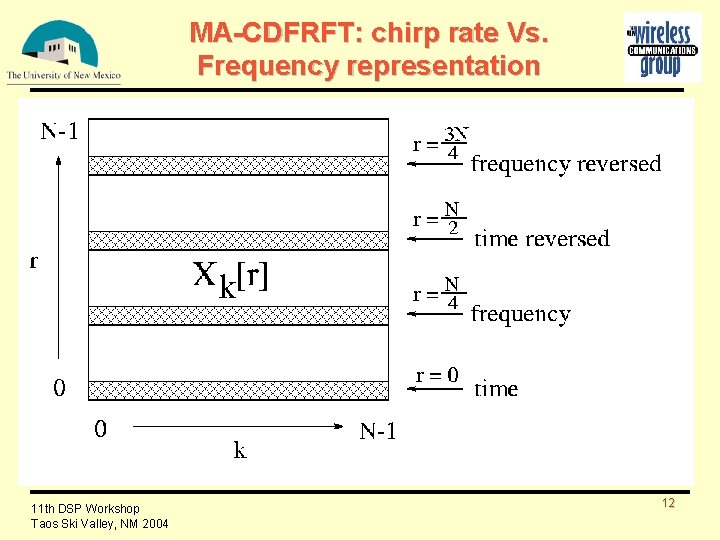
Multi-angle CDFRFT n The CDFRFT of a signal x[n] can be written as: n For the set of equally spaced angles the CDFRFT can be rewritten using index r as n Multi-angle CDFRFT (MA-CDFRFT) is a DFT & can be computed using the FFT algorithm. 11 th DSP Workshop Taos Ski Valley, NM 2004 11

MA-CDFRFT: chirp rate Vs. Frequency representation 11 th DSP Workshop Taos Ski Valley, NM 2004 12

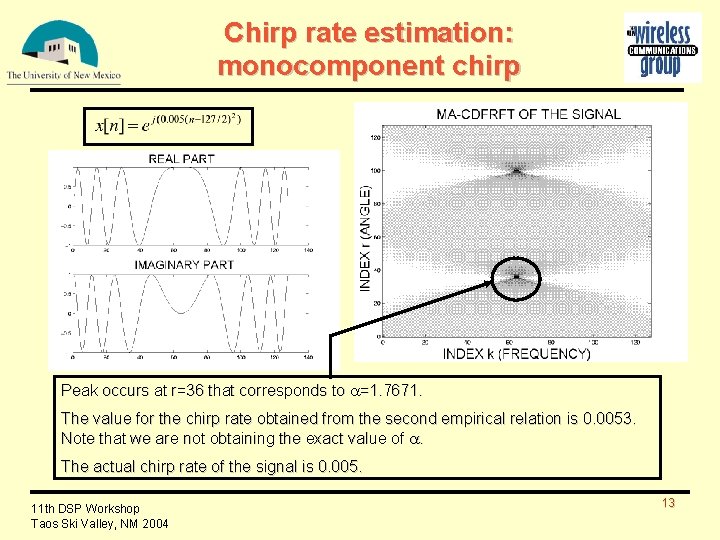
Chirp rate estimation: monocomponent chirp Peak occurs at r=36 that corresponds to =1. 7671. The value for the chirp rate obtained from the second empirical relation is 0. 0053. Note that we are not obtaining the exact value of . The actual chirp rate of the signal is 0. 005. 11 th DSP Workshop Taos Ski Valley, NM 2004 13

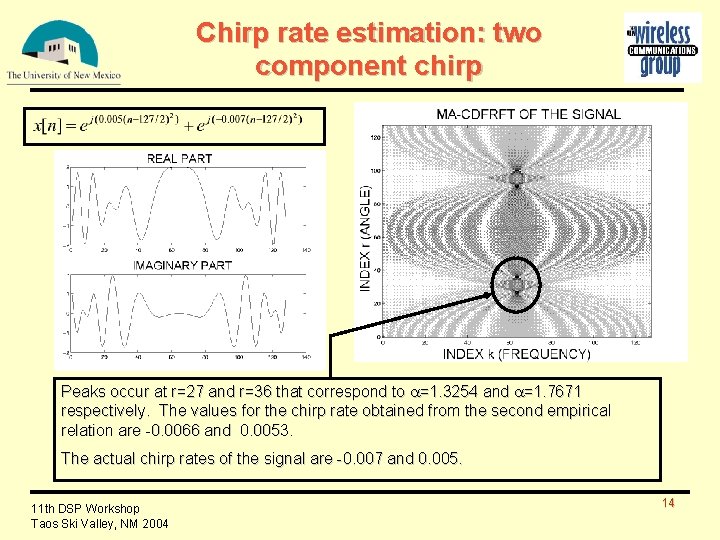
Chirp rate estimation: two component chirp Peaks occur at r=27 and r=36 that correspond to =1. 3254 and =1. 7671 respectively. The values for the chirp rate obtained from the second empirical relation are -0. 0066 and 0. 0053. The actual chirp rates of the signal are -0. 007 and 0. 005. 11 th DSP Workshop Taos Ski Valley, NM 2004 14

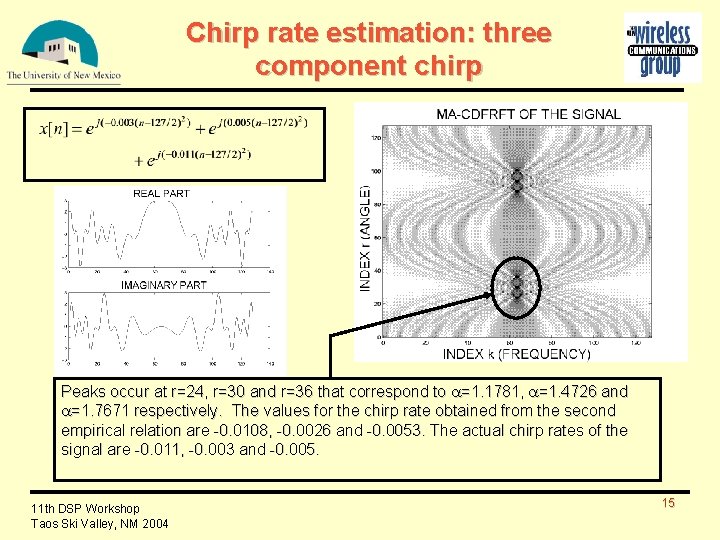
Chirp rate estimation: three component chirp Peaks occur at r=24, r=30 and r=36 that correspond to =1. 1781, =1. 4726 and =1. 7671 respectively. The values for the chirp rate obtained from the second empirical relation are -0. 0108, -0. 0026 and -0. 0053. The actual chirp rates of the signal are -0. 011, -0. 003 and -0. 005. 11 th DSP Workshop Taos Ski Valley, NM 2004 15

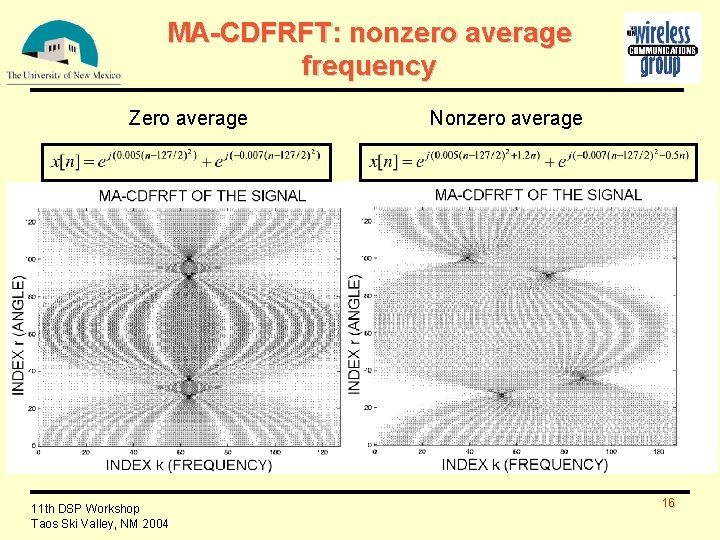
MA-CDFRFT: nonzero average frequency Zero average 11 th DSP Workshop Taos Ski Valley, NM 2004 Nonzero average 16

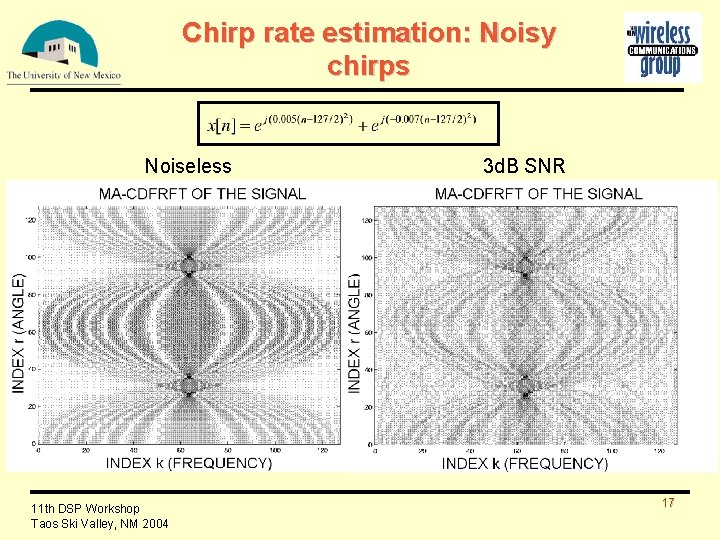
Chirp rate estimation: Noisy chirps Noiseless 11 th DSP Workshop Taos Ski Valley, NM 2004 3 d. B SNR 17

Conclusions n CDFRFT based on the Grünbaum commuting matrix can concentrate a linear chirp signal in a few coefficients. n Multiangle version of the CDFRFT can be computed efficiently using the FFT algorithm. n Empirical relations that relate the chirp rate & the angle of the CDFRFT that produces an impulse-like transform were developed. n Multi-angle CDFRFT can be applied to chirp rate estimation of mono & multicomponent signals including noisy chirps. 11 th DSP Workshop Taos Ski Valley, NM 2004 18

References n B. Santhanam and J. H. Mc. Clellan, “The Discrete Rotational Fourier Transform, ” IEEE Trans. Sig. Process. , Vol. 44, No. 4, pp. 994 -998, 1996. n S. Pei, M. Yeh, C. Tseng, “Discrete Fractional Fourier Transform Based on Orthogonal Projections, ” IEEE Trans. Sig. Process. , Vol. 47, No. 5, pp. 1335 -1348, May 1999. n C. Candan, M. A. Kutay, H. M. Ozatkas, “The Discrete Fractional Fourier Transform, ” IEEE Trans. Sig. Process. , Vol. 48, No. 5, pp. 1329 -1337, 2000. n D. H. Mugler and S. Clary, “Discrete Hermite Functions and The Fractional Fourier Transform, " in Proc. Int. Conf. Sampl. Theo. And Appl. Orlando Fl, pp. 303 -308, 2001. n S. Clary and D. H. Mugler, "Shifted Fourier Matrices and Their Tridiagonal Commutors, " SIAM Jour. Matr. Anal. & Appl. , Vol. 24, No. 3, pp. 809 -821, 2003. n B. Santhanam and J. G. Vargas-Rubio, “On the Grünbaum Commutor Based Discrete Fractional Fourier Transform, ” Proc. of ICASSP 04, Vol. II, pp. 641 -644, Montreal, 2004. n J. G. Vargas-Rubio and B. Santhanam, “Fast and Efficient Computation of a Class of Discrete Fractional Fourier Transforms, ” Submitted Sig. Process. Lett. , March 2004. 11 th DSP Workshop Taos Ski Valley, NM 2004 19