Cellular Automata Anthony Lora Outline What are Automata

Cellular Automata Anthony Lora

Outline � What are Automata? � Von Neuman’s Machine � A Simple CA � CA ? = TM � Features � Examples

What is an Automaton? �A self-operating machine or mechanism � Automata Theory: ◦ Study of abstract, mathematical machines and systems. ◦ Includes: • • • Deterministic Finite Automata (DFA) Nondeterministic Finite Automata (NFA) Pushdown Automata (PDA) Turing Machines (TM) Cellular Automata (CA)

Cellular Automata � Proposed by John von Neumann in the late 1940 s to model self-reproducing organisms � If a machine were surrounded by “hardware soup, ” could it create a working copy of itself? ◦ Possible if the machine had a blueprint for itself ◦ Make a copy of the blueprint and use it as instructions for building � Stanislaw Ulam suggested using cells to represent the parts

A Simple CA � One-dimensional array of cells � Each cell has a state � Time is divided into discrete units � A function (the “local rule”) determines how cell state changes ◦ State change determined by the cell’s state and the state of its two neighbors � At each clock tick, the local rule is run on the cells in parallel

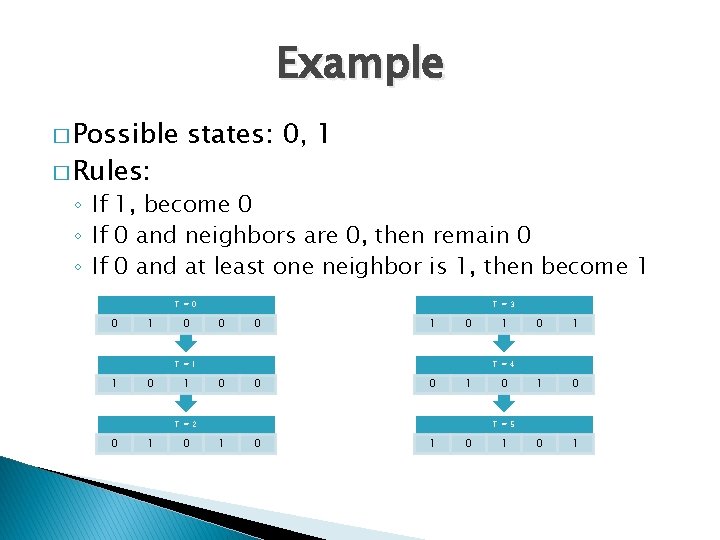
Example � Possible � Rules: states: 0, 1 ◦ If 1, become 0 ◦ If 0 and neighbors are 0, then remain 0 ◦ If 0 and at least one neighbor is 1, then become 1 T=0 0 1 0 T=3 0 0 1 0 T=1 1 0 0 1 T=4 0 0 0 1 T=2 0 1 0 T=5 1 0 1

Self-Reproducing Automata § § Von Neumann’s CA had cells capable of 29 different states, though it has been simplified since then. Had to be capable of universal computation in order to be nontrivial ◦ AKA – Turing-complete, or capable of simulating a single-tape Turing machine

Turing Machine 101 � Four Parts ◦ Tape - Two-way infinite, divided into cells, each one holding a symbol from a finite set ◦ Head - Can read symbols, move left and right one cell, and update cell contents ◦ State Register – Holds the state of the machine ◦ Table – Holds the different instructions for the TM, based on the symbol read and the state �Update cell contents, if necessary �Move left or right, if necessary �Change state, if necessary

From TM to CA § The state of the cells has two components ◦ Tape symbol from the equivalent TM ◦ Whether the TM’s head is scanning the present cell § Rule 1: ◦ If the head is not scanning the cell, or either of its neighbors, the cell contents remain the same T=0 … 0/A 0/B 0/C … T=1 … 0/A 0/B

From TM to CA � Rule 2: ◦ If the head is scanning the right cell and there is a left move, then the current cell will be scanned in the next step. Same goes for a left cell and right move. ◦ Example: At A, shift right. T=0 … 1/A 0/B 0/C … T=1 … 0/A 1/B

From TM to CA � Rule 3: ◦ If the present cell is being scanned, change contents according to TM’s rules and stop scanning the cell, if necessary. ◦ Rule: At C, update to Z and shift left. T=0 … 0/A 0/B 1/C … 0/Z … T=1 … 0/A 1/B

Features of a CA � Cell States ◦ Set of all possible states must be finite ◦ Usually exists a quiescent state ◦ Polygeneous CA - Has cells whose states come from different sets � Geometry ◦ Can be a d-dimensional grid ◦ Can be finite or infinite in any direction

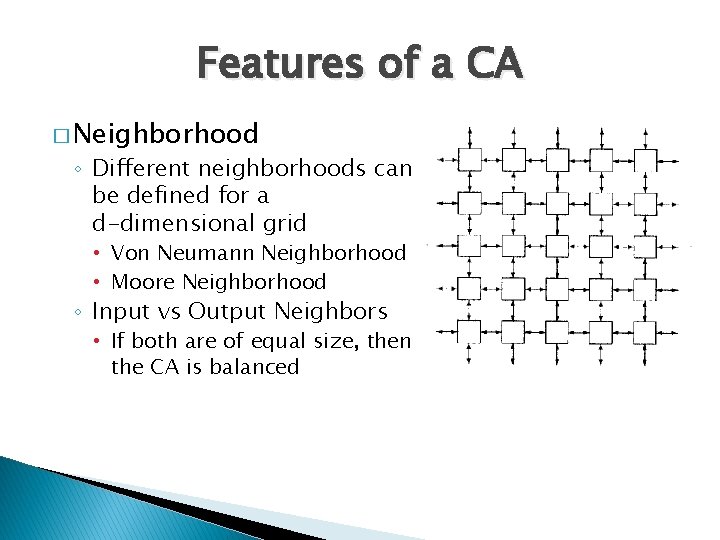
Features of a CA � Neighborhood ◦ Different neighborhoods can be defined for a d-dimensional grid • Von Neumann Neighborhood • Moore Neighborhood ◦ Input vs Output Neighbors • If both are of equal size, then the CA is balanced

Features of a CA � Local Rules ◦ Hybrid CA – Each cell has its own local rules ◦ Possible for cells to change their local rule at each time step

Conway’s Game of Life Made by John Horton Conway in 1970 ◦ Design a simple set of rules to model a population Setup ◦ States: 0 (non-living), 1 (living) ◦ 2 -dimensional with a Moore neighborhood ◦ Rules: • Survival – If alive and has 2 or 3 living neighbors, then remains alive • Birth – If non-living and has exactly 3 living neighbors, then becomes alive • Death – If alive, becomes non-living if it has 0 or 1 living neighbors or 4+ living neighbors • The Game of Life

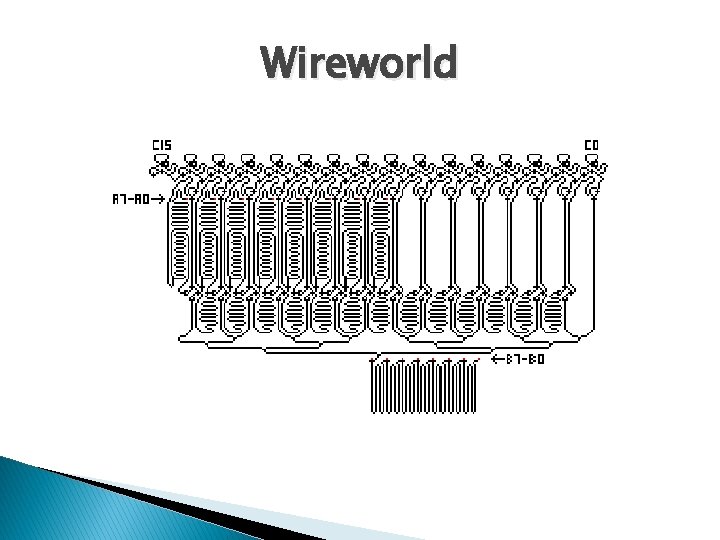
Wireworld � Introduced by Brian Silverman in 1987 as part of Phantom Fish Tank program ◦ Uses four color states, a 2 -D grid, and Moore neighborhood ◦ Rules �Color 0 is background always stays that way �Color 1 is an electron head and always becomes a tail �Color 2 is an electron tail and always turns into wire �Color 3 is wire, which remains wire unless 1 or 2 of the neighboring cells are electron heads, in which case it becomes an electron head as well

Wireworld � Can simulate digital logic circuits ◦ 2002 – Nick Gardner demonstrates how Wireworld can be used to multiply two 8 -bit numbers ◦ A computer that can count off prime numbers has also been created

Wireworld

Elementary CA � Introduced by Stephen Wolfram in 1983 � Two states, 1 -D, left and right neighbors � Below is the set of rules for Rule 165 � Total of 256 elementary CA

Elementary CA � Often depicted a single black cell in the center for initial conditions � Rule 165:

Rule 110 � Capable of universal computation � Mirror: Rule 124, Compliment: 137, Both: 193

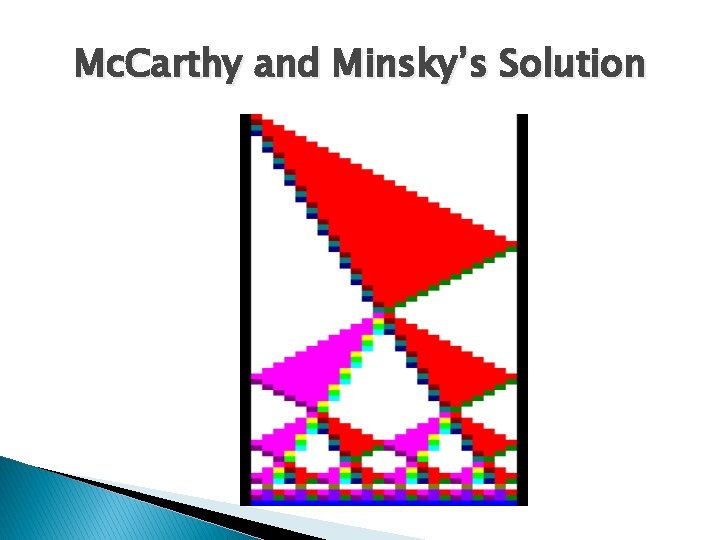
Firing Squad Problem � Proposed by John Myhill in 1957 � Solved by John Mc. Carthy and Marvin Minsky and published in 1962 by Edward Moore � Problem: ◦ A line of N soldiers stand in the idle state ◦ Soldier on the far left (the general) gives the signal to fire ◦ Soldiers can only communicate with their left and right neighbors ◦ All soldiers must fire only once and at the same time

Firing Squad Problem � Original solution takes 15 states and works in 3 N time � Most optimal time is 2 N-2 and takes thousands of states � A 6 -state solution exists and a 4 -state solution is impossible � Unknown whether a 5 -state solution may exist

Mc. Carthy and Minsky’s Solution

Resources � “A Brief History of Cellular Automata” by Palash Sarkar � “Cellular Automata Laboratory” by Rudy Rucker and John Walker � Wolfrom Math. World