Cell Cycle Control at the First Restriction Point

Cell Cycle Control at the First Restriction Point and its Effect on Tissue Growth Joint work with Avner Friedman and Bei Hu (MBI, The Ohio State University and Notre Dame University) Chiu-Yen Kao 高秋燕

Outline of the Talk 1. What is cell cycle? 2. Two restriction points (check points). 3. Mathematical Model: System of PDEs 4. Theorems 5. Numerical Demonstrations 2

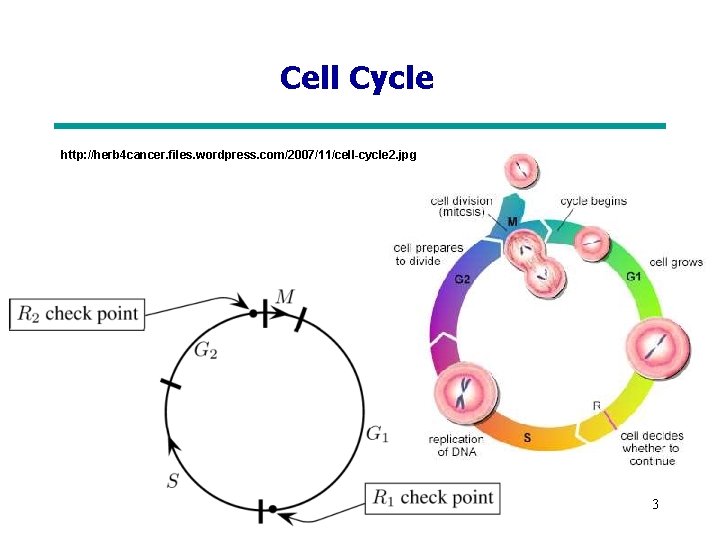
Cell Cycle http: //herb 4 cancer. files. wordpress. com/2007/11/cell-cycle 2. jpg 3

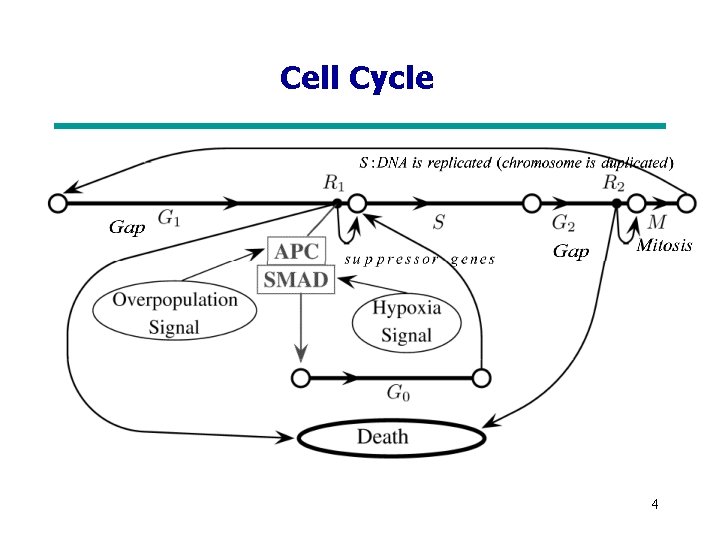
Cell Cycle 4

Mathematical Model: Equations 5

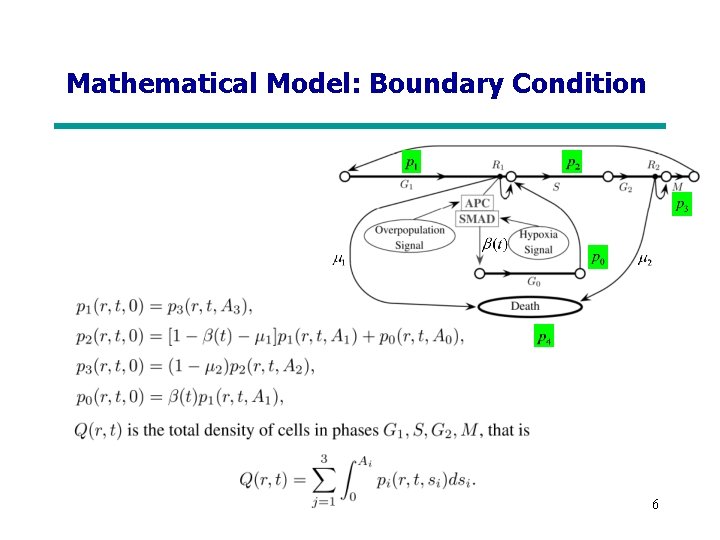
Mathematical Model: Boundary Condition 6

Control at the First Restriction Point 7

Conservation of Total Density 8

Radial Symmetric Velocity Oxygen Concentration 9

Boundary Conditions & Initial Conditions The global existence and uniqueness for radially symmetric solutions is established by A. Friedman Remark: We assume the oxygen level is above the necrotic level and growth rate and death rate are independent of oxygen concentration. 10

Check point Control : constant case 11

Check point Control : constant case 12

Check point Control : constant case 13

Check point Control : constant case Idea: obtain a delay equation for Q 14

Check point Control : constant case 15

Check point Control : constant case 16

Check point Control : constant case 17

Check point Control : constant case Idea: lower bound & upper bound 0 0 18

Check point Control : constant case Similarly, 19

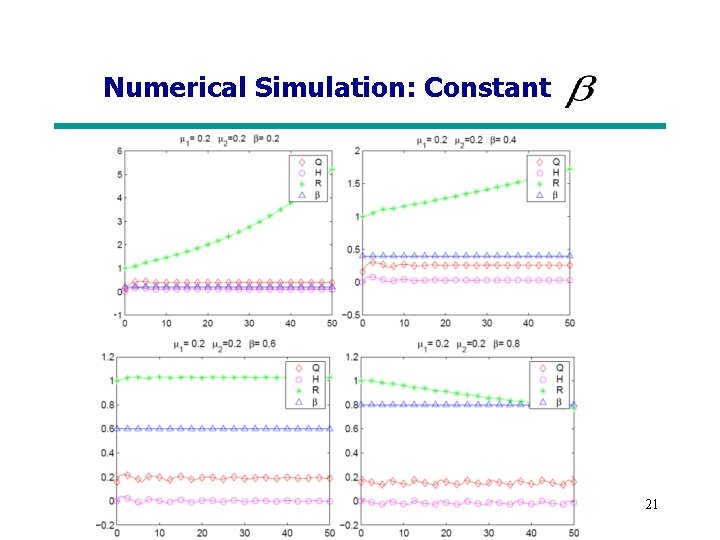
Numerical Simulation: Constant 20

Numerical Simulation: Constant 21

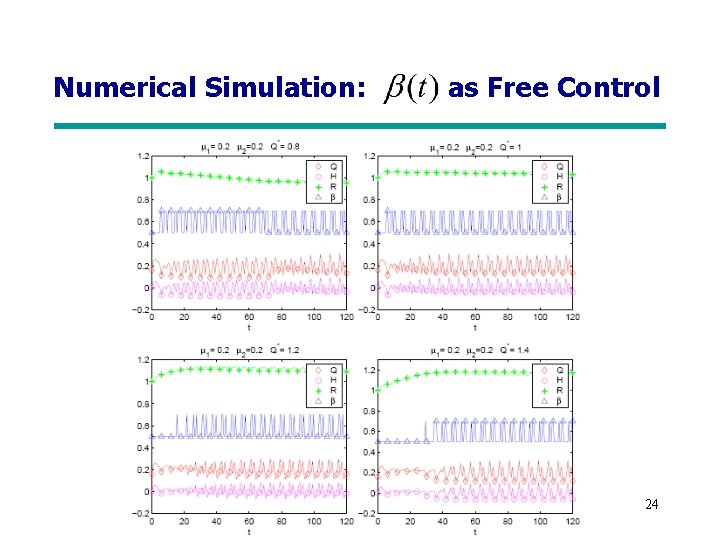
as Free Control 22

as Free Control Idea: Mathematical Induction Thus 23

Numerical Simulation: as Free Control 24

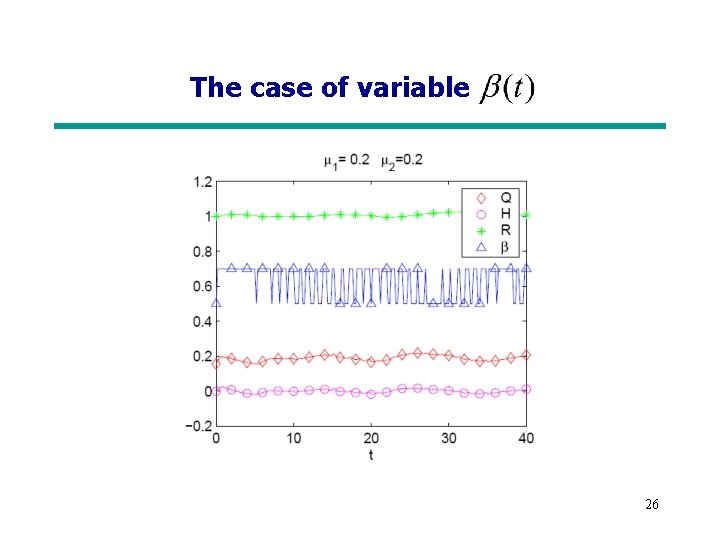
The case of variable 25

The case of variable 26

Conclusion Ø A multiscale model with two time scales: the usual time, t, and the running time of cells in each phase of the cell cycle. Ø The growth or shrinkage of a tissue depends on a decision that individual cells make whether to proceed directly from the first restriction point to the S phase or whether to go first into quiescent state. Ø The radius can be controlled by. With suitable radius is bounded above and below for all time. Ø The model can be easily extended to two (or more) populations of cells. (ex. healthy cell and tumor cell) , the 27

Selected References 28

The End 29