CEE 320 Fall 2008 Queuing CEE 320 Anne

CEE 320 Fall 2008 Queuing CEE 320 Anne Goodchild

Outline 1. 2. 3. 4. 5. Fundamentals Poisson Distribution Notation Applications Analysis a. Graphical b. Numerical CEE 320 Fall 2008 6. Example

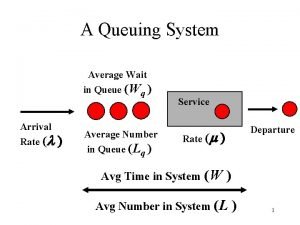
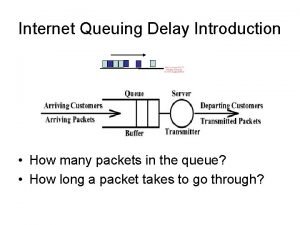
Fundamentals of Queuing Theory • Microscopic traffic flow – Different analysis than theory of traffic flow – Intervals between vehicles is important – Rate of arrivals is important CEE 320 Fall 2008 • Arrivals • Departures • Service rate

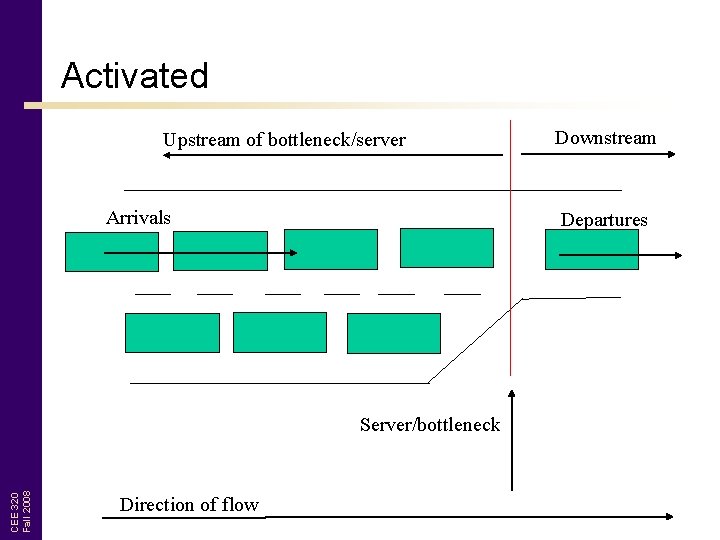
Activated Upstream of bottleneck/server Arrivals Departures CEE 320 Fall 2008 Server/bottleneck Direction of flow Downstream

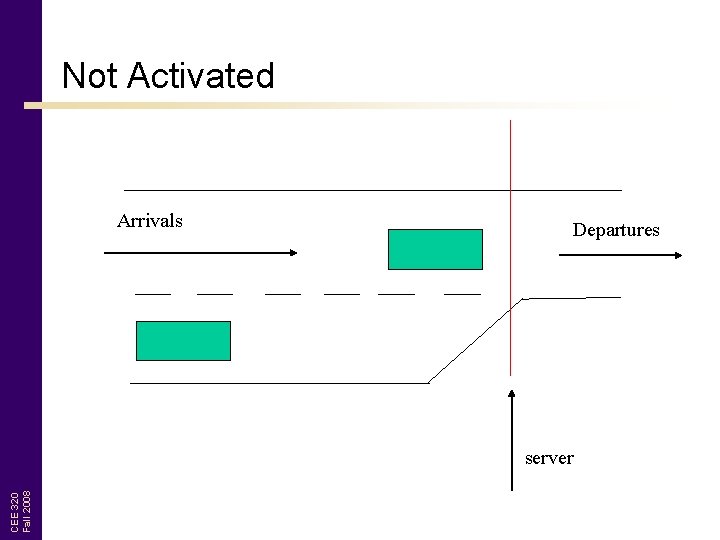
Not Activated Arrivals Departures CEE 320 Fall 2008 server

Flow Analysis • Bottleneck active CEE 320 Fall 2008 – Service rate is capacity – Downstream flow is determined by bottleneck service rate – Arrival rate > departure rate – Queue present

Flow Analysis • Bottle neck not active CEE 320 Fall 2008 – – Arrival rate < departure rate No queue present Service rate = arrival rate Downstream flow equals upstream flow

CEE 320 Fall 2008 • http: //trafficlab. ce. gatech. edu/freewayapp/ Road. Applet. html

Fundamentals of Queuing Theory • Arrivals – Arrival rate (veh/sec) • Uniform • Poisson – Time between arrivals (sec) • Constant • Negative exponential • Service CEE 320 Fall 2008 – Service rate – Service times • Constant • Negative exponential

Queue Discipline • First In First Out (FIFO) – prevalent in traffic engineering CEE 320 Fall 2008 • Last In First Out (LIFO)

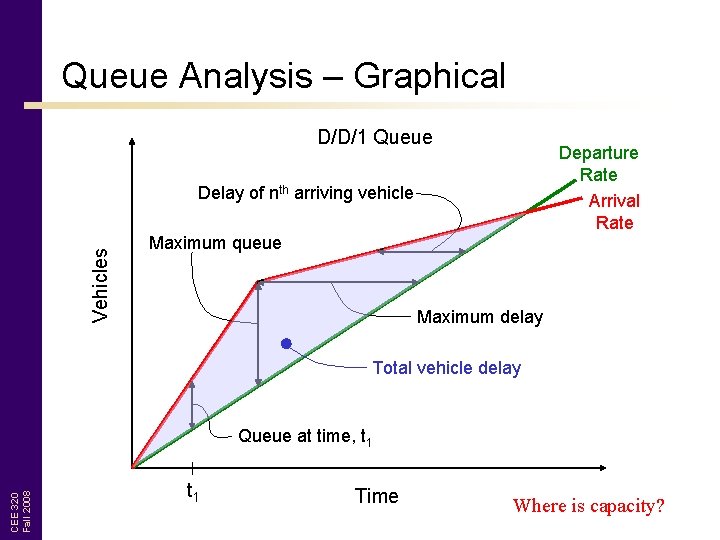
Queue Analysis – Graphical D/D/1 Queue Departure Rate Arrival Rate Vehicles Delay of nth arriving vehicle Maximum queue Maximum delay Total vehicle delay CEE 320 Fall 2008 Queue at time, t 1 Time Where is capacity?

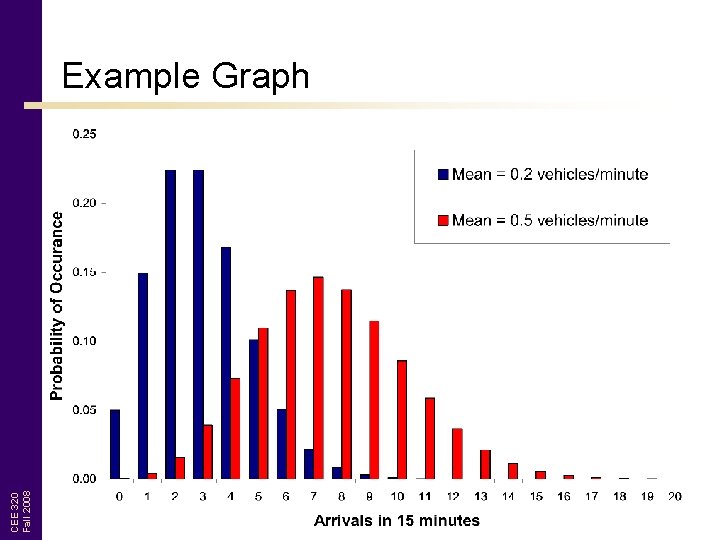
Poisson Distribution • Good for modeling random events • Count distribution – Uses discrete values – Different than a continuous distribution P(n) = probability of exactly n vehicles arriving over time t n = number of vehicles arriving over time t CEE 320 Fall 2008 λ = average arrival rate t = duration of time over which vehicles are counted

Poisson Ideas • Probability of exactly 4 vehicles arriving – P(n=4) • Probability of less than 4 vehicles arriving – P(n<4) = P(0) + P(1) + P(2) + P(3) • Probability of 4 or more vehicles arriving – P(n≥ 4) = 1 – P(n<4) = 1 - P(0) + P(1) + P(2) + P(3) CEE 320 Fall 2008 • Amount of time between arrival of successive vehicles

CEE 320 Fall 2008 Example Graph

CEE 320 Fall 2008 Example Graph

CEE 320 Fall 2008 Example: Arrival Intervals

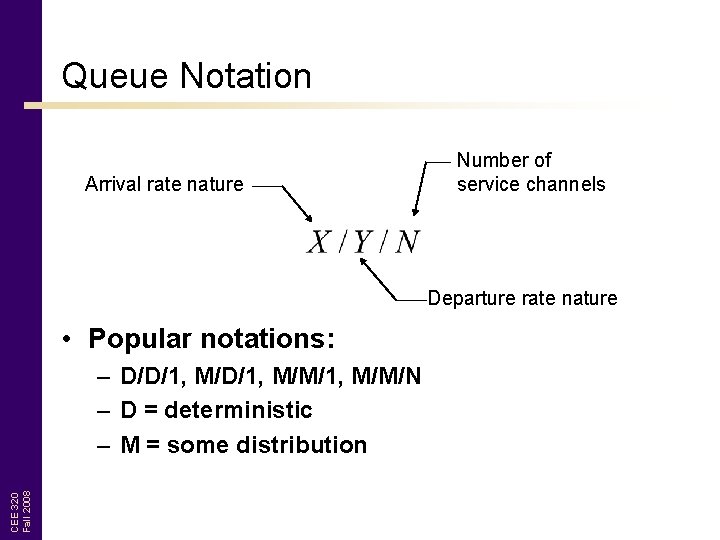
Queue Notation Arrival rate nature Number of service channels Departure rate nature • Popular notations: CEE 320 Fall 2008 – D/D/1, M/M/1, M/M/N – D = deterministic – M = some distribution

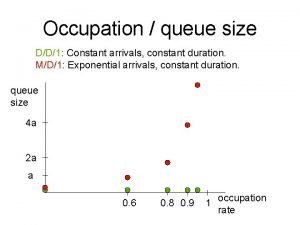
Queuing Theory Applications • D/D/1 – Deterministic arrival rate and service times – Not typically observed in real applications but reasonable for approximations • M/D/1 – General arrival rate, but service times deterministic – Relevant for many applications • M/M/1 or M/M/N CEE 320 Fall 2008 – General case for 1 or many servers

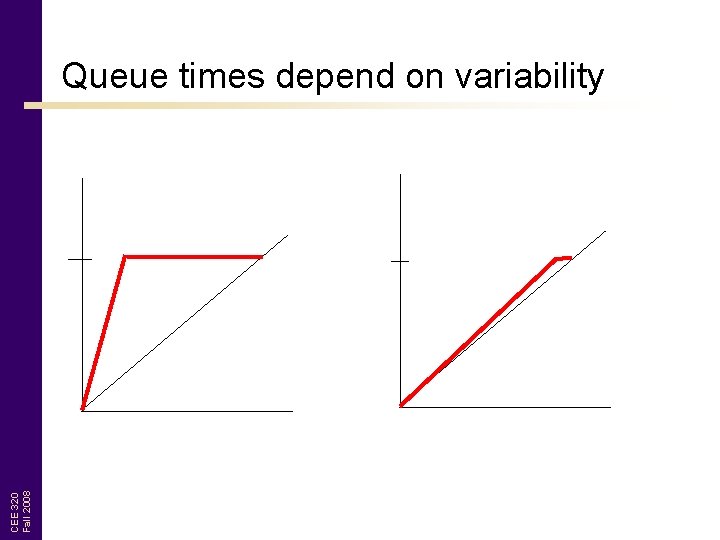
CEE 320 Fall 2008 Queue times depend on variability

Steady state assumption Queue Analysis – Numerical • M/D/1 – Average length of queue – Average time waiting in queue CEE 320 Fall 2008 – Average time spent in system λ = arrival rate μ = departure rate =traffic intensity

Queue Analysis – Numerical • M/M/1 – Average length of queue – Average time waiting in queue CEE 320 Fall 2008 – Average time spent in system λ = arrival rate μ = departure rate =traffic intensity

Queue Analysis – Numerical • M/M/N – Average length of queue – Average time waiting in queue CEE 320 Fall 2008 – Average time spent in system λ = arrival rate μ = departure rate =traffic intensity

M/M/N – More Stuff – Probability of having no vehicles – Probability of having n vehicles CEE 320 Fall 2008 – Probability of being in a queue λ = arrival rate μ = departure rate =traffic intensity

Poisson Distribution Example Vehicle arrivals at the Olympic National Park main gate are assumed Poisson distributed with an average arrival rate of 1 vehicle every 5 minutes. What is the probability of the following: CEE 320 Fall 2008 1. Exactly 2 vehicles arrive in a 15 minute interval? 2. Less than 2 vehicles arrive in a 15 minute interval? 3. More than 2 vehicles arrive in a 15 minute interval? From HCM 2000

Example Calculations Exactly 2: Less than 2: P(0)=e-. 2*15=0. 0498, P(1)=0. 1494 CEE 320 Fall 2008 More than 2:

Example 1 You are entering Bank of America Arena at Hec Edmunson Pavilion to watch a basketball game. There is only one ticket line to purchase tickets. Each ticket purchase takes an average of 18 seconds. The average arrival rate is 3 persons/minute. CEE 320 Fall 2008 Find the average length of queue and average waiting time in queue assuming M/M/1 queuing.

Example 1 • Departure rate: μ = 18 seconds/person or 3. 33 persons/minute • Arrival rate: λ = 3 persons/minute • ρ = 3/3. 33 = 0. 90 • Q-bar = 0. 902/(1 -0. 90) = 8. 1 people • W-bar = 3/3. 33(3. 33 -3) = 2. 73 minutes CEE 320 Fall 2008 • T-bar = 1/(3. 33 – 3) = 3. 03 minutes

Example 2 You are now in line to get into the Arena. There are 3 operating turnstiles with one ticket-taker each. On average it takes 3 seconds for a ticket-taker to process your ticket and allow entry. The average arrival rate is 40 persons/minute. CEE 320 Fall 2008 Find the average length of queue, average waiting time in queue assuming M/M/N queuing.

CEE 320 Fall 2008 Example 2 • • • N=3 Departure rate: μ = 3 seconds/person or 20 persons/minute Arrival rate: λ = 40 persons/minute ρ = 40/20 = 2. 0 ρ/N = 2. 0/3 = 0. 667 < 1 so we can use the other equations • • P 0 = 1/(20/0! + 21/1! + 22/2! + 23/3!(1 -2/3)) = 0. 1111 Q-bar = (0. 1111)(24)/(3!*3)*(1/(1 – 2/3)2) = 0. 88 people T-bar = (2 + 0. 88)/40 = 0. 072 minutes = 4. 32 seconds W-bar = 0. 072 – 1/20 = 0. 022 minutes = 1. 32 seconds

Example 3 You are now inside the Arena. They are passing out Harry the Husky doggy bags as a free giveaway. There is only one person passing these out and a line has formed behind her. It takes her exactly 6 seconds to hand out a doggy bag and the arrival rate averages 9 people/minute. CEE 320 Fall 2008 Find the average length of queue, average waiting time in queue, and average time spent in the system assuming M/D/1 queuing.

Example 3 • N=1 • Departure rate: μ = 6 seconds/person or 10 persons/minute • Arrival rate: λ = 9 persons/minute • ρ = 9/10 = 0. 9 CEE 320 Fall 2008 • Q-bar = (0. 9)2/(2(1 – 0. 9)) = 4. 05 people • W-bar = 0. 9/(2(10)(1 – 0. 9)) = 0. 45 minutes = 27 seconds • T-bar = (2 – 0. 9)/((2(10)(1 – 0. 9) = 0. 55 minutes = 33 seconds

CEE 320 Fall 2008 Primary References • Mannering, F. L. ; Kilareski, W. P. and Washburn, S. S. (2003). Principles of Highway Engineering and Traffic Analysis, Third Edition (Draft). Chapter 5 • Transportation Research Board. (2000). Highway Capacity Manual 2000. National Research Council, Washington, D. C.