Ce compartiment am nceput sl studiem acum la





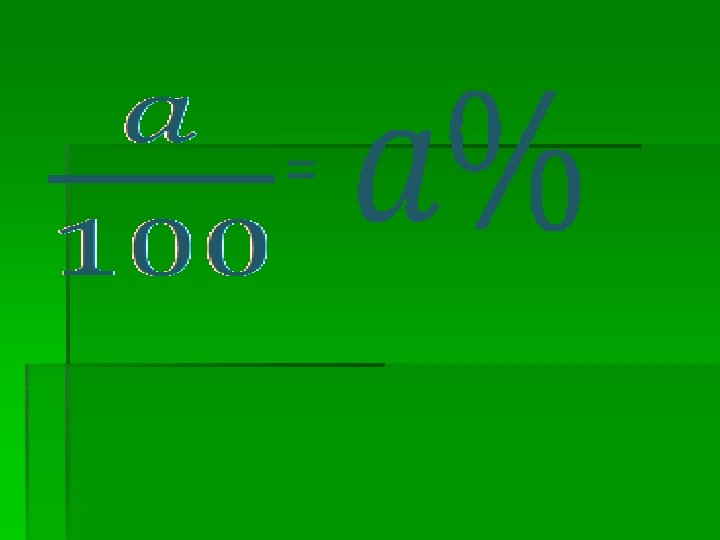

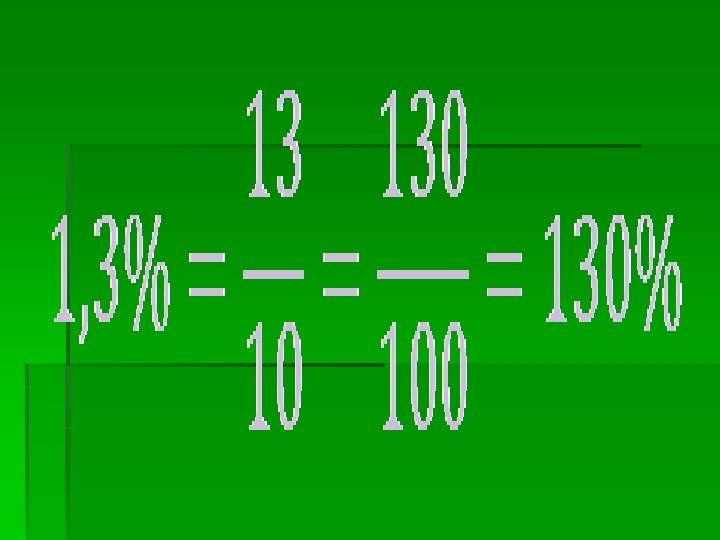











- Slides: 20

Ce compartiment am început să-l studiem acum la matematică ?

Rapoarte şi proporţii. Daţi exemple de cîteva rapoarte.

-rapoarte

Ce raport este scris mai jos ?

Răspuns: Raport procentual. Cu ce este egal raportul procentual?
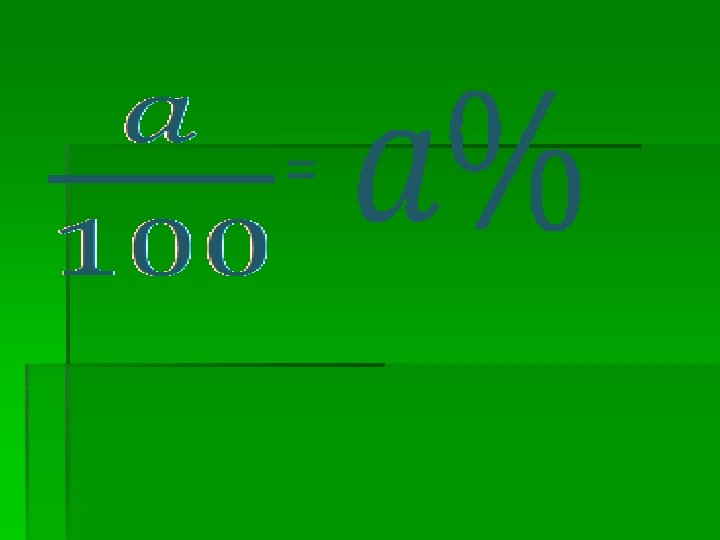

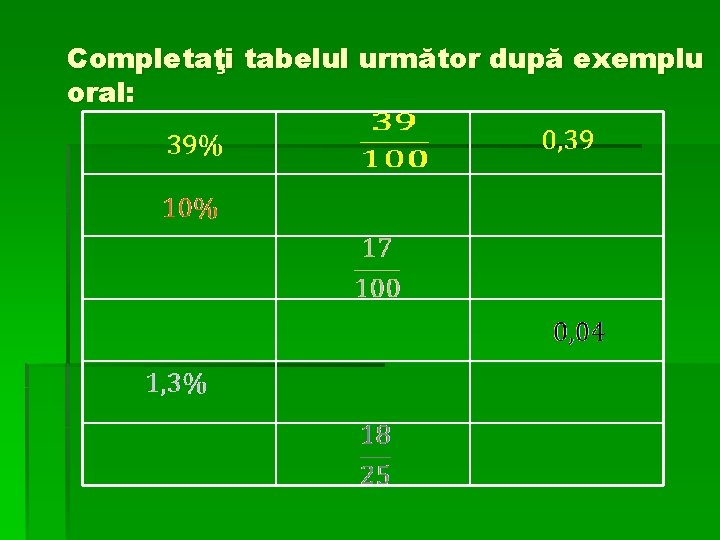
Completaţi tabelul următor după exemplu oral:

Cum aţi procedat la exemplul 1, 3 % ?
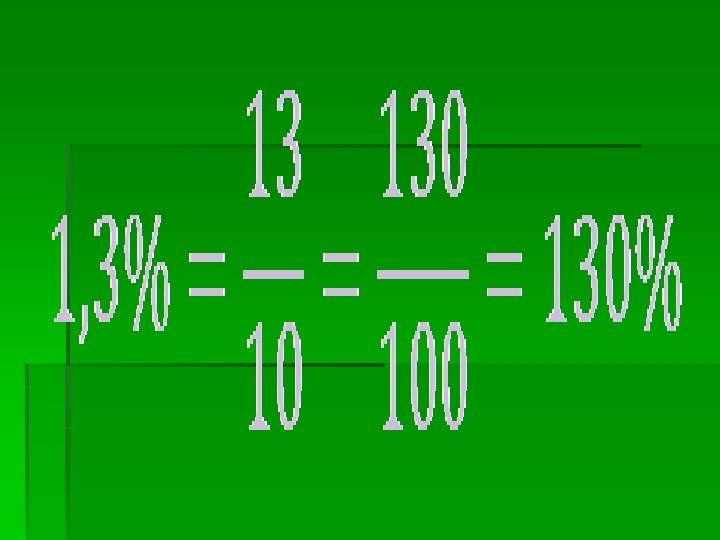

În viaţa de zi cu zi întîlnim o serie întregă de fapte care pot fi caracterizate prin numere asociate unor mărimi. § Astfel, dacă mergem la cumpărături, suntem nevoiţi să plătim marfa pe care o cumpărăm. Avem deci ca mărime-cantitatea de marfă cumpărată şi preţul acesteia. § Dacă ne deplesăm de la domiciliu la şcoală sau către locul de muncă avem de parcurs o distanţă, în diferite moduri (mai rapid sau mai lent, în funcţie de mijlocul de transport utilizat). § Prin urmare, timpul necesar parcurgerii distanţei respective depinde de viteza cu care ne deplasăm. § Dacă avem de împărţit o sumă de bani la mai multe persoane, în mod egal, atunci suma cei revine fiecărei persoane depinde de numărul de persoane.

Cum credeţi ce temă vom studia azi la lecţie ?

Subiectul orei: Mărimi direct proporţionale. Mărimi invers proporţionale. Regula de trei simplă.

Obiectivele orei: § O 1 Să definească, identifice rapoarte şi proporţii direct şi invers proporţionale; § O 2 Să definească mărimile direct proporţionale şi invers proporţionale § O 3 Să rezolve probleme în care intervin relaţii de proporţionalitate directă, şi indirectă; § O 4 să reprezinte prin tabele, grafice variaţia unei mărimi dependente de timp; § O 5 Justificarea unui rezultat sau demers simplu, susţinerea propriilor idei şi viziuni, recurgînd la argumentări, utilizînd terminologia şi notaţiile adecvate.

1. Mărimi direct proporţionale. Din exemplele de mai sus reţinem că mărimile asociate unor evenimente, fenomene, depind unele de altele. Definiţie: Două mărimi care depind una de alta astref încît dacă una creşte (descreşte) de un număr de ori, atunci şi cealaltă creşte(descreşte) de acelaşi număr de ori, se numesc mărimi direct proporţionale. Exemplu: Preţul unui caiet este de 2 lei. Cît va costa 2 caiete, dar 42 caiete 3? Nr. caiete 1 4 Preţ(lei) 2 4 6 8

Dacă vom reprezenta într-un sistem de axe perechile de numere din tabelul de mai sus, vom obţine o imagine a modulului cum depinde preţul de numărul de caiete cumpărate. § Se observă faptul că dacă numărul de caiete cumpărate creşte, de exemplu , de două ori, preţul creşte tot de două ori, sau dacă numărul caietelor cumpărate este de 4 ori mare, atunci vom plăti de 4 ori mai mult. Dacă vom uni punctele corespunzătoare perechilor de valori obţinute, vom obţine o linie dreaptă. Dreapta obţinută este graficul acestei dependenţe.

2. Mărimi invers proporţionale. § Definiţie: Două mărimi care depind una de alta, astfel încît dacă una creşte (descreşte) de un număr de ori, atunci cealaltă descreşte(creşte) de acelaşi număr de ori, se numesc mărimi invers proporţionale. Exemplu: Radu şi Ion sunt vecini, au aceeaşi vîrstă, dar învaţă în şcoli diferite. SAmbii fiind pasionaţi de ciclism, au participat la competiţiile orăşeneşti, fiecare în echipa şcolii sale. Iată rezultatele obţinute de cei doi prieteni. Radu Ion V(km/h) 50 40 T(h) 1, 2 1, 5 Reţinem: Dacă viteza se măreşte, atunci timpul descreşte.

3. Regula de trei simplă (în cazul mărimilor direct proporţionale) § Un automobilist a parcurs distanţa de 200 km în 2, 5 h. În cît timp va parcurge el o distanţă de 320 km, dacă mişcarea lui este uniformă? Rezolvare Putem organiza datele întrun schemă: 2, 5 h. . . . 200 km x h. . . . 320 km deci

4. Regula de trei simplă (în cazul mărimilor invers proporţionale) § Două tractoare ară o suprafaţă în 10 h. În cît timp vor ara aceeaşi suprafaţă 7 tractoare ? Rezolvare Organizăm datele în următoarea achemă: 7 tractoare. . x h 2 tractoare. . 10 h Deoarece avem mărimi invers proporţionale, obţinem:

Fişă de lucru Marimi direct proporţionale. Marimi invers proporţionale. Regula de trei simpla 1. Notati in paranteza care din urmatoarele perechi de marimi sunt direct proporţionale si care invers proporţionale : a)numărul de caiete si pretul lor (……………) b)numărul de robinete cu acelasi debit si timpul in care ele umplu un bazin (……………) c)lungimea laturii unui patrat si perimetrul lui (……………. ) 3. Completaţi tabelul următor ştiind că x si y sunt mărimi direct proporţionale: x y 2 4 20 6 12 40 50 14 80 Timp de lucru: 15 minute 2. ştiind că 3 kg de mere costă 6 lei calculaţi cît costă 7 kg de mere. …………………………………………………………………………………………. . 4. ştiind că 4 tractoare ară un teren in 10 h aflaţi în cîte ore ară acelaşi teren 5 tractoare. …………………………………………………………………………………………. .

Realizat: Profesor Carajia Elena, grad didactic II gimnaziul Sărățica Nouă Clasa a VI-a