CE 424 HYDROLOGY Chapter 6 Hydrograph Analysis Dr

CE 424 HYDROLOGY Chapter 6 Hydrograph Analysis Dr. Saleh Al. Hassoun 1

Hydrograph Record of River Discharge over a period of time ; Q vs t River Discharge : Q = AXv = cross sectional area X rivers mean (average) velocity (at a particular point in its course) Storm Hydrographs Show the change in discharge caused by a period of rainfall

Why Construct & Analyse Hydrographs ? To find out discharge patterns of a particular drainage basin Help predict flooding events, therefore influence implementation of flood prevention measures ©Microsoft Word clipart

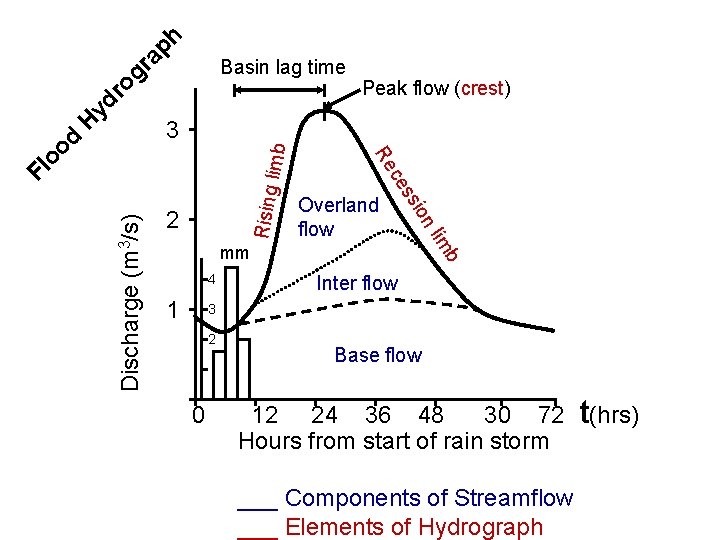
ph yd ro gr a Basin lag time Peak flow (crest) limb Discharge Rising (m 3/s) Fl o mm 4 1 b im nl sio Overland flow s ce 2 Re od H 3 Inter flow 3 2 0 Base flow 12 24 36 48 30 72 Hours from start of rain storm ___ Components of Streamflow ___ Elements of Hydrograph t(hrs)

Discharge (m 3/s) 3 2 1 0 12 24 36 48 30 Hours from start of rain storm 72

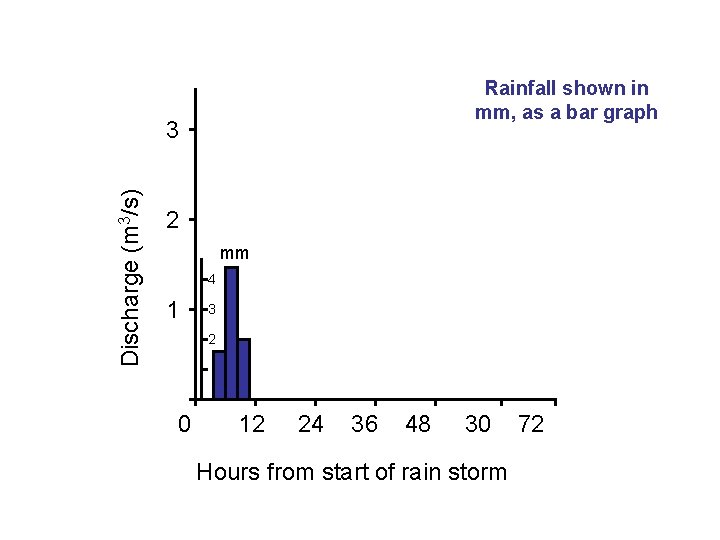
Rainfall shown in mm, as a bar graph Discharge (m 3/s) 3 2 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

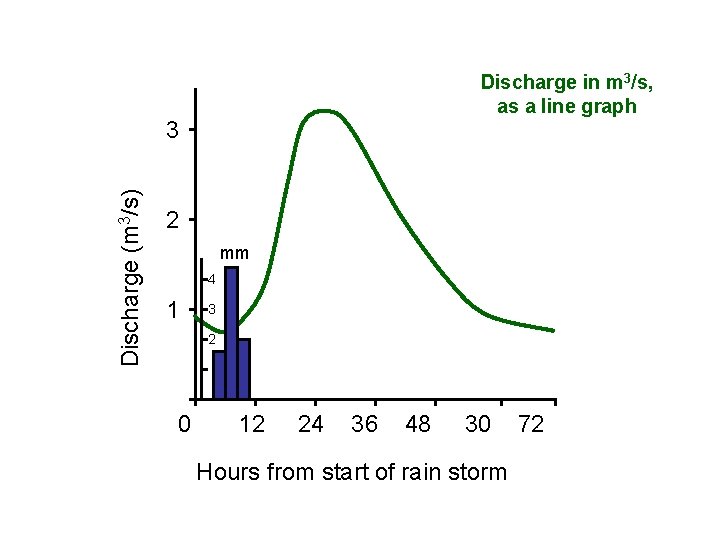
Discharge in m 3/s, as a line graph Discharge (m 3/s) 3 2 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

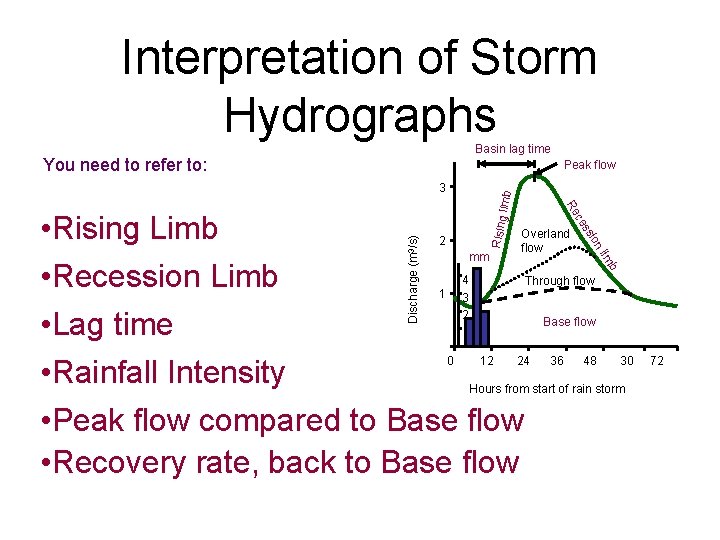
Rising limb The rising flood water in the river Rising Discharge (m 3/s) limb 3 2 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

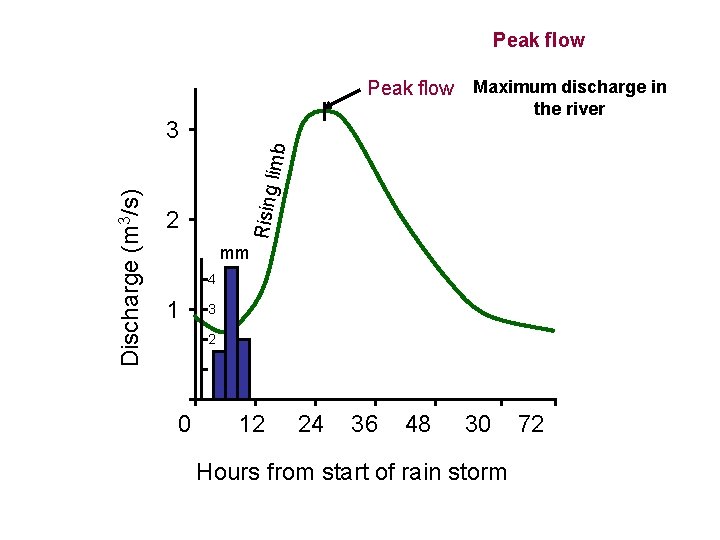
Peak flow Maximum discharge in the river Rising Discharge (m 3/s) limb 3 2 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

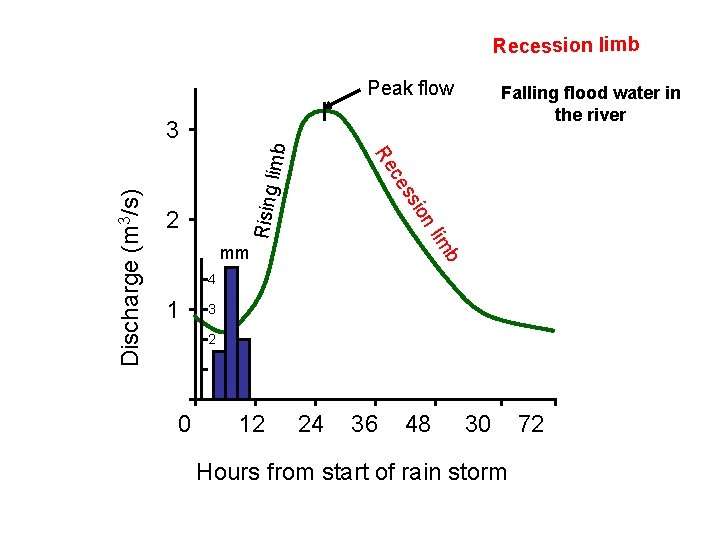
Recession limb Peak flow Falling flood water in the river Rising b im nl 2 sio Discharge (m 3/s) s ce Re limb 3 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

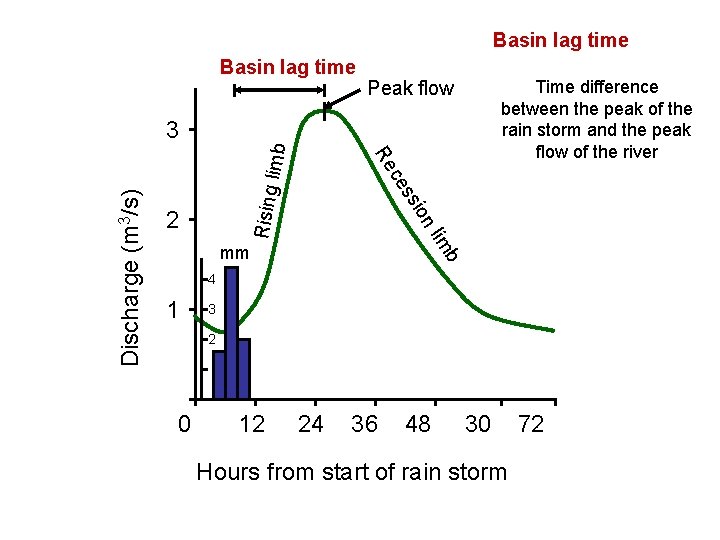
Basin lag time Time difference between the peak of the rain storm and the peak flow of the river Peak flow Rising b im nl 2 sio Discharge (m 3/s) s ce Re limb 3 mm 4 1 3 2 0 12 24 36 48 30 Hours from start of rain storm 72

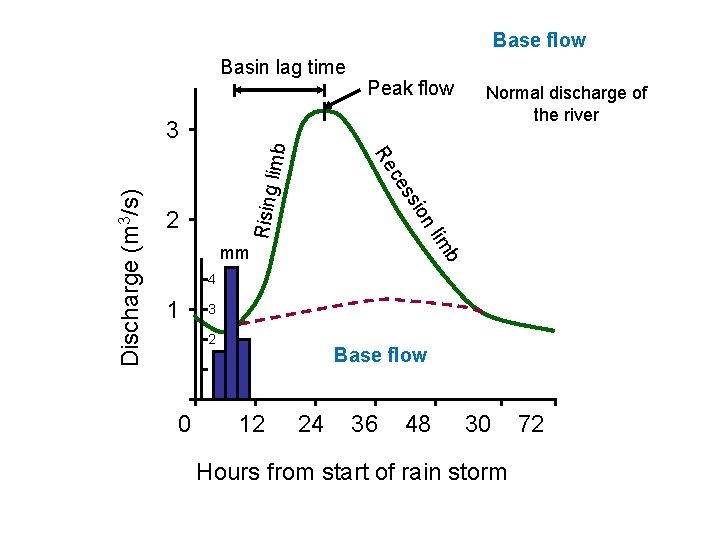
Base flow Basin lag time Peak flow Rising b im nl 2 sio Discharge (m 3/s) s ce Re limb 3 Normal discharge of the river mm 4 1 3 2 0 Base flow 12 24 36 48 30 Hours from start of rain storm 72

Overland flow Basin lag time + Peak flow Inter flow + Rising Discharge (m 3/s) b im 1 Inter flow 3 2 0 Stream Flow Or Total Runoff nl mm 4 = sio Overland flow s ce 2 GW (BF) Re limb 3 Base flow 12 24 36 48 30 Hours from start of rain storm 72

Overland flow Volume of water reaching the river from surface run off GW The Base flow Inter flow Volume of water reaching the river through the soil and underlying rock layers

Factors influencing Storm Hydrographs • Area • Shape • Slope • Rock Type • Soil • Land Use • Drainage Density • Precipitation / Temp • Tidal Conditions ©Microsoft Word clipart

Interpretation of Storm Hydrographs Basin lag time You need to refer to: Peak flow Rising li Discharge (m 3/s) 1 0 12 b 4 3 2 im nl mm Overland flow sio 2 s ce • Rising Limb • Recession Limb • Lag time • Rainfall Intensity • Peak flow compared to Base flow • Recovery rate, back to Base flow Re mb 3 Through flow 24 Base flow 36 48 30 Hours from start of rain storm 72

Area Large basins receive more precipitation than small therefore have larger runoff Larger size means longer lag time as water has a longer distance to travel to reach the trunk river Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Shape Elongated basin will produce a lower peak flow and longer lag time than a circular one of the same size Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Slope Channel flow can be faster down a steep slope therefore steeper rising limb and shorter lag time Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Rock Type Permeable rocks mean rapid infiltration and little overland flow therefore shallow rising limb Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Soil Infiltration is generally greater on thick soil, although less porous soils eg. clay act as impermeable layers The more infiltration occurs the longer the lag time and shallower the rising limb Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Land Use Urbanisation - concrete and tarmac form impermeable surfaces, creating a steep rising limb and shortening the time lag Afforestation - intercepts the precipitation, creating a shallow rising limb and lengthening the time lag Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Drainage Density A higher density will allow rapid overland flow Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Precipitation & Temperature Short intense rainstorms can produce rapid overland flow and steep rising limb If there have been extreme temperatures, the ground can be hard (either baked or frozen) causing rapid surface run off Snow on the ground can act as a store producing a long lag time and shallow rising limb. Once a thaw sets in the rising limb will become steep Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Tidal Conditions High spring tides can block the normal exit for the water, therefore extending the length of time the river basin takes to return to base flow Area Shape Slope Rock Type Soil Land Use Drainage Density Precipitation / Temp Tidal Conditions

Hydrograph Analysis 26

Hydrograph Analysis : Hydrograph : Q vs t • • • Duration , t Lag Time , t. L Time of Concentration , tc Rising Limb Recession Limb (falling limb) Peak Flow , Qp Time to Peak (rise time), tp Recession Curve Base flow , BF Separation of BF from Runoff 27

Hydrograph Components Taken from Wanielista, M. , R. Kersten, and R. Eaglin, Hydrology: Water Quantity and Quality Control, p. 184

Graphical Representation Duration of excess precipitation. Lag time Time of concentration Base flow 29

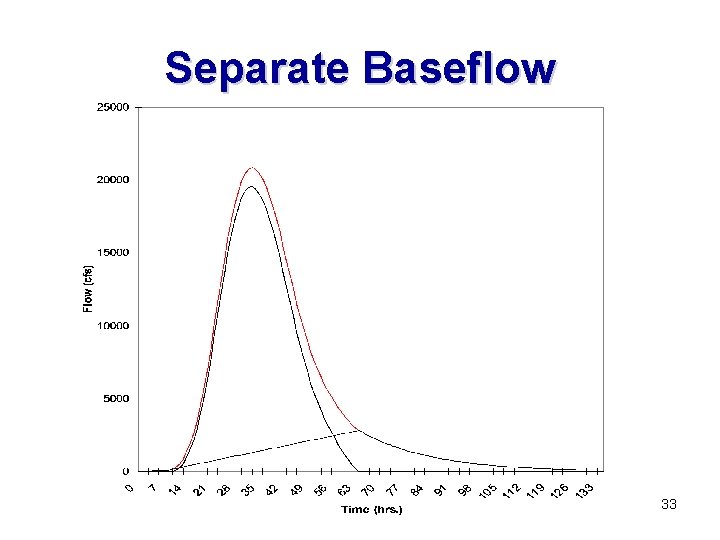
Separation of Baseflow ü. . . generally accepted that the inflection point on the recession limb of a hydrograph is the result of a change in the controlling physical processes of the excess precipitation flowing to the basin outlet. üIn this example, base flow is considered to be a straight line connecting that point at which the hydrograph begins to rise rapidly and the inflection point on the recession side of the hydrograph. üthe inflection point may be found by plotting the hydrograph in semi-log fashion with flow being plotted on the log scale and noting the time at which the recession side fits a straight line. 30

Separation of Baseflow 31

Hydrograph & Baseflow 32

Separate Baseflow 33

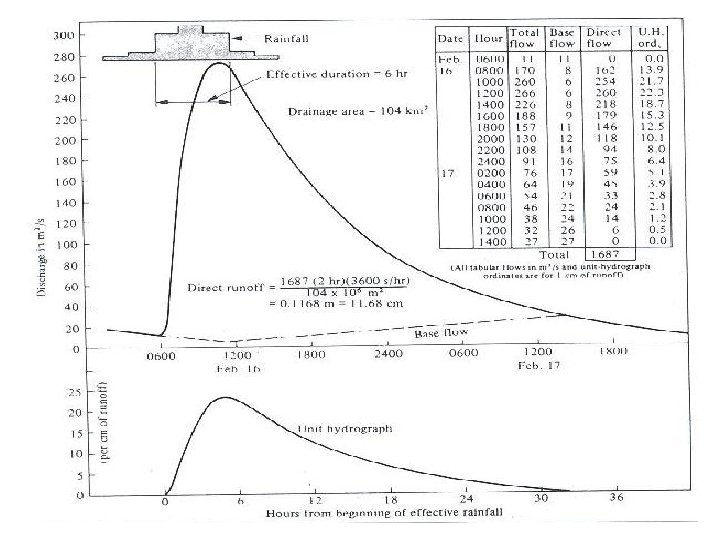
Q = d * UH Runoff = rainfall depth * Unit Hydrograph 34

Unit Hydrograph(UH) Theory: • Sherman - 1932 • Horton - 1933 • Wisler & Brater - 1949 – “the hydrograph of surface runoff resulting from a relatively short, intense rain, called a unit storm. ” • The runoff hydrograph may be “made up” of runoff that is generated as flow through the soil (Black, 1990). 35

Unit Hydrograph • The hydrograph (direct runoff)resulting from 1 inch (or 1 cm) of excess precipitation spread uniformly in space and time over a watershed for a given duration. • The key points : ü 1 -inch (1 cm) of EXCESS precipitation üSpread uniformly over space - evenly over the watershed üUniformly in time - the excess rate is constant over the time interval üThere is a given duration. t-UH (ex. 2 hr-UH) 36

37

Methods of Developing UH’s • From Streamflow Data • Synthetically – Snyder – SCS – Time-Area (Clark, 1945) • “Fitted” Distributions • Geomorphologic 38

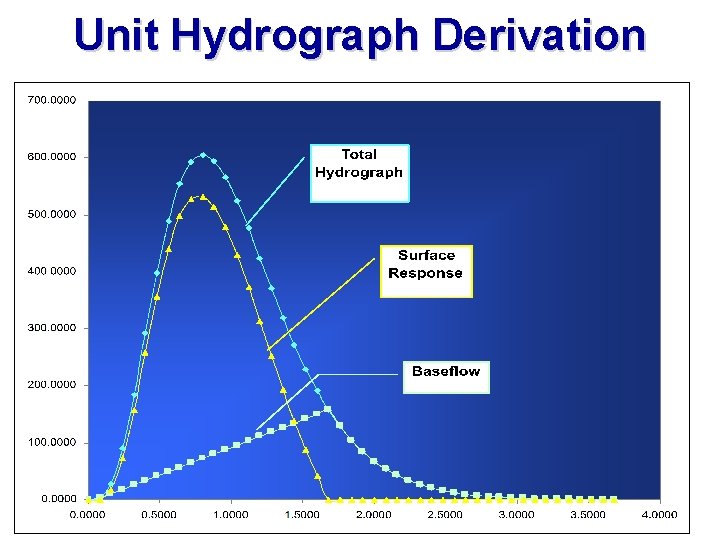
Unit Hydrograph Derivation • i) Tabulate the total hydrograph with time distribution. • ii) Tabulate the baseflow if given or separate with method of our choice. • iii) Find the Direct Runoff Hydrograph(DRH) by subtracting the baseflow from the total hydrograph. ( DRH = Q – BF ) • iv) Find the volume of water under the DRH • Vol. = Σ Q * Δt

Unit Hydrograph Derivation 40

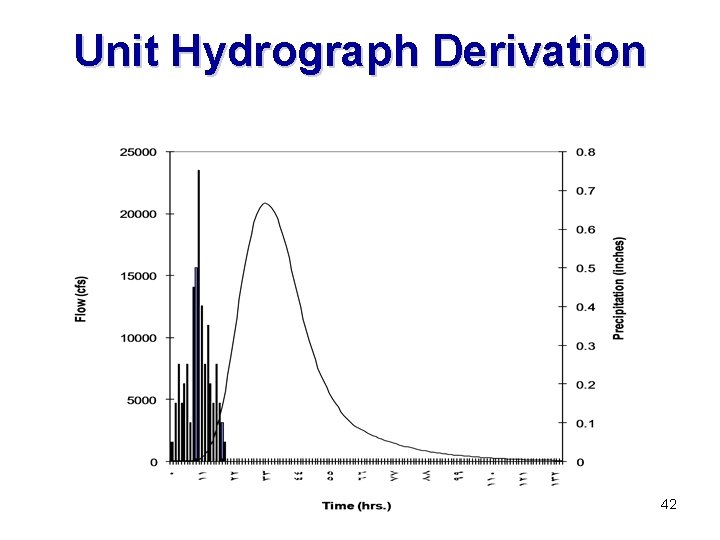
Unit Hydrograph Derivation • v) Divide the volume of water(step iv) by the drainage area(A) to get effective rainfall(de) (runoff) per unit area. de = vol. / A • vi) Divide the ordinates of the DRH by the de of effective rainfall(step v). • The result is a unit hydrograph(UH) for the duration of storm.

Unit Hydrograph Derivation 42

43

Obtain UH Ordinates • The ordinates of the unit hydrograph are obtained by dividing each flow in the direct runoff hydrograph by the depth of excess precipitation. • In this example, the units of the unit hydrograph would be cfs/inch (of excess precipitation). 45

Final UH 46

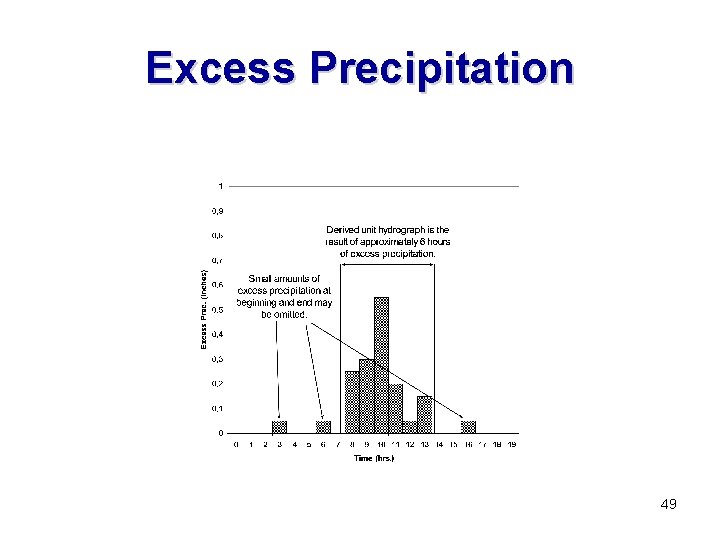
Determine Duration of UH • The duration of the derived unit hydrograph is found by examining the precipitation for the event and determining that precipitation which is in excess. • This is generally accomplished by plotting the precipitation in hyetograph form and drawing a horizontal line such that the precipitation above this line is equal to the depth of excess precipitation as previously determined. • This horizontal line is generally referred to as the F-index and is based on the assumption of a constant or uniform infiltration rate. • The uniform infiltration necessary to cause 1. 65 inches of excess precipitation was determined to be approximately 0. 2 inches per hour. 47

Estimating Excess Precip. 0. 8 0. 7 Precipitation (inches) 0. 6 0. 5 Uniform loss rate of 0. 2 inches per hour. 0. 4 0. 3 0. 2 0. 1 0 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Time (hrs. ) 48

Excess Precipitation 49

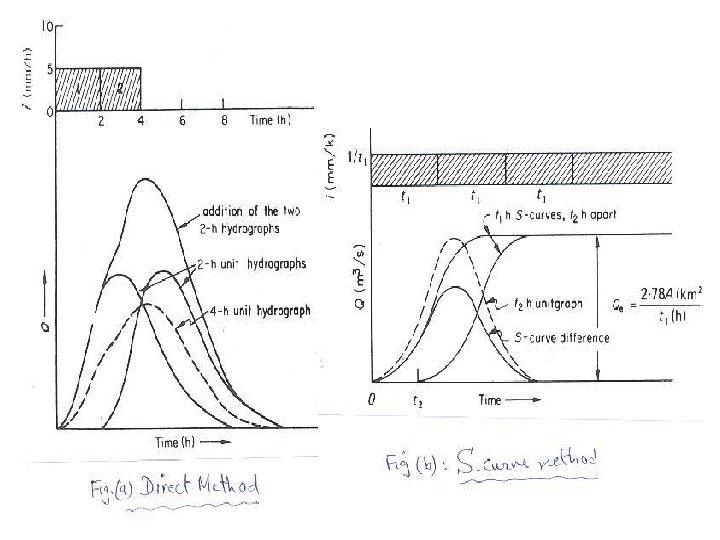
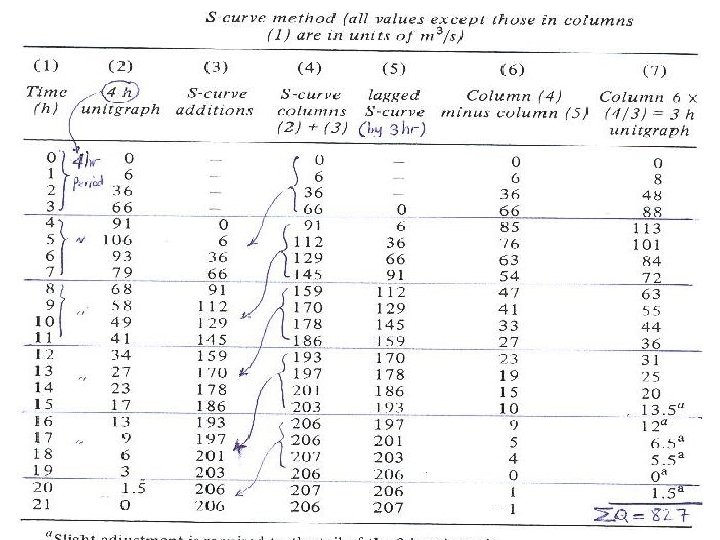
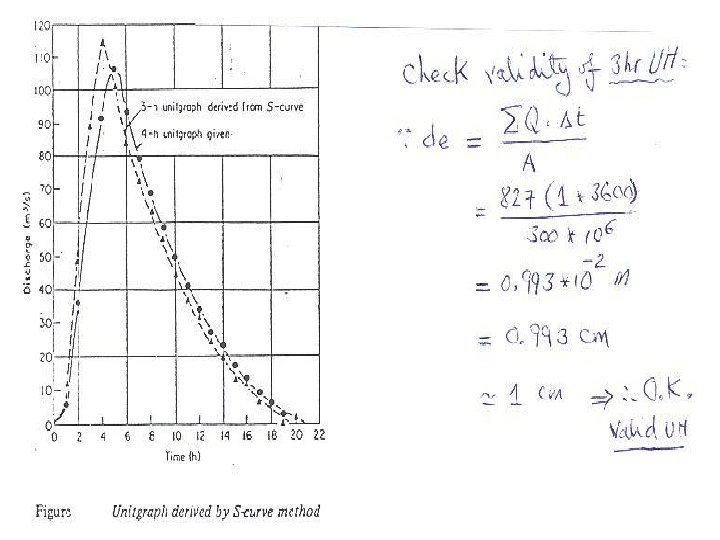
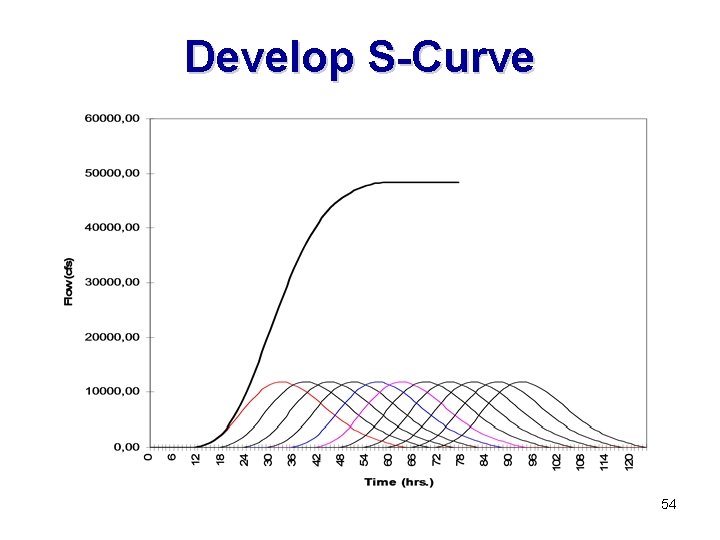
Changing the Duration • Very often, it will be necessary to change the duration of the unit hydrograph. • If unit hydrographs are to be averaged, then they must be of the same duration. • Also, convolution of the unit hydrograph with a precipitation event requires that the duration of the unit hydrograph be equal to the time step of the incremental precipitation. • The most common method of altering the duration of a unit hydrograph is by the S-curve method. • The S-curve method involves continually lagging a unit hydrograph by its duration and adding the ordinates. • For the present example, the 6 -hour unit hydrograph is continually lagged by 6 hours and the ordinates are added. 50

51

52

53

Develop S-Curve 54

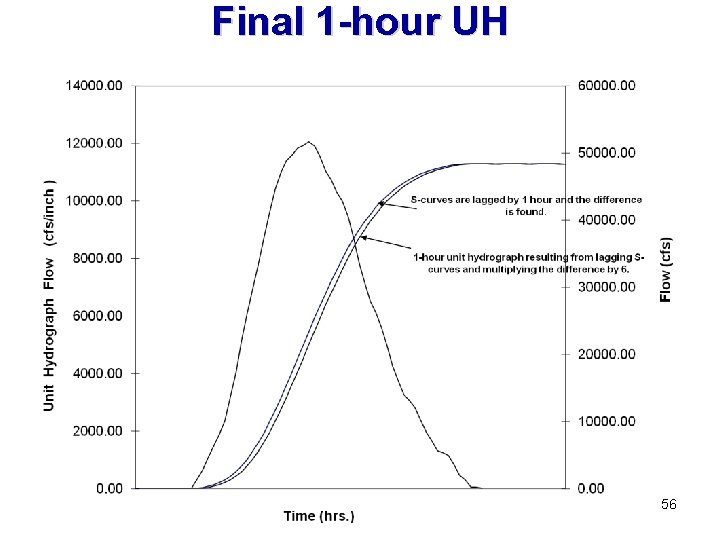
Convert to 1 -Hour Duration • To arrive at a 1 -hour unit hydrograph, the S-curve is lagged by 1 hour and the difference between the two lagged S-curves is found to be a 1 hour unit hydrograph. • However, because the S-curve was formulated from unit hydrographs having a 6 hour duration of uniformly distributed precipitation, the hydrograph resulting from the subtracting the two S-curves will be the result of 1/6 of an inch of precipitation. • Thus the ordinates of the newly created 1 -hour unit hydrograph must be multiplied by 6 in order to be a true unit hydrograph. • The 1 -hour unit hydrograph should have a higher peak which occurs earlier than the 6 -hour unit hydrograph. 55

Final 1 -hour UH 56

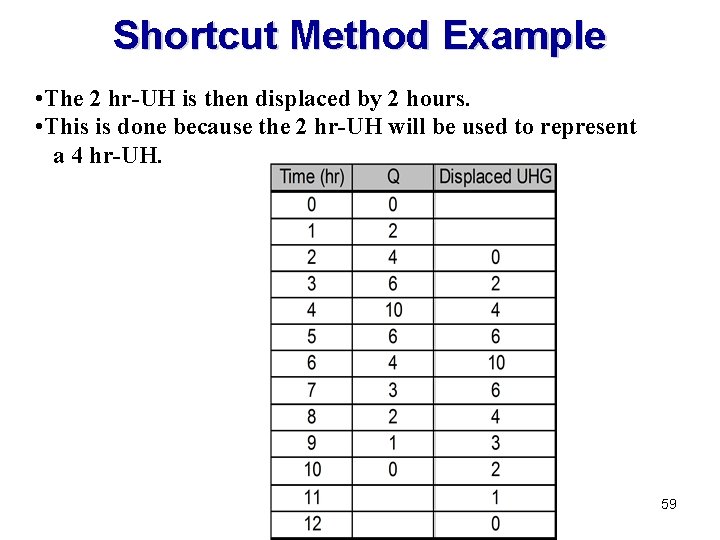
Shortcut Method • There does exist a shortcut method for changing the duration of the unit hydrograph if the two durations are multiples of one another. • This is done by displacing the unit hydrograph. • For example, if you had a two hour unit hydrograph and you wanted to change it to a four hour unit hydrograph. 57

Shortcut Method Example • First, a two hour unit hydrograph is given and a four hour unit hydrograph is needed. • There are two possibilities, develop the S - curve or since they are multiples use the shortcut method. 58

Shortcut Method Example • The 2 hr-UH is then displaced by 2 hours. • This is done because the 2 hr-UH will be used to represent a 4 hr-UH. 59

Shortcut Method Example • These two hydrographs are then summed. 60

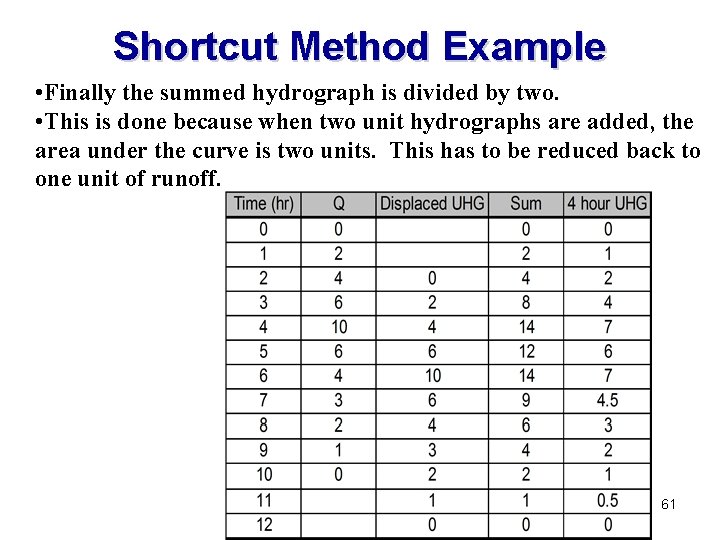
Shortcut Method Example • Finally the summed hydrograph is divided by two. • This is done because when two unit hydrographs are added, the area under the curve is two units. This has to be reduced back to one unit of runoff. 61

Average Several UH’s • It is recommend that several unit hydrographs be derived and averaged. • The unit hydrographs must be of the same duration in order to be properly averaged. • It is often not sufficient to simply average the ordinates of the unit hydrographs in order to obtain the final unit hydrograph. A numerical average of several unit hydrographs which are different “shapes” may result in an “unrepresentative” unit hydrograph. • It is often recommended to plot the unit hydrographs that are to be averaged. Then an average or representative unit hydrograph should be sketched or fitted to the plotted unit hydrographs. • Finally, the average unit hydrograph must have a volume of 1 inch of runoff for the basin. 62

Synthetic UHG’s • • Snyder SCS Time-area IHABBS Implementation Plan : NOHRSC Homepage http: //www. nohrsc. nws. gov/98/html/uhg/index. html 63

Snyder • Since peak flow and time of peak flow are two of the most important parameters characterizing a unit hydrograph, the Snyder method employs factors defining these parameters, which are then used in the synthesis of the unit graph (Snyder, 1938). • The parameters are Cp, the peak flow factor, and Ct, the lag factor. • The basic assumption in this method is that basins which have similar physiographic characteristics are located in the same area will have similar values of Ct and Cp. • Therefore, for ungaged basins, it is preferred that the basin be near or similar to gaged basins for which 64 these coefficients can be determined.

Basic Relationships 65

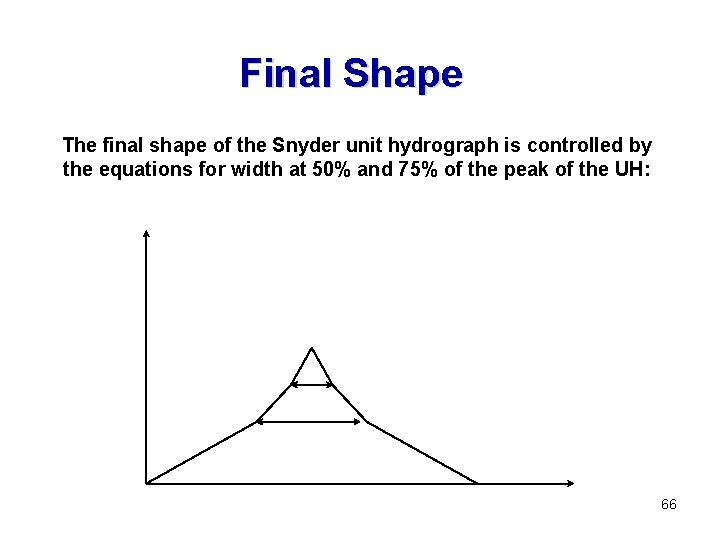
Final Shape The final shape of the Snyder unit hydrograph is controlled by the equations for width at 50% and 75% of the peak of the UH: 66

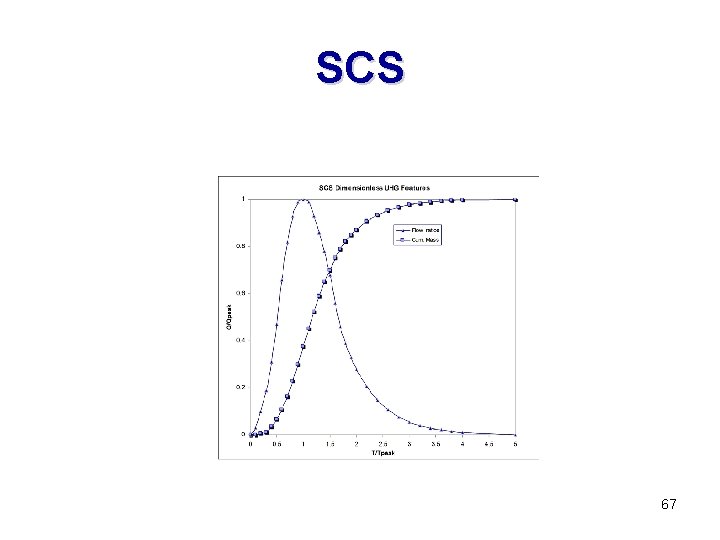
SCS 67

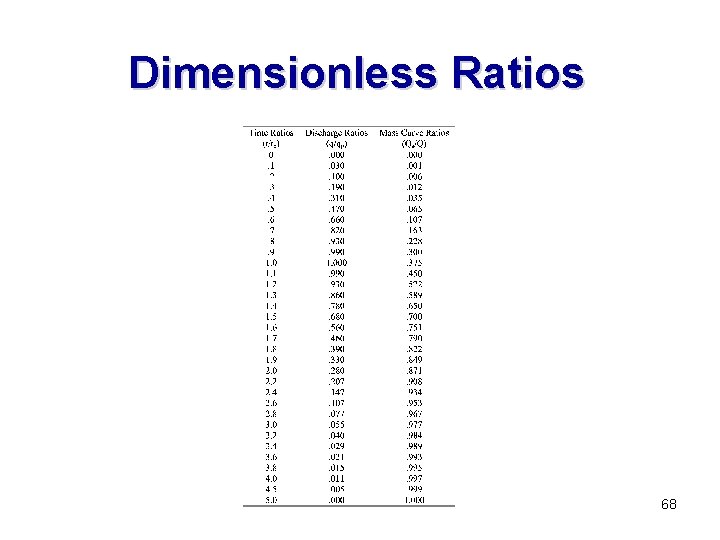
Dimensionless Ratios 68

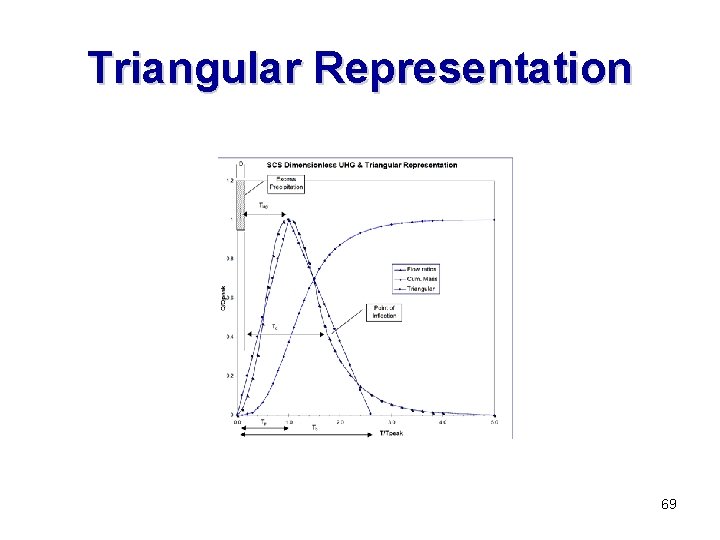
Triangular Representation 69

Triangular Representation The 645. 33 is the conversion used for delivering 1 -inch of runoff (the area under the unit hydrograph) from 1 -square mile in 1 -hour (3600 seconds). 70

484 ? Comes from the initial assumption that 3/8 of the volume under the UHG is under the rising limb and the remaining 5/8 is under the recession limb. 71

Duration & Timing? Again from the triangle L = Lag time For estimation purposes : 72

Time of Concentration • Regression Eqs. • Segmental Approach 73

A Regression Equation where : Tlag = lag time in hours L = Length of the longest drainage path in feet S = (1000/CN) - 10 (CN=curve number) %Slope = The average watershed slope in % 74

Segmental Approach • More “hydraulic” in nature • The parameter being estimated is essentially the time of concentration or longest travel time within the basin. • In general, the longest travel time corresponds to the longest drainage path • The flow path is broken into segments with the flow in each segment being represented by some type of flow regime. • The most common flow representations are overland, sheet, rill and gully, and channel flow. 75

A Basic Approach Mc. Cuen (1989) and SCS (1972) provide values of k for several flow situations (slope in %) Sorell & Hamilton, 1991 76

Triangular Shape • In general, it can be said that the triangular version will not cause or introduce noticeable differences in the simulation of a storm event, particularly when one is concerned with the peak flow. • For long term simulations, the triangular unit hydrograph does have a potential impact, due to the shape of the recession limb. • The U. S. Army Corps of Engineers (HEC 1990) fits a Clark unit hydrograph to match the peak flows estimated by the Snyder unit hydrograph procedure. • It is also possible to fit a synthetic or mathematical function to the peak flow and timing parameters of the desired unit hydrograph. • Aron and White (1982) fitted a gamma probability distribution using peak flow and time to peak data. 77

Fitting a Gamma Distribution 78

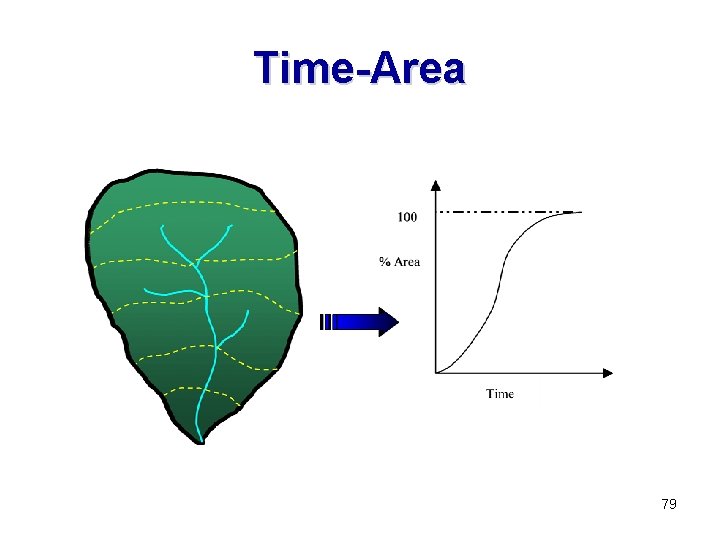
Time-Area 79

Time-Area 80

Time-Area 81

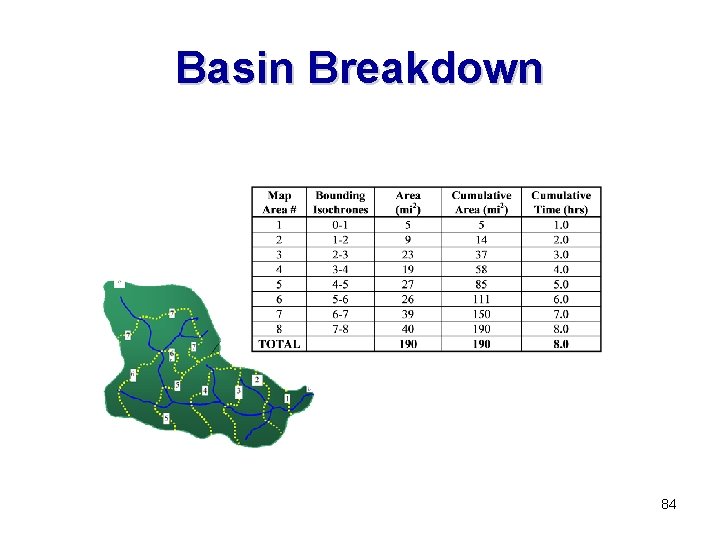
Hypothetical Example • A 190 mi 2 watershed is divided into 8 isochrones of travel time. • The linear reservoir routing coefficient, R, estimated as 5. 5 hours. • A time interval of 2. 0 hours will be used for the computations. 82

Rule of Thumb R - The linear reservoir routing coefficient can be estimated as approximately 0. 75 times the time of concentration. 83

Basin Breakdown 84

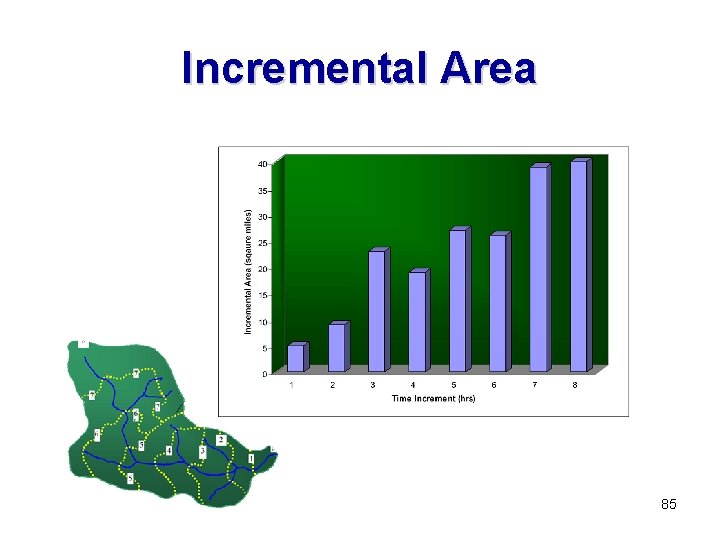
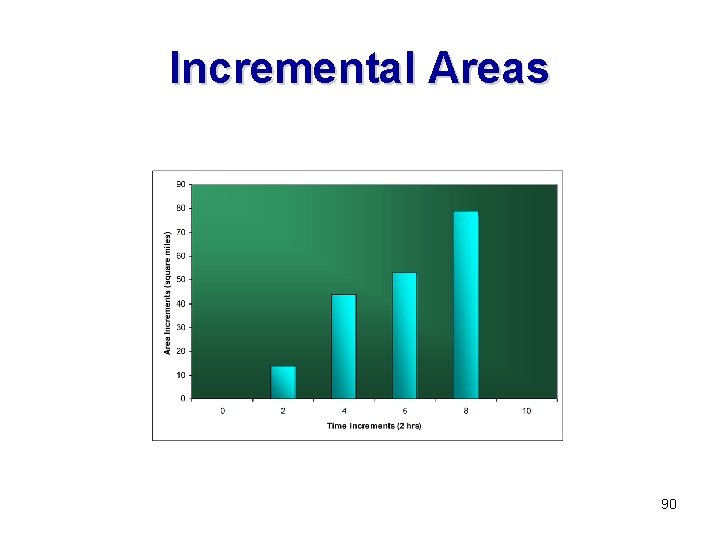
Incremental Area 85

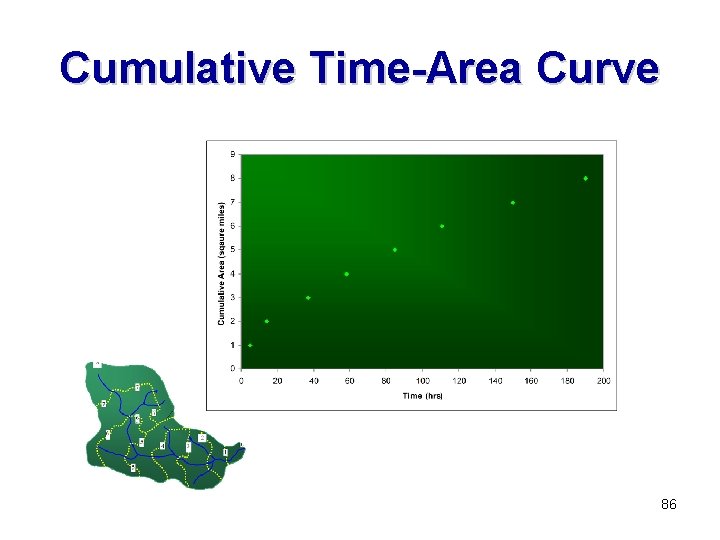
Cumulative Time-Area Curve 86

Trouble Getting a Time-Area Curve? Synthetic time-area curve The U. S. Army Corps of Engineers (HEC 1990) 87

Instantaneous UHG ü Dt = the time step used n the calculation of the translation unit hydrograph ü The final unit hydrograph may be found by averaging 2 instantaneous unit hydrographs that are a Dt time step apart. 88

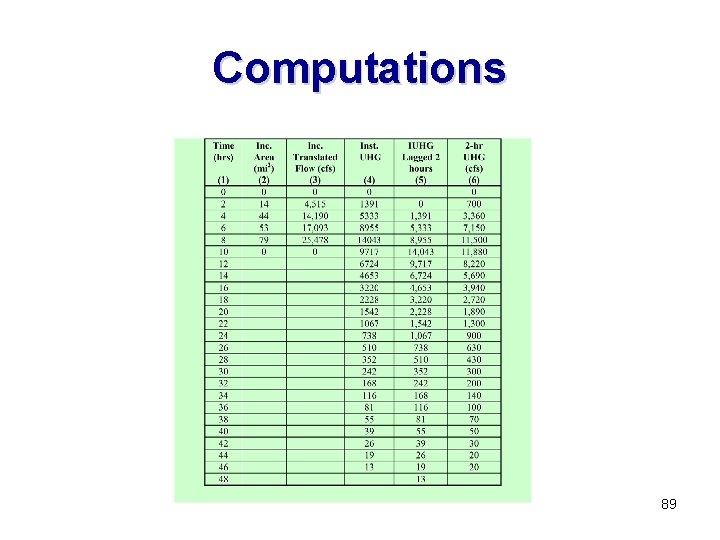
Computations 89

Incremental Areas 90

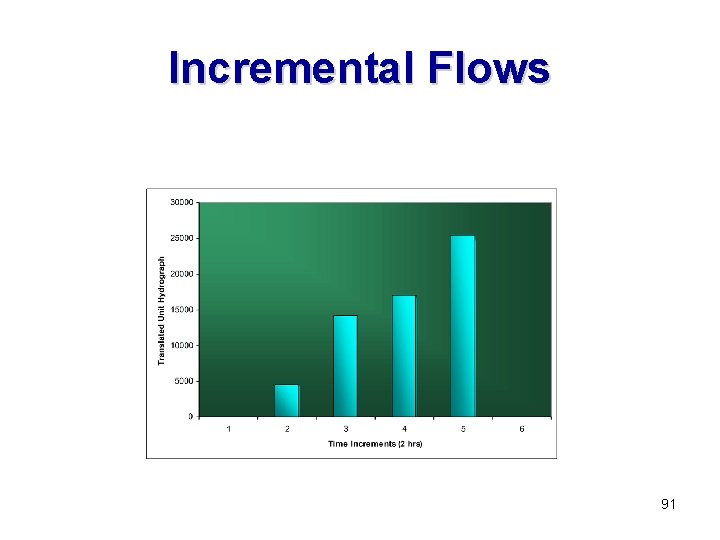
Incremental Flows 91

Instantaneous UHG 92

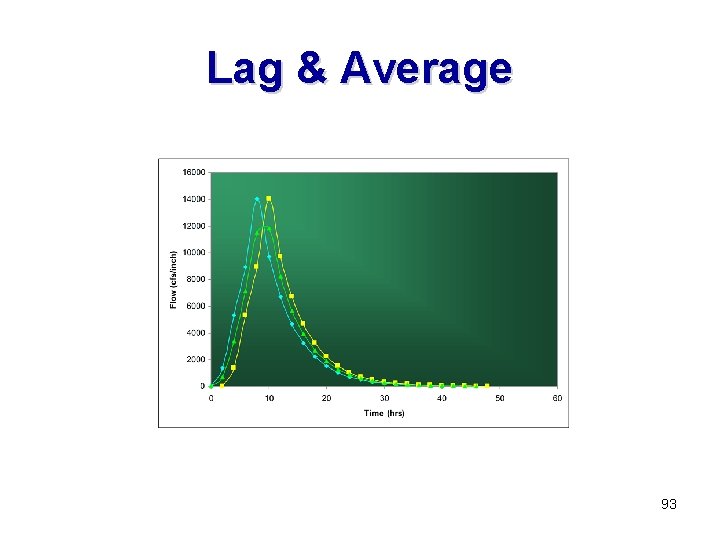
Lag & Average 93

Geomorphologic • Uses stream network topology and probability concepts • Law of Stream Numbers range: 3 -5 • Law of Stream Lengths range: 1. 5 -3. 5 • Law of Stream Areas range: 3 -6 94

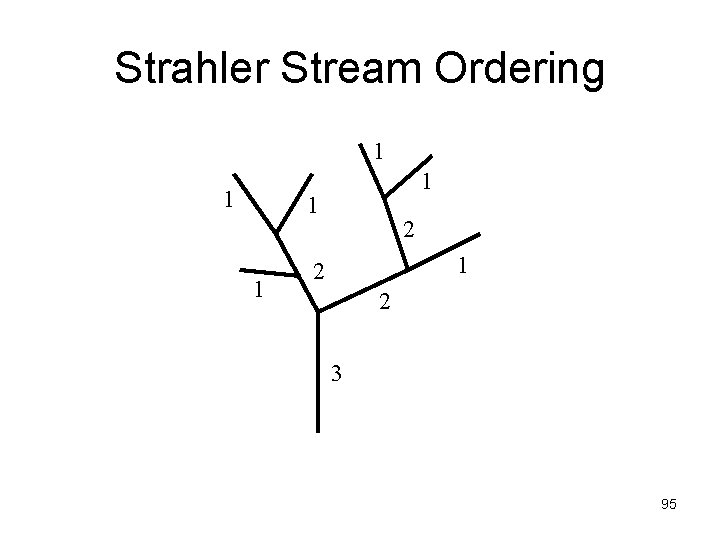
Strahler Stream Ordering 1 1 1 2 2 3 95

Probability Concepts • Water travels through basin, making transitions from lower to higher stream order • Travel times and transition probabilities can be approximated using Strahler stream ordering scheme • Obtain a probability density function analogous to an instantaneous unit hydrograph • Can ignore surface/subsurface travel times to get a channelbased GIUH 96

GIUH Equations • Channel-based, triangular instantaneous unit hydrograph: • LW in km, V in m/s, qp in hr-1, tp in hrs 97