CE 40763 Digital Signal Processing AD Sampling Upsampling

CE 40763 Digital Signal Processing A/D, Sampling, Upsampling, and Downsampling Hossein Sameti Department of Computer Engineering Sharif University of Technology

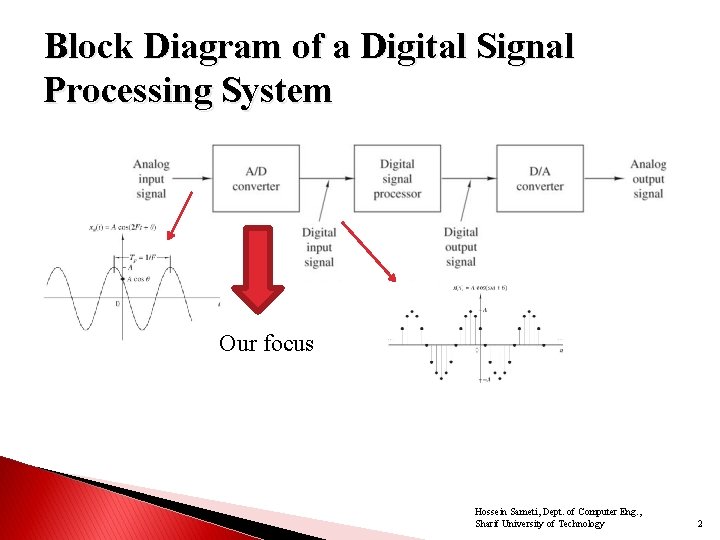
Block Diagram of a Digital Signal Processing System Our focus Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 2

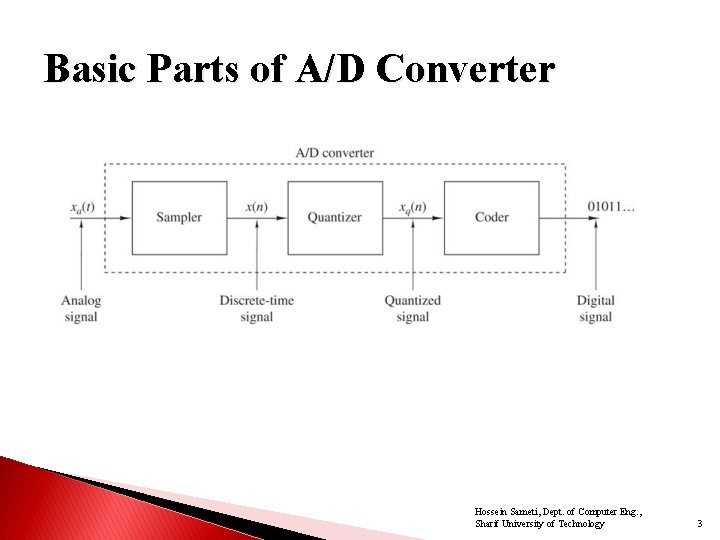
Basic Parts of A/D Converter Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 3

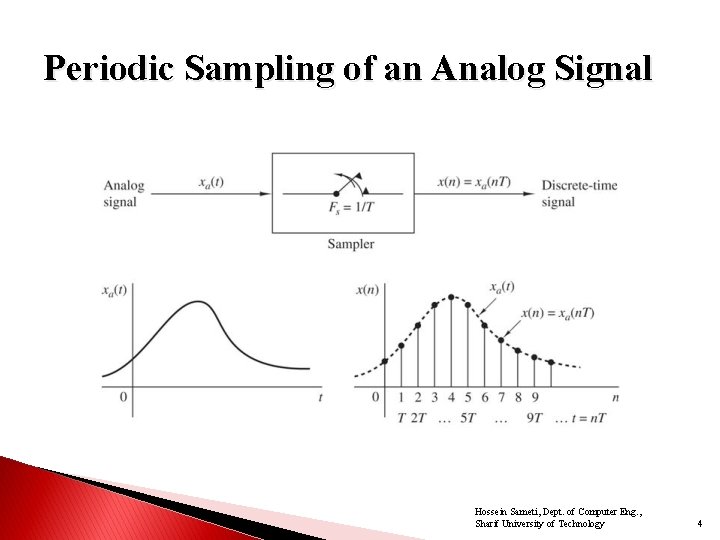
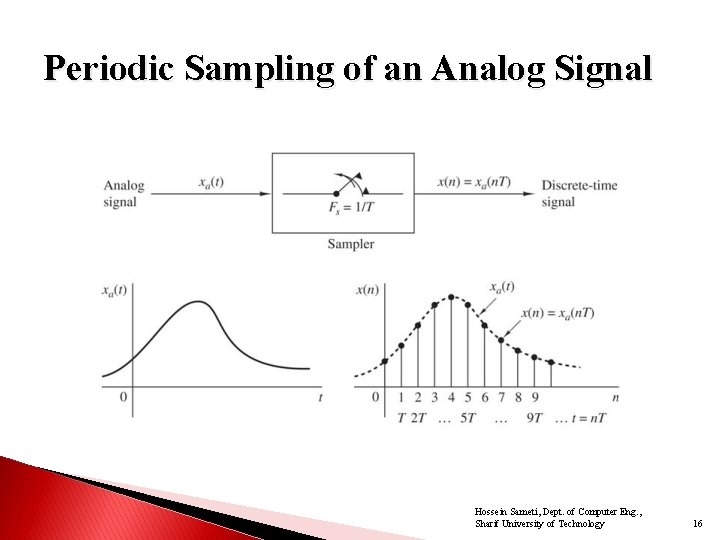
Periodic Sampling of an Analog Signal Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 4

Periodic Sampling (cont’d) In practice, the sampling is performed by a S/H circuit. Sample-and-hold (S/H) S/H is an analog circuit that tracks the analog signal during the sample mode and holds it during the hold mode. The time needed for conversion should be less than the hold mode duration. The sampling period T should be greater than the duration of sample & hold mode Copyright: NEC 5

Sample-and-hold (S/H) The goal of the S/H is to continuously sample the input and then hold the value constant as long as it takes the A/D converter to digitally represent (code) the samples. Thus, it allows the A/D converter to operate more slowly than the time needed to acquire a sample. S/H is of critical importance in digital conversion of signals that change rapidly (i. e. the signals with large bandwidth). Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 6

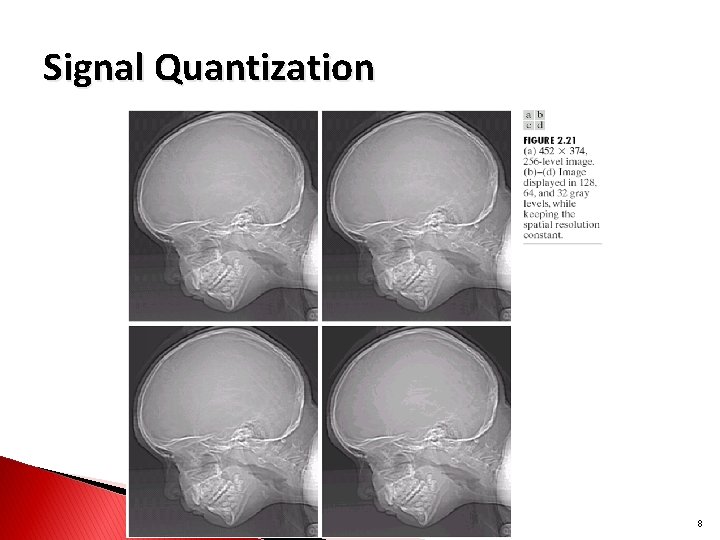
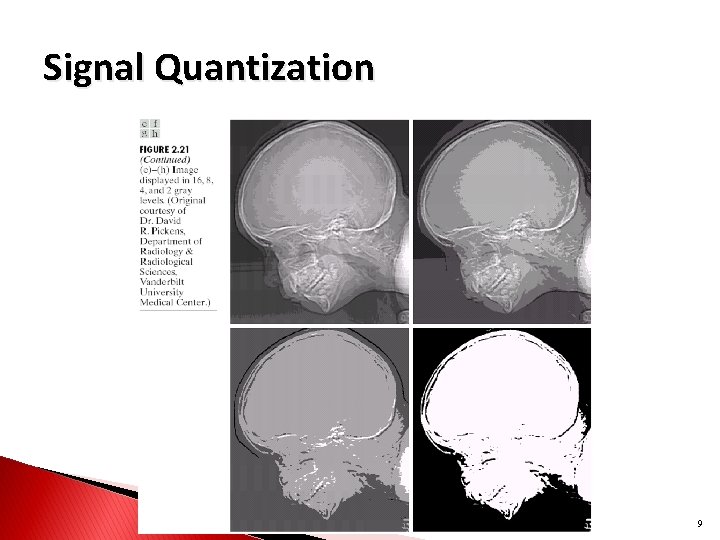
Signal Quantization Quantization: conversion of continuous-valued signal into discrete -valued. Quantization effects: reducing quantized levels results in signal quality degradation. Quantization is irreversible: results in loss of information. Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 7

Signal Quantization 8

Signal Quantization 9

One solution for Signal Quantization: Flash Converter Uses a reference and a comparator for each of the discrete levels represented in the digital output Number of comparators = number of quantization levels generally fast but expensive 10

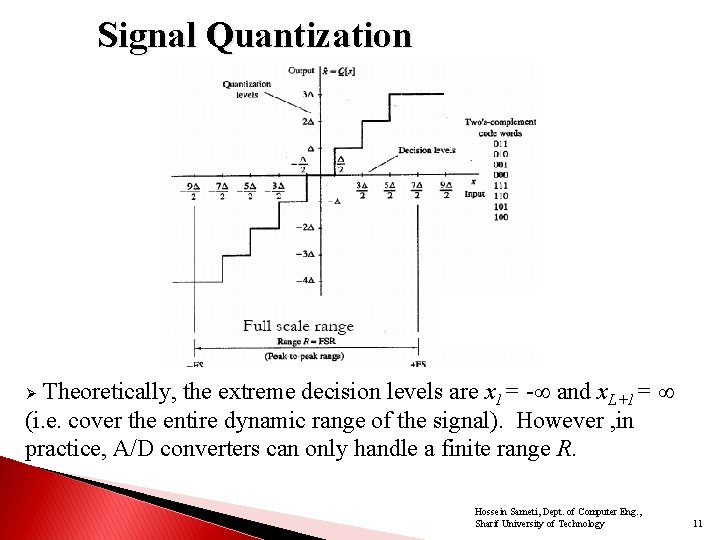
Signal Quantization Theoretically, the extreme decision levels are x 1= - and x. L+1= (i. e. cover the entire dynamic range of the signal). However , in practice, A/D converters can only handle a finite range R. Ø Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 11

Coding During coding, A/D converters assign a unique binary representation to each quantization level. Ø Ø If we have L quantization levels, then we need to have where B is the number of bits needed for the binary representation. Ø Quantization error: Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 12

Analysis of Quantization Errors Each sample of the signal is quantized to one of the amplitude levels, where B is the number of bits used to represent each sample. The quantized waveform is modeled as : e(n) represent the quantization error, Which we treat as an additive noise. Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 13

Analysis of Quantization Errors ◦ For small , it is reasonable to assume that random variable uniformly distributed from is a to . Where the step size of the quantizer is Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 14

Analysis of Quantization Errors ◦ If is the maximum amplitude of signal, ◦ The mean square value of the quantization error is : ◦ Measured in d. B, The mean square value of the noise is : Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 15

Periodic Sampling of an Analog Signal Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 16

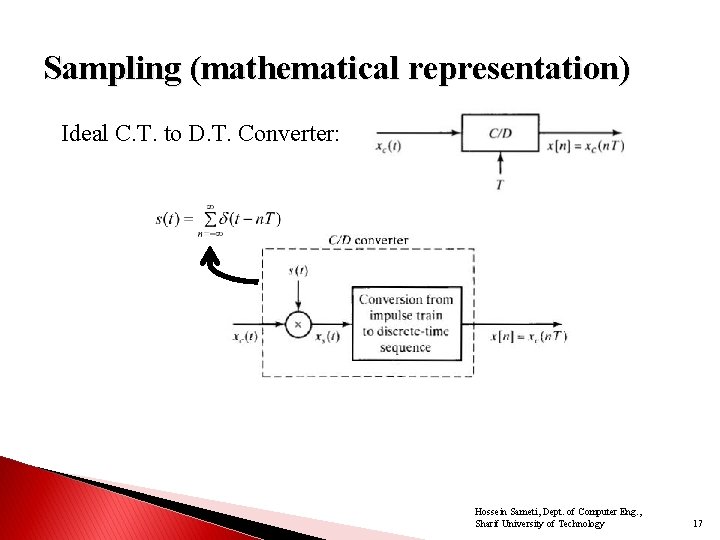
Sampling (mathematical representation) Ideal C. T. to D. T. Converter: Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 17

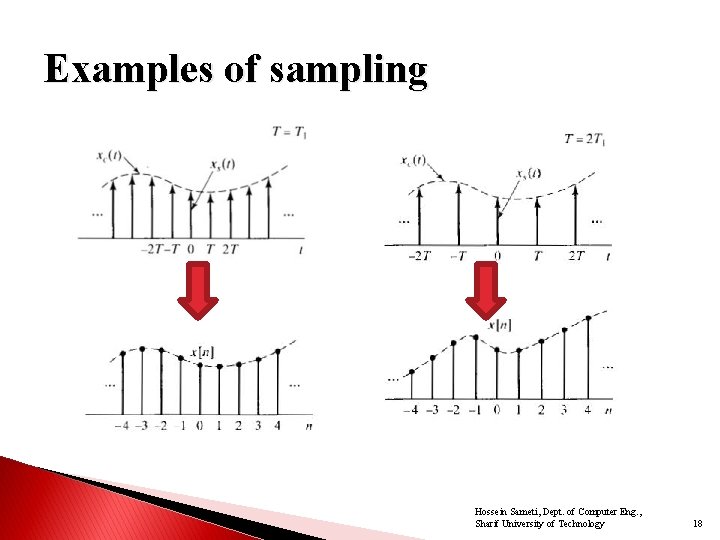
Examples of sampling Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 18

Relationship between CTFT and DTFT Shifting property Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 19

Relationship between CTFT and DTFT CTFT (1) (2) (1), (2) (eq. 3) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 20

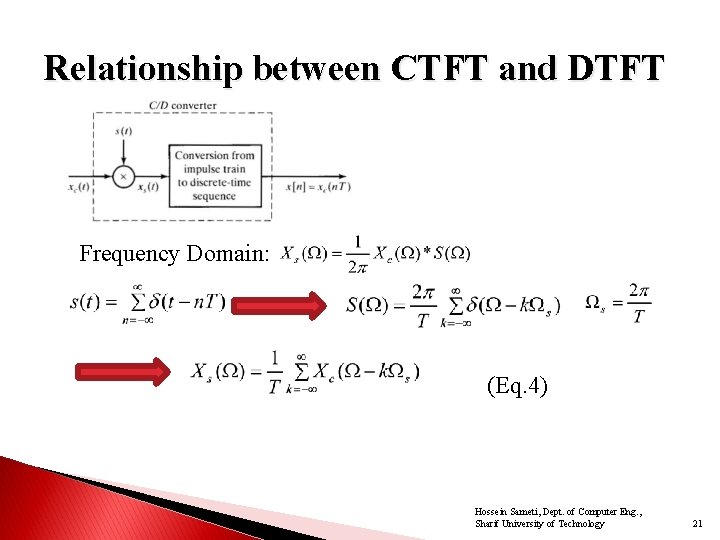
Relationship between CTFT and DTFT Frequency Domain: (Eq. 4) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 21

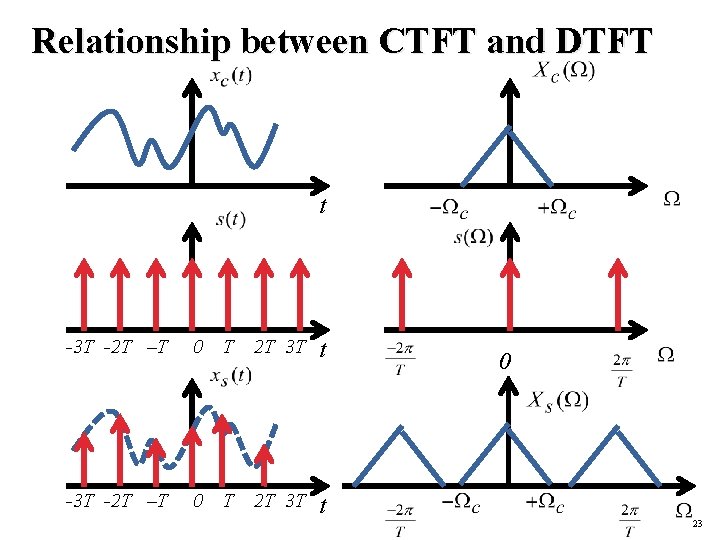
Relationship between CTFT and DTFT (eq. 3) (eq. 4) (eq. 3) and (eq. 4) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 22

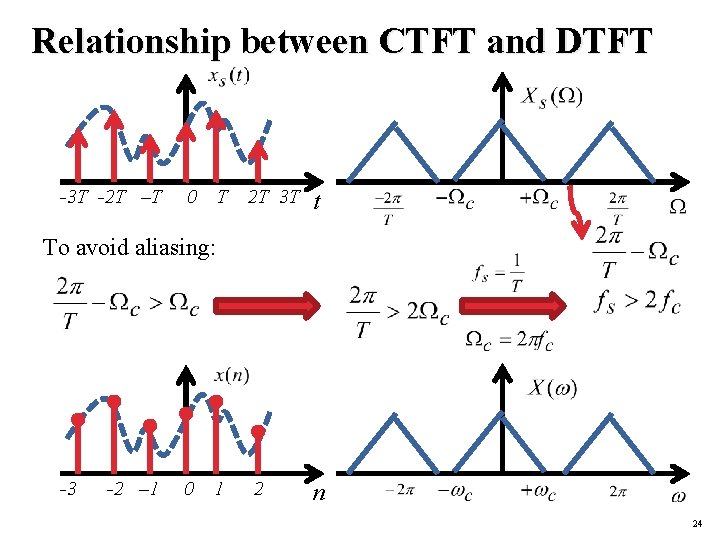
Relationship between CTFT and DTFT t -3 T -2 T –T 0 T 2 T 3 T t 0 23

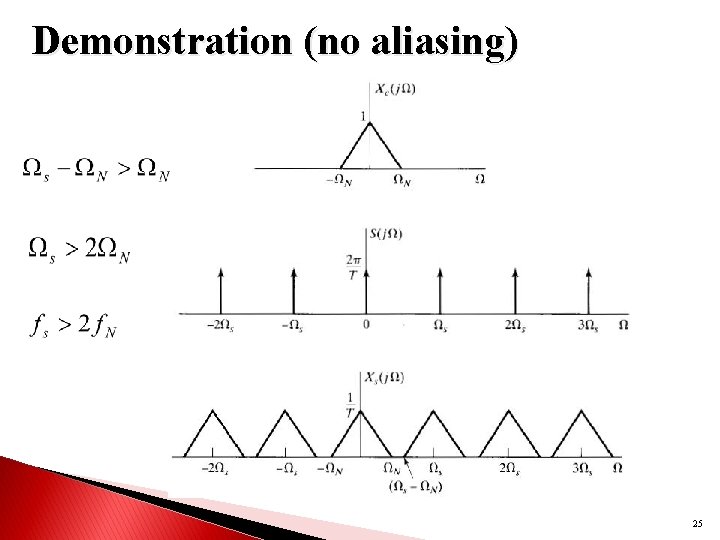
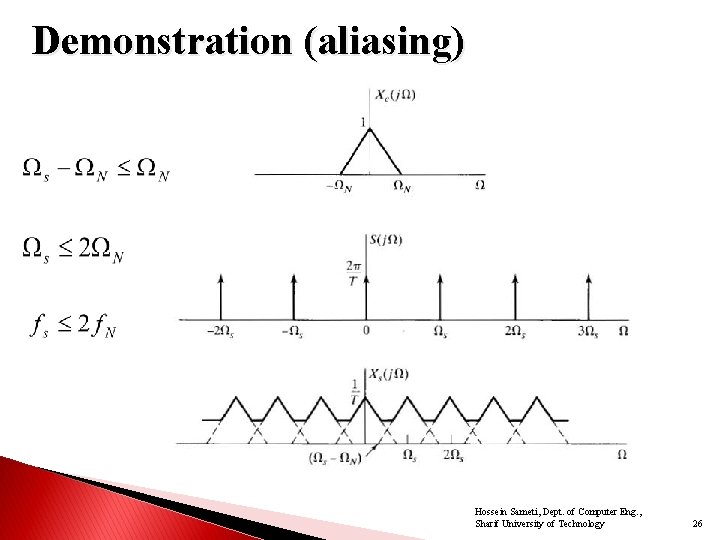
Relationship between CTFT and DTFT -3 T -2 T –T 0 T 2 T 3 T t 1 2 n To avoid aliasing: -3 -2 – 1 0 24

Demonstration (no aliasing) 25

Demonstration (aliasing) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 26

Anti-aliasing Filter General configuration of digital processing systems Anti-aliasing (i. e. pre-) filters are analog filters serving two purposes: ◦ That the bandwidth of the signal to be sampled is limited to the desired frequency range (thus no aliasing). ◦ Limiting the additive noise spectrum and other interference corrupting the desired signal. Thus, it rejects the out-of-band noise. Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 27

Changing the Sampling Rate 28

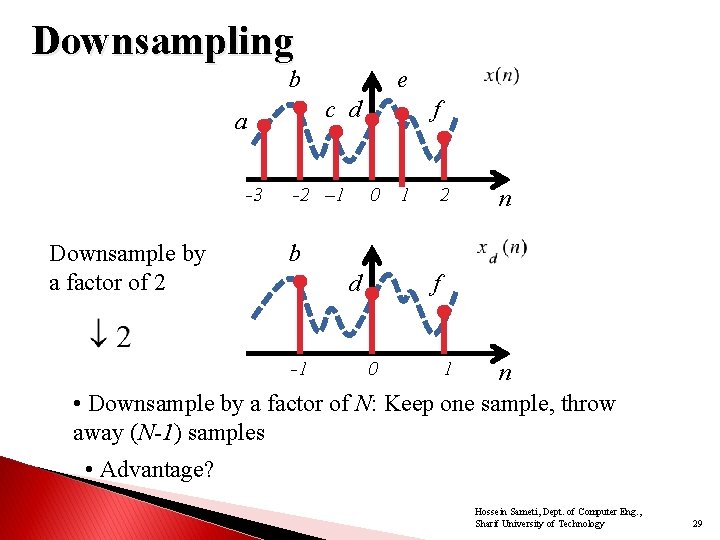
Downsampling b c d a -3 Downsample by a factor of 2 e -2 – 1 f 0 1 2 n b d -1 f 0 1 n • Downsample by a factor of N: Keep one sample, throw away (N-1) samples • Advantage? Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 29

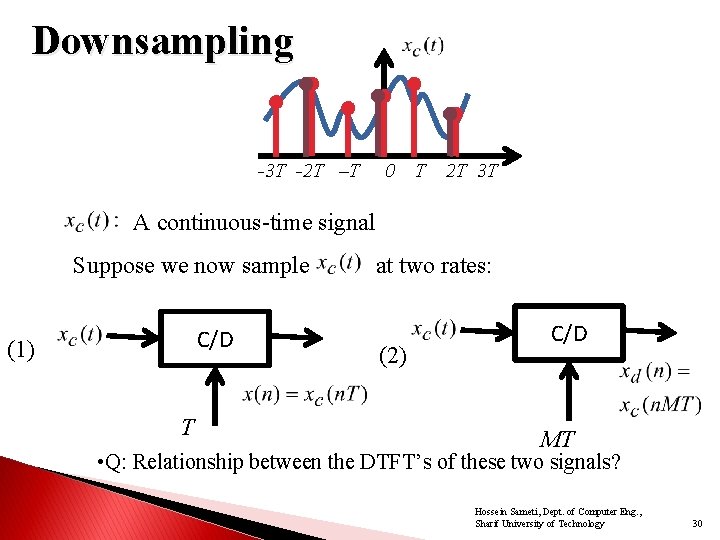
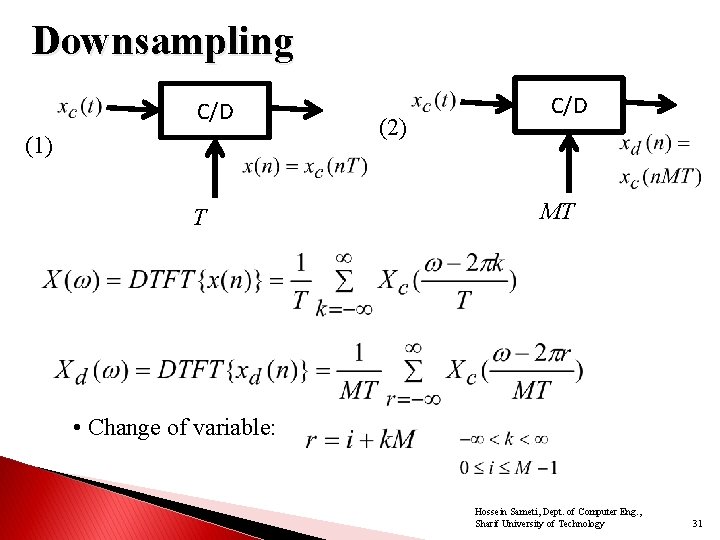
Downsampling -3 T -2 T –T 0 T 2 T 3 T A continuous-time signal Suppose we now sample C/D (1) T at two rates: (2) C/D MT • Q: Relationship between the DTFT’s of these two signals? Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 30

Downsampling C/D (1) T (2) C/D MT • Change of variable: Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 31

Downsampling • Change of variable: Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 32

Downsampling • Change of variable: 33

Downsampling If M=2, 34

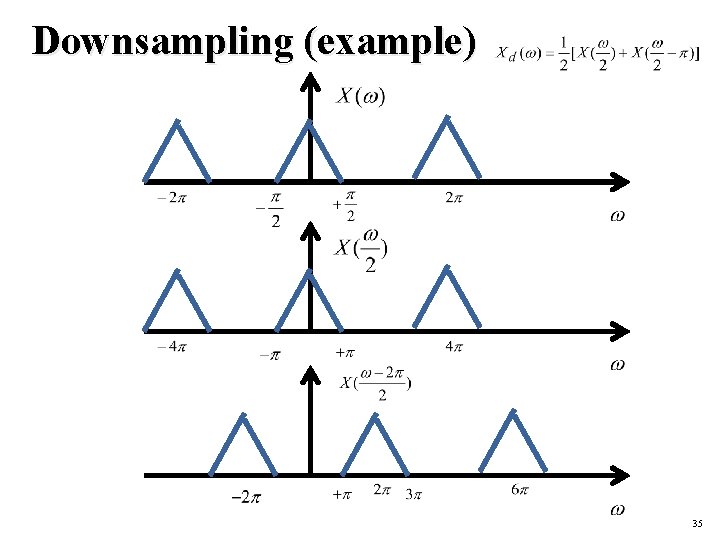
Downsampling (example) 35

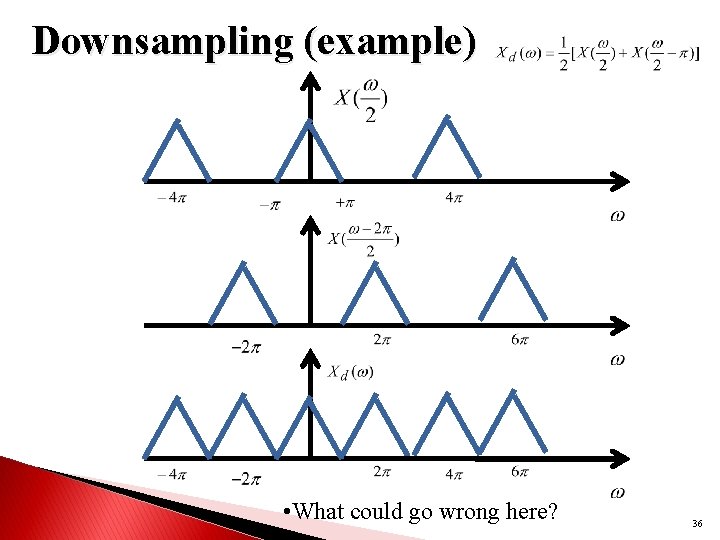
Downsampling (example) • What could go wrong here? 36

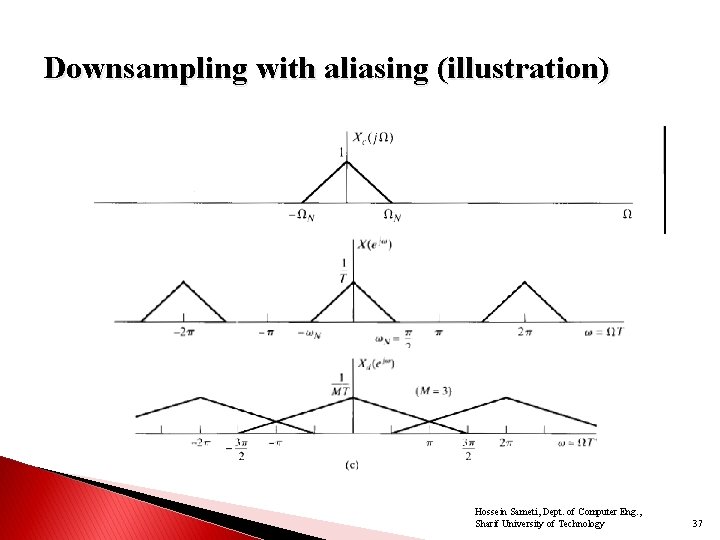
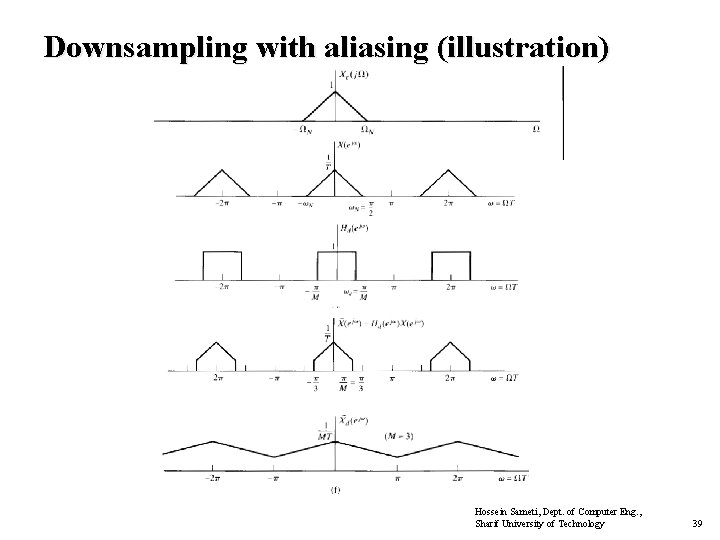
Downsampling with aliasing (illustration) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 37

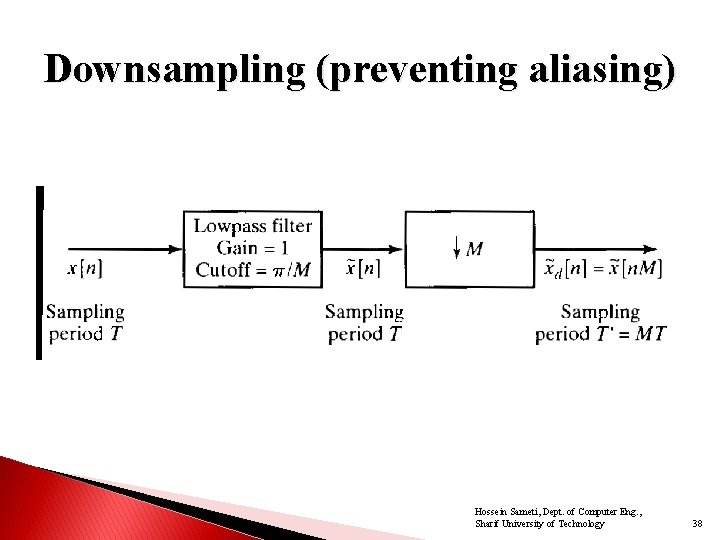
Downsampling (preventing aliasing) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 38

Downsampling with aliasing (illustration) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 39

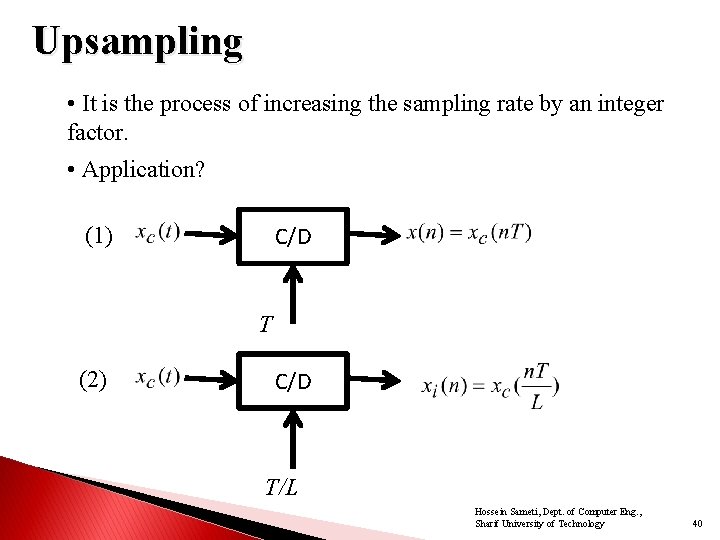
Upsampling • It is the process of increasing the sampling rate by an integer factor. • Application? (1) C/D T (2) C/D T/L Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 40

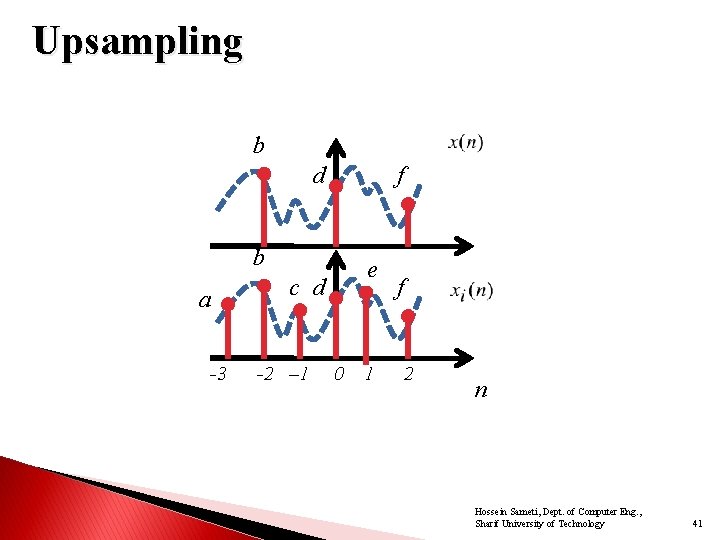
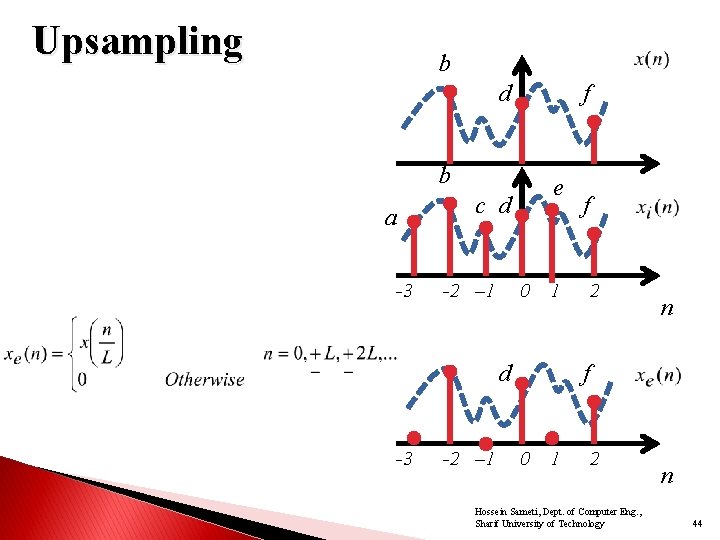
Upsampling b d f b a -3 e c d -2 – 1 0 1 f 2 n Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 41

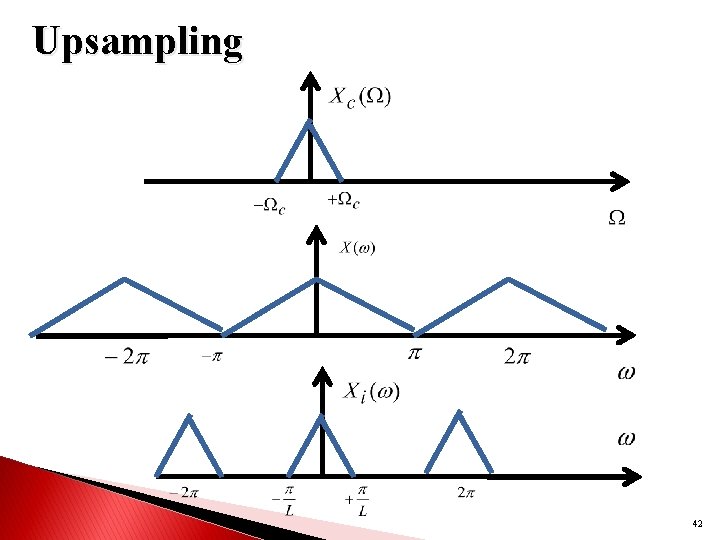
Upsampling 42

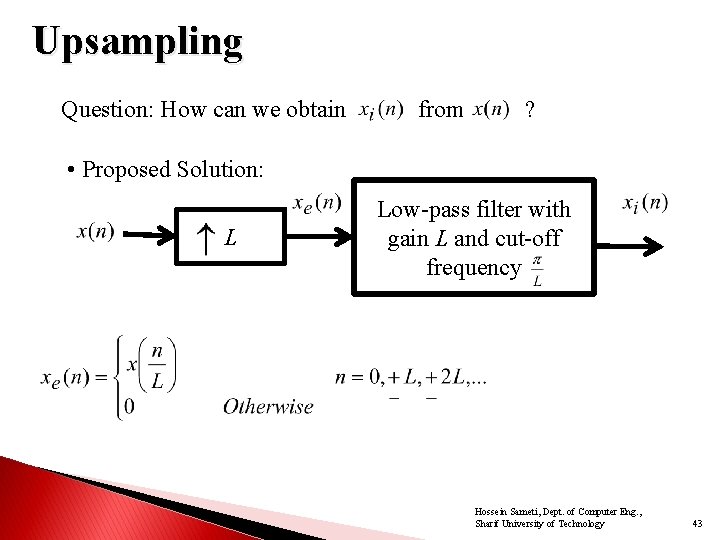
Upsampling Question: How can we obtain from ? • Proposed Solution: L Low-pass filter with gain L and cut-off frequency Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 43

Upsampling b d f b a -3 e c d -2 – 1 0 1 d -3 -2 – 1 f 2 n f 0 1 2 Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology n 44

Upsampling • Q: Relationship between the DTFT’s of these three signals? Shifting property: 45

Upsampling (Eq. 1) On the other hand: (Eq. 2) (Eq. 1) and (Eq. 2) Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 46

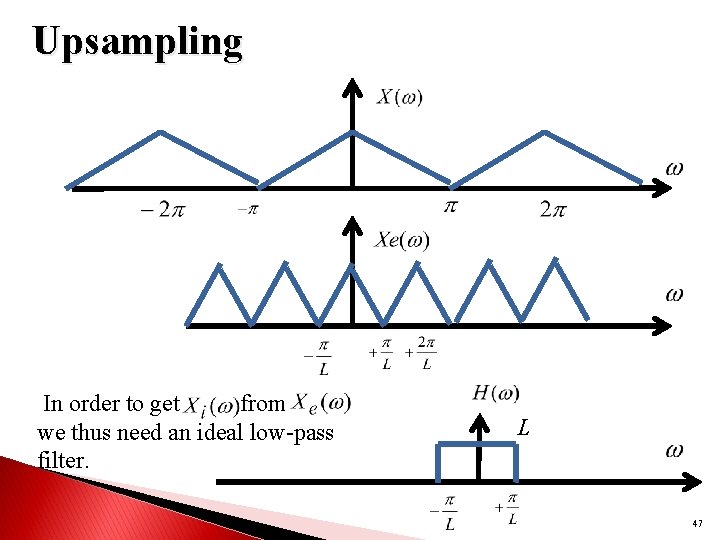
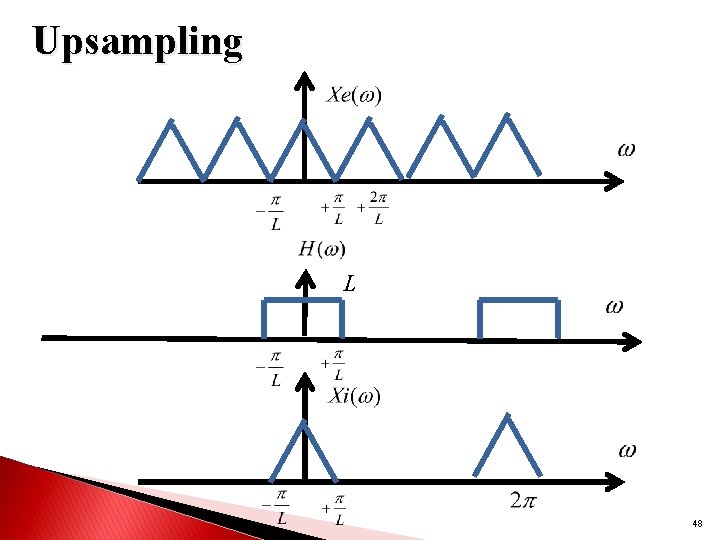
Upsampling In order to get from we thus need an ideal low-pass filter. L 47

Upsampling L 48

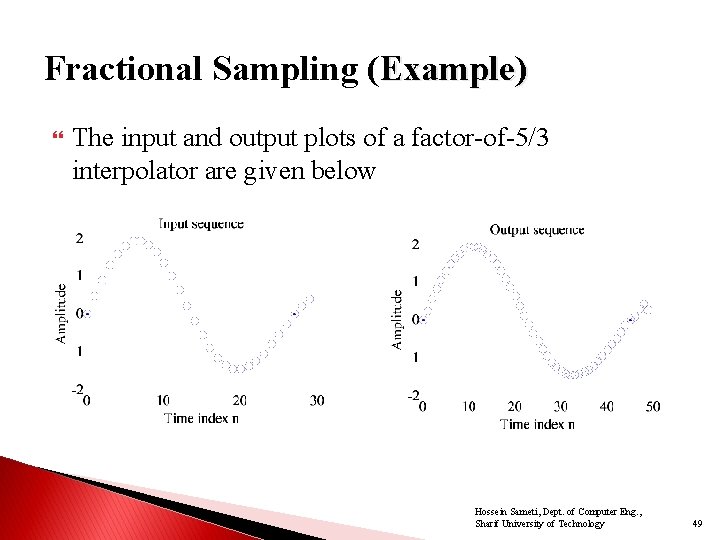
Fractional Sampling (Example) The input and output plots of a factor-of-5/3 interpolator are given below Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 49

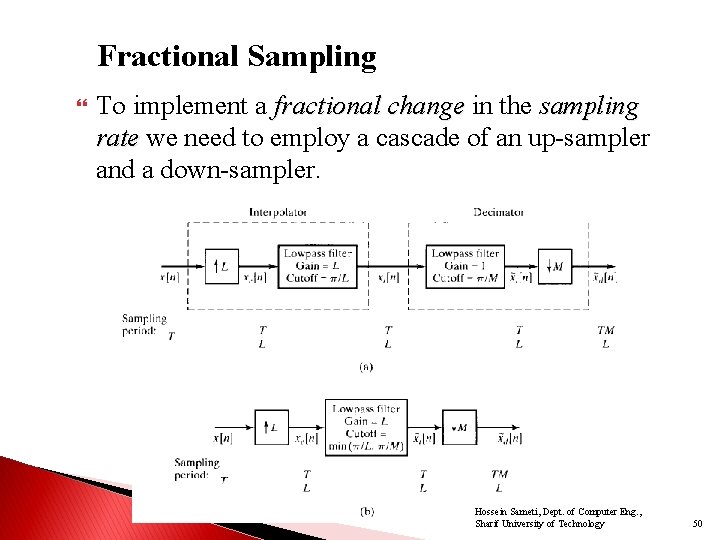
Fractional Sampling To implement a fractional change in the sampling rate we need to employ a cascade of an up-sampler and a down-sampler. Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 50

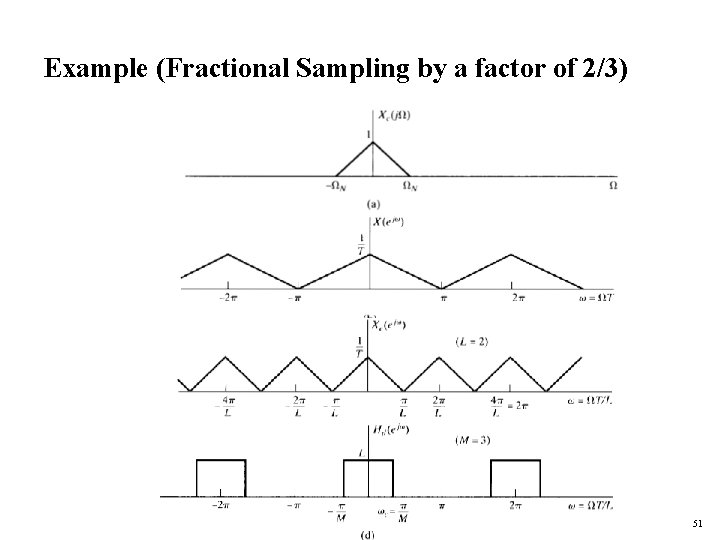
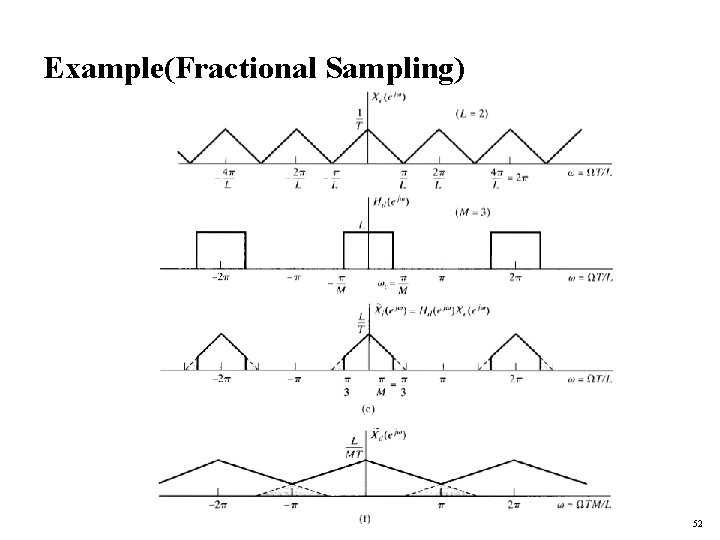
Example (Fractional Sampling by a factor of 2/3) 51

Example(Fractional Sampling) 52

Summary Reviewed sampling of continuous time signals and the relationship between CTFT and DTFT. Derived the effect of downsampling and upsampling of signals in the frequency domain. Adjusting the sampling rate is especially important before applying pattern recognition algorithms, as it can decrease the complexity of the subsequent signal processing algorithms (by decreasing the length of the signal of interest). Hossein Sameti, Dept. of Computer Eng. , Sharif University of Technology 53