CDROM Chapter 15 Introduction to Nonparametric Statistics Chapter

CD-ROM Chapter 15 Introduction to Nonparametric Statistics

Chapter 15 - Chapter Outcomes After studying the material in this chapter, you should be able to: §Recognize when and how to use the runs test and testing for randomness. §Know when and how to perform a Mann-Whitney U test. §Recognize the situations for which the Wilcoxon signed rank test applies and be able to use it in a decisionmaking context. §Perform nonparametric analysis of variance using the Kruskal-Wallis one-way ANOVA.

Nonparametric Statistics Nonparametric statistical procedures are those statistical methods that do not concern themselves with population distributions and/or parameters.

The Runs Test The runs test is a statistical procedure used to determine whether the pattern of occurrences of two types of observations is determined by a random process.

The Runs Test A run is a succession of occurrences of a certain type preceded and followed by occurrences of the alternate type or by no occurrences at all.

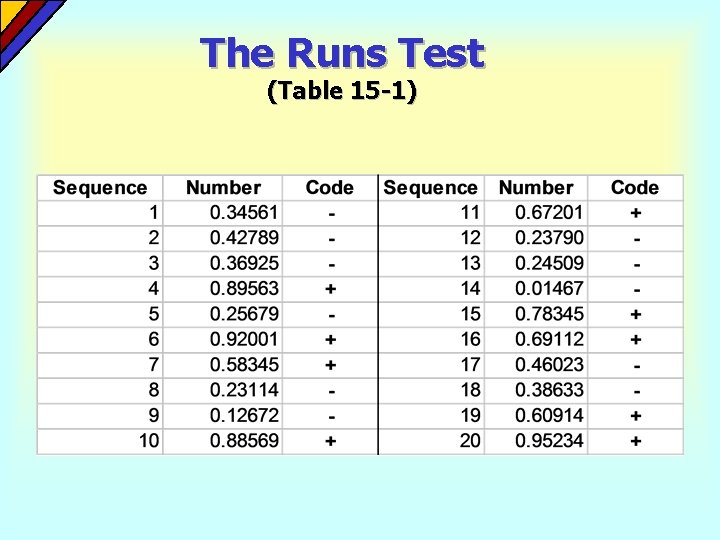
The Runs Test (Table 15 -1)

The Runs Test (Small Sample Example) H 0: Computer-generated numbers are random between 0. 0 and 1. 0. HA: Computer-generated numbers are not random. --- + - ++ --- ++ Runs: 1 2 3 4 5 6 7 8 9 10 There are r = 10 runs From runs table (Appendix K) with n 1 = 9 and n 2 = 11, the critical value of r is 6

The Runs Test (Small Sample Example) Test Statistic: r = 10 runs Critical Values from Runs Table: Possible Runs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Reject H 0 Do not reject H 0 Reject H 0 Decision: Since r = 10, we do not reject the null hypothesis.

Large Sample Runs Test MEAN AND STANDARD DEVIATION FOR r where: n 1 = Number of occurrences of first type n 2 = Number of occurrences of second type

Large Sample Runs Test TEST STATISTIC FOR LARGE SAMPLE RUNS TEST

Large Sample Runs Test (Example 15 -2) Table 15 -2 OOOUOOUOUUOOOOUUOUUOOO UUUOOOOUUUOUUOOUUUUU OOOUOUUOOOOUUUOUUOOOU OOUUOUOOUUUOUUOOOOUUUOOO n 1 = 53 “O’s” n 2 = 47 “U’s” r = 45 runs

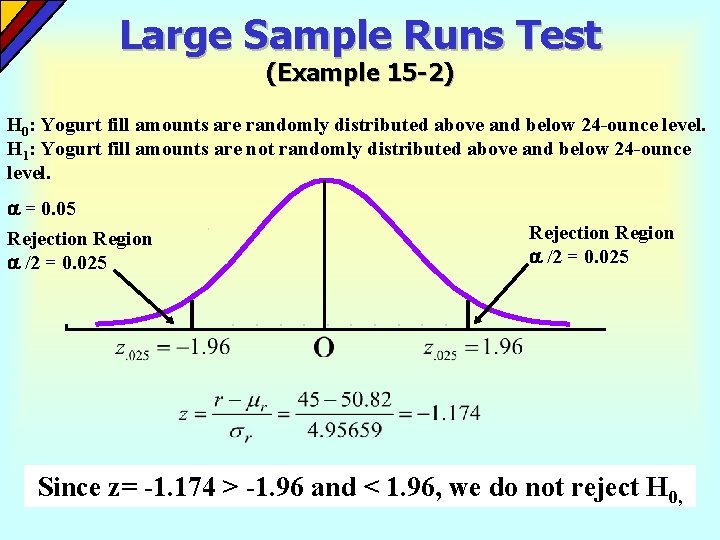
Large Sample Runs Test (Example 15 -2) H 0: Yogurt fill amounts are randomly distributed above and below 24 -ounce level. H 1: Yogurt fill amounts are not randomly distributed above and below 24 -ounce level. = 0. 05 Rejection Region /2 = 0. 025 Since z= -1. 174 > -1. 96 and < 1. 96, we do not reject H 0,

Mann-Whitney U Test The Mann Whitney U test can be used to compare two samples from two populations if the following assumptions are satisfied: • The two samples are independent and random. • The value measured is a continuous variable. • The measurement scale used is at least ordinal. • If they differ, the distributions of the two populations will differ only with respect to the central location.

Mann-Whitney U Test U-STATISTICS where: n 1 and n 2 are the two sample sizes R 1 and R 2 = Sum of ranks for samples 1 and 2

Mann-Whitney U Test - Large Samples - MEAN AND STANDARD DEVIATION FOR THE U-STATISTIC where: n 1 and n 2 = Sample sizes from populations 1 and 2

Mann-Whitney U Test - Large Samples - MANN-WHITNEY U-TEST STATISTIC

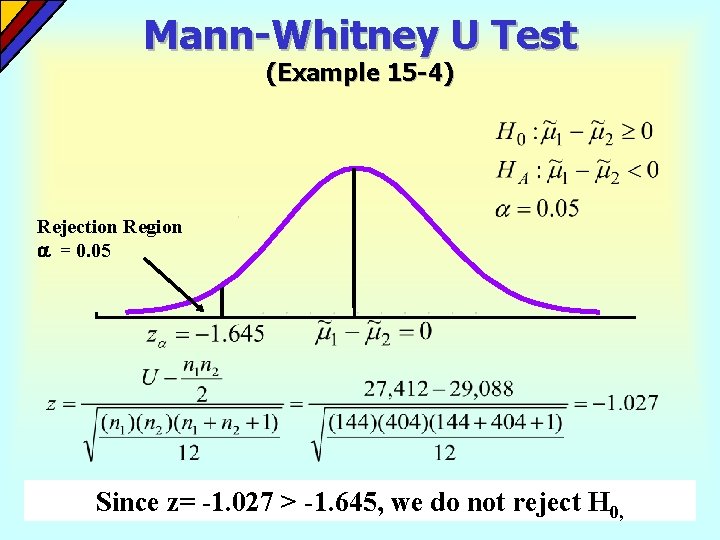
Mann-Whitney U Test (Example 15 -4) Rejection Region = 0. 05 Since z= -1. 027 > -1. 645, we do not reject H 0,

Wilcoxon Matched-Pairs Test The Wilcoxon matched pairs signed rank test can be used in those cases where the following assumptions are satisfied: • The differences are measured on a continuous variable. • The measurement scale used is at least interval. • The distribution of the population differences is symmetric about their median.

Wilcoxon Matched-Pairs Test WILCOXON MEAN AND STANDARD DEVIATION where: n = Number of paired values

Wilcoxon Matched-Pairs Test WILCOXON TEST STATISTIC

Kruskal-Wallis One-Way Analysis of Variance Kruskal-Wallis one-way analysis of variance can be used in one-way analysis of variance if the variables satisfy the following: • They have a continuous distribution. • The data are at least ordinal. • The samples are independent. • The samples come from populations whose only possible difference is that at least one may have a different central location than the others.

Kruskal-Wallis One-Way Analysis of Variance H-STATISTIC where: N = Sum of sample sizes in all samples k = Number of samples Ri = Sum of ranks in the ith sample ni = Size of the ith sample

Kruskal-Wallis One-Way Analysis of Variance CORRECTION FOR TIED RANKINGS where: g = Number of different groups of ties ti = Number of tied observations in the ith tied group of scores N = Total number of observations

Kruskal-Wallis One-Way Analysis of Variance H-STATISTIC CORRECTED FOR TIED RANKINGS

Key Terms • Kruskal-Wallis One. Way Analysis of Variance • Mann-Whitney U Test • Nonparametric Statistical Procedure • Runs Test • Wilcoxon Test