CCS 590 Advanced Algorithms and Complexity 14 NPCompleteness

CCS 590 Advanced Algorithms and Complexity 14. NP-Completeness Chapter 17 x 1 x 2 12 11 x 3 22 13 21 x 4 32 23 31 33 Prof. Abdullah Zawawi Talib, Ph. D. School of Computer Sciences Universiti Sains Malaysia NP-Completeness 1

Outline and Reading P and NP (§ 17. 1) n n n Decision Problems The Complexity Class P The Complexity Class NP An Interesting Problem: VERTEX-COVER Some Thoughts About P and NP NP-completeness (§ 17. 2) n n Definition of NP-hard and NP-complete Polynomial-Time Reducibility and NP-Hardness Some NP-complete problems (§ 17. 4 -17. 6) n n Vertex Cover and Clique Some other NP-complete problems NP-Completeness 2

P and NP The formal notion of “efficient” = that a problem has an algorithm running in time proportional to a polynomial function of its input size, n. “efficient, ” if it runs in time O(nk) on any input of size n, for some constant k > 0. Showing that a problem is NP-complete is admittedly not the same as proving that an efficient algorithm for the problem is impossible, it is nevertheless a powerful statement. NP-Completeness 3

P and NP Basically, showing a problem L is NP -complete means that, although we have been unable to find an efficient algorithm for L, neither has any computer scientist who has ever lived! Indeed, most computer scientists strongly believe it is impossible to solve any NP -complete problem in polynomial time. We need to formally define the class NP and its related class P, and show to prove that some problems are NP -complete. NP-Completeness 4

Decision Problems To simplify our discussion, we restrict our attention to decision problems, i. e. , problems for which the intended output is either “yes” or “no” or 0 or 1. Examples: n Given a string T and a string P, does P appear as a substring of T? n Given two sets S and T, do S and T contain the same set of elements? n Given a graph G with integer weights on its edges, and an integer k, does G have a minimum spanning tree of weight at most k? NP-Completeness 5

Decision Problems The above last problem is an optimization problem where we are trying to minimize or maximize some value. We can often turn an optimization problem into a decision problem. We can introduce a parameter k and ask if the optimal value for the optimization problem is at most or at least k. Note that if we can show that a decision problem is hard, then its related optimization version must also be hard. NP-Completeness 6

The Complexity Class P The complexity class P is the set of all decision problems L that can be decided in worst-case polynomial time. That is, there is an algorithm A that, on input x, runs in p(n) time, where n is the size of x and p(n) is a polynomial, and, if x ∈ L, then A outputs “yes, ” and otherwise A outputs “no. ” NP-Completeness 7

The Complexity Class NP The complexity class NP is defined to include the complexity class P but allow for the inclusion of problems that may not be in P. Specifically, with NP problems, we allow algorithms to perform an additional operation: n choose(b): this operation chooses in a nondeterministic way a bit (that is, a value that is either 0 or 1) and assigns it to b. When an algorithm A uses the choose primitive operation, then we say A is nondeterministic. We state that A nondeterministically accepts an input x if there exists a set of outcomes to the choose calls that A could make on input x such that A would ultimately output “yes. ” NP-Completeness 8

The Complexity Class NP The complexity class NP is the set of every decision problem, L, that can be nondeterministically accepted in polynomial time, where we define the running time, p(n), to be the maximum running time for A taken over all possible outcomes to its choose calls. That is, L is in NP if there is a nondeterministic algorithm A and polynomial p(n) such that, on an input x of size n, if x ∈ L, then there is a set of outcomes to the choose calls in A so that it outputs “yes” and A runs in p(n) time. If x is not in L, then every possible outcome to the choose calls in A results in A outputting “no. ” NP-Completeness 9

NP example Problem: Decide if a graph has an MST of weight K Algorithm: 1. Non-deterministically choose a set T of n-1 edges 2. Test that T forms a spanning tree 3. Test that T has weight at most K Analysis: Testing takes O(n+m) time, so this algorithm runs in polynomial time. NP-Completeness 10

An Interesting Problem: VERTEX-COVER v Network monitoring problem. Suppose we are given a computer network (modelled using a graph G). We would like to monitor all of these connections by installing special monitoring devices on some of the computers, where a monitoring device placed on a computer can continuously check if all the network connections to that computer are working correctly. v But these devices are relatively expensive, so we would like to minimize the number of such devices that we need to deploy. NP-Completeness 11

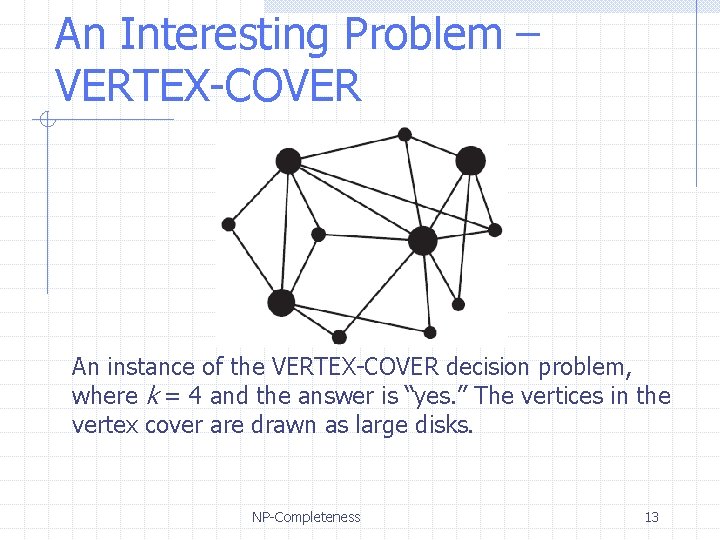
An Interesting Problem – VERTEX-COVER v Viewed as a decision problem, known as VERTEX-COVER, given a graph G and an integer k, and we are asked whethere is a subset C of k vertices such that, for every edge (v, w) of G, v ∈ C or w ∈ C (possibly both). C is known as a vertex cover. v In other words, VERTEX-COVER is the decision problem that takes a graph G and an integer k as input, and asks whethere is a vertex cover for G containing at most k vertices. NP-Completeness 12

An Interesting Problem – VERTEX-COVER An instance of the VERTEX-COVER decision problem, where k = 4 and the answer is “yes. ” The vertices in the vertex cover are drawn as large disks. NP-Completeness 13

An Interesting Problem – VERTEX-COVER Lemma: VERTEX-COVER is in NP. Proof: Given an integer k and a graph G, with its vertices numbered 1 to N. We use repeated calls to the choose method to form a collection C of k numbers that range from 1 to N. As a verification, we insert all the numbers of C into a dictionary, and then we examine each of the edges in G to make sure that, for each edge (v, w) in G, v is in C or w is in C. If we ever find an edge with neither of its end-vertices in G, then we output “no. ” If we run through all the edges of G so that each has an end-vertex in C, then we output “yes. ” NP-Completeness 14

An Interesting Problem – VERTEX-COVER v Such a computation clearly runs in polynomial time. v Note that if G has a vertex cover of size at most k, then there is an assignment of numbers to define the collection C so that each edge of G passes our test and our algorithm outputs “yes. ” v Likewise, if our algorithm outputs “yes, ” then there must be a subset C of the vertices of size at most k, such that C is a vertex cover. v Thus, VERTEX-COVER is in NP. NP-Completeness 15

Polynomial-Time Reducibility and NP-Hardness L, defining some decision problem, is polynomialtime reducible to M, if there is a function f computable in polynomial time, that takes an input x to L, and transforms it to an input f(x) of M, such that x ∈ L if and only if f(x) ∈ M. Shorthand notation: L −poly→ M signifies that L is polynomial-time reducible to M. M is NP-hard, if, for every L ∈ NP, L −poly→ M. If M is NP -hard and also in the class NP itself, then M is NP-complete (one of the hardest problems in NP). NP-Completeness 16

Some Thoughts about P and NP NP-complete problems live here NP P VERTEX COVER Belief: P is a proper subset of NP. Implication: the NP-complete problems are the hardest in NP. Why: Because if we could solve an NP-complete problem in polynomial time, we could solve every problem in NP in polynomial time. That is, if an NP-complete problem is solvable in polynomial time, then P=NP. Since so many people have attempted without success to find polynomial-time solutions to NP-complete problems, showing your problem is NP-complete is equivalent to showing that a lot of smart people have worked on your problem and found no polynomial-time algorithm. NP-Completeness 17

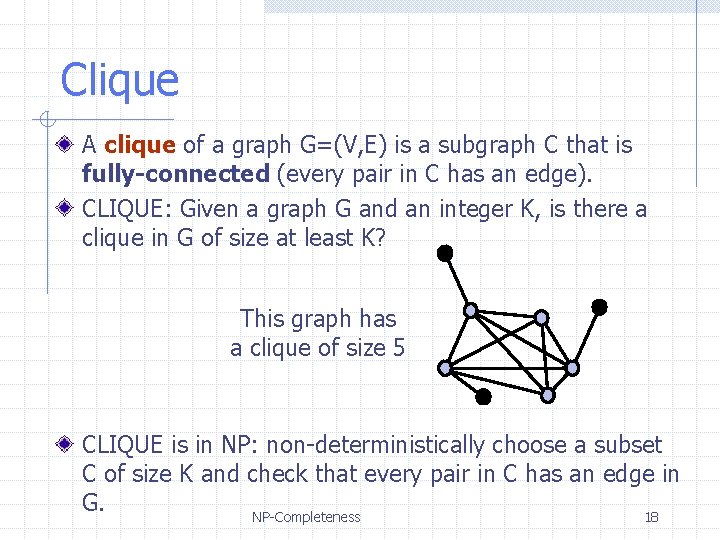
Clique A clique of a graph G=(V, E) is a subgraph C that is fully-connected (every pair in C has an edge). CLIQUE: Given a graph G and an integer K, is there a clique in G of size at least K? This graph has a clique of size 5 CLIQUE is in NP: non-deterministically choose a subset C of size K and check that every pair in C has an edge in G. NP-Completeness 18

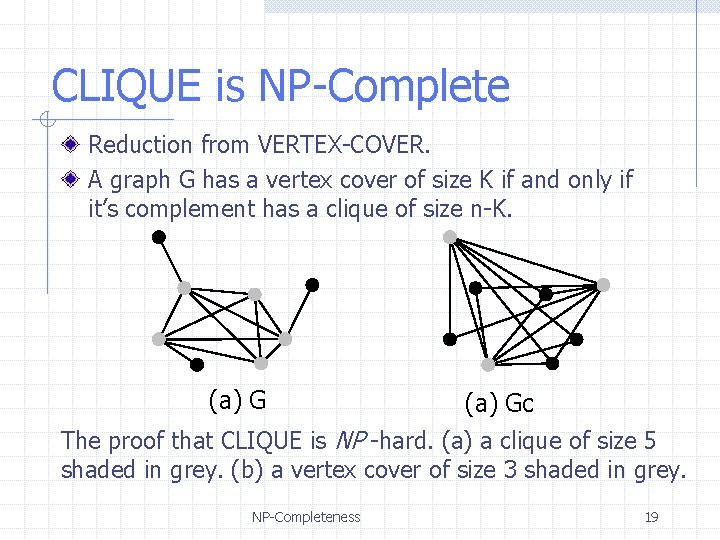
CLIQUE is NP-Complete Reduction from VERTEX-COVER. A graph G has a vertex cover of size K if and only if it’s complement has a clique of size n-K. (a) Gc The proof that CLIQUE is NP -hard. (a) a clique of size 5 shaded in grey. (b) a vertex cover of size 3 shaded in grey. NP-Completeness 19

Some Other -Complete Problems NP SET-COVER: Given a collection of m sets, are there K of these sets whose union is the same as the whole collection of m sets? n NP-complete by reduction from VERTEX-COVER SUBSET-SUM: Given a set of integers and a distinguished integer K, is there a subset of the integers that sums to K? n NP-complete by reduction from VERTEX-COVER NP-Completeness 20

Some Other -Complete Problems NP 0/1 Knapsack: Given a collection of items with weights and benefits, is there a subset of weight at most W and benefit at least K? n NP-complete by reduction from SUBSET-SUM Hamiltonian-Cycle: Given an graph G, is there a cycle in G that visits each vertex exactly once? n NP-complete by reduction from VERTEX-COVER Traveling Saleperson Tour: Given a complete weighted graph G, is there a cycle that visits each vertex and has total cost at most K? n NP-complete by reduction from Hamiltonian-Cycle. NP-Completeness 21