Cavity quantum electrodynamics for superconducting electrical circuits An

Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computing Student Presentation Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 1

Presentation Overview § Introduction to Theory § § Atom in Cavity (Jaynes-Cummings-Hamiltonian) Energy Levels and Energy Levels Splitting Decay Channels Cases: Zero and Strong Detuning § Introduction to Circuit § Components of Circuit § Analogue of Atom in Cavity and TL CPB system § Readout in dispersive regime Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 2

Revision: Jaynes-Cummings Hamiltonian § Hamiltonian of a two-level atom interacting with a photon in a cavity Martin Butterschön & Leandro von Werra Martin Buttenschön & Leandro von Werra | 1. 12. 2014 15. 04. 2016 | 3

Revision: Jaynes-Cummings Hamiltonian, Interaction Term Dipole Moment: Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 4

Revision: Jaynes-Cummings Hamiltonian, Interaction Term Jaynes-Cummings Hamiltonian Martin Butterschön & Leandro von Werra Martin Buttenschön & Leandro von Werra | 1. 12. 2014 15. 04. 2016 | 5

Eigenstates Case : Martin Butterschön & Leandro von Werra Martin Buttenschön & Leandro von Werra | 1. 12. 2014 15. 04. 2016 | 6

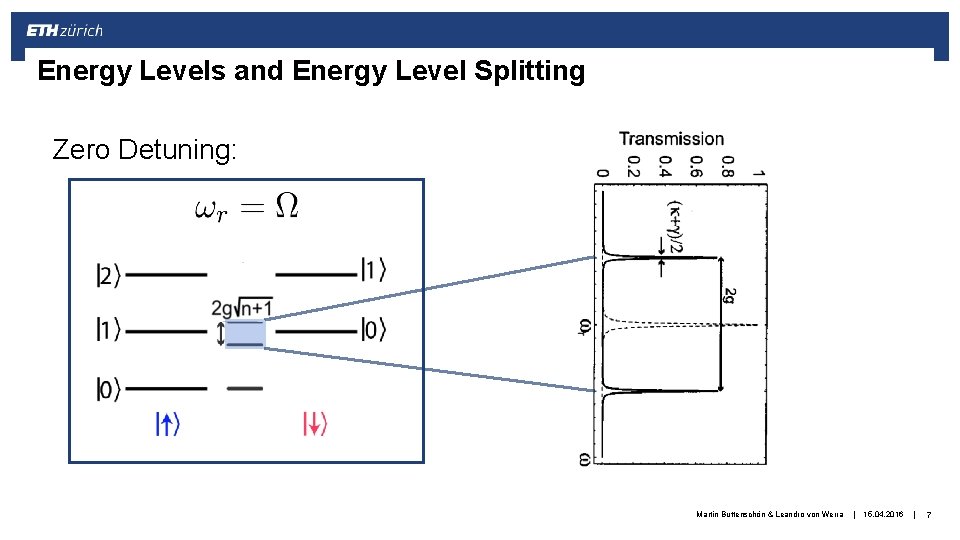
Energy Levels and Energy Level Splitting Zero Detuning: Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 7

Eigenstates Case : Martin Butterschön & Leandro von Werra Martin Buttenschön & Leandro von Werra | 1. 12. 2014 15. 04. 2016 | 8

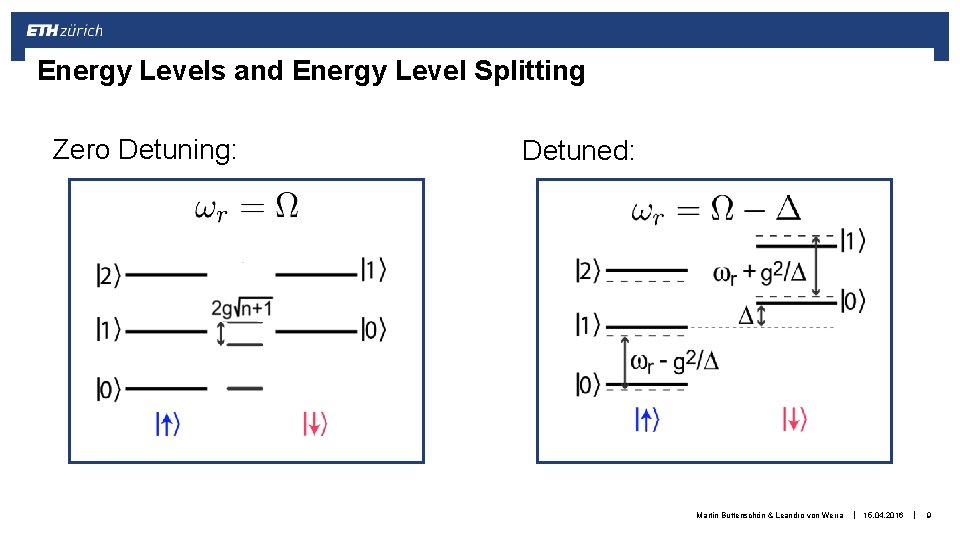
Energy Levels and Energy Level Splitting Zero Detuning: Detuned: xx Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 9

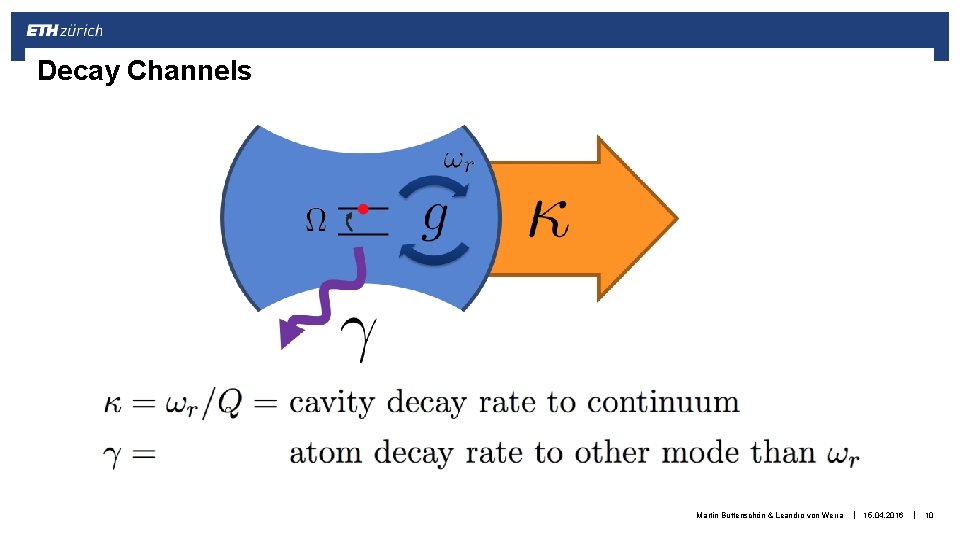
Decay Channels Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 10

Decay Terms in the Hamiltonian Strong coupling Make as big and as small as possible! Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 11

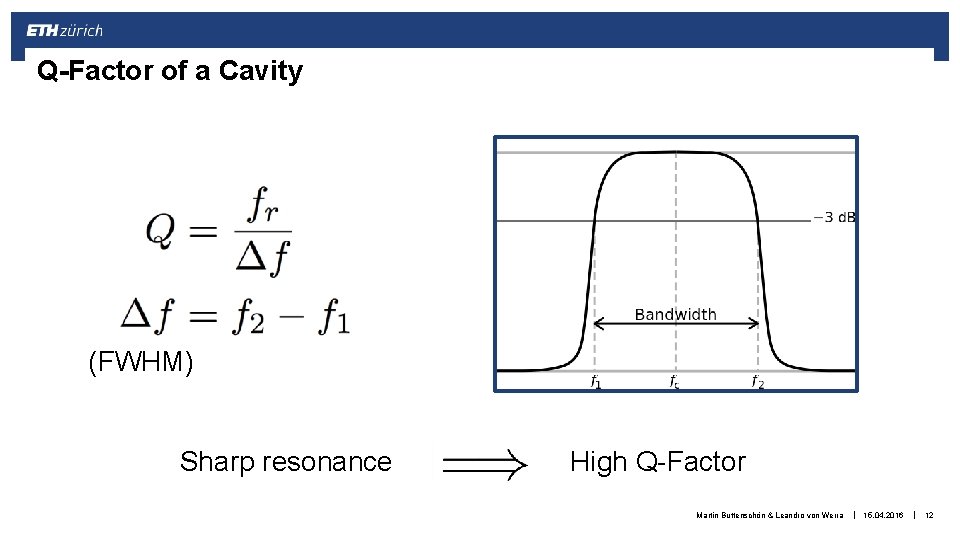
Q-Factor of a Cavity (FWHM) Sharp resonance High Q-Factor Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 12

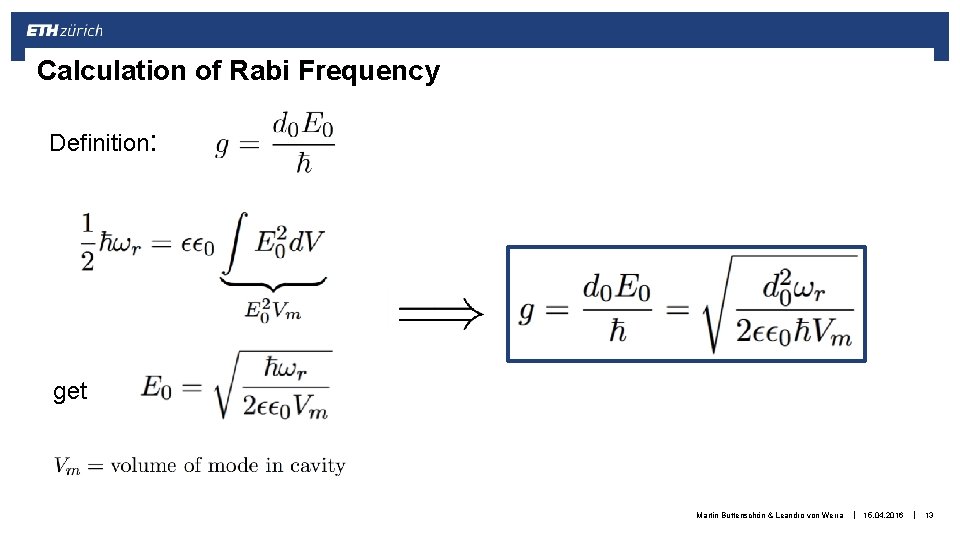
Calculation of Rabi Frequency Definition: get Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 13

Presentation Overview § Introduction to Theory § § Atom in Cavity (Jaynes-Cummings-Hamiltonian) Energy Levels and Energy Levels Splitting Decay Channels Cases: Zero and Strong Detuning § Introduction to Circuit § Components of Circuit § Analogue of Atom in Cavity and TL CPB system § Readout in dispersive regime Martin Buttenschön & Leandro von Werra Martin Butterschön & Leandro von Werra | 15. 04. 2016 1. 12. 2014 | 14

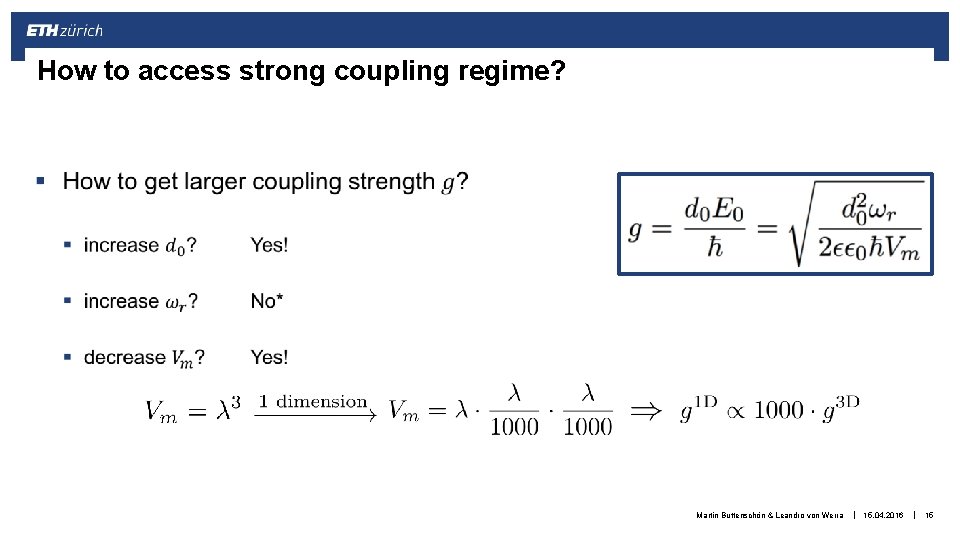
How to access strong coupling regime? § Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 15

For comparable 3 D vs 1 D system, 1 D has greater coupling Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 16

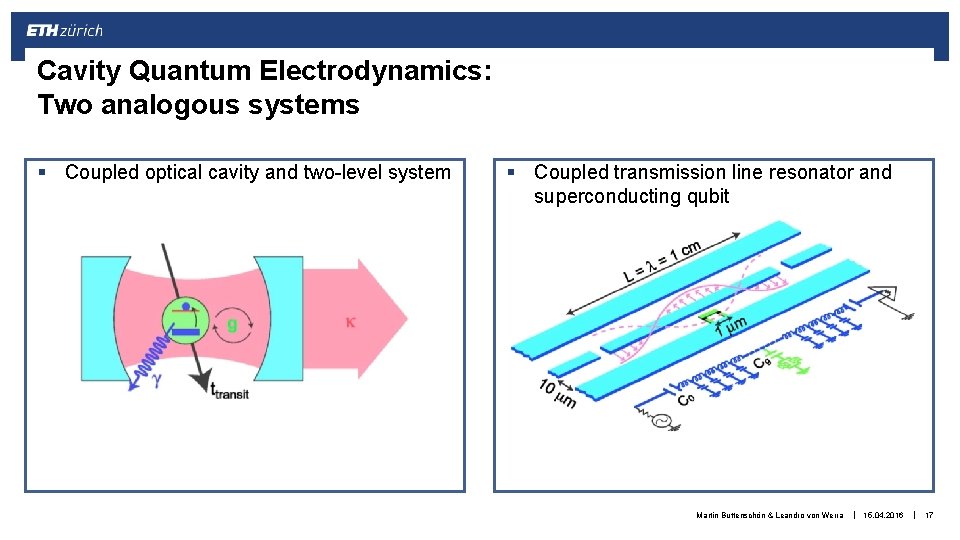
Cavity Quantum Electrodynamics: Two analogous systems § Coupled optical cavity and two-level system § Coupled transmission line resonator and superconducting qubit Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 17

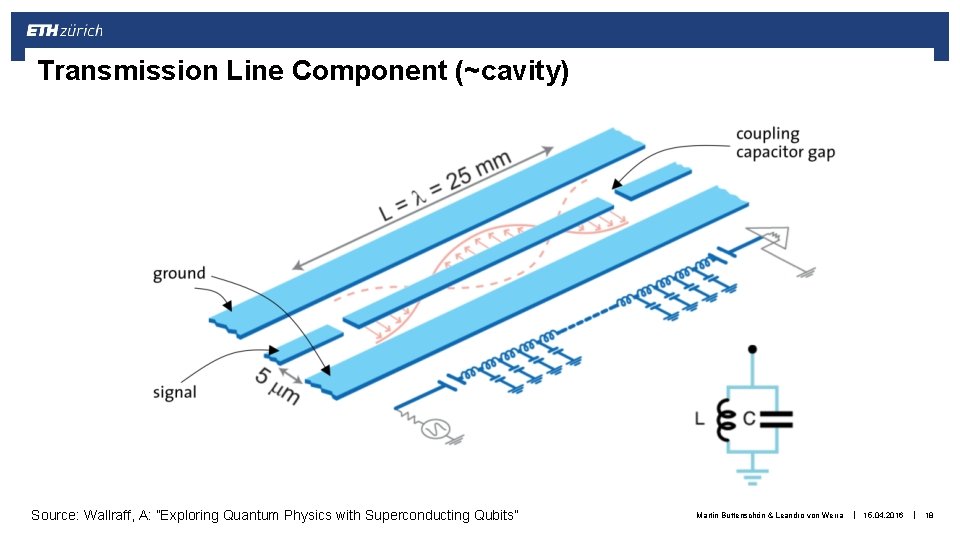
Transmission Line Component (~cavity) Source: Wallraff, A: ”Exploring Quantum Physics with Superconducting Qubits” Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 18

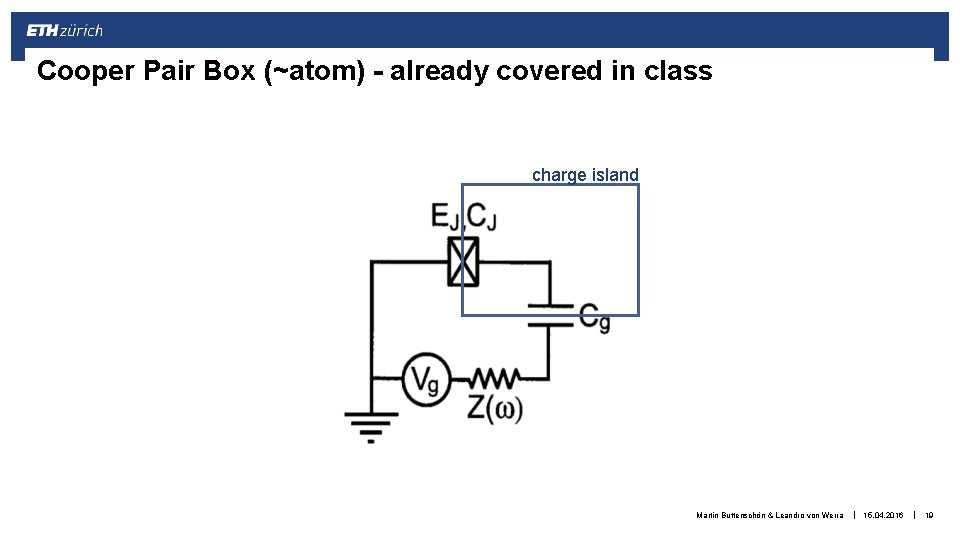
Cooper Pair Box (~atom) - already covered in class charge island Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 19

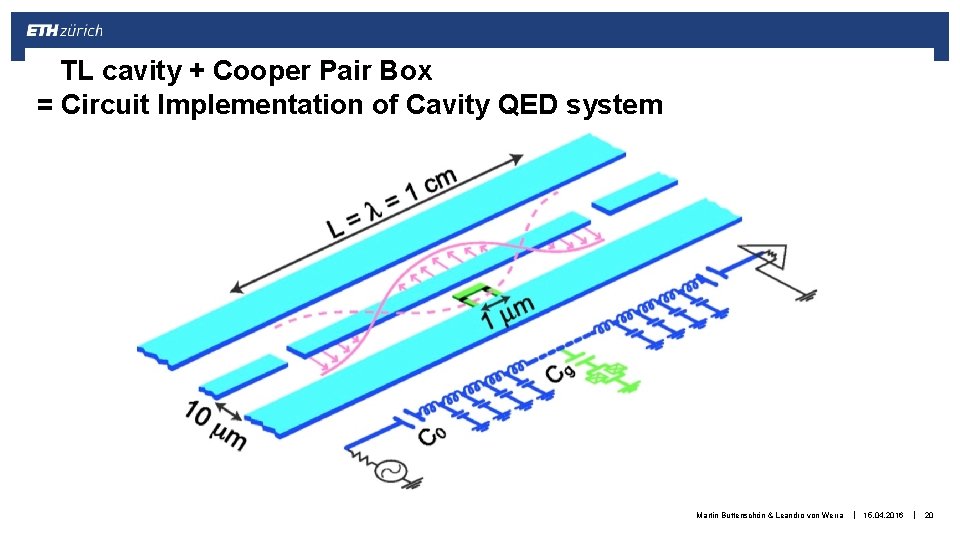
TL cavity + Cooper Pair Box = Circuit Implementation of Cavity QED system Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 20

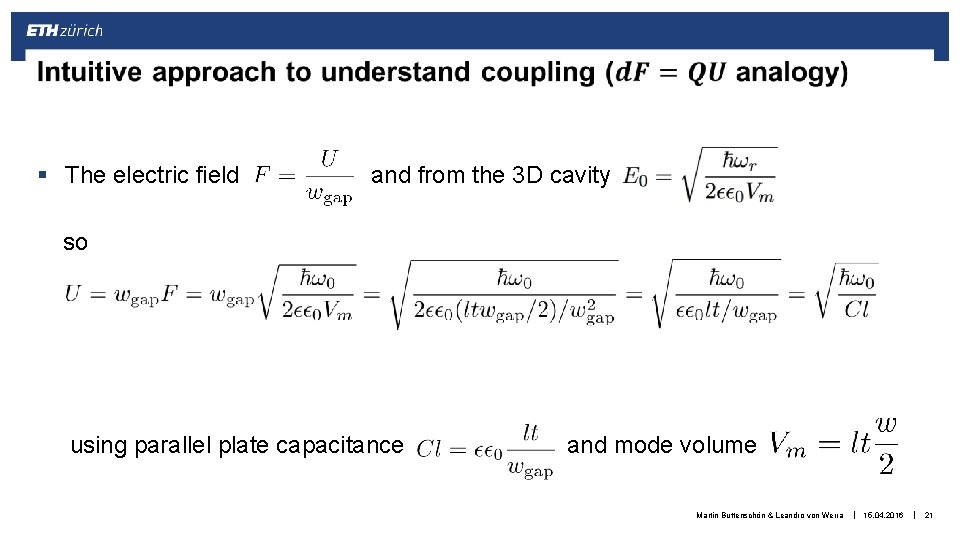
§ The electric field and from the 3 D cavity so using parallel plate capacitance and mode volume Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 21

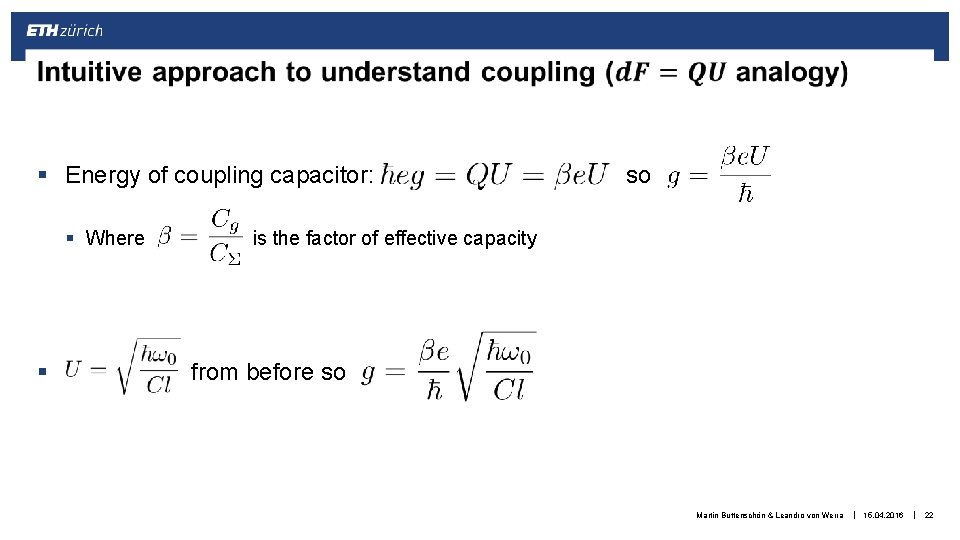
§ Energy of coupling capacitor: § Where so is the factor of effective capacity § from before so Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 22

Wrap-up: What did I show you so far? § Two equivalent systems § The same physical understanding applies to both Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 23

§ Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 24

There are many other implementations of CQED: So why is this system so popular? § Small effective volume § On-chip realization § (with existing lithographic technology) § Strongly suppressed spontaneous emission § (also true for Rydberg atoms or 3 D cavities) § Very large Rabi frequency § Coupling remains constant § (as qubit remains fixed in positions) § Easy read-out Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 25

Sources § Blais, A; Huang R; Wallraff, A; Girvin SM; and RJ Schoelkopf: ”Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation”. Physical Review A 69 (2004). § Thiele, T: ”Coherent manipulation of Rydberg atoms close to surfaces at cryogenic temperatures”. 2016. Unpublished doctoral dissertation. ETH Zürich. § Walter, T: ”Introduction to Quantum Information Science”. 2016. Lecture Notes for QSIT taught by Andreas Wallraff. ETH Zürich. Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 26

Thanks to Tobias on guiding and coaching us Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 27

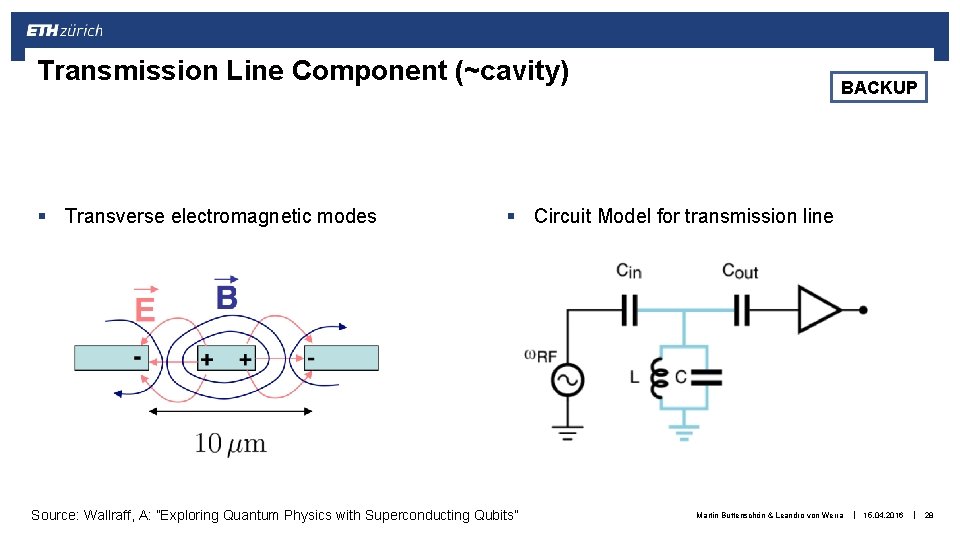
Transmission Line Component (~cavity) § Transverse electromagnetic modes BACKUP § Circuit Model for transmission line Source: Wallraff, A: ”Exploring Quantum Physics with Superconducting Qubits” Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 28

To the QED system BACKUP complete CPB Hamiltonian in Number basis Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 29

BACKUP Hamiltonian for dispersive regime is equivalently Martin Buttenschön & Leandro von Werra | 15. 04. 2016 | 30