Causal Forecasting by Gordon Lloyd What will be

Causal Forecasting by Gordon Lloyd

What will be covered? What is forecasting? n Methods of forecasting n What is Causal Forecasting? n When is Causal Forecasting Used? n Methods of Causal Forecasting n Example of Causal Forecasting n

What is Forecasting? n Forecasting is a process of estimating the unknown

Business Applications n Basis for most planning decisions – – – – Scheduling Inventory Production Facility Layout Workforce Distribution Purchasing Sales

Methods of Forecasting n Time Series Methods n Causal Forecasting Methods n Qualitative Methods

What is Causal Forecasting? n Causal forecasting methods are based on the relationship between the variable to be forecasted an independent variable.

When Is Causal Forecasting Used? Know or believe something caused demand to act a certain way n Demand or sales patterns that vary drastically with planned or unplanned events n

Types of Causal Forecasting Regression n Econometric models n Input-Output Models: n

Regression Analysis Modeling n Pros – Increased accuracies – Reliability – Look at multiple factors of demand n Cons – Difficult to interpret – Complicated math

Linear Regression Line Formula y = a + bx y = the dependent variable a = the intercept b = the slope of the line x = the independent variable

Linear Regression Formulas a = Y – b. X b = ∑xy – n. XY ∑x² - n. X² a = intercept b = slope of the line X = ∑x = mean of x n the x data Y = ∑y = mean of y n the y data n = number of periods

Correlation n Measures the strength of the relationship between the dependent and independent variable

Correlation Coefficient Formula r= ______n∑xy - ∑x∑y______ √[n∑x² - (∑x)²][n∑y² - (∑y)²] ___________________ r = correlation coefficient n = number of periods x = the independent variable y = the dependent variable

Coefficient of Determination Another measure of the relationship between the dependant and independent variable n Measures the percentage of variation in the dependent (y) variable that is attributed to the independent (x) variable r = r² n

Example n n Concrete Company Forecasting Concrete Usage – How many yards will poured during the week n Forecasting Inventory – – – n Cement Aggregate Additives Forecasting Work Schedule

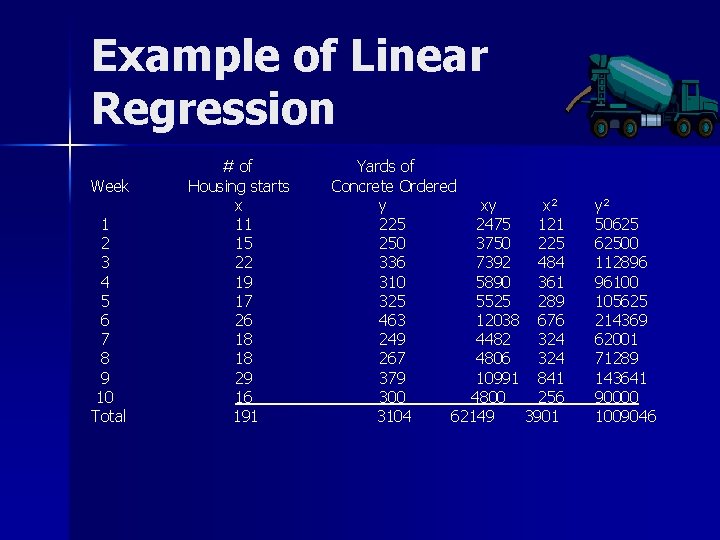
Example of Linear Regression Week 1 2 3 4 5 6 7 8 9 10 Total # of Housing starts x 11 15 22 19 17 26 18 18 29 16 191 Yards of Concrete Ordered y xy x² 225 2475 121 250 3750 225 336 7392 484 310 5890 361 325 5525 289 463 12038 676 249 4482 324 267 4806 324 379 10991 841 300 4800 256 3104 62149 3901 y² 50625 62500 112896 96100 105625 214369 62001 71289 143641 90000 1009046

Example of Linear Regression X = 191/10 = 19. 10 Y = 3104/10 = 310. 40 b = ∑xy – nxy = (62149) – (10)(19. 10)(310. 40) ∑x² -nx² (3901) – (10)(19. 10)² b = 11. 3191 a = Y - b. X = 310. 40 – 11. 3191(19. 10) a = 94. 2052

Example of Linear Regression Equation y = a + bx y = 94. 2052 + 11. 3191(x) Concrete ordered for 25 new housing starts y = 94. 2052 + 11. 3191(25) y = 377 yards

Correlation Coefficient Formula r= ______n∑xy - ∑x∑y______ √[n∑x² - (∑x)²][n∑y² - (∑y)²] ___________________ r = correlation coefficient n = number of periods x = the independent variable y = the dependent variable

Correlation Coefficient r= ______n∑xy - ∑x∑y______ √[n∑x² - (∑x)²][n∑y² - (∑y)²] r= 10(62149) – (191)(3104) √[10(3901)-(3901)²][10(1009046)²] r =. 8433

Coefficient of Determination r =. 8433 r² = (. 8433)² r² =. 7111

Excel Regression Example # of Housing Starts Week 1 2 3 4 5 6 7 8 9 10 x 11 15 22 19 17 26 18 18 29 16 # of Yards of Concrete Ordered y 225 250 336 310 325 463 249 267 379 300

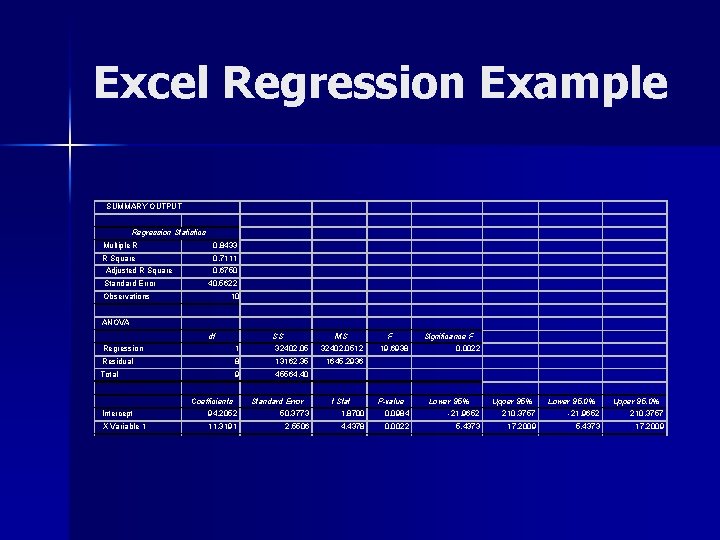
Excel Regression Example SUMMARY OUTPUT Regression Statistics Multiple R 0. 8433 R Square 0. 7111 Adjusted R Square Standard Error 0. 6750 40. 5622 Observations 10 ANOVA df SS MS Regression 1 32402. 0512 Residual 8 13162. 35 1645. 2936 Total 9 45564. 40 Coefficients Standard Error t Stat F 19. 6938 P-value Significance F 0. 0022 Lower 95% Upper 95% Lower 95. 0% Upper 95. 0% Intercept 94. 2052 50. 3773 1. 8700 0. 0984 -21. 9652 210. 3757 X Variable 1 11. 3191 2. 5506 4. 4378 0. 0022 5. 4373 17. 2009

Excel Regression Example SUMMARY OUTPUT Regression Statistics Multiple R R Square Adjusted R Square Standard Error Observations 0. 8433 0. 7111 0. 6750 40. 5622 10 ANOVA df Regression Residual Total Intercept X Variable 1 1 8 9 Coefficients 94. 2052 11. 3191

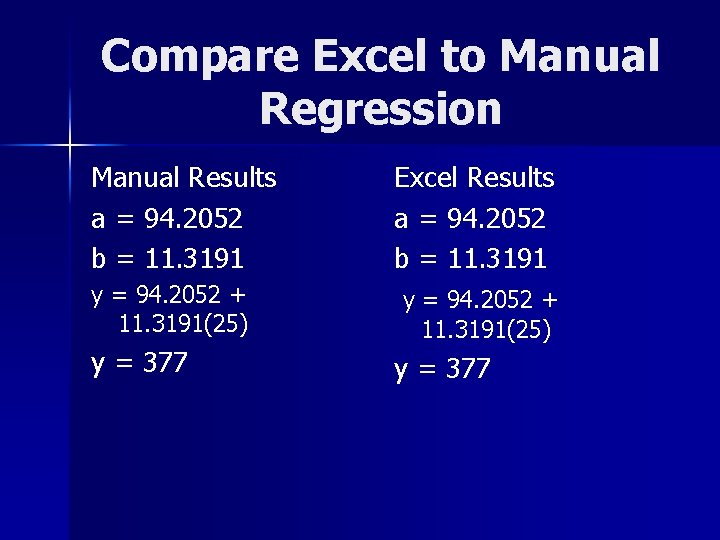
Compare Excel to Manual Regression Manual Results a = 94. 2052 b = 11. 3191 y = 94. 2052 + 11. 3191(25) y = 377 Excel Results a = 94. 2052 b = 11. 3191 y = 94. 2052 + 11. 3191(25) y = 377

Excel Correlation and Coefficient of Determination Regression Statistics Multiple R 0. 8433 R Square 0. 7111

Compare Excel to Manual Regression n Manual Results r =. 8344 r² =. 7111 n Excel Results r =. 8344 r² =. 7111

Conclusion Causal forecasting is accurate and efficient n When strong correlation exists the model is very effective n No forecasting method is 100% effective n

Reading List § Lapide, Larry, New Developments in Business Forecasting, Journal of Business Forecasting Methods & Systems, Summer 99, Vol. 18, Issue 2 http: //morris. wharton. upenn. edu/forecast, § Armstrong, University of Pennsylvania www. uoguelph. ca/~dsparlin/forecast. htm, § Principles of Forecasting, A Handbook for Researchers and Practitioners, Edited by J. Scott Forecasting