Causal Diagrams Directed Acyclic Graphs Greenland Pearl Robins

Causal Diagrams / Directed Acyclic Graphs Greenland, Pearl, Robins (1999) Lecture 2 1

Directed Acyclic Graphs (DAGs) • Provides formal theory for deciding what variables to adjust for • Much of theory comes from Judea Pearl • Related to structural equation models in the social sciences literature but does not require parametric assumptions • Non-parametric: Display relationships but assume no parametric form of those relationships. 2

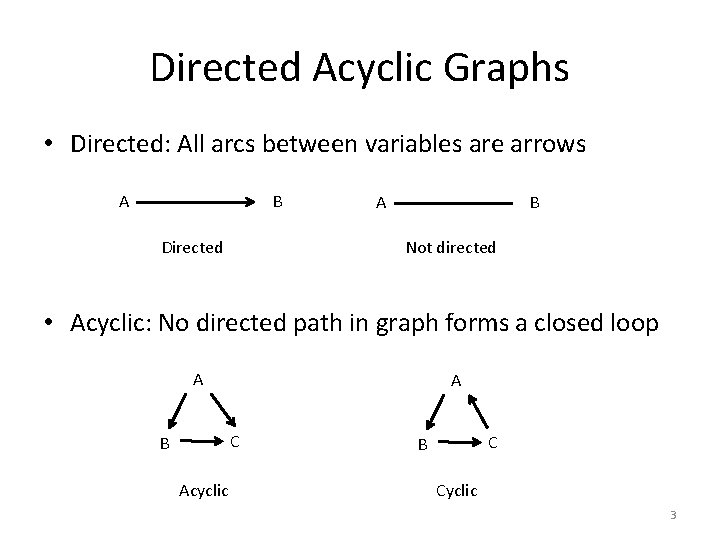
Directed Acyclic Graphs • Directed: All arcs between variables are arrows A B Directed A B Not directed • Acyclic: No directed path in graph forms a closed loop A A C B Acyclic C B Cyclic 3

Confounder • Classical criteria – Variable is a cause of outcome, – Variable is associated with exposure, and – Variable is not an effect of the exposure. C E C D C is a confounder (e. g. , observational study) E D C is not a confounder (e. g. , randomized study) 4

Terminology Nodes/vertices: points in graph representing variables Arc/Edge: any line or arrow connecting two nodes Two nodes are adjacent if they are directly connected by an arc Direct effect: adjacent nodes with single headed arrow. Path: any unbroken route traced out along or against arrows or lines connecting nodes. • Directed (causal) path: path that can be traced through a sequence of singleheaded arrows, always entering an arrow through the tail and leaving through the head. • X is an ancestor or cause of Y if there is a directed path leading out of X into Y. • • • In such a case, Y is a descendant of X or affected by X. • X is said to be a parent of Y in a graph if there is a single-headed arrow from X to Y. • In such a case, Y is a child of X or directly affected by X. • A path that connects X to Y is a backdoor path if it has an arrowhead pointing to X. • A path collides at variable X if the path enters and exits X through arrowheads; X is called a collider. • A path is blocked if it has one or more colliders; otherwise it is unblocked. B A C E D 5

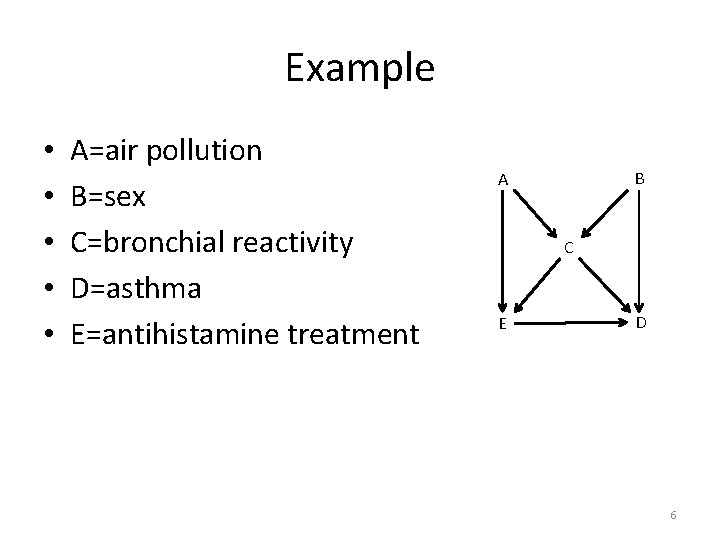
Example • • • A=air pollution B=sex C=bronchial reactivity D=asthma E=antihistamine treatment B A C E D 6

Example • Assuming the graph is correct, what is the smallest subset from the covariates A, B, and C that would be sufficient for adjustment to estimate the effect of E on D without bias? B A C E D 7

Back-door test • Given a DAG and a set S of variables in the graph that are not descendants of E or D, S is sufficient for adjustment if there is no unblocked backdoor path from E to D. • Equivalently: – Every unblocked backdoor path from E to D is intercepted by a variable in S, and – Every unblocked path from E to D induced by adjustment for the variables in S is intercepted by a variable in S. 8

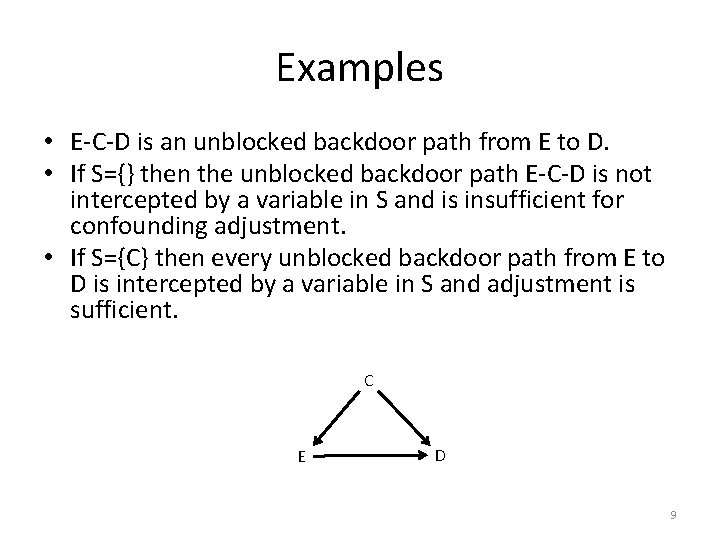
Examples • E-C-D is an unblocked backdoor path from E to D. • If S={} then the unblocked backdoor path E-C-D is not intercepted by a variable in S and is insufficient for confounding adjustment. • If S={C} then every unblocked backdoor path from E to D is intercepted by a variable in S and adjustment is sufficient. C E D 9

Examples • There are no unblocked backdoor path from E to D. • Therefore S={} is sufficient for confounding adjustment. • If S={C} then, there is still no unblocked backdoor path from E to D and adjustment is sufficient. • S={} is minimally sufficient. C E D 10

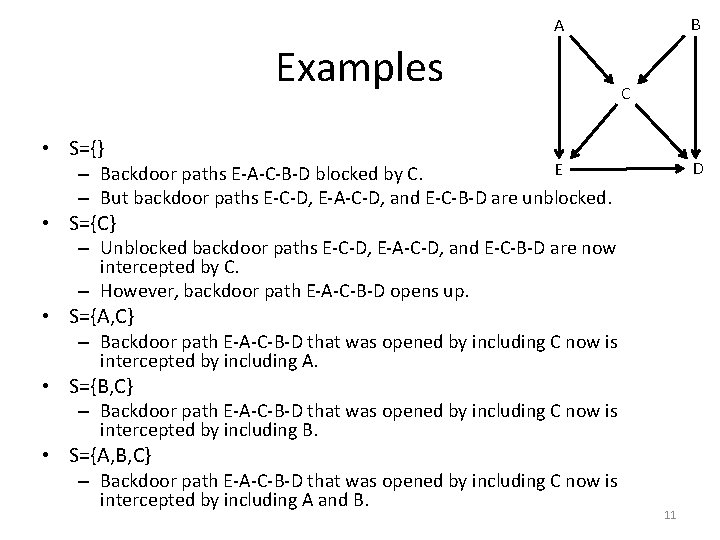
B A Examples C • S={} D E – Backdoor paths E-A-C-B-D blocked by C. – But backdoor paths E-C-D, E-A-C-D, and E-C-B-D are unblocked. • S={C} – Unblocked backdoor paths E-C-D, E-A-C-D, and E-C-B-D are now intercepted by C. – However, backdoor path E-A-C-B-D opens up. • S={A, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including A. • S={B, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including B. • S={A, B, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including A and B. 11

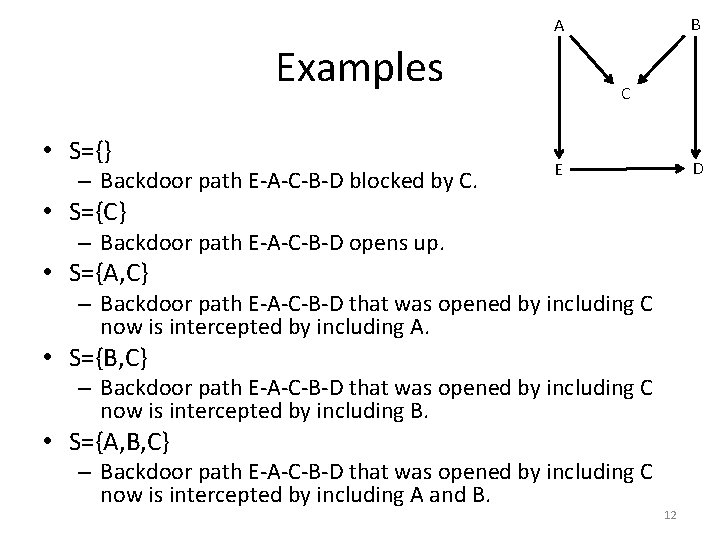
B A Examples • S={} – Backdoor path E-A-C-B-D blocked by C. C D E • S={C} – Backdoor path E-A-C-B-D opens up. • S={A, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including A. • S={B, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including B. • S={A, B, C} – Backdoor path E-A-C-B-D that was opened by including C now is intercepted by including A and B. 12

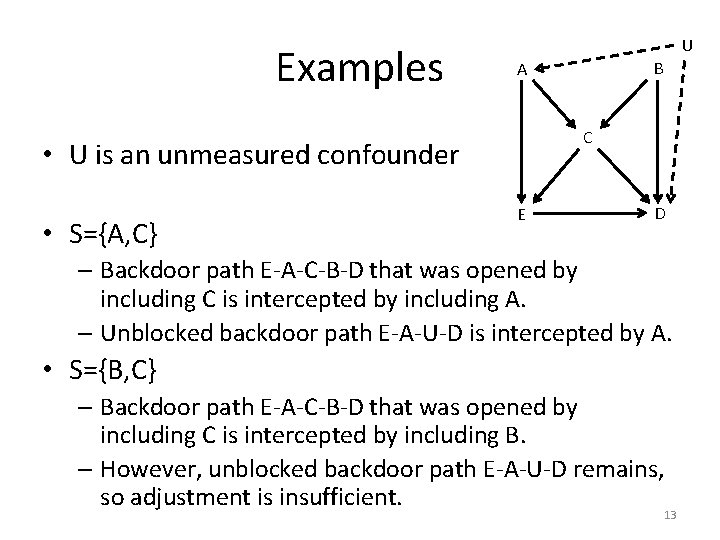
Examples U C • U is an unmeasured confounder • S={A, C} B A E D – Backdoor path E-A-C-B-D that was opened by including C is intercepted by including A. – Unblocked backdoor path E-A-U-D is intercepted by A. • S={B, C} – Backdoor path E-A-C-B-D that was opened by including C is intercepted by including B. – However, unblocked backdoor path E-A-U-D remains, so adjustment is insufficient. 13